Many music theorists believe that the purpose of musical analysis is to explicate the logical, rational organization of musical compositions and to study syntactic relationships present in these works through consideration of the correspondences between structural functions and expressive effect. Through the continuing influence of Heinrich Schenker and his disciples, many theorists also believe that the concept of hierarchic levels in all elements of musical structure (tonality, melody, harmony, texture and rhythm) is germane to the functioning of events within any given context.

The methodologies appropriate to courses dealing with the analysis of form and structure in "tonal" music are presently being reexamined in the light of current analytical philosophies. The prognosis regarding the analysis of medieval and Renaissance music, however, is not as favorable; practically all the analysis of this repertory undertaken at both undergraduate and graduate levels exists as "enrichment" to other established courses, either as part of a traditional tonal form and analysis course or, more customarily, as occasional illustrative side-trips in the period lecture courses given by historians. The methodologies and results vary widely, and are extremely dependent upon the background, interests and analytical point of view of each instructor.

The rationale behind this fragmented, sporadic and arbitrary coverage of the topic cannot be the result of a lack of sufficient interest in the repertory. On the contrary the recent proliferation of university collegia and other performing ensembles demonstrates a rapidly growing interest in early music. Still only a few institutions list pre-tonal analysis courses in their catalogs.

It is my strong belief that as long as treatment of the subject remains parochial and instructor dependent, rigorous and systematic coverage—in a manner analogous to that given to "tonal" music—will seldom take place. Many historians teaching the subject will not be conversant with the powerful analytical concepts being developed through current theoretical research and many teachers of music theory, whether or not they subscribe to Schenker's explication of triadic tonality, seem too steadfastly grounded—both intellectually and aurally—in a triadically-conceived musical reality to be able to deal effectively with another consonant repertory which was not conceptually based upon triad structures.

In this paper, I will describe two basic concepts: modal procedure and the discant idea, which I believe are particularly relevant to the analysis of early music. Neither of these concepts is new or radical. What is progressive, however, is the manner in which I have combined the melodic principles of Gregorian chant theory and the contrapuntal principles of discant theory—both disciplines undoubtedly understood by medieval and Renaissance composers—with the concepts of prolongation, structural levels, and essential voice leading, as first expressed in the theories of Schenker. The methodology which will be described here is, therefore, rather interdisciplinary in its viewpoint as it combines concepts ordinarily investigated and appreciated by musicologists with an analytical philosophy primarily identified with certain music theorists.

When we listen to a "tonal" composition our aural reactions to it are filtered largely through an elaborate set of assumptions and expectations conditioned by our previous experiences with similar pieces. As each of us was reared in the twentieth century and exposed mainly to western music—in our early years at least—our notions of "tonality" are grounded in the musical repertories of the eighteenth and nineteenth centuries. That is to say a combination of nursery songs, elementary instrumental etudes, radio and television commercial music, as well as the traditional art music repertory has so shaped our aural set that, for example, our appreciation of the dominant-tonic relationship is almost instinctive.

Let us consider for a moment the aural background of the fifteenth-century musician. Historians tell us that many of them received their early training as choirboys; indeed, we don't know exactly when Dufay and Josquin were born. Our first knowledge of their existence comes from the attendance rolls at choir schools at Cambrai and St. Quentin. As choirboys their daily musical fare was drawn from that enormous corpus of liturgical melodies, the Gregorian chant repertory. Fifteenth-century children presumably had their own nursery songs but that secular monophonic repertory was probably not substantially different, tonally-speaking, from plainchant.

The point I'm trying to make should be blatantly obvious—that the Renaissance musician's aural perceptions of tonal structure were rooted in the normative tonal relationships which obtained in the plainchant repertory to which he was exposed practically from birth. And if we, as twentieth-century music theorists, accept the validity of that assumption, then we should also appreciate the value if not the necessity of relating tonal structure in Renaissance music to the syntax of plainchant.¹

Medieval and early Renaissance modal theory distinguished four pairs of modes, each composed of a distinct species of fourth and fifth, joined conjunctly by a common pitch. In the authentic members of each pair, or maneria, the fifth is placed below the fourth; the finalis is the lower pitch of the fifth and the cofinalis is the upper pitch. In the plagal members of each pair, the fifth is placed above the fourth; the finalis, therefore, is the common pitch between the species of fourth and fifth, and the cofinalis is the lower pitch of the fourth. We must remember, however, that the concept of mode was originally intended to simplify the classification of chant and the essential characteristic of each mode was its species of fourth and fifth. It was only with Alia Musica, an important late ninth-century collection of treatises, that the idea of mode as scale began to appear.² A particular chant's melodic motion is always directed toward the definition of a modal range by the elaboration of its characteristic species of fourth and fifth. The finalis and cofinalis, the tones of conjunction between the characteristic species, naturally assume structural weight as points of pivot and repose, establishing melodic goals.

In addition to the modal skeleton of the characteristic interval species, the syntax of a particular mode derived from other factors as well. Each mode possessed its own repertory of recurring melodic formulae; within these one notes the practical and structural significance of certain other pitches around the finalis and cofinalis, such as the particular scale degrees used to begin or close melodic distinctions, and the various reciting tones and differentiae. Thus the tonal structure of a given mode may be seen to derive not only from its finalis, its interval species and its ambitus (standard range), but also—and perhaps even more significantly—from its recurring melodic formulae and the functional relationships among its other structural pitches.

Renaissance theorists dealt with the structural pitches common to each mode quite systemically. Tinctoris,³ Aaron,⁴ and Gafurius,⁵ to name but three, each discussed particular pitches appropriate to the beginnings and endings of phrases. Aaron even distinguished between pitches suitable to the upper structural voice and the lower structural voice.⁶ Most of these inventories are essentially identical, and indicate the presence of a well-developed sense of tonal relationships within the system of the four modes.

I will give a few examples. In the Phrygrian maneria, theorists sanctioned as structural pitches the differential endings on the third and fourth degrees, and on the subtonium modi (the step below the finalis), but also mentioned the sixth degree (which is a reciting tone in the authentic member of the modal pair). These abstractions are strongly evident in the music itself; for example, Josquin used the fourth degree in this mode in a manner analogous to his treatment of the cofinalis in the Dorian maneria on E but, instead, wrote many pieces in a tonality which, on the surface, seems quite similar to C major, while employing Phrygian interval species and structural pitch relationships. This observation is not as problematic as it may seem at first, for many medieval chants classified in the Phrygian maneria prolong the reciting tone c and the differentia termination G more than they prolong the finalis E.⁷ To our ears, such pieces seem to slide effortlessly between C major and E Phrygian.

Example 1, In convertendo, illustrates this point.

 

Ex. l. This is the versus, In convertendo, of the gradual Exsurge Domine non praevaleat. It is found in three medieval sources. They are (1) Le Codex 903 de la Bibliothèque Nationale de Paris (XI^e siècle): Graduel de Saint Yrieix (Paléographie musicale, XIII; Tournai, 1925), 93. (2) Le Codex VI. 34 de Le Bibliothèque Capitulaire de Bénévent (XI^e-XII^e siècle): Graduel de Bénévent avec prosaire et tropaire (Paléographie musicale, XV: Tournai, 1937), fol. 82. (3) Walter Howard Frere, ed., Graduale Sarisburiense; a Reproduction in Facsimile of a Manuscript of the Thirteenth Century . . . (London, 1894; and a reprint, 1966), 54. This bibliographical information was gleaned from John Bryden and David Hughes, An Index of Gregorian Chant; Volume I: Alphabetical Index (Cambridge, 1969), 181.

 

Although classified in all sources as Phrygian, it is only with the concluding pitch that a cadence is made to E, the modal finalis. Indeed, the pitch E is used structurally only on two other occasions: as the initial pitch, and as the registral climax approximately halfway through the melisma on the last syllable of "facie." A melodic reduction of this excerpt shows a great preponderance of motion centering on c and moving up to e and down to G. The primary structural cadences (at the "barlines") are on G, G, D, and E; the other cadences are on b, c, a, G, F, and a. The middle melisma demonstrates the characteristic Phrygian emphasis on the authentic reciting tone, c. The double neighbor approach to the finalis is present as the penultimate structural cadence falls on D and the remainder of the versus prolongs F. Note the arpeggiation F-a-c-F; a is a reciting tone in the plagal member of the Phrygian maneria.

This chant was classified as Phrygian by the compilers of the medieval tonaries on the basis of its interval species and its use of structural pitches. Phrygian did not signify "in E" to them; it would be inaccurate for us to intimate that much of this chant sounds tonally "in C." We should say that it sounds typically Phrygian! Its limited use of the pitch E corresponds exactly with the medieval theorists' view of the authentic Phrygian mode. Finalis did not signify "tonic," it meant "final pitch."

Let us briefly examine modal usages in Example 2, Trop lonc temps, a late Dufay chanson.

 

Ex. 2. Dufay, Trop lonc temps.

 

Each of the individual voice parts in the first fourteen measures of the transcription prolongs c, the Phrygian reciting tone. The superius, between measures 15-24, prolongs typical Phrygian interval species, and cadences on an e while the tenor falls to C. The melodic and tonal movement in the next phrase, measures 25-31, is quintessentially Phrygian, culminating in a perfectly-written Phrygian cadence in measure 31. The remainder of the piece moves to G, a differentia termination in both authentic and plagal varieties of the maneria while employing Phrygian interval species.

Although the chanson ends on G, it is definitely not heard in the context of a G tonality, since it employs no G-d-g Mixolydian interval species whatsoever.⁸ Fourteen of the eighty-four chansons attributed by Besseler to Dufay can be classified in this group.⁹ Seventeen other chansons are clearly in C and exhibit Phrygian characteristics similar to those present in Trop lonc temps.¹⁰

Another type of modal procedure obtains in the Dorian maneria. In this modal pair, cadential activity tends to be centered primarily around the finalis D and the cofinalis a, but also involves the difference-tone terminations on the third and fourth degrees, as well as the subtonium modi. The theorists also give the second degree structural significance as a cadential pitch, but we must search beyond plainchant practice for an explication of that locus. In the sacred music of Josquin, each of the structural pitches of the Dorian maneria is allowed to carry the species of fifth by which the mode is defined in the chant, thus creating new sets of hierarchical relationships.¹¹ Since a is the cofinalis of the Dorian maneria, it can be used to establish its own context of tonal relationships around it as a "secondary finalis." That is to say, e would be the fifth degree of a Dorian context at the level of a which is the fifth degree of D-level Dorian. What I have just described is neither a transposed mode, nor a modal mixture—as described by Renaissance theorists—but rather, a description of one of the "affinities" present in the modal system, this one between the species of fifths on D and a. In hexachordal terms, both fifths are solmisized re-la.¹²

The modal system is quite a bit more of a universe of hierarchies and procedures than many of us were taught in elementary theory courses. I believe that all tonal relationships in a piece of Renaissance music can be explained through modal procedures. To be effective, however, this explication necessarily demands as much sophistication in the understanding of modal syntax as does the high-level analysis of "tonal" music depend on a deep awareness of tonal syntax.

What seems to be indicated now is a rigorous and comprehensive study of tonal functions in plainchant, not merely a statistical tabulation of cadence loci but an explication of function and hierarchies of function. The results of this study will enable us to answer several trenchant questions. For example, do prolongations of and cadences on the subtonium modi in the Dorian maneria always serve a lower neighbor function to the finalis in the context of the complete chant? Indeed, is there a straightforward structural dominant-tonic relationship analogous to that which obtains in later music, or are there several pitches (and different ones in each maneria, I suspect) which hierarchically share that function?

Before proceeding to my second area of concern, let me reiterate the rationale behind my recommendation for a thorough study of tonal functions in plainchant with another analogy drawn from "tonal" music. When we, as sophisticated listeners, hear a piece of tonal music, we are usually not puzzled by the direction of the tonal motion. That is to say we understand even the most remote temporary tonicization in a sonata development section as one of the various possibilities available to the composer. It does not seem strange to us but merely clever. Later, once we are able to study the score, we can usually explicate the tonal movement in both linear and functional terms, confirming our initial aural judgment that the direction of the tonal movement was not capricious and arbitrary but was rather a clever and sophisticated choice among the various options built into the syntax of triadic tonality.

Consider now the last time you heard a motet by Ockeghem or Obrecht or Josquin and the number of times your ears were genuinely surprised by the direction of the tonal movement. And if you attempted an explication of that movement—as have an increasing number of music theorists (I refer especially to those who contribute to the Music Forum)¹³—you are probably too paranoid to think for a minute that such movement seems like an awkward primitive groping towards the normative triadic tonal functions of the "mature" works of the eighteenth and nineteenth centuries!

I am certain that a fifteenth-century listener did not find such progressions awkward, arbitrary and incipient! Most likely they sounded just as clever and sophisticated to him as, say, the Chopin préludes do to us, since the Renaissance listener instinctively understood modal procedures and syntax from his background in plainchant, and we do not.

The second concept of structure in music of the Renaissance I wish to discuss is the contemporary theoretical view of the repertory as dyadic, rather than triadic, in nature. Historians have been telling us this for years; the most compelling argument is given in Richard Crocker's seminal article.¹⁴ Let us now examine briefly the discant idea.

Discant is the system for teaching composition employed by music theorists from the twelfth through the sixteenth centuries, in which the student was taught how to write one-note-against-one-note counterpoint. Discant theory was concerned with the kinds of vertical sonority allowed under particular conditions, and with the principles of voice leading by which one could connect these vertical sonorities. The concern for vertical sonority resulted in a doctrine of consonance and dissonance which taught that discant is to be formed primarily of consonant intervals, and only incidentally of dissonant ones.

By the fourteenth century, the term "discant" had changed in the treatises to "counterpoint," but the basic doctrine remained unchanged. The rules for note-against-note writing developed during the fourteenth century are best summed up in Prosdocimus' Tractatus de contrapunctu, 1412.¹⁵ (1) Contrary motion is preferred; (2) the first and last intervals should be perfect consonances, but the penultimate must be imperfect; (3) two perfect consonances of the same species are forbidden in succession; (4) it is best to alternate perfect and imperfect consonances, but different perfect consonances may follow each other, and a series of two, three or more imperfect consonances of the same species is permitted if a perfect consonance follows immediately; (5) mi contra fa (the tritone) is not admissible. In addition Marchettus of Padua, in his Lucidarium Musicae Planae, V, vi-vii¹⁶ set forth the important principle which required an imperfect consonance, which he called a dissonance, to move to the nearest most perfect consonance, as a major sixth to an octave.

Prosdocimus' prohibition of parallel perfect consonances while permitting parallel imperfect consonances is quite perspicacious. Most music theorists believe that parallel motion does not produce the basic structures of any part music and that parallelism is an interruption of an anticipated resolution. From Prosdocimus' principle permitting a certain number of imperfect consonances in similar motion on the condition that the interval progression would be followed immediately by a perfect consonance, we may see how the resolution of an imperfect consonance to a perfect consonance may be interrupted by a chain of parallel imperfect consonances.

It appears certain from the teachings of the discant treatises that the contemporary music was conceived within a two-part framework. Three-part composition was always dismissed summarily with a statement to the effect that the third part was added ''as in discant"; that is to say it proceeds through the proper consonances in contrary motion with one of the other two voices. Thus from discant theory we may extract the concept of the music as a progression of intervals through time. Furthermore, the kinds of intervals available, as well as their means of progression, were specifically prescribed through the principles of consonance and dissonance and those of voice-leading.

Let us examine Example 3, a reductive sketch of the tonal movement present in Trop lonc temps, the late Dufay chanson of Example 2. The physical layout of the voice parts in the sketch reflects the dyadic nature of the music. The two discant voices, the superius and the tenor, are notated together on a single staff; the third, added voice, the contratenor, is sketched separately. The discant pair invariably closes on an octave at structural cadences, while the contratenor voice usually supplies the fifth of an 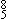sonority. The contratenor voice assumes a more structural role when it supplies a pitch with a different function, as it does in measure 20.

 

Ex. 3. Trop lonc temps, reduction.

 

The reductions were done in a manner analogous to that employed in the case of "tonal" music: short unaccented notes, neighbor notes, and dissonances were heard as non-structural. Arpeggiation notes were more problematic, since triads are not structural in this music. Generally, arpeggiations involving the structural voices, especially the superius, were included in the surface levels, as they generally fell on strong beats and thus were heard as melodically structural. Arpeggiations in the contratenor voice were frequently omitted. For example, in measure 8 the b and G do not appear in the sketch since the cadence had already been made in the preceding measure; there the contratenor behaves in a standard manner, supplying a D, the fifth of the G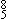. The contratenor E in measure 14 was omitted for the same reason.

The first fifteen measures present a standard prolongation of a C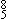 sonority, closing with a typical clausula vera (M6-P8 structural cadence). The tonal movements present in measures 4 and 7 do not constitute structural cadences as the superius—tenor dyadic framework makes imperfect consonances—a third in measure 4 and a tenth in measure 7. Only perfect consonances can be used to form structural cadences.¹⁷ Note the typical 5-5 leap in the contratenor voice at the internal cadence in measure 7.

The second phrase begins with a structural anacrusis; the parallel sixths descend finally to the octave G-g in measure 17. This sonority is prolonged as far as the Phrygian cadence in measure 31 since there is no clausula vera made until that point. Note that the textual close in measure 24 is set with a tenth between the structural voices—actually in the midst of a long chain of 10-10 dyads extending from measures 22-26, thus ignoring the textual midpoint.

The structural role of the contratenor voice in measure 20 has been mentioned previously. It is interesting to note that this cadence occurs just before the true structural voices begin their chain of parallel tenths.

The sketch substitutes a G in the tenor voice for the transcription's F in measure 33, since the descent to the C sonority in measure 35 is made through a chain of parallel sixths, as in measures 15-17. An accented passing note dissonance lasting an entire semibreve, even in tempus perfectum diminutum, completely breaks Tinctoris' rules for dissonance treatment and thus, since I am unaware of any other similar dissonance in the entire Dufay oeuvre, I judge it to be an error.¹⁸

The final level of reduction, shown by the open notes, is most interesting. The two structural voices each have the same "line." This phenomenon is quite typical of the style. I have located almost no stepwise structural movement in any Burgundian chanson. The "background" organization of the piece appears to be a series of 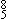prolongations. There is much contrapuntal movement within each 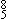prolongation, but very little between successive prolongational areas. The general avoidance of parallel perfect consonances in the foreground (primary discant procedure) and the apparent embracing of them as a unifying feature in the "background" might suggest to some that this music has different rules for different hierarchic levels! It might also suggest, if one views the work as a series of 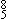prolongations, that there is no "background" at all. Another view, more in keeping with an explicative theory based on modal syntax, is that the "background" is simply the ordered set of modal structural pitches employed as cadential loci.

When Rameau published his theory of harmony early in the eighteenth century, he was obviously dealing with a different repertory. The truly revolutionary aspect of Rameau's theory lay in his realization that the vertical organization of musical space in the music of his time was triadically conceived, and that musical order is based, to a large extent, on harmonic structure. This triadic conception of vertical organization, made thoroughly practicable by Rameau's notion of triadic inversion, superseded the traditional intervallic approach to harmony. Nearly two hundred years later, Schenker clarified the confusion necessarily present in Rameau's system—because it was an incomplete system—by demonstrating the triads also have a horizontal nature. Schenker's concept of prolongation, employed to explain the horizontalization of triads, facilitated the explication of long-range hierarchies of harmonic structure in that music.

Let us now employ a bit of intuitive logic, and see where it leads us. If we accept the popular view that eighteenth- and nineteenth-century music is triadically conceived, and that tonal order can be explicated through a hierarchy of triadic prolongations, then it might be possible to view tonal order in the dyadically-conceived medieval and Renaissance repertory in terms of a hierarchy of prolongations of dyads. Just as the hierarchies of tonal prolongations in triadically-tonal music arise from factors implicit in the major and minor modes and their respective characteristic unit, the tonic triad, so are the tonal prolongations present in the dyadically-tonal music of the Middle Ages and the Renaissance dependent upon the procedures and syntactic relationships implicit in the various modes and their respective tonal units, which are the 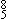sonorities composed of the characteristic species of fifth and fourth. If the skeleton of Schenker's Ursatz for triadically-conceived music is the two outer voices, say, the soprano descending 3-2-1 and the bass moving by fifths, it might not be so inconceivable that the Ursatz of a dyadically-conceived Renaissance piece could be the ordered set of cadence loci.

By proposing a dyadic interpretation of prolongational phenomena in this repertory, I am not saying that Dufay did not write V-I progressions. In fact, he wrote quite a few of them! But his awareness of the dominant function was mainly limited to one of foreground emphasis, analogous to the function of the secondary or applied dominant in tonal music, rather than to long-range directed motion. Note, for example, the third beat of measure 43 in Trop lonc temps.

I reiterate that, although the cofinalis in most modes is scale degree five, and the finalis is scale degree one, the relationship between these two structural pitches is not nearly as standardized as it becomes in later music. I hope to have demonstrated persuasively earlier in this paper that often structural pitches other than the finalis are employed as tonics. Finally, and perhaps this point, too, is obvious, a descending fifth motion in the lowest voice is but one member of a small finite set of contrapuntal possibilities for a third voice, added to the standard discant M6-P8 cadence. (See Example 2, measures 13-14,16-17, 34-35, 44, 45.) Gradually the third added voice came to function more and more as a bass line by descending a fifth at cadences. As you can readily notice, the contratenor voice is already considerably more disjunct than the members of the discant pair. The changing role of the contratenor voice is perhaps the most trenchant issue in the evolution from a dyadic to a triadic conception of musical space.

One indirect conclusion which may be drawn from the philosophy expressed in this paper is that we are not quite yet ready to trace "The Evolution of Tonality." Schenker helped show us where we ended, but since we lack a systematic explication of modal procedures and syntax, we don't really know exactly what "tonality" evolved from! Does it not make more sense to study an evolutionary pattern from both ends, rather than just by looking backwards, searching diligently for incipient dominant prolongations in twelfth-century polyphony?

We have all the tools we need. The musicological monks at Solemnes left us a complete and organized plainchant repertory while in recent years Bryden and Hughes have given us an alphabetical index with sufficient concordances and cross-references to enable us to make distinctions between older and new chants.¹⁹ Other historians have produced complete editions of most of the polyphonic repertory and are working on reliable translations of the major theoretical treatises. And we have given ourselves—with a little help from Schenker—sufficiently powerful analytical tools appropriate to a study of functional relations in any tonal repertory. What are we waiting for?

---

¹I am not, of course, insisting that composers, in their mature works, directly imitate the music to which they were exposed in their formative years; this conclusion is as inapplicable to our own contemporary composers as it is to those of the Renaissance. Our early experiences with music condition the way in which we hear more directly than they condition the music we compose. Since I believe that analysis is basically a rational, intellectual explication of an analyst's aural perceptions (both rational and irrational), rather than a futile "second guessing" of a composer's intentions, the analogy to the twentieth century was deemed valid.

²Alia Musica, ed. Jacques Chailley (Paris, 1965).

³Johannes Tinctoris, Concerning the Nature and Propriety of Tones, trans. Albert Seay (Colorado Springs, 1967), pp. 20-21.

⁴Pietro Aaron, Trattato della natura et cognitione di tutti gli tuoni di canto figurato (Venice, 1525), Chaps. 21-24.

⁵Franchinus Gafurius, Practica musicae (Venice, 1512), Bk. I, Chaps. 8-15.

⁶Pietro Aaron, Toscanello in musica (Venice, 1539), Bk. II, Chap. 18.

⁷I employ Guidonian pitch notation in which the lower octave is represented by the upper-case letters A through G, and the upper octave by the lower case letters a through g. "a" is the symbol corresponding to 220 Hz. The Guidonian gamut corresponded to male vocal ranges.

⁸Leo Treitler, "Tone System in the Secular Works of Guillaume Dufay," JAMS 18 (1965), 131-169.

⁹Frederick J. Bashour, A Model for the Analysis of Structural Levels and Tonal Movement in Compositions of the Fifteenth Century, unpublished Ph.D. dissertation, Yale University (New Haven, 1975), pp. 97-109.

¹⁰Ibid., pp. 61-81.

¹¹Leeman Perkins, "Mode and Structure in the Masses of Josquin," JAMS 26 (1973), 233.

¹²Patricia Carpenter, "Tonal Coherence in a Motet of Dufay," JMT 17/1 (1973), 12-14.

¹³For a brief critique of the articles by Salzer, Bergquist, Schachter and Novack in The Music Forum, Vols. I and II, see Bashour, op. cit., 30-39.

¹⁴Richard Crocker, "Discant, Counterpoint, and Harmony," JAMS 15 (1962), 1-21.

¹⁵Coussemaker, Scriptorum de Musica Medii Aevi, III, 193.

¹⁶Gerbert, Scriptores ecclesiastici de musica, III, 81.

¹⁷Johannes Tinctoris, The Art of Counterpoint, trans. Albert Seay (Rome, 1961), p. 20.

¹⁸Ibid., pp.113-119.

¹⁹John Bryden and David Hughes, An Index of Gregorian Chant; Volume I: Alphabetical Index (Cambridge, 1969).