During the past decade several of Schoenberg's musical compositions have begun to take their places in the standard concert repertoire. Fine recorded performances have been made available of each of his mature works; and successful live performances of major works, such as Moses und Aron and the Variations for Orchestra, have helped bring this repertoire to the musical public. In this regard, it was gratifying to find that the New York Philharmonic performed the Variations for Orchestra together with five other earlier works by Schoenberg on their 1982-83 concert series.1
The more that I hear Schoenberg's later music, the more I am struck by the fact that it sounds very much like an extension of nineteenth-century musical practice. Melodic construction, phrasing, dynamics, instrumentation, and rhythmic patterns in his music are all similar to or at least derived from nineteenth-century German and Austrian instrumental music. Why is it, then, that although listening audiences are beginning to hear and accept this music as part of the western European tradition, music theorists seem to insist that it uses a new language with different grammar and syntax than that of eighteenth- and nineteenth-century music? Such a view has been advanced by Martha MacLean Hyde with attempts to document it from Schoenberg's compositional sketches.2
The purpose of this essay is to show that Schoenberg's twelve-tone music is, in fact, an extension of the tonal musical language of his time and that perception of it as a second language is the result of a theoretical pedagogy which ignores basic harmonic concepts and normative musical practice of the late nineteenth and early twentieth centuries.
| * | * | * | * | * | * |
In his writings, Schoenberg gives us three distinct reasons for rejecting a theory of "atonality:" 1) his constant reference to music of the past as models for his own music; 2) his conservative harmonic concepts drawn directly from nineteenth-century Austrian pedagogy; and 3) his explicit disavowal of the term "atonality."
Even the most cursory examination of Schoenberg's writings reveals his preoccupation with music of the past. Among the essays collected in the 1975 edition of Style and Idea, even in the writings which are concerned with twentieth-century topics, are found numerous musical examples from and literary references to music of the late eighteenth and nineteenth centuries.3 Schoenberg uses these to establish a connection between the musical past and his own compositional style. A striking example is found in his essay, "Composition with Twelve Tones," in which he refers to serial procedures in Beethoven's String Quartet in F Major, Op. 135.4
Schoenberg's theory of the "Emancipation of Dissonance" maintains that now in twentieth-century music, in some measure, all pitches of the chromatic spectrum may be understood as having a consonant relationship with each other.5 The theory is actually an outgrowth of the harmonic premises set forth in his Harmonielehre, in which he demonstrates how all possible tertian chordal configurations can be in some way related to each other.6 This point is illustrated by the following statement given in his later book, Structural Functions of Harmony, written during his years of teaching at U.C.L.A. when he was composing mostly twelve-tone music:
Richness and greater variety of harmony are based on the relationship between a tonality and its regions, on the substitutions which are produced in the harmonies through the influence of this relationship, and on the possibility of using harmonies in a manner different from their original derivations. Many such chords deserve the name vagrant harmonies because they seem to wander nomadically between regions, if not tonalities, without ever settling down. Nevertheless, every "transformation" (altered chord) must be registered as a degree belonging to one of the regions; thus even seemingly unusual progressions will prove to be normal.7
How then is the composer to organize such a vast assortment of harmonies? Can any sort of sequence of events be allowed? The purpose of Schoenberg's Grundgestalt principle is to provide context for the organization of musical compositions, thereby providing a basis for determining the harmonic sequence of events drawn from musical practice of the past. The following statement, given by Schoenberg in his essay "Brahms the Progressive," is perhaps his most concise explanation of the Grundgestalt principle:
The most important capacity of a composer is to cast a glance into the most remote future of his themes and motives. He has to be able to know beforehand the consequences which derive from the problems existing in his material, and to organize everything accordingly.8
This statement indicates that all musical ideas must by their very nature have certain intrinsic musical meanings drawn from past associations. Hence, when the composer realizes the "utmost consequences," he is drawing upon these past meanings, albeit in a new way. Viewed from this perspective, musical language must be understood as something which constantly accumulates new meanings and new possibilities as a result of creative implementation of the old established meanings.
Professor Hyde suggests that the twelve-tone repertoire should be regarded as a second musical language for which the student must learn new rules of grammar and syntax. She maintains that to regard this repertoire as an extension of tonality is to distort its meaning. According to her, an analogy might be made with the type of distortion which occurs in translating a foreign language text directly into English. Hyde proceeds to discuss three common problems
which students have in learning to listen to atonal music: 1) the tendency to hear tonal centers, and in particular to give importance to the perfect fifth; . . . 2) the reluctance to accept complex harmonies made up of more than four pitches; . . . and 3) the resistance to hear forms not derived from tonal music.9
While I must agree that these can be problems which act as barriers to understanding twelve-tone music, I must take issue with the concept of tonality which Professor Hyde presents as her primary musical language; and hence I must reject her assumption that twelve-tone music needs to be regarded as a second language. Instead, I suggest that twelve-tone music is an extension of a single musical language, a language which has grown to incorporate many new possibilities together with older meanings drawn from the musical past.
It seems appropriate to compare music and language; Hyde's analogy, however, ignores the changing nature of language. A study of the changing language of tonality might well be compared with a study of the changing nature of the English language. Morton Bloomfield and Leonard Newmark, in their historical study of the English language, suggest:
One studies the history of the language to be liberated from a narrow view of his present language. One learns that language changes and that the "rules" of grammar are not fixed like the "Laws" of nature or the rules of artificial languages. One learns that what is now often considered a heinous solecism was not considered such a long time ago. Although one must follow certain grammatical norms in order to be considered educated, one should realize that much that has gone into the making of English is due to the replacing of some norms by others. The "errors" of the past have made present-day English for us. A language which is alive will change its rules and what is considered correct at one time may only be a current fad. This, of course, is not to say that "anything goes," but it should suggest tolerance and understanding in linguistic matters.10
The critical point here is the understanding that any language constantly changes its rules. This fact must be applied in our understanding of tonality as well. Professor Hyde's discussion of problems in understanding what she calls "atonality" betrays a narrow definition of tonality, one which denies at least some aspects of potential growth and change in the language of tonality.
Such narrowness seems to be a common aspect of many of the current music theory textbooks. Allen Forte, for example, suggests that the Neapolitan Sixth chord should be considered subdominant function. He states, "The Neapolitan chord is not the first inversion of a hypothetical triad on the lowered 2nd degree of the scale."11 Despite Forte's imposed restriction, however, the Neapolitan is, in fact, used frequently as a chord built on the lowered 2nd scale degree. Example 1 shows Schubert's use of the minor Neapolitan chord. Clearly this harmony cannot be considered part of the subdominant function since the subdominant pitch has been replaced by the lowered fourth scale degree.
Ex. 1. Schubert's use of the minor Neapolitan chord in his String Quartet in D Minor, D. 810 ("Der Tod und das Mchen"), first movement, mm. 326-332

In music literature, numerous examples are found of modulations to the Neapolitan key and even to the minor Neapolitan key. For examples of modulations to the minor Neapolitan key, see Beethoven's Third Symphony, first movement, m. 284 (an E Minor arrival in the Development section; i.e., the enharmonically spelled minor Neapolitan of E-flat Major); or Brahms's Piano Quintet in F Minor, Op. 34, first movement, m. 199 (an F-sharp Minor arrival for the beginning of the second key area material of the Recapitulation; i.e., the enharmonically spelled minor Neapolitan of F Minor). Certainly it is not reasonable to consider either of these two examples as subdominant function.
Although earlier uses of the Neapolitan sixth chord appear to be derived from subdominant function, it is obvious that composers recognized the potential of this harmony in its own right, and used it in much the same manner as they used other harmonies in the vocabulary; i.e., modulating to it and using it with interchange of mode. Whereas Forte's concept of the Neapolitan chord is a static one which allows for no changes in the meaning of the harmony, the illustrations of it from Schubert, Beethoven and Brahms cited above show the "possibility of using harmonies in a manner different from their original derivations," as Schoenberg has said in his realization of the constantly changing nature of the language of tonality.12
A similar narrow interpretation of harmony is seen in the presentation of the augmented sixth chord given in the recent theory textbook by Edward Aldwell and Carl Schachter. The authors contend that the augmented sixth chord derives from contrapuntal, not harmonic origins, involving the resolution of 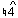 to
to 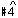 to
to 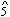 . Hence they conclude, "If
. Hence they conclude, "If 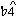 is omitted, through the technique of contraction, the interval of the augmented 6th will occupy the full duration of the chord. This certainly gives greater emphasis to the augmented 6th but does not change its essentially passing function."13 This imposed theoretical restriction denies possibilities which were, in fact, used by composers of the eighteenth and nineteenth centuries. Example 2 shows Schubert's use of the augmented sixth chord resolving deceptively.
is omitted, through the technique of contraction, the interval of the augmented 6th will occupy the full duration of the chord. This certainly gives greater emphasis to the augmented 6th but does not change its essentially passing function."13 This imposed theoretical restriction denies possibilities which were, in fact, used by composers of the eighteenth and nineteenth centuries. Example 2 shows Schubert's use of the augmented sixth chord resolving deceptively.
Ex. 2. Deceptive resolution of the German augmented sixth chord in Schubert, "Des Mädchens Klage," Op. 58, no. 3, D. 191a, mm. 11-12

*Root representatives which do not actually sound are given in parentheses.
If this harmony is regarded as a type of dominant (or secondary dominant), then it acts as a substitute for a dominant type of chord built above the root which is a major third below the upper pitch of the augmented sixth interval. Thus, for example, the so-called Italian sixth chord a-flat—c—f-sharp, the so-called French sixth chord a-flat—c—d—f-sharp, and the so-called German sixth chord a-flat—c—e-flat—f-sharp, may all be considered as substitutes for a dominant type harmony using D as its root. The common resolution of the above augmented sixth chords to G harmony represent normative dominant-tonic resolutions. If the harmony resolves to an E-flat Major chord, as in the example, this may be considered a deceptive resolution. In this case, of course, the augmented sixth interval still resolves outward to the expected octave as described by Aldwell and Schachter.
But what about the resolution shown in Example 3?
Ex. 3. Mozart's deceptive resolution of an augmented sixth chord, Piano Concerto in C Minor, K. 491, first movement, mm. 1-14, in which the outer extremes of the augmented sixth interval resolve inward

In this case, Mozart resolves the substitute for D harmony not to its expected tonic G, nor to its submediant E-flat as in Example 2, but to B-flat, i.e., the dominant of its submediant. Certainly the resolution of V to V/VI is now understood to be a regular aspect of the language of tonality. One may, of course, regard this example as a delayed resolution to the tonic 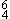 chord in bar 12 of the excerpt. In the larger context of a movement in which an interplay between the keys of C Minor and E-flat Major is significant at many different levels, however, the resolution of the augmented sixth chord in the region of C Minor to the dominant chord of E-flat Major at a point so early in the first phase of the movement takes on a special significance. The theoretical framework presented by Aldwell and Schachter does not allow for this possibility since
chord in bar 12 of the excerpt. In the larger context of a movement in which an interplay between the keys of C Minor and E-flat Major is significant at many different levels, however, the resolution of the augmented sixth chord in the region of C Minor to the dominant chord of E-flat Major at a point so early in the first phase of the movement takes on a special significance. The theoretical framework presented by Aldwell and Schachter does not allow for this possibility since 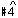 passes to
passes to 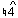 and not to
and not to 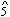 . Mozart's treatment of the augmented sixth chord illustrates his creative interpretation which provides a new meaning for augmented sixth harmony. Again, as with Forte in his discussion of the Neapolitan chord, the explanation of the augmented sixth chord given by Aldwell and Schachter is presented in a framework which is too narrow to explain the breadth of musical practice. These are but two examples of harmonies which are given restrictive definitions in current music theory textbooks. Such theoretical restrictions provide the student with false notions regarding the limits or potentialities of tonality.
. Mozart's treatment of the augmented sixth chord illustrates his creative interpretation which provides a new meaning for augmented sixth harmony. Again, as with Forte in his discussion of the Neapolitan chord, the explanation of the augmented sixth chord given by Aldwell and Schachter is presented in a framework which is too narrow to explain the breadth of musical practice. These are but two examples of harmonies which are given restrictive definitions in current music theory textbooks. Such theoretical restrictions provide the student with false notions regarding the limits or potentialities of tonality.
Schoenberg's own explanations of these chromatic harmonies are considerably different from the restrictive explanations cited above. He explains the Neapolitan as subdominant of the submediant (IV/VI).14 Hence it is treated as a diatonic chord in a secondary region. Schoenberg's explanation of the augmented sixth chord as a dominant substitute is the same as that cited above.15 This explanation is apparently derived from the nineteenth-century Austrian theorist Simon Sechter.16 Sechter describes the augmented sixth chord as a Zwitterakkord (literally "bastard" or "hybrid" chord) because it has the two contradictory elements: a major third derived from major harmony and a diminished fifth derived from diminished harmony. According to Sechter, the chord can be built above any diatonic root and the interval of the augmented sixth, or its inversion the diminished third, normally resolves in contrary motion by semitone to a harmony which has its root a perfect fifth lower than the actual root of the Zwitterakkord.17 Thus the Zwitterakkord may be used to intensify the harmonic drive in a progression of perfect fifths. In the diatonic circle of fifths, the augmented sixth, or its inversion, may occur between any pair of chords except between IV and VII in the major mode or between VI and II in the minor mode, since the roots in each of the two latter successions are a diminished fifth apart. Sechter's illustrations of the use of the Zwitterakkord in the diatonic circle of fifths are shown in Example 4.
Ex. 4. Sechter's illustrations of the Zwitterakkord in the diatonic circle of fifths of A Minor

This pedagogical framework, first presented by Sechter and later used by Schoenberg, allows for possible deceptive resolutions as shown in Examples 2 and 3, some of which may not necessarily incorporate the linear expansion of the augmented sixth to the octave—or 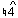 to
to 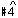 to
to 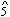 as presented by Aldwell and Schachter.18
as presented by Aldwell and Schachter.18
Schoenberg's harmonic concepts are neatly summarized in his Harmonielehre. He recognizes that all harmonic successions may be reduced to three types: 1) strong or ascending (up by fourth or down by third) 2) weak or descending (down by fourth or up by third); and 3) super-strong (up or down by step).19 He goes on to explain that all chromatic changes in harmony occur above diatonic chord roots.20
Although Schoenberg refers in the text of Harmonielehre to several theorists, the only one of these from whom it can be said Schoenberg has appropriated actual harmonic concepts as part of his own thesis is Simon Sechter.21 Schoenberg's thesis that all harmonies may be thought of as related to each other in the same manner that diatonic degrees of the scale are related to each other is not only an early twentieth-century realization of nineteenth-century Austrian harmonic pedagogy incorporating common chromatic idioms of the early twentieth century into this ultraconservative framework, but it also establishes a basis for perceiving the foreground of music as the source of its logic—a concept diametrically opposed to Schenker's Ursatz theories.22
Reliance upon Schenker for a definitive statement regarding the nature of tonality has led Forte, Aldwell and Schachter, and Hyde to the conclusion that the primary musical language will no longer serve to explain twelve-tone musical practice.23 None of these writers incorporates the chromatic language of late nineteenth- or early twentieth-century music into his or her presentation of harmonic principles. But it must be remembered that Schenker did not represent the mainstream of musical thought in his day. He categorically rejected the compositions of Richard Strauss, Mahler, and Reger, and was exceedingly uncomfortable with the harmonic practice of Bruckner and Wagner.24 How can a concept, formulated in the early part of the twentieth century, which denies the inclusion of then current harmonic practice, be regarded as a norm for defining the primary language of tonality? Interesting and informative as Schenker's ideas about musical construction may be, if one is to gain an honest perspective of late nineteenth-century music, his must be regarded as an overreaction to the excesses of ultraconservative pedagogy of Sechterian teaching.25 Adoption of Schenker's definition of tonality leaves us no choice but to regard nineteenth-century normative chromatic practice as the breakdown of the primary musical language of tonality.
Schoenberg's applications of the ultraconservative view, on the other hand, provide a basis for perceiving his own music as an extension of this primary language. The whole-tone scale, which Forte and Hyde regard as an incipient aspect of what they regard as "tonality,"26 is presented in Harmonielehre as an extension of tertian harmony arising from the use of augmented triads and altered dominant seventh chords with raised fifths.27 Schoenberg also discusses quartal harmony as an extension of traditional harmonic practice.28
The language of tonality as it existed in 1920, at the time when Schoenberg formulated his twelve-tone method of composition, included all of the above-mentioned harmonic possibilities as regular or normative aspects. If today's music student is to approach the twelve-tone repertoire in an intelligent manner, he must have a theoretical grasp of this language and must not be restricted by theoretical explanations of specific harmonies which ignore common harmonic procedures from Schoenberg's time.
Example 5 shows the harmonic progression found in mm. 41-53 from the third movement Scherzo of Bruckner's Seventh Symphony in E Major, a characteristic example of late nineteenth-century chromatic practice.
Ex. 5. Bruckner, Seventh Symphony, third movement, mm. 41-53, harmonies and their fundamentals

Below each harmony is given the fundamental, according to the harmonic principles set forth by Sechter and restated by Schoenberg; below the fundamentals Sechterian derivations of the chords are explained. The example illustrates a consistent harmonic gesture of alternating downward third and downward fifth progressions. The downward third progression is a consistent part of the musical language of this work announced through its very first harmonic succession in the first movement: an E Major chord followed by a C Major chord. This first gesture forecasts many long range aspects of the entire symphony and is realized in numerous passages throughout the work. Despite the linear nature of the bass line in Example 5, Schenker's theory is of limited value for explaining it since much of the logic of this passage has more to do with submediant relationships, suggested by the work's first harmonic gesture, than with outlining the tonic triad.29
| * | * | * | * | * | * |
"Atonality" is a term first coined by music critics to indicate the lack of musical skill and understanding that they thought they perceived in music of the early twentieth century. Similar criticisms have been made of virtually all of the great composers of the past.30 The term "atonality" seems to be used now by music theorists to attempt to explain music which cannot be explained in terms of current pedagogies of tonality. With the exclusion of nineteenth-century Austrian harmonic pedagogy from current presentations of this topic, a gap has been created by music theorists; hence the need for a second language has arisen. It seems that Schenker's narrow conception of tonality, as one with fixed limits, has made a separate theory necessary for explaining twentieth-century music.
Let us examine Hyde's contention that students rely too much upon tonal centers, and specifically upon the perfect fifth, when listening to twelve-tone music. The first movement of Schoenberg's Woodwind Quintet, Op. 26, is developed from two six-note figures which bear a close resemblance to a fugal subject and its adjusted answer from eighteenth- and nineteenth-century contrapuntal practice. As shown in Example 6, these two figures have a potential tonic-dominant relationship with the subject or dux beginning on E-flat, and the answer or comes on B-flat, its dominant. Only the last interval has been adjusted in the comes.31
Ex. 6. Schoenberg, Woodwind Quintet, Op. 26, first movement: the dux (flute, mm. 1-4) and the comes (oboe, mm. 16-17)

The specific twelve-tone row and the method32 of its employment serve to assure that E-flat and B-flat are significant absolute tonal reference points in the entire work. The interrelation between E-flat and B-flat is easily identifiable in the first movement through timbral and rhythmic associations in mm. 1, 41-42, 127-28, and 205-6. In each instance, the B-flat is sounded first by the horn on a sustained note, followed by the thematic line in one of the other instruments in which the pitch E-flat is prominent. I submit that Schoenberg is using the absolute pitch relationship E-flat—B-flat to articulate the form of the movement. The places cited above are, respectively, the beginning of the first theme and second theme of the Exposition, the beginning of the first theme in the Recapitulation, and the beginning of the Coda, as shown in Example 7.
Ex. 7. Examples of the interrelation between E-flat and B-flat in the first movement of Schoenberg's Woodwind Quintet:
a) Beginning of the first theme of the Exposition, meas. 1

b) Beginning of the second theme of the Exposition, mm. 41-42

c) Beginning of the first theme in the Recapitulation, mm. 127-28

d) Beginning of the Coda, mm. 205-6

Two other places in the movement are worthy of comment in regard to emphasized perfect fifths and absolute pitch references. In m. 160, the bassoon plays a sustained E-flat to which the flute responds in m. 161 with the dux phrase beginning on A-flat; immediately following this, the horn sounds a sustained B-flat to which the oboe responds with the dux now starting on E-flat. Thus the tonic pitch E-flat in the bassoon serves as V/IV followed by a subdominant entry in the flute; and this dialogue is, in turn, transposed one measure later back to tonic level. As shown in Example 8, the rhythms of these paired dialogues are the same. Hence Schoenberg uses timbral and rhythmic associations to reinforce absolute traditional tonal references.
Ex. 8. Tonic-Subdominant and Dominant-Tonic relationships in Schoenberg's Woodwind Quintet, Op. 26, first movement, mm. 160-63

Another instance of this subdominant relationship, as shown in Example 9, is found in m. 171. At this point, the horn sounds a sustained E-flat to which the flute responds with an inverted dux in diminution starting on G-sharp (enharmonically A-flat).
Ex. 9. Tonic-Subdominant relationship in Schoenberg, Woodwind Quintet, Op. 26, first movement, m. 171.

Clearly in all of these instances, Schoenberg intends to emphasize certain pairs of pitches which are not only a perfect fifth apart, but, more importantly, which may be understood as dominant-tonic and tonic-subdominant within the context of the movement. Hyde contends that Schoenberg's sketches illustrate the fact that he was attempting to avoid the perfect fifth interval. However, it seems much more likely that Schoenberg was avoiding simultaneous and successive references to the absolute pitches E-flat and B-flat in order not to create the sense of false return at a premature point in the movement. While I must concur with Professor Hyde that careful study of the sketches is important, it is essential that any interpretation of them take into account the nature of the musical language of tonality as it existed at this time and the specific manner in which the musical gestures of the given composition makes use of that musical language.
As part of her argument "to discourage student suspicion that fifths are there for them to grasp," Hyde cites the following quotation from Schoenberg's essay, "Twelve-Tone Composition:"33
In twelve-tone composition consonances (major and minor triads) and also the simpler dissonances (diminished triads and seventh chords)—in fact almost everything that used to make up the ebb and flow of harmony—are, as far as possible, avoided. . . . At the root of all this is the unconscious urge to try out the new resources independently, to wrest from them the possibilities of constructing forms, to produce with them alone all the effects of a clear style, of a compact, lucid and comprehensive presentation of the musical idea. To use here the old resources in the old sense saves trouble—the trouble of cultivating the new—but also means passing up the chance of enjoying whatever can only be attained by new resources when the old ones are excluded!34
Two important points need to be raised in response to Hyde's interpretation of this quotation: 1) Nowhere does Schoenberg say that perfect fifth relationships are to be avoided. What he does say is that traditional surface phenomena, and in particular tertian sonorities, should not be the means of organizing tonal relations. It is the means of organization that Schoenberg is referring to here. This statement gives context for Schoenberg's contention that twelve-tone writing is a method and not a system. The term "method" implies a means toward an end. At least in the case of the Woodwind Quintet, the first movement is organized around absolute pitch centers E-flat and B-flat and to a lesser extent A-flat—pitches which, as seen above, have a traditional meaning. The twelve-tone method finds a way of interrelating these traditionally established pitches without using tertian sonorities. This is the meaning of Schoenberg's quotation. If, however, one regards twelve-tone music as a system, then one must see the serialization of pitches as an end in itself rather than as a means—an idea contrary to Schoenberg's intention.35
2) It must be remembered that this quotation comes from a time when Schoenberg was first developing his twelve-tone method. Tertian sonorities do, in fact, occur in many of his later twelve-tone works. An oft-cited example is the E-flat Major triad in the Ode to Napoleon.36 Others are found in the Third String Quartet, where there is an augmented triad (shown, in Example 10),
Ex. 10. Augmented triads in Schoenberg, Third String Quartet, Op. 30, first movement, mm. 48-51

and in the Variations for Orchestra, where a thematic line sounds like the upper tetrachord of the harmonic minor scale, and where one finds the complete diatonic circle of fifths in a bass line (shown in Example 11).37
Ex. 11. Surface phenomena of tertian harmony in Schoenberg, Variations for Orchestra, Op. 31
a) Upper tetrachod of F harmonic minor in Hauptstimme at beginning of Variation 7, preceded by the dominant tritone of F Minor in the Nebenstimme at end of Variation 6, mm. 236-38

b) Complete diatonic circle of fifths in the bass line of the first phrase of Variation 4, mm. 134-35
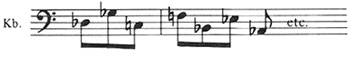
Hyde's second contention that students tend to disbelieve the existence of complex chordal sonorities of more than four pitches is also the result of teaching a restrictive concept of tonality. Schenker complains about leere Vierklänge in music by Richard Strauss, Mahler, and Reger, among others.38 Yet such complex chords were the common property of the early twentieth century and all may be explained by means of the Sechter-Schoenberg harmonic framework discussed above.
The third contention that students have difficulty with forms not derived from tonal practice is likewise a result of a too-narrow concept of tonality. Application of Schoenberg's Grundgestalt principle shows that although certain formal categories are common—e.g., sonata, rondo—, musical forms are not generic types, but rather expressions of the potentialities of musical ideas.39 As the language of tonality becomes gradually more and more complex, it is only natural that the projection of these ideas into musical forms likewise takes on more complex architectural realizations.
Just as the English language is constantly changing, so is the language of tonality. Every new creative work extends the various meanings of gestures and permits in some way new possibilities for organizing musical thought. Some of these new creative works have appeared to challenge the very basis of musical language itself. In particular, the immediate impact has been to suggest that a new musical language has been formulated. This phenomenon may be seen with the arrival of Beethoven's Eroica Symphony or Wagner's Tristan und Isolde, as well as Schoenberg's Woodwind Quintet, Third String Quartet, or Variations for Orchestra, to mention a few examples. But time has served to soften the differences which appeared so strikingly at the time these works were first performed publicly. Beethoven and Wagner are certainly perceived today as central figures in the musical tradition represented by its primary language of tonality, and their creativity is explained in the theory classroom as the realization of the logic of this language. Schoenberg's twelve-tone works are now fifty years old and are beginning to be accepted as part of our musical tradition. Pedagogies of music theory must take this tradition into account. When the nineteenth-century conservative Austrian pedagogy is incorporated into our understanding of tonality, then comprehensive musicianship will have found a "single set of analytical categories which will form the groundwork of later studies in music."40 Armed with this information, the student will have access to the contextual significance of Schoenberg's twelve-tone music.
Hence it is important for the theorist to explain twelve-tone music as a logical extension of the primary language of tonality. Professor Hyde, in making an analogy between music and language, needs to recognize the changing nature of language and the corresponding changes in music which, in this case, lead to twelve-tone music.
| * | * | * | * | * | * |
If the arguments stated above are not enough to justify a rejection of a theory of "atonality," the clinching argument should be Schoenberg's own rejection of the term. In a footnote to the third edition of Harmonielehre, he says,
. . . I am a musician and have nothing to do with things atonal. The word "atonal" could only signify something entirely inconsistent with the nature of tone. . . . Everything implied by a series of tones constitutes tonality, whether it be brought together by means of a direct reference to a single fundamental or by more complicated connections. That from this single correct definition no reasonable opposite corresponding to the word "atonality" can be formed, must be evident. . . . To call any relation of tones atonal is just as farfetched as it would be to designate a relation of colors as aspectral or acomplementary. There is no such antithesis. Besides there has been no investigation at all of the question whether the way these new sounds go together is not actually the tonality of a twelve-tone series.41
According to Schoenberg's concepts about harmony and the use of the word "atonality," one might legitimately say: There is no atonality in music, only acontextuality in music theory. Let us restore the context from Schoenberg's own writings and see what we can learn about late nineteenth- and early twentieth-century music as well as about twelve-tone music.
1Other works by Schoenberg performed during the 1982-83 season were: Pelleas und Melisande; Chamber Symphony, Op. 9; Erwartung; Five Pieces for Orchestra, Op. 16; and Gurrelieder.
2Martha MacLean Hyde, "Schoenberg's Sketches and the Teaching of Atonal Theory," College Music Symposium 20, No. 2 (Fall 1980), 130-37.
3Arnold Schoenberg, Style and Idea, ed. Leonard Stein, trans. Leo Black (New York: St. Martin's Press, 1975). In particular see "Composition with Twelve Tones (1)," pp. 214-45.
4Ibid., pp. 220-22.
5Ibid., pp. 216-17. Schoenberg refers here to dissonances as "the more remote consonances."
6See my review of Maurice J.E. Brown, "Sechter, Simon," The New Grove Dictionary of Music and Musicians in Nineteenth-Century Music 5, No. 2 (Fall 1981), 167-68, and Robert W. Wason's review of Arnold Schoenberg, Theory of Harmony, trans. Roy E. Carter, in Journal of Music Theory 25, No. 2 (Fall 1981), 311-14, for discussion of this point.
7Arnold Schoenberg, Structural Functions of Harmony, ed. Leonard Stein, (New York: W.W. Norton, 1954), p. 35.
8Schoenberg, "Brahms the Progressive," Style and Idea, p. 422.
9Hyde, "Schoenberg's Sketches," pp. 133, 134, and 137.
10Morton W. Bloomfield and Leonard Newmark, "Language and the History of Language," English Then and Now, ed. Alan M. Markman and Erwin R. Steinberg (New York: Random House, 1970), p. 23.
11Allen Forte, Tonal Harmony in Concept and Practice, 3rd ed. (New York: Holt, Rinehart and Winston, 1979), p. 360.
12Schoenberg, Structural Functions of Harmony, p. 35.
13Edward Aldwell and Carl Schachter, Harmony and Voice Leading (New York: Harcourt Brace Jovanovich, Inc., 1979), II, 164.
14Schoenberg, Structural Functions of Harmony, p. 35. This explanation is also given in Walter Piston, Harmony, 4th ed., rev. Mark DeVoto (New York: W.W. Norton, 1978), p. 406.
15Schoenberg, Theory of Harmony, trans. Roy E. Carter (Berkeley: University of California Press, 1978), pp. 245-49. A similar explanation is found in Piston, Harmony, p. 416.
16This point is discussed in my article, "A Response to Schenker's Analysis of Chopin's Etude, Op. 10, No. 12, Using Schoenberg's Grundgestalt Concept," The Musical Quarterly 59, No. 4 (Fall 1983), 548-52.
17Simon Sechter, Die Grundsätze der musikalischen Komposition (Leipzig: Breitkopf und Härtel, 1853-54), I, 146-52.
18For further unusual resolutions of the augmented sixth chord, see Schoenberg, Theory of Harmony, pp. 255-56.
19Ibid., pp. 115-23.
20Ibid., pp. 192-93, and 245-48. See also n. 7 above.
21Schoenberg refers to Sechter by name only once in Theory of Harmony, p. 270. See also translator's footnote on p. 113. The derivation of Schoenberg's ideas from Sechter's theories is covered in my "Response to Schenker's Analysis," 542-69.
22Ibid.
23In particular, see Allen Forte, "Schoenberg's Creative Evolution: The Path to Atonality," The Musical Quarterly 64, No. 2 (April 1978), 159-65, in which the author attempts to use Schenkerian methodology to explain "tonal" aspects of Schoenberg's music.
24Heinrich Schenker, Kontrapunkt I (Stuttgart, 1910), p. xvii, denounces Richard Strauss, Mahler, Reger, Humperdinck, and Pfitzner because their music cannot be explained in terms of his Ursatz theories. In Der Tonwille 1, 25, he compares Wagner to Karl Marx as a genius who has led lesser composers astray. In Der Tonwille 5, 46 and "Über Anton Bruckner," Der Dreiklang 7 (October 1939), 166-76, Schenker displays an irritable attitude toward Bruckner and criticizes him for not adhering to Ursatz concepts.
25This attitude is clearly revealed in his article "Über Anton Bruckner."
26In this connection, Allen Forte, "Schoenberg's Creative Evolution," p. 148, refers to the French augmented sixth chord as an "incipient atonal pitch-class set" and as a "formation not characteristic of triadic tonality" when it appears in root position.
27Schoenberg, Theory of Harmony, p. 391.
28Ibid., pp. 399-410.
29See n. 24 above.
30For examples in the nineteenth and early twentieth centuries, see Nicolas Slonimsky, Lexicon of Musical Invective (New York: Coleman-Ross, 1953).
31This point is discussed by Anton Webern in The Path to the New Music, ed. Willi Reich, trans. Leo Black (Bryn Mawr, Pa.: Theodore Presser, 1963), p. 54. For further discussion of traditional tonic and dominant relationships in twelve-tone music see my article "Tonality in Webern's Cantata I," forthcoming in Music Analysis.
32Schoenberg preferred the term "method" to that of "system" in reference to twelve-tone music. For a thorough discussion of this point see my "Schoenberg's Grundgestalt Principle: A New Approach with Particular Application to the Variations for Orchestra, Opus 31." (Ph.D. dissertation, University of Cincinnati, 1976), pp. 393-400.
33Hyde, "Schoenberg's Sketches," pp. 133-34.
34Schoenberg, "Twelve-Tone Composition," Style and Idea, p. 207.
35For current pedagogical approaches which refer to twelve-tone composition as a "system," see Allen Forte, The Structure of Atonal Music (New Haven: Yale University Press, 1973); John Rahn, Basic Atonal Theory (New York: Longman 1980); and Charles Wuorinen, Simple Composition (New York: Longman, 1979).
36In a letter cited in Arnold Schoenberg, Letters, ed. Ersin Stein, trans. Eithne Wilkins and Ernst Kaiser (New York: St. Martin's Press, 1965), p. 248, the composer states, "It is true that the Ode at the end sounds like E flat. I don't know why I did it. Maybe I was wrong, but at present you cannot make me feel this."
37A lengthy discussion of this point is given in my dissertation, "Schoenberg's Grundgestalt Principle," in regard to the Variations for Orchestra and the Fourth String Quartet.
38Schenker, Kontrapunkt I, xvi.
39This point is discussed in detail in Josef Rufer, Composition with Twelve Notes Related only to one Another, trans. Humphrey Searle (London: Barrie and Jenkins, 1954), pp. 166-76.
40Hyde, "Schoenberg's Sketches," p. 131.
41Schoenberg, Theory of Harmony, p. 432.


