Not long ago I visited my local automobile dealer. Attracted by the low sticker price, I explained to the salesman I had no inclination to purchase any of the long list of extras affixed to the side window. "But you will have to pay $169 for the rear window wiper," the salesman explained. "We want to keep the sticker price low, but every car comes with the rear window wiper. So, you have to buy it. It's a mandatory option."

Mandatory option is a telling example of the doublespeak that pervades the language of business and politics. It is also a striking example of an oxymoron. "Good grief," you exclaim! "What's an oxymoron?"

An oxymoron (I reply) is a figure of speech in which incongruous, contradictory terms are united to a single idea—such as good grief. Appropriately, the word oxymoron is itself oxymoronic because it is formed from two Greek roots of opposite meaning: oxy, meaning "sharp or keen," and moros, meaning "foolish or dull." Additional examples of word parts oxymoronically drawn together into one word are pianoforte ("soft/loud") and sophomore, meaning "wise-fool." If you know any sophomores, you realize how perfect that oxymoron is.

Perhaps the most famous example of an oxymoron in this country is one from comedian George Carlin's LP recording Toledo Window Box. The example is jumbo shrimp. Expand the expression to fresh-frozen jumbo shrimp and you have a double oxymoron. Once the concept is planted, these miniature paradoxes begin to sprout everywhere: guest host, original copy, recorded live, standard deviation, plastic silverware, death benefit, peace offensive, designer jeans, postal service, and military intelligence.¹

A study of internal contradictions in language has caused me to wonder whether similar situations might be found in music—that is, events, patterns, relationships, perhaps even single notes that exhibit contradictory or opposite meanings. One musical candidate can be found in Beethoven's Piano Sonata, Op. 10, No 1 (3d movement).

 

Figure 1. Beethoven, Piano Sonata in C minor, Opus 10, No. 1, 3d Movement.

 

At the start of the development the polar key of 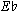continues. An appoggiatura is initiated in the 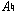bass of measure 46, and is imitated in 47 by D; in 48 with 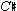first, then 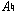again; and in 49 with 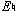. The pattern is thus well set in the ear as movement into measure 50 continues. At first listen, and maybe even second listen, the right-hand 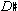on the downbeat of 50 seems to correspond in function to the 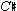on the downbeat of 48—that is, it sounds like an appoggiatura resolving up by half-step. And it is. But, at the same time (and unlike the earlier cases), when enharmonically reinterpreted as an 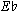, it is also a chord tone—the resolution of measure 49's dominant harmony.

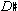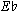The conflicting meanings can be uncovered if we imagine measure 50 as the pivot chord of a fleeting modulation to f minor. Contrary to normal pivot situations, this common chord is a stable major-quality tonic arrival in the old key and an active diminished chord in the new. What is remarkable about this case is not the enharmonic respelling ( to ) or the switch in functional meaning (tonic becomes dominant), but rather that the 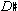can operate as an anchored consonance and as a restless dissonance at one and the same time. Is 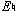or 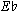the root of that chord? Is 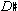an appoggiatura or is 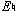a kind of alto-register chromatic passing tone to F? Or are all of these interpretations true at once? Such witty and slippery aural sleights of hand seem to incorporate the same kind of craft and appeal that are found in word play such as oxymorons, puns, and, on a lower level, knock-knock jokes.

The relatively quick tempo almost disguises the trick; the event is over before we realize what has happened and we find ourselves responding with a listener's double-take. The surprise is not that the stable 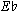slides so quickly (in harmonic banana-peel fashion) into a tritone-loaded dominant of f minor, but rather that the initial event of that measure was itself stable when none of the previous ones were. If a harmonic banana peel is defined as the replacement of a sure-footed arrival by a slick and unexpected substitute chord, then the beginning of measure 50 is the opposite: expected instability is replaced by solidity, But the trick is double-edged. The sturdy 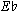chord instantly liquefies, as a destabilized 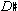turns out to be an appoggiatura after all.

Another Beethoven piano sonata (Op, 22, 2d movement) involves an equally peculiar situation.²

 

Figure 2. Beethoven, Piano Sonata in 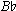major, Opus 22, 2d Movement.

 

At times, the right-hand melody seems curiously outside the unequivocal 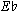tonality established underneath. Witness, for example, the incursion of 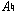into the tonic field in measure 2 and especially the unruly swatch of sound in measure 3. The contradictions, though, are more subtle and complex than simple nonharmonic tones.

By comparison with the beginning of measure 2, where the 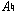appropriately resolves to 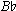, the 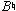of measures 2 and 3 similarly ought to resolve to C. C, in fact, has just been briefly welcomed into the diatonic collection as an ornamental upper neighbor. The plot thickens as we continue further into measure 3, The expected C does materialize, but not as a stable follow-up (like the 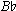resolution of measure 2). Instead, it merely decorates (as part of a turn figure) the reigning 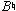. However, even the secure arrival of C would not be very satisfying anyway in light of the switch to dominant-seventh harmony underneath.

By comparing the beginning of measure 3 with the two earlier turn-like figures in measures 1 and 2, the melodic line in measure 3 has completely derailed in relation to the supporting harmony. Only one of the first seven melody notes even belongs to the prevailing dominant-7th chord—and it involves perhaps the most bizarre usage of all. I direct your attention to the soprano D on the 3d eighth. This potentially stable note clarifies nothing since the melodic line is still seeking out a C. In the normal context of a dominant-7th in 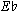, the pitch class D, of course, is a leading tone. Here, however, even though it belongs to the V⁷, it is an outsider—a highly dissonant intensifier of the long-awaited, yet barely achieved, C. We have, then, in the beginning events of measure 3, a chord-tone D in the bass sounding against another D in the soprano with an opposite meaning. An odd flicker of tension is felt, as a note paradoxically becomes dissonant against itself. Unlike the previous Beethoven example, where a single pitch contained two meanings, here two different versions of the same pitch project contradictory functions. Further pitch events in this movement (e.g., see the development section) provide a cornucopia of additional aural confusions and sleights of hand.

 

Figure 3. Bach, Sinfonia in F minor.

 

Another example involves the opening measure of Bach's F-minor Sinfonia. The upper-voice 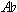appears to be a consonant 3d sounding over the tonic bass. As events unfold, however, it becomes evident that the 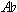, in fact, resolves—moving down to G. The intervallic movement is m10 to M9 (a 3-2 resolution pattern, if you will—and a strange reversal of our usual sense of how dissonant intervals resolve to consonant ones, not the other way around). The F in the bass then becomes reinterpreted as a dissonance itself against the G and resolves to 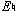. Perhaps the true intervallic relationship, then, is 2-3, not 3-2. In my view, however, the twisting contour of the three-note right-hand motive, with its short up-beat leap from F to the rhythmically stronger 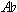, imbues that supposedly static tonic-triad pitch 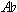with an urgency—even a discordance—that is dispelled as it sinks back into the relatively more secure G. Similarly, the 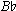soprano resolves to 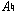, forcing us, curiously, to regard the resulting tritone (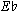-A) as a relatively more stable simultaneity than the P5 from which it emerges.

The entire piece continues with an incredibly rich interplay of various double meanings—the finely tuned harmonic and rhythmic control confusing our traditional categories of dissonance, consonance, and resolution (see, for example, mm. 7-8). Even at a slow tempo a compelling sense of forward drive is achieved. Rarely has such dense expression been compressed into three minutes of clock time. There is simply more music per unit of time here than in many more diluted pieces of the same length.

As we have just heard, expressive resonance in music can grow out of the multiple meanings that result from contradictory signals. Returning to language, let me offer some illustrations of sentence-structure incongruities found in typical letters of recommendation. In each case, some kind of internal contradiction or ambiguity of syntax or meaning is involved so that each comment could be construed in two different—even opposite—ways. They are loaded, in other words, with linguistic banana peels. Such statements could potentially be highly useful to letter writers who wish to disguise their true feelings or, on the other hand, could be the source of unintended hilarity when ineptly written or misread. As in music, the intended or purposely vague meaning can often be highlighted or obscured depending on delivery and interpretation. In this case, two different readings could be:

"I am pleased to say this candidate is a former colleague of mine." OR

"I am pleased to say this candidate is a former colleague of mine."

Here are a few more, with the interpretation left up to the reader:

"I most enthusiastically recommend this candidate with no qualifications whatsoever."

"In my opinion, you will be very fortunate to get this person to work for you."

"I would urge you to waste no time in making this candidate an offer of employment. "

"All in all, I cannot say enough good things about this candidate or recommend him too highly."

And finally,

"I can assure you that no person would be better for this job."³

Such self-contradictory constructions can serve purposeful artistic ends, as in fine literature and music; or they can be the result of inadvertent bungling.

Opportunities for using incongruities to stimulate thinking in teaching music theory are available even within the confines of rudiments classes. After spelling augmented and diminished 4ths and 5ths (let's say up from middle C), it can be revelatory to assign a class to notate an augmented unison (C to 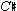) and then, with a straight face, to request a diminished unison from the same pitch. As they rush to write C-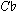, and then pause to reflect, one can almost hear the wheels spinning as they mull over the real meaning of "diminished" and confront the contradiction they have produced.

Likewise, after studying the key signature rule-of-thumb (i.e., the network of one accidental more or less for closely related keys), it is worthwhile to throw open for class discussion the question, "Are D major and d minor closely-related?" As they bump against the limitations of the rule, it will occur to some that if conventional instances of close connections involve sibling-like bonds of relatedness, then parallel scales are practically Siamese twins. The puzzle, or contradiction, of how keys that share the same tonic can be closely related, yet not follow the key-signature rule seems ridiculously simple-minded to us as theory teachers, but provides a marvelous entry point into the mysteries of functional tonality for the beginner as apparent mismatches are revealed between defined precepts or abstract paradigms, on the one hand, and real musical situations, on the other.

Additional inconsistencies include the two-fold function of pivot chords in modulation (the backward vs. the forward looking duality) and, on a more sophisticated plane, the hierarchical distinction between immediate and long-range functions of individual chords in cadence patterns.

 

Figure 4.

 

A V/V is, of course, pre-dominant in the larger tonal context but dominant at the local, chord-to-chord level. Even simple progressions that we as teachers take for granted can be made to seem fascinating and rich if presented as intriguing patterns of double meaning.

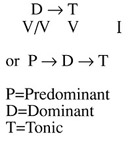
At a more advanced level, the N⁶ chord is a particularly controversial case because of its false consonance. Disappointingly, only one out of about fifteen current undergraduate theory and harmony texts I have examined seems to fully acknowledge its paradoxical nature. The chord is practically always defined as a first-inversion major triad built on the lowered second scale degree; but in reality, inversion theory rarely applies—although thinking of the chord in this way does have some value for spelling the notes accurately. Except in cases where the N is tonicized, however, the so-called root (e.g., 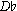in the key of C) is actually a highly dissonant note—the opposite of what we would expect from the conventional explanation. More likely, that note displaces the 5th of a minor iv chord—as a kind of frozen (i.e., nonresolving and falsely consonant) appoggiatura. The standard Phrygian explanation is not very convincing either.

 

Figure 5.

 

If anything, the 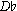is an inflection (i.e., a momentarily borrowed 6th scale degree) of the subdominant. What is at stake here is not simply fussy distinctions in definition but the very essence of pitch study: which pitches give meaning and which take meaning. The common textbook description is a kind of figure/ground reversal. The F in the bass is not the 3d generated from a fundamental but rather is itself the generating source from which the sounding above acquires its quasi nonchord status. To call the root makes about as much sense as saying that "flapping flags cause the wind's turbulence," a case of the vertical tail wagging the linear dog.

Tonal answers in fugue study also illustrate how contradiction can be exploited in teaching counterpoint. It is easy to get bogged down with complex rules about numbering scale degrees or changing this interval to that. The contradiction here is that the tonic centricity of the initial subject entry must be permitted to spill over into the transposition of the dominant-level answer, to avoid too early and too jarring a swing of tonal loyalties. A certain controlled amount of "tonicness" must infiltrate the dominant space so that the answer is partly tonic (in pitch content) and, at the same time, partly dominant (in registral position).

The study of elision in form class provides yet another case of one event/two opposite meanings: opening departures contained within ending goals. The overlap can be as brief as one beat on the phrase level or can involve whole segments as when development-section spillage into recapitulations creates a large-scale blurring or coalescence of major formal units, as in many sonata-form movements by Brahms (e.g., first movement of the Fourth Symphony). Recapitulations, in such cases, are often designed to emerge gradually even while the development is still winding down.

The "Sarabande" from Bach's French Suite No.2 illustrates a similar situation.

 

Figure 6. Bach, French Suite No. 2, Sarabande.

 

It reminds us that one of the best questions to use for exams, assignments, or class debate is one that begins "Argue in favor of two opposing interpretations of event X." In this piece, the question might be stated as follows: "Argue both of the following propositions: a) that the material at measure 17 is the beginning of a self-contained reprise section continuing to the end; and b) that the material at 17 is the second part of a reprise already started at 13." The mere asking of the question forces the student to confront an unusual number of basic analytical issues. That is, by considering alternatives, real thinking is guaranteed to take place. Potential clues would surely include, among others, the possibility of a given passage working in more than one way (e.g., the phrase at 13). In addition, matters of comparing second-section events with parallel constructions in the first section, matters of proportional balance in phrase and period structure, matters of tonal return vs. melodic return, and matters of varied melodic repetition would have to be considered.

The case of tonic restatement of opening material at the beginning of a sonata-form development is replete with triple opposing meanings involving location: the development section itself is, of course, one possibility; a deceptive repeat of the exposition another; and premature entry of the recapitulation yet another.

One paradox of illusion comes from the study of texture. Implied polyphony involves composing a single line to create an aural mirage of two or more melodic strands. The Gestalt principle of proximity grouping (often called the phi phenomenon) makes such a paradox possible just as it makes possible the appearance of constellations when we look at the stars. And we are all familiar with the extraordinarily ingenious creations from the Bach unaccompanied string literature. Similar examples can surface, however, in the music of other styles—if we are alert to the prospect (for example, in many of the remarkable jazz improvisations by vocalist Bobby McFerrin).

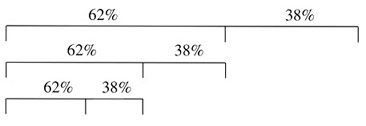
One final example involves the formal principle of "microcosm reflects the macrocosm," as in the infinite-regress paradox of looking into one mirror that is facing another. Golden-section proportional divisions of successively shorter temporal subsections provide a musical example as in Figure 7.

 

Figure 7. Golden Sections.

 

A humorous version of embedding is found in a story told about William James, who after having given a lecture on the solar system was approached by an old lady who claimed she had a superior theory to the one described by James.

"We don't live on a ball rotating around the sun," she said. "We live on a crust of earth on the back of a giant turtle."

Not wishing to demolish this absurd argument with the massive scientific evidence at his command, James decided to dissuade his opponent gently. "If your theory is correct, madam, what does this turtle stand on?"

"You're a very clever man, Mr. James, and that's a good question, but I can answer that. The first turtle stands on the back of a second, far larger, turtle."

"But what does this second turtle stand on?" James asked patiently.

The old lady crowed triumphantly. "It's no use, Mr. James—it's turtles all the way down."

It is commonplace in the teaching and textbooks of undergraduate theory to emphasize those aspects of musical structure and analysis that lend themselves to clear-cut right and wrong answers. This happens partly because the earliest phases of college training in music, which would likely focus mostly on fundamentals, do not often allow for subtle distinctions or interpretational nuance. It would be meaningless, for example, in freshman theory, to debate whether a D-major triad includes an 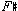or 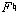. As a curriculum progresses beyond fundamentals, however, it is all too easy through insidious habit, to continue channeling learning patterns into safe, secure (yet narrow) grooves of compliance. An "answer-key" mentality can easily encroach on an entire theory program simply because less intellectual exertion is required to operate within all-or-nothing categories of cognition and hearing than to explore the gray shades of true musical exegesis.

At a beginning level of study, it is necessary, of course, to devote considerable time to establishing standards and conventions for the accurate collection and labeling of factual data. As training in both understanding and listening advances to successively higher levels of sophistication, though, many teachers are reluctant to deal with deception, irony, self-reference, duplicity, unrealized implication, double meanings, opposition of meanings, and dilemmas. In theory classes from about the junior level through advanced graduate seminars, circumstances abound for teaching about these processes—although the opportune moment may not always be seized. It is seldom recognized, however, that occasions for investigating these phenomena in freshman/sophomore theory are plentiful as well—that is, if the mind and ears are tuned to appreciate such possibilities.

My plea, then, is that musical understanding at all levels can be elevated and enhanced by paying more careful attention to the puzzling aspects of musical structure as well as to its more orderly, predictable, and well-behaved attributes. In fact, I think music can only be fully comprehended—so far as such a goal is possible—by acknowledging its wealth of internal contradictions and paradoxes. By reveling in this rich messiness instead of shying away from it, students can be led to a fuller aesthetic experience since such an approach forces them to encounter artistic issues of genuine significance. Explanations of details that seem baffling on the surface (i.e., lacking visible or obvious rational tidiness) can often be fathomed if tracked to a deeper level. Tying up these kinds of loose ends and, in the process, creating yet additional threads of inquiry at the next higher level of intellectual pursuit is at the core of "doing" music theory—and teaching it.

I stress the "doing" of theory (i.e., testing out ideas) as well as the "learning" of what others have discovered. Music theory, in this view, is not just a collection of factual information, but a creative act. Places to start are situations where one event means two things simultaneously (not just alternately), or where two different events have a shared or connected meaning, where a pat answer is contradicted by the context, or where special circumstances demand revising stereotypical responses. Quirks, deviations, aberrations, subterfuges, camouflages, idiosyncrasies, and vicious circles are not exceptions outside the normal flow of music—as they are often treated, when not skimmed over altogether; they are the music!

In addition, it should also be stressed that learning to hear and recognize such anomalies assumes that appropriate and powerful investigative concepts—including contradiction and paradox—are part of the filtering system through which sounds and thoughts are transformed into music. Such established schemata (i.e., frames of reference or cognitive scripts) permit the integration of stored knowledge in the brain with incoming data from the ears. Indeed such schemata make possible learning, memory, perception, inference, association, intuition, cued retrieval, analogy, and creativity. Just as adding a new word to our vocabulary often seems to make that word pop out ubiquitously for days afterward, regularly identifying antithetical elements in music will provide (through constructive brainwashing) the proper mental set for future recognition. Incorporating contradiction and paradox into the analytical arsenal considerably expands the range of explanatory options. There is nothing so dangerous in musical analysis as a single idea. As Abraham Maslow has said, "If a man's only tool is a hammer, he views every problem as a nail."

The importance of mental set can be dramatically illustrated with a short experiment. Let me quote a brief figurative passage that will sound like gibberish:

"With hocked gems financing him our hero bravely defied all scornful laughter that tried to prevent his scheme. Your eyes deceive, he had said; an egg not a table correctly typifies this unexplored planet. Now, three sturdy sisters sought proof forging along sometimes through calm vastness yet more often over turbulent peaks and valleys. Days became weeks, as many doubters spread fearful rumors about the edge. At last from nowhere welcome winged creatures appeared signifying momentous success."⁴

What is it all about? Although the words are familiar, it might as well be a foreign language. It seems as devoid of meaning as a complex middle-game board position would be to a novice at chess, or a triple-option wish-bone football diagram would be for someone outside of Oklahoma. And yet the passage becomes immediately clear through supplying a single cogent clue, much like a problematic musical passage might become suddenly comprehensible through application of the necessary conceptual framework. The magic filter for this language example is "Christopher Columbus discovering America." Now read the example again with this filter in place.

The ultimate merit of a pedagogical approach that filters in, rather than out, such messy topics as contradiction and paradox is a more vivid appreciation of aesthetic values—for example, structural values such as hierarchy, coherence, intricacy, cleverness, novelty, resistance; expressive values such as suspense, surprise, humor, drama, and poignancy; and contrasting paired values such as ambiguity/clarity, conflict/resolution, dynamism/stasis, growth/attenuation, profusion/economy. And finally, the true purpose of music theory—and theory pedagogy—can be distinguished not so much by the quality of answers provided but by which questions are worth asking in the first place.

---

¹Introductory material adapted from nationally syndicated column, "Looking at Language" by Richard Lederer.

²My thinking about this piece has been affected by Edgar Warren Williams, "In and About a Few Measures of Beethoven," 19th-Century Music (Fall 1983), 143-48.

³Adapted from an article by Robert J. Thornton in Chronicle of Higher Education.

⁴Quoted in W.R. Hartston and P.C. Wason, The Psychology of Chess (London: Batsford, 1983), 62.