A Primer for Atonal Set Theory1
Atonal set theory has a bad reputation. Like Schenkerian analysis in its earlier days, set theory has had an air of the secret society about it, with admission granted only to those who possess the magic password, a forbidding technical vocabulary bristling with expressions like "6-Z44" and "interval vector." It has thus often appeared to the uninitiated as the sterile application of arcane, mathematical concepts to inaudible and uninteresting musical relationships. This situation has created understandable frustration among musicians, and the frustration has grown as discussions of twentieth-century music in the professional theoretical literature have come to be expressed almost entirely in this unfamiliar language.
Where did this theory come from and how has it managed to become so dominant? Set theory emerged in response to the motivic and contextual nature of post-tonal music. Tonal music uses only a small number of referential sonorities (triads and seventh chords); post-tonal music presents an extraordinary variety of musical configurations. Tonal music shares a common practice of harmony and voice leading; post-tonal music is more highly self-referentialeach work defines anew its basic shapes and modes of progression. In tonal music, motivic relationships are constrained by the norms of tonal syntax; in post-tonal music, motives become independent and function as primary structural determinants. In this situation, a new music theory was needed, free of traditional tonal relationships and flexible enough to describe a wide range of new musical constructions. The structural novelties of post-tonal music caused theorists to rethink even the most basic elements of music, pitch and interval. On this new foundation, a new theory arose, flexible and powerful enough to describe a new musical world.
This new theory has its roots in work by Milton Babbitt, Allen Forte, David Lewin, Robert Morris, George Perle, and John Rahn, but it has flowered in many different directions.2 Set theory is not a single language, but a community of local dialects and subcultures. It is best understood not as a rigidly prescribed practice, but as an array of flexible tools for discovering and interpreting musical relationships. It should be emphasized that these relationships can and should be enjoyably audible. If set theory has occasionally veered into the inaudibly arcane, that should be blamed on the excesses of individual practitioners, not on the theory itself. At its best, the theory makes possible rich and interesting hearings of the finest musical works of the twentieth century.
Despite its occasionally forbidding appearance, atonal set theory is not particularly complicated, at least in its basic applications. No high-powered computers or advanced degrees in mathematics are needed—just a commitment to twentieth-century music, the ability to add and subtract small integers, and some good will. What follows is a primer of basic concepts of atonal set theory.
Octave Equivalence
There is something special about the octave. Pitches separated by one or more octaves are usually perceived as in some sense equivalent. Our musical notation reflects that equivalence by giving the same name to octave-related pitches. Since equivalence relationships underpin much of atonal set theory, it should be emphasized at the outset that equivalence does not mean identity. Example 1 shows two melodic lines from Schoenberg's String Quartet No. 4, one from the beginning of the first movement and one a few measures from the end.3
Example 1. Two equivalent melodies (Schoenberg, String Quartet No. 4, first movement).

Although the two lines differ in many ways, particularly in their range and rhythm, they are still understood as two different versions of one single underlying idea. In other words, they are equivalent.
In Example 2, the opening of Schoenberg's Piano Piece, Op. 11, No. 1, compare the first three notes of the melody with the sustained notes in measures 4-5.
Example 2. Two equivalent musical ideas (Schoenberg, Piano Piece, Op. 11, No. 1).

There are many differences between the two collections of notes (register, articulation, rhythm, etc.), but they sound equivalent because they both contain only a B, a  , and a G. As with other equivalences, the purpose of invoking octave equivalence is not to smooth out the variety of the musical surface, but to reveal the relationships that lie beneath the surface, lending unity and coherence to musical works.
, and a G. As with other equivalences, the purpose of invoking octave equivalence is not to smooth out the variety of the musical surface, but to reveal the relationships that lie beneath the surface, lending unity and coherence to musical works.
Pitch Class
It is useful to distinguish between a pitch (a tone with a certain frequency) and a pitch class (a group of pitches one or more octaves apart from one another). When we say that the lowest note on the cello is C, we are referring to a specific pitch. We can notate that pitch on the second ledger line beneath the bass staff. When we say that the tonic of Beethoven's Fifth Symphony is C, we are referring not to some particular pitch C, but to pitch-class C. Pitch-class C is an abstraction and cannot be accurately notated on musical staves. Sometimes, for convenience, a pitch class will be represented in musical notation, but, in reality, a pitch class is not a single thing; it is a class of things. A pitch and all the other pitches one or more octaves away from it are members of the same pitch class.
Enharmonic Equivalence
In common-practice tonal music,  is not equivalent to
is not equivalent to 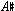 . Even on an equal-tempered instrument like the piano, the tonal system gives
. Even on an equal-tempered instrument like the piano, the tonal system gives  and
and 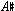 different functions. In G-major, for example,
different functions. In G-major, for example, 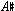 is
is 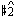 whereas
whereas  is
is 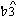 , and scale-degrees
, and scale-degrees 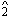 and
and 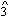 have very different musical roles. This distinction is largely abandoned in post-tonal music, where notes that are enharmonically equivalent are also functionally equivalent. Composers may occasionally notate pitches in what seems like a functional way (sharps for ascending and flats for descending, for example). For the most part, however, the notation is functionally meaningless, determined primarily by simple convenience and legibility.
have very different musical roles. This distinction is largely abandoned in post-tonal music, where notes that are enharmonically equivalent are also functionally equivalent. Composers may occasionally notate pitches in what seems like a functional way (sharps for ascending and flats for descending, for example). For the most part, however, the notation is functionally meaningless, determined primarily by simple convenience and legibility.
Integer Notation
Tonal music uses seven scale degrees or step classes. In C-major, for example, 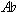 ,
, 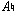 , and
, and 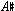 , in all octaves, are members of scale-degree
, in all octaves, are members of scale-degree 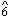 . Post-tonal music uses twelve pitch classes. All
. Post-tonal music uses twelve pitch classes. All 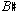 s,
s, 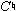 s, and
s, and 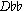 s are members of a single pitch class, as are all the
s are members of a single pitch class, as are all the  s and
s and 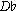 s, all the Cxs, Ds, and
s, all the Cxs, Ds, and 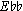 s, and so on. Our theoretical and analytical purposes are best served by cutting through the notational diversity and assigning integers from 0 through 11 to the twelve pitch classes. Set theory customarily uses a "fixed do" notation: The pitch class containing C,
s, and so on. Our theoretical and analytical purposes are best served by cutting through the notational diversity and assigning integers from 0 through 11 to the twelve pitch classes. Set theory customarily uses a "fixed do" notation: The pitch class containing C, 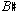 , and
, and 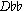 is arbitrarily assigned the integer 0;
is arbitrarily assigned the integer 0;  and
and 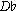 are members of pitch-class 1; D is a member of pitch-class 2; and so on.
are members of pitch-class 1; D is a member of pitch-class 2; and so on.
Integers are simple to grasp and to manipulate. They are traditional in music (as in figured bass numbers, for example) and useful for representing certain musical relationships. As long as we avoid committing the "numerological fallacy"—performing mathematical operations without regard to their musical implications—we will find them a great help.4 Set theory uses numbers to model musical relationships that are interesting and rewarding to hear. The theory and the music it describes are not, therefore, "mathematical" any more than our lives are "mathematical" just because we count our ages in integers.
Mod 12
Every pitch belongs to one of the twelve pitch classes. If you begin with a member of some pitch class, then go up or down one or more octaves, you arrive at another member of the same pitch class. In arithmetical terms, adding or subtracting 12 (or a multiple of 12) does not change pitch-class identity. Thus, 12 is a modulus, and set theory frequently relies upon arithmetic modulo 12, for which mod 12 is an abbreviation. In a mod 12 system, -12 = 0 = 12 = 24. Similarly, -13, -1, 23, and 35 are all equivalent to 11 (and to each other) because they are related to 11 (and to each other) by adding or subtracting 12 (or multiples of 12). It's just like telling time—twelve hours after four o'clock it's four o'clock again. Set theory sometimes uses negative numbers (for example, to suggest the idea of descending) and sometimes uses numbers larger than 11 (for example, to represent the distance between two widely separated pitches) but, in general, such numbers are discussed in terms of their mod 12 equivalents, from 0 to 11 inclusive.
Pitch Intervals
A theory of post-tonal music has no need to give different names to intervals with the same absolute size, such as diminished fourths and major thirds. In tonal music, such distinctions are functionally crucial. A third, for example, is an interval that spans three steps of a diatonic scale, while a fourth spans four steps. A major third is consonant while a diminished fourth is dissonant. In music that doesn't use diatonic scales and doesn't systematically distinguish between consonance and dissonance, it seems cumbersome and even misleading to use traditional interval names. It is easier and more accurate musically just to name intervals according to the number of semitones they contain. The intervals between C and E and between C and 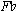 both contain four semitones and are both instances of interval 4, as are
both contain four semitones and are both instances of interval 4, as are 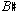 -
-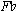 , C-Dx, and so on.
, C-Dx, and so on.
A pitch interval is simply the distance between two pitches, measured by the number of semitones between them. If we are concerned about the direction of the interval, whether it is ascending or descending, we can precede the number of semitones with either a plus sign (to indicate an ascending interval) or a minus sign (to indicate a descending interval). Intervals with a plus or minus sign are called directed or ordered intervals. If we are concerned only with the absolute space between two pitches (an unordered interval), we need only the number itself.
Whether an interval is considered ordered or unordered depends on our particular analytical interests at the time. Consider the melody by Webern given in Example 3.
Example 3. Motivic development via ordered pitch intervals (Webern, "Wie bin ich froh!" from Three Songs, Op. 25).

The intervallic ideas of its opening notes echo throughout the line. The ordered pitch intervals formed by its first three pitches occur again in two other places, in measure 2 (D-B- ) and measure 3 (C-A-
) and measure 3 (C-A- ). The second fragment spans a rest and helps to link two lines of the poem. The third one leaps up to a high
). The second fragment spans a rest and helps to link two lines of the poem. The third one leaps up to a high  , the highpoint of the melody and the last of the twelve pitch classes to be heard. These intervallic echoes, based on ordered pitch intervals are easy to hear.
, the highpoint of the melody and the last of the twelve pitch classes to be heard. These intervallic echoes, based on ordered pitch intervals are easy to hear.
The three melody notes at the beginning of the second measure,  -F-D, also relate to the opening three-note figure, but in a more subtle way: they have the same unordered pitch intervals (see Example 4).
-F-D, also relate to the opening three-note figure, but in a more subtle way: they have the same unordered pitch intervals (see Example 4).
Example 4. Motivic development via unordered pitch intervals.

The relationship is not as obvious as the one based on ordered pitch intervals, but it is still not hard to hear. The opening figure can thus be understood simultaneously in terms of its ordered and unordered pitch intervals. The ordered pitch intervals focus attention on the contour of the line, its balance of rising and falling motion. The unordered pitch intervals ignore contour and concentrate entirely on the spaces between the pitches.
Pitch-Class Intervals
A pitch-class interval is the distance between two pitch classes. Like pitch intervals, pitch-class intervals can be thought of either as ordered or unordered. To calculate an ordered pitch-class interval, envision the pitch classes arranged around a circular clockface and count clockwise (or envision a piano keyboard and count upward) from the first pitch class to the second. The ordered pitch-class interval from  to A, for example, is 8. Notice that the ordered pitch-class interval between A and
to A, for example, is 8. Notice that the ordered pitch-class interval between A and  (4) is different from that between
(4) is different from that between  and A (8). Excluding the unison, there are eleven different ordered pitch-class intervals.
and A (8). Excluding the unison, there are eleven different ordered pitch-class intervals.
In the Webern melody discussed above, the first four pitch classes are the same, in order, as the last four: G-E-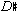 -
- (see Example 5).
(see Example 5).
Example 5. Different contour, but the same ordered pitch-class intervals.

The contours of the two fragments (their ordered pitch intervals) are different, but the ordered pitch-class intervals are the same: 9-11-3. This similarity is a nice way of rounding off the melodic phrase and of reinforcing the rhyme in the text: "Wie bin ich froh! . . . and leuchtet so!"
For unordered pitch-class intervals, direction no longer matters. All we care about now is the space between two pitch classes. Unordered pitch-class intervals are calculated from one pitch class to the other by the shortest available route, either up or down. The unordered pitch-class interval between  and A is 4, because it is only 4 semitones from any
and A is 4, because it is only 4 semitones from any  to the nearest available A. Notice that the unordered pitch-class interval between
to the nearest available A. Notice that the unordered pitch-class interval between  and A is the same as the unordered pitch-class interval between A and
and A is the same as the unordered pitch-class interval between A and  —4 in both cases. Excluding the unison, there are only six different unordered pitch-class intervals because, to get from one pitch class to any other pitch class, one never has to travel farther than six semitones.
—4 in both cases. Excluding the unison, there are only six different unordered pitch-class intervals because, to get from one pitch class to any other pitch class, one never has to travel farther than six semitones.
Let's return one more time to our Webern melody. We noted that the last four pitch classes were the same as the first four, but given a different contour. This change of contour makes something interesting happen: it puts the E up in a high register and groups the G, 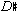 , and
, and  together in a low register. That registrally defined three-note collection (G-
together in a low register. That registrally defined three-note collection (G-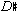 -
- ) contains unordered pitch-class intervals 1 (G-
) contains unordered pitch-class intervals 1 (G- ), 3 (
), 3 (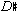 -
- ), and 4 (G-
), and 4 (G-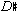 ). These are exactly the same as those formed by the first three notes of the figure (G-E-
). These are exactly the same as those formed by the first three notes of the figure (G-E-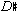 ): E-
): E- is 1, G-E is 3, and G-
is 1, G-E is 3, and G- is 4. The entire melody develops musical ideas from its opening figure, sometimes by imitating its ordered pitch intervals, sometimes by imitating its unordered pitch intervals, and sometimes, more subtly, by imitating its ordered or unordered pitch-class intervals (see Example 6).
is 4. The entire melody develops musical ideas from its opening figure, sometimes by imitating its ordered pitch intervals, sometimes by imitating its unordered pitch intervals, and sometimes, more subtly, by imitating its ordered or unordered pitch-class intervals (see Example 6).
Example 6. Development of the initial melodic figure.

An unordered pitch-class interval is also called an interval class. Just as each pitch-class contains many individual pitches, so each interval class contains many individual pitch intervals. A given pitch interval, its compounds, and its inversions with respect to the octave are members of the same interval class. Thus, for example, pitch intervals 23 (compound major seventh), 13 (minor ninth), 11 (major seventh), and 1 (semitone) are all members of interval-class 1.
We thus have four different ways of talking about intervals: ordered pitch interval, unordered pitch interval, ordered pitch-class interval, and unordered pitch-class interval. If, for example, we want to describe the interval from the lowest note in the Webern melody, B3, to the highest,  5, we can do so in four different ways. If we call it a +21, we have described it very specifically, conveying both the size of the interval and its direction. If we call it a 21, we express only its size. If we call it a 9, we have reduced a compound interval to its simple equivalent. If we call it a 3, we have expressed the interval in its simplest, most abstract form. None of these labels is better or more correct than the others. It's just that some are more concrete and specific while others are more general and abstract.
5, we can do so in four different ways. If we call it a +21, we have described it very specifically, conveying both the size of the interval and its direction. If we call it a 21, we express only its size. If we call it a 9, we have reduced a compound interval to its simple equivalent. If we call it a 3, we have expressed the interval in its simplest, most abstract form. None of these labels is better or more correct than the others. It's just that some are more concrete and specific while others are more general and abstract.
It's like describing any object in the world—what you see depends upon where you stand. If you stand a few inches away from a painting, for example, you may be aware of the subtlest details, right down to the individual brushstrokes. If you stand back a bit, you will be better able to see the larger shapes and the overall design. There is no single "right" place to stand; to appreciate the painting, you should be willing to move from place to place. One of the nice things about music is that you can hear a single object like an interval in many different ways at once, as though it were possible to stand in several different places at the same time.
Interval-Class Content
The sound of a sonority is determined to a significant degree by its interval-class content. This can be summarized in scoreboard fashion by indicating, in the appropriate column, the number of occurrences of each of the six interval classes. Example 7 refers again to the three-note sonority from Schoenberg's Piano Piece, Op. 11, No. 1.
Example 7. Interval-class content of a three-note sonority (Schoenberg, Piano Piece, Op. 11, No. 1).
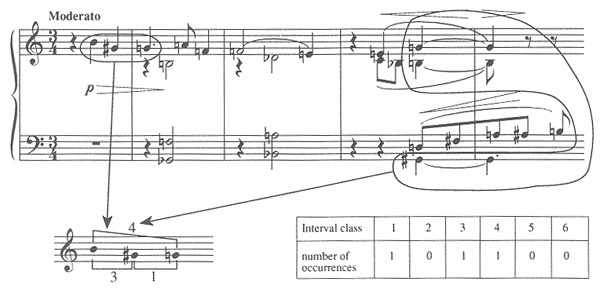
Like any three-note sonority, it necessarily contains three intervals—in this case one occurrence each of interval-classes 1, 3, and 4 (and no 2, 5, or 6). How different this is from the sonorities preferred by Stravinsky in the passage from his opera The Rake's Progress, labeled 1 and 2 in Example 8! These sonorities contain only 2s and 5s.
Example 8. Interval-class content of a contrasting three-note sonority (Stravinsky, The Rake's Progress, Act I, Scene 1).
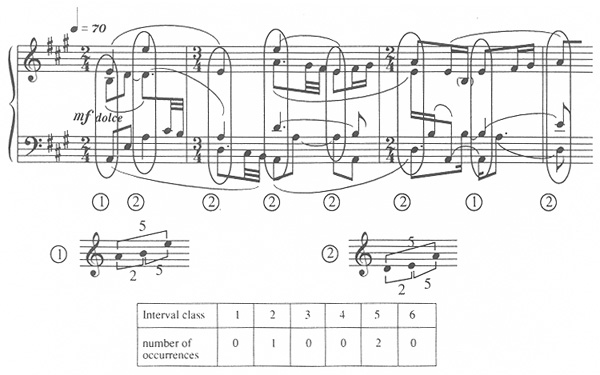
The interval-class content is usually presented as a string of six numbers with no spaces intervening. This is called an interval vector. The first number in an interval vector gives the number of occurrences of interval-class 1; the second number gives the number of occurrences of interval-class 2; and so on. The interval vector for the sonority in Example 7, G- -B, is 101100 and the interval vector for the sonorities in Example 8 (A-B-E and D-E-A) is 010020. Their difference in sound is clearly suggested by the difference in their interval vectors.
-B, is 101100 and the interval vector for the sonorities in Example 8 (A-B-E and D-E-A) is 010020. Their difference in sound is clearly suggested by the difference in their interval vectors.
Interval vectors can be constructed for sonorities of any size or shape. Interval vectors are not really necessary for talking about traditional tonal music. There, only a few basic sonorities—four kinds of triads and five kinds of seventh chords—are regularly in use. Post-tonal music, however, confronts us with a huge variety of musical sonorities. The interval vector is a convenient way of summarizing their basic sound.
Even though the interval vector is not as necessary a tool for tonal music as for post-tonal music, it can offer an interesting perspective on traditional formations. Example 9 calculates the interval vector for the major scale.
Example 9. Interval Vector for the major scale.

Notice the methodical process of extracting each interval class. First, the intervals formed with the first note are extracted, then those formed with the second note, and so on. As with any seven-note collection, there are 21 intervals in all.
Certain intervallic properties of the major scale are immediately apparent from its interval vector. It has only one tritone (fewer than any other interval) and 6 occurrences (more than any other interval) of interval-class 5 which contains the perfect fourth and fifth. This probably only confirms what we already knew about this scale, but the interval vector makes the same kind of information available about less familiar collections. The interval vector of the major scale has another interesting property—it contains a different number of occurrences of each of the interval classes. This is an extremely important and rare property (only three other collections have it), and it makes possible the traditional tonal hierarchy of closely and distantly related keys. In comparison to the unique multiplicity of interval classes in the major scale, the interval vector for the whole-tone scale—060603—presents a stark either/or. The contrasting properties of the two scales are suggested by their contrasting interval vectors.
Pitch-Class Sets
Pitch-class sets are the basic building blocks of much post-tonal music. A pitch-class set is simply an unordered collection of pitch-classes. It is like a motive without many of its customary identifying characteristics—register, rhythm, and order. Example 10 shows five different occurrences of a single pitch-class set, [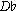 , E, F, G], in the Gavotte from Schoenberg's Suite for Piano, Op. 25.
, E, F, G], in the Gavotte from Schoenberg's Suite for Piano, Op. 25.
Example 10. A single pitch-class set expressed in five different ways (Schoenberg, Gavotte, from Suite for Piano, Op. 25).

It is expressed in a variety of ways, but always retains its basic pitch-class and interval-class identity. A balance of compositional unity and diversity can be achieved by selecting a pitch-class set (or a small number of different pitch-class sets) as a basic structural unit, and then transforming that basic unit in various ways. When we listen to or analyze music, we search for coherence. In a great deal of post-tonal music, that coherence is determined by the use of pitch-class sets.
Normal Form
A pitch-class set can be presented musically in a variety of ways. Conversely, many different musical figures can represent the same pitch-class set. To aid in recognizing a pitch-class set no matter how it is presented in the music, it is often helpful to put it into a simple, compact, easily grasped form called the normal form.5 The normal form—the most compressed way of writing a pitch-class set—makes it easy to see the essential attributes of a sonority and to compare it to other sonorities.
The normal form of a pitch-class set is similar to the root position of a triad, in that both are simple, compressed ways of representing sonorities that can occur in many positions and spacings. There are important differences however. In traditional tonal theory, the inversions of a triad are generated from the relatively more stable root position. The normal form, in contrast, has no particular stability or priority. It is just a convenient way of writing sets so that they can be more easily studied and compared.
To put a set in normal form, its pitch classes must be arranged in ascending order, within an octave, with the smallest possible interval between the first and last notes, and with the smaller intervals packed toward the bottom.6 For most sets, the normal form is evident from simple inspection, but here is the step-by-step procedure:
1. Excluding doublings, write the pitch classes ascending within an octave. There will be as many different ways of doing this as there are pitch classes in the set, since an ordering can begin on any of the pitch classes in the set. (The set from Schoenberg's Gavotte, for example, can be written out as E-F-G-
, F-G-
-E, G-
-E-F, and
-E-F-G).
2. Choose the ordering which has the smallest interval from the lowest to the highest note. (The normal form of the set from Schoenberg's Gavotte is [
, E, F, G]—the interval from
to G is only 6).
3. If two or more orderings share the same smallest interval from the lowest to the highest note, choose the ordering that is most packed to the left. To determine which is most packed to the left, compare the intervals between the first and second-to-last notes. If the determination is still not clear, compare the intervals between first and third-to-last notes, and so on. (For example, the famous "changing chord" from Schoenberg's Five Orchestral Pieces, Op. 16, No. 3, can be written in two ways with only an 8 from lowest to highest: E-
-A-B-C and
-A-B-C-E. Of these, [
, A, B, C, E] is the normal form, since it has the smaller interval from first to second-to-last).
4. If all of the comparisons of Rule 3 still produce no clear choice, then arbitrarily pick the ordering beginning with the pitch class represented by the smallest integer. (For example, A-
-F,
-F-A, and F-A-
are in a three-way tie according to Rule 3. [
, F, A] is designated as the normal form since its first pitch class is 1, which is lower than 5 or 9.)
Transposition
The term transposition traditionally refers to lines of pitches. When we transpose a tune from C major to G major, we transpose each pitch, in order, by some pitch interval. This operation preserves the ordered pitch intervals in the line and thus its contour. Because contour is such a basic musical feature, it is easy to recognize when two lines of pitches are related by transposition.
Transposing a set (not a line) of pitch classes (not pitches) is somewhat different. To transpose a pitch-class set by some interval n, an operation represented by the expression Tn, simply add n to each pitch class in the set. For example, to transpose [5, 7, 8, 11] by pitch-class interval 8, simply add 8 (mod 12) to each element in the set to create a new set [1, 3, 4, 7]. If the first set is in normal form, its transposition will be also (with a small number of exceptions related to the fourth rule for determining normal form).
A pitch-class set is a collection with no specified order or contour. As a result, transposition of a set preserves neither order nor contour. The four pitch-class sets circled in Example 11 are all transpositions of one another.
Example 11. Transpositionally equivalent pitch-class sets (Webern, Concerto for Nine Instruments, op. 24, second movement).

These sets are dissimilar in many obvious ways, including their pitch and pitch-class content, their manner of presentation, their contour, and their order. With all of these differences, they still have two important things in common. First, they contain one-to-one correspondences among their elements. This is particularly clear when the sets are written in normal form, as they are beneath the score in Example 11. For example, the 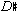 has the same position in the first set that the D has in the second set, the B in the third set, and the
has the same position in the first set that the D has in the second set, the B in the third set, and the 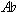 in the fourth set. Second, they all have the same interval vector; each of them contains interval-classes 1, 3, and 4, and no others. This gives them a similar sound. Transposition of a set of pitch classes may change many things, but it preserves interval-class content. Along with inversion, transposition is one of only two operations that do so, and consequently, is an important compositional means of creating a deeper unity beneath a complex musical surface. Consider the beginning of the piano introduction to one of the songs from Schoenberg's Book of the Hanging Gardens, Op. 15, shown in Example 12.
in the fourth set. Second, they all have the same interval vector; each of them contains interval-classes 1, 3, and 4, and no others. This gives them a similar sound. Transposition of a set of pitch classes may change many things, but it preserves interval-class content. Along with inversion, transposition is one of only two operations that do so, and consequently, is an important compositional means of creating a deeper unity beneath a complex musical surface. Consider the beginning of the piano introduction to one of the songs from Schoenberg's Book of the Hanging Gardens, Op. 15, shown in Example 12.
Example 12. Transpositionally equivalent pitch-class sets, and a transpositional path (Schoenberg, Book of the Hanging Gardens, Op. 15, No. 11).

The opening four-note melody in the right hand of the piano describes a certain pitch-class set, [ ,
, 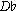 , D, F] in normal form. When the music continues in measure 2, the right hand of the piano transposes [
, D, F] in normal form. When the music continues in measure 2, the right hand of the piano transposes [ ,
, 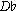 , D, F] to T3, resulting in [
, D, F] to T3, resulting in [ , E, F,
, E, F,  ]. Then, in measure 4, it transposes again, this time to T7, resulting in [F,
]. Then, in measure 4, it transposes again, this time to T7, resulting in [F,  , A, C]. The music thus takes an initial musical idea and projects it through a transpositional path: T0-T3-T7. That succession of transposition levels, 0-3-7, exactly mirrors the intervallic succession of the first three notes of the melody,
, A, C]. The music thus takes an initial musical idea and projects it through a transpositional path: T0-T3-T7. That succession of transposition levels, 0-3-7, exactly mirrors the intervallic succession of the first three notes of the melody,  -
-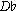 -F. The passage is thus audibly unified, not only by the transpositional equivalence of three pitch class sets, but by its large-scale reproduction of a small-scale motivic idea.7
-F. The passage is thus audibly unified, not only by the transpositional equivalence of three pitch class sets, but by its large-scale reproduction of a small-scale motivic idea.7
Inversion
Like transposition, inversion is an operation traditionally applied to lines of pitches. In inverting a line of pitches, order is preserved and contour is reversed—each ascending pitch interval is replaced by a descending one and vice versa. Furthermore, traditional tonal practice requires only that interval sizes be maintained, not interval qualities (major can become minor, and vice versa).
Inversion of a pitch-class set is a bit different. It is best understood as a compound operation expressed as TnI, where "I" means "invert" and "Tn" means "transpose by some interval n." By convention, we will always invert first and then transpose. The inversion of pitch-class n is 12-n. Pitch-class 1 inverts to -1, or 11. 2 inverts to 10; 3 inverts to 9; and so on. After we invert, we will transpose in the usual way.
Example 13 shows again the opening of Schoenberg's Piano Piece, Op. 11, No. 1.
Example 13. Inversionally equivalent pitch-class sets.

Compare the first two sets circled in the example. They have the same interval-class content, but their intervals are arranged in reverse order. The second set has the same intervals reading from the top down as the first does reading from the bottom up. Sets related by inversion can always be written in this way. Now compare the first and third sets. Again, these two sets are related by inversion. They have the same interval-class content, but the intervals are in reverse order.
To invert a set, simply invert each member of the set in turn. For example, to apply the operation T5I to the set [1, 3, 4, 7], just apply T5I to each integer in turn. Remembering to invert before transposing, we get ((12-1)+5, (12-3)+5, (12-4)+5, (12-7)+5) = (4, 2, 1, 10). Notice that if we write this new set in reverse order [10, 1, 2, 4] it will be in normal form. There will be some exceptions, but generally when you invert a set in normal form, the resulting set will be in normal form written backwards.
The concept of index number offers a simpler way both of inverting sets and of telling if two sets are inversionally related.8 When we compared transpositionally related sets, we subtracted corresponding elements in each set and called that difference the "transposition number." When comparing inversionally related sets, we will add corresponding elements and call that sum an "index number." When two sets are related by transposition and both sets are in normal form, the first element in one set corresponds to the first element in the other, the second to the second, and so on. When two sets are related by inversion and both are in normal form, the first element in one set will usually correspond to the last element in the other, the second to the second-to-last, and so on. This is because inversionally related sets are mirror images of each other.
Here again are the first and third sets from Example 13, written in integer notation: [7, 8, 11] and [6, 9, 10]. If we add the pairs of corresponding elements (first to last, second to second-to-last, and last to first), we get 5 (mod 12) in each case. These two sets are related at T5I. Any two sets in which the corresponding elements all have the same sum are related by inversion and that sum is the index number. To find the index number for two inversionally related pitch classes, simply add them together. Conversely, to perform the operation TnI on some pitch class, simply subtract it from n. To perform the operation T4I on [10, 1, 2, 6], for example, subtract each element in turn from 4: (4-10, 4-1, 4-2, 4-6) = (6, 3, 2, 10). As before, inverting a set in normal form produces the normal form of a new set written backwards. The normal form of (6, 3, 2, 10) is [10, 2, 3, 6].
Set Class
Consider the following collection of pitch-class sets, all given in normal form.
[2, 5, 6]
[3, 6, 7]
[4, 7, 8]
[5, 8, 9]
[6, 9, 10]
[7, 10, 11]
[8, 11, 0]
[9, 0, 1]
[10, 1, 2]
[11, 2, 3]
[0, 3, 4]
[1, 4, 5][6, 7, 10]
[7, 8, 11]
[8, 9, 0]
[9, 10, 1]
[10, 11, 2]
[11, 0, 3]
[0, 1, 4]
[1, 2, 5]
[2, 3, 6]
[3, 4, 7]
[4, 5, 8]
[5, 6, 9]
In the first column, the first entry is an arbitrarily chosen set which is transposed at each of the twelve transposition levels. Each of the twelve sets is related to the remaining eleven by transposition. The second column begins with an inversion of the set, which is similarly transposed at each of the twelve levels. In the second column, as in the first, each pitch-class set is related by transposition to the other eleven. Now consider all twenty-four of these sets together. Each of the twenty-four is related to all of the others by either transposition or inversion. The twenty-four pitch-class sets thus comprise a single, closely related family of sets called a set class. Each pitch-class set is a member of the set-class.
Just as a pitch class contains many equivalent pitches and an interval class contains many equivalent intervals, a set class contains many equivalent sets. Normally, a set class contains twenty-four members. A set class containing symmetrical sets, however, has fewer. The set class of the diminished-seventh chord, for example, contains only three distinct members: [ , E, G,
, E, G,  ], [D, F,
], [D, F, 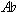 , B], and [C,
, B], and [C, 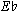 ,
,  , A]. Few sets are as redundant as this one (although one set, the whole-tone scale, is even more so). Most set classes contain twenty-four members; the rest have between two and twenty-four.
, A]. Few sets are as redundant as this one (although one set, the whole-tone scale, is even more so). Most set classes contain twenty-four members; the rest have between two and twenty-four.
Set-class membership is an important part of post-tonal musical structure. Every pitch-class set belongs to a single set class. The sets in a set class are all related to each other by either Tn or TnI. As a result, they all have the same interval-class content. By using members of a single set class in a composition, a composer can create underlying coherence while varying the musical surface.
Let's look yet again at the opening section of Schoenberg's Piano Piece, Op. 11, No. 1 to see how set-class membership can lend musical coherence to a varied surface. The passage (omitting the brief varied repetitions in measures 5-8) is shown in Example 14 with a number of pitch-class sets circled or joined by a beam. All of these pitch-class sets are members of the same set class.
Example 14. Varied presentation of members of a single-set class.
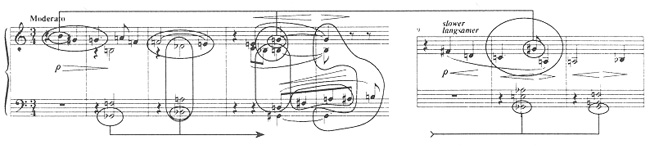
In the first three measures, a single continuous melody descends from its highpoint on B. In measures 4-5, the melody is reduced to a two-note fragment that reaches up to G (two immediate repetitions of this figure are omitted from the example). In measures 9-11, the opening melody returns in a varied form with a highpoint of  . These three notes, B-G-
. These three notes, B-G- , are separated in time but associated as contour highpoints. These are the same pitch classes as the first three notes of the piece and the sustained notes in measures 4-5.
, are separated in time but associated as contour highpoints. These are the same pitch classes as the first three notes of the piece and the sustained notes in measures 4-5.
Each note in this large-scale statement is also part of at least one small-scale statement of another member of the same set class. The B in measure 1 is part of the collection [G,  , B]. In measures 4-5, the highpoint G is part of not only the sustained chord [G,
, B]. In measures 4-5, the highpoint G is part of not only the sustained chord [G,  , B] but also part of the registral grouping [G,
, B] but also part of the registral grouping [G,  , B]. An additional member of the set class, [
, B]. An additional member of the set class, [ , B, D], is formed in the middle of the texture and still another, [
, B, D], is formed in the middle of the texture and still another, [ , A,
, A,  ], is formed by the moving part in the tenor voice. In measure 10, the
], is formed by the moving part in the tenor voice. In measure 10, the  is part of the collection [
is part of the collection [ , A, C]. Additional members of the set class are sprinkled throughout the passage. In measure 3, for example, both the left-hand chord and the highest three notes in the measure are members of the set class. The passage as a whole is also spanned by a large-scale statement in the bass. The chords in measures 2-3 present
, A, C]. Additional members of the set class are sprinkled throughout the passage. In measure 3, for example, both the left-hand chord and the highest three notes in the measure are members of the set class. The passage as a whole is also spanned by a large-scale statement in the bass. The chords in measures 2-3 present  -
- in the bass. When the chords return in measures 10-11, the
in the bass. When the chords return in measures 10-11, the  is restated, then G arrives to complete the set-statement, [
is restated, then G arrives to complete the set-statement, [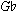 , G,
, G,  ].
].
The passage is virtually saturated with occurrences of this set class. It occurs as a melodic fragment, as a chord, and as a combination of melody and chord. It is articulated by register and, over a large span, by contour and mode of attack. An entire network of musical associations radiates from the opening three-note melodic figure. Some of the later statements have the same pitch content, some the same pitch-class content. Some are related by transposition, some by inversion. All are members of the same set class. As in tonal music, but with even greater intensity, an initial musical idea grows and develops as the music proceeds.9
Prime Form
There are two standard ways of naming set classes. First, Allen Forte, has compiled a well-known list of set classes. He identifies each with a pair of numbers separated by a dash (for example, 3-4). The number before the dash tells the number of pitch classes in the set. The number after the dash gives its position on Forte's list. Set-class 3-4, for example, is the fourth on Forte's list of three-note set classes. Forte's names are widely used.
The second common way of identifying set classes is to look at all of the members of the set class, select the one with the "most normal" of normal forms, and use that to name the set-class as a whole. This optimal form, called the prime form, begins with 0 and is most packed to the left. Of the twenty-four pitch-class sets listed at the beginning of the previous section of this article, two begin with 0: 034 and 014. Of these, (014) is the most packed to the left and is the prime form. Those twenty-four sets are all members of the set class with prime form (014). More familiarly, we say that each of those sets "is a (014)." In the rest of this article, set classes will be identified by both their name according to Forte and, in parentheses, their prime form.10
Here is the procedure for finding the prime form of a set class, a process usually referred to as putting a set in prime form:
- Put the set into normal form. (Take [1, 5, 6, 7] as an example.)
- Transpose the set so that the first element is 0. (If we transpose [1, 5, 6, 7] by T11, we get [0, 4, 5, 6].)
- Invert the set and repeat steps 1 and 2. ([l, 5, 6, 7] inverts to (11, 7, 6, 5). The normal form of that set is [5, 6, 7, 11]. If that set is transposed at T7, the result is [0, 1, 2, 6].)
- Compare the results of step 2 and step 3; whichever is more packed to the left is the prime form. ([0, 1, 2, 6] is more packed to the left than [0, 4, 5, 6], so (0126) is the prime form of the set class of which [1, 5, 6, 7], our example, is a member.)
Lists of set classes are available in many published works, including the books by Forte, Rahn, and Morris cited in the notes to this article. Considering the large number of pitch class sets, there are surprisingly few set classes. For example, there are 220 distinct trichords, but these can be grouped into just twelve different trichord-classes. There are also only twelve nonachord-classes. Similarly, there are only 29 tetrachord-cIasses and octachord-classes, 38 pentachord-classes and septachord-classes, and 50 hexachord-classes.
At this very basic level, set theory involves naming things, finding precise, accurate, and consistent ways of describing musical objects. While naming things may be a low-level analytical act, it is an indispensable first step toward musical understanding. Like Adam in the Garden of Eden, we find ourselves in a new world and, just as his first task was to name all the beasts of the field and fowl of the air, ours has been to develop a flexible, accurate nomenclature for notes, intervals, and collections. A reliable music theory must not stop there, but it must certainly start there.
Z-relation
Any two sets related by transposition or inversion must have the same interval-class content. The converse, however, is not true. There are pairs of sets (one pair of tetrachords, three pairs of pentachords, and fifteen pairs of hexachords) that have the same interval-class content, but are not related to each other by either transposition or inversion and thus are not members of the same set class. Sets that have the same interval content but are not transpositions or inversions of each other are Z-related and the relationship between them is the Z-relation (the Z doesn't stand for anything in particular).11 Sets in the Z-relation will sound similar because they have the same interval-class content, but they won't be as closely related to each other as sets that are members of the same set class. If the members of a set class are like siblings within a tightly knit nuclear family, then Z-related sets are like first cousins. In Example 15, an excerpt from the third of Stravinsky's Pieces for String Quartet, the occurrences of 4-Z15 (0146) in measures 24-26 are strongly linked to the similar occurrences of 4-Z29 (0137) in measures 27-28.
Example 15. The Z-relation (Stravinsky, Pieces for String Quartet, No. 3).

Any set with a Z in its name has a "Z-correspondent," another set with a different prime form but the same interval vector. On most set lists, the Z-related hexachords are listed across from one another, but you will have to look through the list for the Z-related sets of other sizes.
Complement Relation
For any set, the pitch classes it excludes constitute its complement. The complement of the set [3, 6, 7], for example, is [8, 9, 10, 11, 0, 1, 2, 4, 5]. Any set and its complement, taken together, will contain all twelve pitch classes. For any set containing n elements, its complement will contain 12-n elements.
There is an important intervallic similarity between a set and its complement. It might seem logical to suppose that whatever intervals a set has in abundance, its complement will have few of, and vice versa. It turns out, however, that a set and its complement always have a similar distribution of intervals. For complementary sets, the difference in the number of occurrences of each interval is equal to the difference in the size of the sets (except for the tritone, where it will be half that difference).12 If a tetrachord has the interval vector 021030, its eight-note complement will have the vector 465472. The eight-note set has four more of everything (except for the tritone of which it has two more). The larger set is like an expanded version of its smaller complement.
This intervallic relationship holds even if the two sets are not literally complements of each other, so long as they are members of complement-related set classes. For example, [3, 4, 5] and [5, 6, 7, 8, 9, 10, 11, 0, 1] are not literal complements of each other, since they share pitch-class 5. However, they are members of complement-related set classes. In other words, each set is related by transposition or inversion to the literal complement of the other, and therefore they have a similar distribution of intervals. Complement-related sets do not have as much in common as transpositionally or inversionally related sets, but they do have a similar sound because of the similarity of their interval content.
The complement relation is particularly important in any music in which the twelve pitch classes are circulating relatively freely and in which the aggregate (a collection containing all twelve pitch classes) is an important structural unit. Whenever the aggregate is divided into two parts, each part will have a similar distribution of intervals. If, for example, five of the pitch classes are played as a melody and the remaining seven are played in accompanying chords, the melody and the accompaniment will have a similar sound because they contain a similar distribution of intervals.
The final four-note chord of Schoenberg's Little Piano Piece, Op. 19, No. 2 is a form of 4-19 (0148), a set class prominent throughout that piece and one common in much of Schoenberg's music (see Example 16).
Example 16. The complement relation (Schoenberg, Little Piano Piece, Op. 19, No. 2).

The last eight notes of the piece (which, of course, include that final four-note chord), are a form of 8-19 (01245689), the complementary set class. Compare the interval vectors of these two sets: the vector for 4-19 is 101310 and the vector for 8-19 is 545752. Both sets are particularly rich in interval-class 4. In fact, no four- or eight-note set contains more 4s than these do. And notice how prominently the 4s are featured in the music. Because of the complement relation, the final four-note chord sounds similar to the larger eight-note collection of which it is a part. Most lists of sets place complement-related sets across from one another. In Forte's set names, complementary sets always have the same number following the dash. Thus, 4-19 and 8-19 are complements of each other as are 3-6 and 9-6, 5-Z12 and 7-Z12, and so on.
The complement relationship holds particular interest for hexachords. Some hexachords are "self-complementary"—they and their complements are members of the same set class. For a simple example, consider the hexachord [2, 3, 4, 5, 6, 7]. Its complement is [8, 9, 10, 11, 0, 1]. But both of these sets are members of set-class 6-1 (0123456). In other words, self-complementary hexachords are those that are related to their complements by either Tn or TnI.
If a hexachord is not self-complementary, then it must be Z-related to its complement. Remember that with complementary sets, the difference in the number of occurrences of any interval is equal to the difference in the size of the two sets. But a hexachord is exactly the same size as its complement. As a result, a hexachord always has exactly the same interval content as its complement. If it is also related to its complement by Tn or TnI, then it is self-complementary. If not, then it is Z-related to its complement. This intervallic relationship between complementary hexachords is particularly important for much twelve-tone music.
In addition to the basic nomenclature and relationships described above, atonal set theory has developed a relatively sophisticated vocabulary for discussing common tones under transposition and inversion;13 the similarity of non-equivalent sets14 inversional symmetry and axes of symmetry,15 subset and superset relations,16 and ways of grouping set classes into interrelated complexes.17 Despite this sophistication, post-tonal theory is still in its relative infancy, particularly compared to tonal theory, now entering at least its fourth century of development. That offers both bad news and good news to those eager to understand post-tonal music. The bad news is that we are still at a relatively primitive analytical stage, with considerable effort still devoted to comparatively rudimentary analytical acts, like taking an inventory of harmonic vocabulary or describing motivic structure. Of course, there is more to music (and should be more to music analysis) than harmonic and motivic structure. The good news is that in recent years, set theory has begun to branch out into voice leading,18 rhythm,19 contour,20 and timbre.21 As crucial as these topics are to a complete understanding of post-tonal music, they have had to await the prior construction of a secure theory of pitch organization. Now that a reliable theory of pitch organization is in place, a rapid expansion into other musical areas has become not only possible, but an exciting fact of current post-tonal theory.
1This article is adapted from my Introduction to Post-Tonal Theory, an undergraduate textbook recently published by Prentice-Hall.
2A complete, annotated bibliography of post-tonal theory, compiled by Martha Hyde and Andrew Mead, may be found in Music Theory Spectrum 11/1 (1989): 44-48. The field as a whole originates with Milton Babbitt's influential articles and teaching, particularly "Some Aspects of Twelve Tone Composition," The Score and I.M.A. Magazine 12 (1955): 53-61; "Twelve-Tone Invariants as Compositional Determinants," Musical Quarterly 46 (1960): 246-59; "Set Structure as a Compositional Determinant," Journal of Music Theory 5/2 (1961): 72-94. Although these articles focus on twelve-tone music, their theoretical categories have broad application in post-tonal music. Some of Babbitt's central concerns are presented more informally in Milton Babbitt: Words About Music, eds. Stephen Dembski and Joseph N. Straus (Madison: University of Wisconsin Press, 1987). The basic concepts presented in this article are drawn from Babbitt's work, and also from three widely used books: Allen Forte, The Structure of Atonal Music (New Haven: Yale University Press, 1973); John Rahn, Basic Atonal Theory (New York: Longman, 1980); and George Perle, Serial Composition and Atonality, 5th ed. (Berkeley: University of California Press, 1981). Two important recent books offer profound new perspectives on this basic material, and much else besides: David Lewin, Generalized Musical Intervals and Transformations (New Haven: Yale University Press, 1987); Robert Morris, Composition with Pitch Classes (New Haven: Yale University Press, 1987).
3Although atonal set theory is most closely associated with the "free atonal" music of Schoenberg, Webern, and Berg, it has much more general applications throughout the range of post-tonal music, including particularly twelve-tone serial music.
4See Rahn, Basic Atonal Theory, 19, for a related discussion of the numerological fallacy.
5The concept of "normal form" is original with Milton Babbitt. See "Set Structure as a Compositional Determinant."
6Allen Forte (The Structure of Atonal Music) and John Rahn (Basic Atonal Theory) differ slightly in their definition of normal form, but this results in only a small number of discrepancies. This article adopts Rahn's formulation. Unfortunately, many different notational conventions are currently in use. In this article, normal forms will be given in square brackets.
7The eleventh song from Schoenberg's Book of the Hanging Gardens has been analyzed briefly by Tom Demske ["Registral Centers of Balance in Atonal Works by Schoenberg and Webern," In Theory Only 9/2-3 (1986): 60-76], and, in great and compelling detail by David Lewin ["Toward the Analysis of a Schoenberg Song (Op. 15, No. 11)," Perspectives of New Music 12/1-2 (1973-4): 43-86]. My brief discussion is indebted to the latter.
8The concept of "index number" was first discussed by Milton Babbitt in "Twelve-Tone Rhythmic Structure and the Electronic Medium," Perspectives of New Music 1/1 (1962): 49-79; reprinted in Perspectives on Contemporary Music Theory, eds. Boretz and Cone (New York: Norton, 1972), 148-79. He developed this concept in many of his articles, including "Contemporary Music Composition and Music Theory as Contemporary Intellectual History," Perspectives in Musicology, eds. Brook, Downes, and Van Solkema (New York: Norton, 1971), 151-84.
9Schoenberg's Piano Piece, Op. 11, No. 1, has been widely analyzed. George Perle discusses its intensive use of this same three-note motive (which he calls a "basic cell") in Serial Composition and Atonality. See also Allen Forte, "The Magical Kaleidoscope: Schoenberg's First Atonal Master work, Opus 11, No. 1," Journal of the Arnold Schoenberg Institute 5 (1981): 127-68; and Gary Wittlich, "Intervallic Set Structure in Schoenberg's Op. 11, No. 1," Perspectives of New Music 13 (1972): 41-55.
10As with normal form, conventions for notating prime forms vary from source to source.
11The Z-relationship was first described by David Lewin in "The Intervallic Content of a Collection of Notes, Intervallic Relations between a Collection of Notes and Its Complement: An Application to Schoenberg's Hexachordal Pieces," Journal of Music Theory 4 (1960): 98-101. The use of the label "Z" to refer to this relationship is a coinage of Allen Forte's (see The Structure of Atonal Music, 21-24).
12The intervallic relationship of complementary sets was first discovered by Milton Babbitt with regard to hexachords. Generalizing this relationship to sets of other sizes, was the work of Babbitt and David Lewin (see Lewin's "The Intervallic Content of a Collection of Notes"). Babbitt discusses the development of his theorem about hexachords and its subsequent generalization in Milton Babbitt: Words About Music, 104-106.
13Common tones under transposition and inversion are discussed in Forte, The Structure of Atonal Music, 29-46 and Rahn, Basic Atonal Theory, 97-115. For Morris's approach to the question, usually through the use of matrices, see his review of Rahn, Basic Atonal Theory in Music Theory Spectrum 4 (1982): 138-55 and his own Composition with Pitch Classes, 70-78. Lewin describes the same phenomena in terms of his Embedding and Injection Functions. See Generalized Musical Intervals, 88-156.
14On similarity relations, see Allen Forte, The Structure of Atonal Music, 46-59; Charles Lord, "Intervallic Similarity Relations in Atonal Set Analysis," Journal of Music Theory 25 (1981): 91-111; Robert Morris, "A Similarity Index for Pitch-Class Sets," Perspectives of New Music 18/1-2 (1979-80), 445-60; John Rahn, "Relating Sets," Perspectives of New Music 18/1-2 (1979-80): 483-98; and David Lewin, "A Response to a Response: On PC Set Relatedness," Perspectives of New Music 18/1-2 (1979-80): 498-502.
15On inversional symmetry and its musical consequences, see Rahn, Basic Atonal Theory, 49-51 and 91-95; Lewin, "Inversional Balance as an Organizing Force in Schoenberg's Music and Thought," Perspectives of New Music 6/2 (1968): 1-21; and Perle, Twelve-Tone Tonality (Berkeley: University of California Press, 1977).
16Subset and superset relations are discussed in Forte, The Structure of Atonal Music, 24-29 and Rahn, Basic Atonal Theory, 115-117.
17Forte's K and Kh relations are the best known models of set complexes. He has recently evolved a new model in "Pitch-Class Set Genera and the Origin of Modern Harmonic Species," Journal of Music Theory 32/2 (1988): 187-270.
18See Alan Chapman, "Some Intervallic Aspects of Pitch-Class Set Relations," Journal of Music Theory 25 (1981): 275-90; Allen Forte, "New Approaches to the Linear Analysis of Music," Journal of the American Musicological Society 41 (1988): 315-48; Christopher Hasty, "On the Problem of Succession and Continuity in Twentieth-Century Music," Music Theory Spectrum 8 (1986): 58-74. See also two important recent dissertations: John Roeder, "A Theory of Voice-Leading for Atonal Music" (Yale University, 1984) and Henry Klumpenhouwer, "A Generalized Model of Voice-Leading for Atonal Music" (Harvard University, 1991).
19See David Lewin, Generalized Musical Intervals, particularly 22-30 and 60-87; Allen Forte, "Aspects of Rhythm in Webern's Atonal Music," Music Theory Spectrum 2 (1980): 90-109; Allen Forte, "Foreground Rhythm in Early Twentieth-Century Music," Music Analysis 2/3 (1983): 239-68; Martha Hyde, "A Theory of Twelve-Tone Meter," Music Theory Spectrum 6 (1984): 63-78; Christopher Hasty, "Rhythm in Post-Tonal Music: Preliminary Questions of Duration and Motion," Journal of Music Theory 25 (1981): 183-216.
20See Morris, Composition with Pitch Classes, 23-33; Michael Friedman, "A Methodology for the Discussion of Contour: Its Application to Schoenberg's Music," Journal of Music Theory 29/2 (1985): 223-48; Elizabeth West Marvin and Paul A. Laprade, "Relating Musical Contours: Extensions of a Theory for Contour," Journal of Music Theory 31/2 (1987): 225-67.
21See Wayne Slawson, "The Color of Sound: A Theoretical Study in Musical Timbre," Music Theory Spectrum 3 (1981): 132-41.


