Our explanations of music over the centuries have not lacked for their perplexities, their mysteries and even contradictions. One of the most persistent anomalies of our history has managed to embody all three: the conceptual duplicity surrounding the dyad of the fourth and the second inversion triad. In one breath both have been called eminently consonant, in the next breath dissonant. Unresolved, the paradox persists as a thorn in the flesh of a rational theory of music. Perhaps of greatest concern for us should be its continuing invocation as circumstantial evidence in debates over musical ontology, so its resolution is a matter of consequence.

Equivocation about the fourth can be traced back to the thirteenth century. Its enunciation as a harmonic principle came later, perhaps first in 1412 by Prodocimus de Beldemandis,¹ who pronounced thirds and sixths consonances, the fourth a dissonance (yet a dissonance "less than other dissonances"). Tinctoris reflects the same conceptual confusion sixty-five years later in The Art of Counterpoint, when he first claims the fourth as a perfect concord, only nine pages later to ban it from most uses as "an intolerable discord."² Clearly, the interval posed conceptual discomforts for those who were trying to square their received ideas with what they found in musical practice.

For the six-four chord, recognition of this curious ambiguity seems to have been concurrent with the fourth's waning consonance. Hugo Riemann claimed that Jean de Muris (1300-1351) rejected the six-four combination in his Ars discantus.³ Just over a century later, Franchino Gaffurio, in his Practica musicae,⁴ carefully (and I think speciously⁵) explains why the fourth forms a consonance between high-pitched voices of a texture but not between two of lower pitch. Explicit recognition, as a harmonic unit such as the six-four configuration, nonetheless awaited the time when harmonic theory would be defined by tertial chords. The same double standard, on behalf of both interval and chord, has been passed on to us as a Theory vs. Practice conundrum through the style-based harmonic traditions of the past three centuries.

Common-sense rules of classification demand that like things be classified under single rubrics. So it seems eccentric, at best, that a collection of identical pitch relationships be construed as diametrically opposed entities, at least in so far as a single property is concerned.⁶ One refuge from this common sense perspective has often been sought in the encompassing security blanket of Functional Harmony. As a formal concept it dates back to the awakened concern for rules of counterpoint expressed by such theorists as Tinctoris and Zarlino. But it comes to us most directly through Hugo Riemann, whose elaborate theory of parallel Klge is probably the most detailed extant exposition of the identity-follows-function harmonic concept.⁷ All kinds of harmonic mysteries have been nominally "solved" by the invocation of Functional Harmony's embracing principle, whose simplest statement would have to be "It is what it does."

Even if prone to over-zealous exploitation, the guidelines of Functionalism have nonetheless provided music theorists a healthy deflection from the temptation to explain all musical bits and pieces as isolated entities. In the Functionalist scheme of things a chord's identity depends largely on the company it keeps. And thus—or so the argument goes—the fourth (and the six-four) is sometimes consonant, at other times dissonant. Zarlino suggests this contextual rule-of-thumb when he allows that, although some intervals are inherently disagreeable in sound by themselves,

. . .when they are properly placed according to the precepts [which Zarlino is about to provide], the ear not only endures them but derives great pleasure and delight from them.⁸

Implicit in what Zarlino says here is a clue to an answer for this age-old question of the fourth: He clearly isn't talking about a one-dimensional raw state of sonance, the kind of isolated unions Pseudo-Aristotle had in mind when he asked, "Why is neither a double fifth nor a double fourth a consonance whereas a double octave is?"⁹ Zarlino is distinguishing between two levels of structure, sounds by themselves and sounds as participants within contexts.¹⁰ His distinction has been widely accepted yet insufficiently invoked. It is our misfortune that we continue, despite provoking urgings otherwise, to lump both levels of structure under the singular attribute of sonance.

An outspoken champion of the same distinction in our own time, theorist Norman Cazden, took great care to enunciate distinctions between appraisals of isolated sonorities from those transformed in some way by context.¹¹ But he too persisted in using the term dissonance as if it appropriately represented the two different data. "The 'chord of nature' itself, the C major triad," he once observed, "is a dissonance in the key of F." He reasoned that the chord's need of resolution to the tonic chord, its contextually imposed tension, made it "dissonant."¹² The benign acceptance of this marvelous aural alchemy, consonance transformed into dissonance, is so much a part of today's conventional wisdom that no heads turn at its utterance.¹³

The abolishment of this lexical aberration is overdue. A helpful step in that direction was made during the past decade with a growing recognition that concept-categories, rather than what we hear, sometimes underlie our problems of classification. In the case of the fourth and the six-four chord I'll argue that an unfortunate linguistic shift lulled us into using a single qualitative term (sonance and its derivatives) when referring to incompatible phenomenal conditions. Mere divisions of the sonance camp, like Norman Cazden's use of "systemic dissonance" as opposed to "acoustical dissonance," are at best cruelly misleading. And finally, I'll attempt to explain the perceptual conditions that have fed the paradox in the process.

We aren't talking about a rare problem. This is an error of one cloth with a number of others that cripple conceptualizing about music, and it has impressive relatives in the broader intellectual world. It's the kind of error Gilbert Ryle liked to call a "category-mistake," the sort that "represents the facts of mental life as if they belonged to one logical type or categorywhen they actually belong to another."¹⁴ In the case of the fourth and the six-four chord, we can isolate perceptual conditions clearly dominated by emergent properties that are the protagonists in this confusion of categories.

I use this term emergent in the sense it is used by Gerald Edelman, as a product of linkages of groups of neural signals within regional mappings in forming "new associative functions," in establishing more global mappings,¹⁵ properties of different perceptual chunkings. An emergent property is the unique product of a combination of properties, something unprovoked by the one property alone. But I have no wish to speak merely of words; my focus, ultimately, will be on the dynamics within and the causes for this one small piece of the tonal experience.

 

The Case of the Fourth

James Tenney tells us that the words consonance and dissonance have endured at least five different meanings since they were first cast in Pythagorean terms.¹⁶ Most critical for us here is the separation he unravels between what he designates as two Consonance-Dissonance Concepts, which I'll abbreviate to CDC-2 and CDC-3. His distinctions help us to better understand how we often use the qualifiers of sonance as if we were describing identical aural states, when in fact we are not.

CDC-2 encompasses the sonorous effect of simultaneous pitches, whose parts fuse or blend perceptually in relative degrees of unity, the condition Leonard B. Meyer has urged us to reserve for the terms concord or discord (see note #10). This phenomenal meaning for sonance can be traced to the very beginning of Western polyphonic music; it flourishes today, especially from the boost Carl Stumpf gave it in the late nineteenth century in his notion of Tonverschmelzung. It is the basic condition William Holder described so vividly in the late seventeenth century when he spoke of the dis-sonance of a minor second played on low organ pipes—perhaps an extreme case of the condition—as

such a Battel in the air between their disproportioned Motions such a Clatter and Thumping, that it will be like the beating of a Drum, while a Jigg is played to it by the other hand. ¹⁷

By contrast, CDC-3 began to emerge along with interest in the interweavings of counterpoint during the early fourteenth century, a product of attention focused on the way intervals "behave" and how chords "sound" within different contexts. This is an old story for musicians who know something of the history of structural conceptualizations.

The very differences of these two representations, Tenney's CDC-2 and CDC-3, cast a revealing spotlight on the fourth as interval. In the eleventh century, Guido d'Arezzo pronounced (in the Micrologos) that two tones forming a fourth create a smooth, congenial union when sounded together. So, added to the ambivalence of fifteenth-century theorists such as Beldemandis and Tinctoris, Zarlino's contradictory claim of five centuries later, even with his proviso of a determining context, must give us pause. And waters are muddied even more during the years between Guido and Zarlino when several theorists (such as Hieronymus Cardanus in 1574) ranked the fourth in a median category, between "true consonance" and "true dissonance." Those theorists so-ruled because, although judged dissonant in itself, they too found the interval consonant in combination with certain other intervals. Indeed, there is a veritable seesawing of conceptions of the fourth from the time when Aristoxenus lauded it as "the first of consonances."

I think Professor Tenney has hit on a principal source of the paradox that has dogged the fourth. More than any other writer, he has most clearly bared the shift away from isolated interval to the multi-dimensional condition of interval-within-context, something known all along yet rarely dealt with beyond the anecdotal.¹⁸ Sloppy shifts in defining language aren't rare. But they lead to troubling confusions when they occur without alterations or replacements or augmentations of the single descriptive rubric, like sonance, to fit phenomenally different instances.

Having recognized the lexical impropriety, Tenney encounters hard times in attempting to define perceptual causes for the interval's ambivalent status. In the long haul, those causes are critical. He acknowledges two possible sources. The first he timorously introduces as "a kind of incipient perception of harmonic roots." But this explanation arouses no taxonomic resonance in him. As he mentions, the conceptual undergirding that could underwrite it was developed much later than recognition of the condition. So he defers to that cunning old maxim " No concept, No percept," nonetheless recognizing in harmonic roots a possible cause worthy of "further consideration." Then he turns to a second speculated cause, one more to his liking.

This second, his preferred cause, is as disingenuous as it is fragile. It derives from the way spectral pitches produced by some intervals, one of them being the fourth, might form dissonances that would interfere with the communication of phonemes in a text. As Tenney explains it, such cloudings could pose an impediment for music in which a doctrinal message is meant to be conveyed, certainly a grave consideration for sacred polyphony of the period in question. This interference could arise within the fourth from a chafing between the lower pitch's third partial and the upper pitch's second partial, as shown in Illustration No. 1.

 

Illustration No. 1:Spectral dissonance of the fourth

 

And as Tenney puts it,¹⁹

the fourth is the only one, among the consonances of CDC-2, in which some partial of the upper tone falls within a "critical band" of one or more of those first three partials of the lower tone . . .

This circumstance is particularly compelling in his judgment, for it gives the fourth a quality shared by "other dissonant intervals." And, pressing the point further, he claims that this spectral colliding interferes in such a way that textual intelligibility seems destined to suffer.

Given the usual tessitura of the lower voice in polyphonic music of the 14th through 16th centuries, these first three partials would lie within the same frequency-range as the first two vowel "formants," whose presence and accurate representation in the spectrum of any vowel sound are essential to the intelligibility of that vowel.²⁰

An impressive idea. But it strikes me as excessively complex and remote as an explanation for a relatively simple and direct perceptual event.

After all, the conditions that lead to our distinctions of consonant or dissonant are surface matters—at least they certainly are in the sense of CDC-2.²¹ And if this spectral "dissonance" sparked the fourth's onerous reputation, we must wonder how it could have been so acceptable to the author of the Scholia enchiriadis (ca. 900), when he described the diatesseron (fourth) of parallel organum as the interval that produces "a most admirable smoothness of harmony" if performed "with proper diligence."²² That same medieval author furthermore appears not to have noticed that a string of successive fourths might garble the vowels of Non qui vivimus, benedictus Domino ex hoc nunc et us que insaeculum, which is the text used in his illustration. And moving several centuries later, it seems reasonable to surmise from the evidence at hand that the fourth's alleged garbling of the holy message was not the sort of thing troubling the venerable Council of Trent, mid-sixteenth century.

Leonard B. Meyer resorts to a similar yet different explanation of the fourth's alleged "acoustical dissonance." He attributes it to the expanded distance, in Renaissance polyphony, between bass and an upper voice .²³

When the 4th [ - ] is expanded by one or two octaves . . . discord is stronger because it is produced by the clash between a fundamental and the fairly strong third partial (Ill. 5b).

 

Illusration 2: Meyer's Ex. 5b: Conflicting spectral components of the expanded fourth.

 

But this hypothesis is as frail as Tenney's. Regardless of whether the textural "space" of Renaissance polyphony did or did not expand, such an explanation rings hollow when its full consequences are examined. If true, sixths (even without expansion) would have suffered the same fate as fourths, and this doesn't square with the abundance of sixth-chords in late-medieval repertories, all conceptually sanctioned as consonant, even "sweet to the ear."

 

Illustation 3: Conflicting spectral content of expanded sixths

 

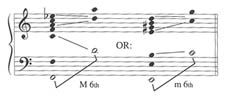
Let us presume—and only because it seems to be such a popular notion—that some sort of spectral interference, whether Tenney's or Meyer's or both, was in fact operational, corrupting the fourth's sonance and thereby subjecting it to stringent contrapuntal controls. Even so, we still must ask: Can one so casually drop the condition of interval roots as a potential cause for the fourth's sudden disrepute? Maybe the interval's innate "acoustical tension," dubious though that may be, was exacerbated by newly introduced syntactic pressures. Or, more likely, perhaps dissonance is only a handy but misleading substitute for a more accurate but less understood descriptive term, like unstable, dynamic (as opposed to static), mobile, or active. Why talk about dissonance in the first place?

We observed earlier that Tenney is reluctant to find the fourth's unfavorable status in anything related to interval roots or tonality. Meyer doesn't even mention them. Tenney justifies his reluctance, as we noted, by reminding us that the historical record doesn't support the roots/tonality explanation: Theoretical concepts embracing them were not yet developed.²⁴ And this is a crucial point. Indeed, it raises one of the truly alluring epistemic questions of twentieth-century musicology: Must we presume that, lacking a formalized concept, one must infer the absence of a related percept? It's a pertinent question, and its answer, although convoluted, is decisive to this part of our story.

 

The Thorny Issue of the Concept-Percept Chain

Granted, it's not easy to speak with conviction about the musical substance, as experienced, of times long past. I possess only circumstantial evidence of what a theorist of the thirteenth century experienced when he said: "That's dissonant, the other is consonant." And for this simple reason, musicology's most astute minds have warned repeatedly that we thoughtlessly impose our own culture-based biases on artifacts of earlier eras, even with the best of intentions.²⁵ Speculating about conditions left unexplained (or even unmentioned) by contemporaneous observers is at best risky, at worst fatuous. In this sense, even our West-European musical heritage is a foreign country, a body of artifacts whose remote ethnicity keeps us from understanding them as natives. Historians Leo Treitler²⁶ and, later, Frederick Bashour,²⁷ and theorist Carl Dahlhaus²⁸ are among the most prominent scholars who have insisted that theories fabricated after-the-fact, theories lacking the conceptual underpinnings of their times, play dubious (if not damaging) roles in descriptions of music. The larger issue, as it pertains to music, has been argued in depth and at great length from several perspectives, mainly epistemic and historical.²⁹ Speaking directly to the issue before us here, Thomas Christensen warns against irresponsible inferences of tonal traces in "pre-tonal musics." We risk "projecting our own culturally biased conceptions of tonality, however defined, upon a repertoire for which it has no conceptual basis."³⁰ And, strengthening his warning three pages later, Christensen adds that

any theorist risks obvious anachronism by interpreting the music only in the light of norms that were not consolidated until a later time. It is a kind of "geneticist" fallacy to pull out of context isolated features of a composition or theory text and posit them as tokens of tonality simply because they may empirically correspond to features that in later contexts are semiotically interpreted as clear tonal signs.

Professor Christiansen's concerns are unquestionably prudent. But his stance too readily replaces careful inference with the void of a rigid nominalism. Indeed, two aspects of what he seems to be saying are unacceptable as a ground for scientific inquiry: (1) that a conceptual basis is the conditio sine qua non of meaningful percepts, and the related conclusion (2) that "empirical correspondences" are readily nullified when the historical record carries no confirming verbal report. I tend to believe that something in a fourteenth-century virelai that sounds to my ears like something in a twentieth-century pop tune possesses a strong basis for conceptualized correspondence as well. I tend to believe that Sumer Is Icumen In projects a very clear tonic—a tonality—although I know those concepts were not a part of fourteenth-century discussions of pitch structure. Must I seriously and legitimately assume no cognitive-perceptual norms in common with my late medieval ancestors?

Music isn't alone in this discomfiting limitation. After all, the whole of history is filled with causal explanations that followed long on the heels of the persistent natural phenomena they explain. As starters, let us remember that there was no rational explanation of our blood's circulatory system until the twentieth century, no plausible explanation for the earth's gravitational field until the eighteenth. We remain convinced, nonetheless, that our fourteenth- and fifteenth-century forerunners were parties to both such phenomena. Even less tangible attributes also are at stake. As anthropologist Ellen Dissanayake³¹ reminds us,

. . . not having a word for something is not proof that the something does not exist: Many societies have no words for "love" or "kinship," yet these abstractions are evident to the outsider who names and then looks for them.

The fact is that our forebears lived with uncountable "natural phenomena" that stimulated unending speculative diagnoses, even though their precise natures and actual causes escaped detection. Some of those diagnoses merit only a good belly-laugh today. Persons of all intellectual levels in medieval France were convinced that the discomforts of gout were produced by leaking morbid humors. That painful state's relation to inefficient uric acid metabolism awaited modern chemistry for its discovery. Yet it seems reasonable to believe that the same metabolic imbalance was as much the cause of fourteenth-century inflamed joints as of those suffered during the twentieth. Should we nonetheless retain, for all persons prior to, say, 1800, their quaint contemporary explanation? Does historical concurrence grant a special kind of epistemic privilege?

 

The More Things Change, The More . . .

Is it improbable that what pre-Baroque listeners heard was subject to the influence of hierarchic pitch vectors—to the play of harmonic roots—long before their incorporation in such fancy explanatory frames as fundamental basses? Is it improbable that the fourth's potentially destabilizing root vector provides a better explanation for its mercurial sonance ratings than those tertiary partials of Tenney's and Meyer's? There is abundant evidence in pre-eighteenth century music that such forces were at play;³² there is circumstantial evidence in contemporaneous treatises that correlates with that artifactual evidence, and our own experiences offer a homely guide to an understanding of musical circumstances remote from our time and culture—assuming, that is, that the perceptual machinery of Homo sapiens sapiens has not endured major mutations over the centuries.

To deal with the latter first, whole populations have lived and died since Rameau's Enlightenment without the foggiest conceptual grasp of harmonic roots or interval inversion, of tonics or tonality. And yet, living, those many listeners effectively intercepted the tonal messages of nursery songs, patriotic and religious hymns, marches and pop tunes the folk furniture of daily musical fare that eminently displays those properties. Empirical studies of perceptual development show that a normal infant recognizes its mother's voice by the age of one week.³³ By the age of six or seven years it will have gained basic musical competence within auditory space.³⁴ Even before that ancient age, he or she can identify and respond appropriately to compositions that make up the daily listening repertoire, from Barney's theme to Dorough's "Multiplication Rock." Children achieve those competencies despite conceptual ignorance of the harmonic series (as a basis for timbre) or of their music's dependence upon a host of other imbedded properties, things properly "known" and talked about only by post-Renaissance "experts."

Or let us narrow our view. My own contemporaries—those who have bothered to know about such matters—rarely knew them before weathering with satisfaction a wealth of music, long before they had internalized, that is, its conceptual basis. So we know that conceptualization beyond the most primal kinds of associative "tendencies" necessarily follows perceptualization. To paraphrase Molière's M. Jourdain with some license, we are shocked to realize, one day, that for those many years we have been hearing lots of things without even knowing it.

And in this lies the clue to a revealing parallel. It suggests that the surge of explanatory prose coming along from theorists of the Middle Ages and Renaissance was of the same post facto caste. "Phylogeny recapitulates Ontogeny" becomes a respectable metaphoric reversal of the old axiom. In this sense, the dawning realization of harmonic inevitability that emerged, Gaffurio to Rameau, was to the history of music theory what my own personal realization of that condition was to me around the age of fifteen, when patches of "tonal objectification" emerged, long after the sensory-perceptual trappings were solidly in place.

For this reason, the historicist's "No-concept, No-percept" rule, abstractly arresting though it may be, must be accepted as wise suggestion rather than binding law. Even when preserved, prior explanations of musical phenomena, like those in the natural sciences, often prove to have been fragmentary, inconclusive, misleading, even pig-headedly wrong. If I approach sixteenth century music prejudicially, so did Zarlino. And if one must choose biases, I'll take mine over Zarlino's or Rameau's or Guido's. Granted the danger of dancing with phantoms, I enjoy an advantage: I'm blessed with a broader and richer musical base. I know, and thus have a basis for assessing, my predecessors' prejudices and blind spots. They knew nothing of mine. I possess more items to subsume in my more abstract musical "basic categories," as Jerry Fodor calls them.³⁵ With my contemporaries I possess the irreplaceable advantage of hindsight and psychic removal that no medieval nor renascent figure could muster. As biologist Peter Medawar once pointed out, renovated and replaced hypotheses can give the advantage of broader samplings and sharper insights. And thus they render obsolete, when they are well-formed, the theories they replace.

"Sometimes theories merely fade away . . . More often they are merely assimilated into wider theories in which they rank as special cases."³⁶

 

Emergent Properties of Time-Pitch Interaction

Indirect conceptual evidence that interval roots and the pitch focus of tonality were operational for listeners as early as the late Middle Ages, evidence a court of law calls "circumstantial," is found in two sources. The first is an emergent property, product of a new awareness of tones separated yet bound together over spans of time. This property is implicit in the temporal curbs imposed by theorists on particular intervals. The second is the incipient conceptual awareness of interval inversion within the octave. Both are manifestations of what Jamshed Bharucha has called the covariance, within particular contexts, of perceived conditions such as expectation, consonance, stability.³⁷ And as he adds, covariance being the rule, " . . .these terms refer to slightly different experiential aspects of the same underlying process."

Regarding the first kinds of evidence, temporal and harmonic properties were thought of, Middle Ages into the Renaissance, as separate yet tightly related components in a mutually affective bond. Theorists persistently expressed special concern for beginning and ending sonorities and for sonorities of extended duration. (Let us not forget that beginnings and endings define unique temporal events.) These concerns persisted with a renewed vigor into the Renaissance. Johannes Singer ruled in 1531 that "The bass should not be placed a fourth under the tenor for the duration of a breve or semibreve."³⁸ This cast the fourth into a highly controlled category, different from, yet side-by-side with, seconds, sevenths, and tritones. Then Cardanus's first rule of counterpoint, four decades later, held that dissonance (which for him included the fourth as an isolated interval) cannot occur "at the beginning or end of a piece, or on a long note, or on the first minim of a beat."³⁹

Most important for us in such rulings is the implicit recognition of duration as a contributing cause to pitch prominence and to its power to affect a pitch's contextual stability. They reveal and formalize as central the inseparability of temporal (including contextual, durational, and accentual) and harmonic properties. They make clear that learned musicians, long before the end of the sixteenth century, were fully conscious that intervallic inequality can be uniquely amplified by temporal conditions. Some intervals aren't allowed to occur in certain durations except in narrowly prescribed ways. If they sound for too long or if they are articulated in structurally prominent locations (whether as beginning or ending or as agogic or metric accent) harm may be done their surroundings. Nothing less than musical continuity itself is at stake; a newly acknowledged factor posed the threat of musical disturbance. And as Tenney concludes,⁴⁰

that disturbance could not have been caused by the same aspect of "sonorous quality" which had determined a dyad's dissonance status in the 13th century.

But what Tenney neglected to say is that its continued description under the sonance rubric was an elemental blunder. It is a quality removed from the kind of sympathetic resonance the fusion, the smoothness and togetherness emphasized in early discussions of consonance. If we pause just long enough to recall the sound of the isolated fourth (qua CDC-2), compared with seconds and sevenths, it's hard to deny Tenney's claim: The fourth's barren openness is not to be compared with more pregnant intervals, intervals Descartes would later claim "keep the ears busier."⁴¹ Something else had to be the cause of its banishment to transitive roles.

The evidence is imposing that the fourth's disturbing trait emerged solely from those newly recognized contextual dynamics, not from humanity's perfidious assessments of sonance. The interval was singled out by theorists because of a growing awareness and objectification of two conditions of different yet inseparable structural levels: (1) the local phenomenon of interval roots, and (2) pitch focus within the more global condition of tonality. Caught in the spotlight of metric accentuation, terminal location, or excessive duration (or all three), an interval needed a robust root, a property eminently enjoyed by both fifths and fourths. Below (as in the fifth) was acceptable. But above (as in the fourth) posed a problem for musicians whose ears were intent upon a texture's lowest voice, especially in sonorities containing the tonic pitch.

The half-century separating 1475 and 1525 unquestionably witnessed a rift in music's conceptual fabric. Motivated by a flowering empiricism that would further loosen any remaining ties to the Boethian/Platonic/Pythagorean biases, theorists felt a renewed surge of interest in "how things sound" and a will to explain them that way. Within this period, as Benito Rivera has thoroughly documented, intervallic inversion became a conceptual given for a number of writers. Both Guillermus de Podio (Ars musicorum, 1495) and Franchino Gaffurio (Practica musicae, 1496) explicitly described the condition realized when a third, for example, is the remaining "image" of a sixth within the octave. That this realization was the fruition of something heard, rather than something deduced from notes or numbers, rings clear when Gaffurio remarks⁴² that

within the ambit of the octave a third is easily generated by the motion of a sixth, and a sixth is connoted by the presence of a third. Hence, by the fact that they are both imperfect, they seem to possess the same nature and property.

This notion of complementation within the octave was not a well-kept secret. It was echoed "almost verbatim," Rivera tells us, by Johannes Cochleus (in 1507), by Ottomarus Luscinius (in 1536), and by Luigi Dentice (in 1553). As Rivera furthermore explains, we can trust that theory was very much following practice in these revelations, that these properties made newly explicit—these "interpretations"—were lagging behind what had long been audibly apparent.⁴³ Even after 1550, many accounts written by astute observers still skirted direct statements about harmonic roots or inversion.⁴⁴

So harmonic inversion as perceptual datum certainly didn't have to await Zarlino's exposition in the Dimostrationi, much less Rameau's Traité.⁴⁵ And when at long last conceptualized, the mix was complicated enormously, at least by the early fifteenth century, by a dawning awareness of a more global pitch factor: the hierarchical kinetics of tonality. This development, with its embodiment as pitch focus in the triad, has been disclosed in depth by Don Randel.⁴⁶

 

The Fourth's Uniqueness

But we still are left with a nagging question. If intervals were known as invertible before the end of the fifteenth century, why did theorists treat the fourth as a functional dissonance, thereby denying it equal rank with its known inverse, the fifth? Does it not, as Gaffurio claimed for imperfect consonances, "possess the same nature and property?" The tightness of the temporal-harmonic bond persists during that time as a paramount issue of counterpoint, although the rule demanding perfect consonances at beginnings and endings begins to be relaxed around the end of the fifteenth century.⁴⁷ Gaffurio ruled that for beginnings the old mandate is now "optional rather than absolute," that imperfect consonances (meaning thirds and sixths) can occupy beginnings.⁴⁸ But the fourth never shares in this reform, not even later when the rule is further liberalized to include thirds at endings.

Clearly, the demand for a perfect consonance at beginnings and endings was axial: It ensured an enclosing clarity. It helped to project the pitch-class intended as central to pitch structure. (And it matters little whether one calls that condition centricity, tonality, modality, tonal coherence, scale basis, or pitch hierarchy.) The intervals eminently suited for that purpose were unison, octave, and fifth. Why not the fourth? Only one reason seems plausible: Heard as an extended duration, it projects an unequivocal root, but that root isn't its bottom. The fourth is an upside-down interval. In a prominent musical location it can project a troublesome configuration, especially as a final sonority. Topsy-the-Clown just isn't supposed to end the act standing on his head.⁴⁹

It is not inconsequential that the root potential projected by the fourth (I prefer to call it vectorial thrust) is as powerful as the fifth's.⁵⁰ And as with the fifth, when its duration is prolonged (and especially beginning with a metric accent) a prevailing tonal status quo can be disrupted (if not confirmed). Simultaneous fifths are about as scarce as fourths in two-voice textures after the fourteenth century; by that time even music of the Christian liturgy had veered toward a standard of tertial sonorities. It may be true that thirds and sixths are as "beautiful" and as "sweet" as claimed through the ages, but they are less endowed in one way unmentioned by medieval and Renaissance writers: They are less potent than fourths, fifths, and octaves in staking out their enveloping claims on a pitch hierarchy. For this reason they pose a lesser potential endangerment to the integrity of a texture's established pitch hierarchy.

The fifth does occur. But like the fourth, its use was restricted. It occurs most often, in some repertories exclusively, as a boundary sonority. Its barren transparency and bottom-heavy stability could provide the punctuative clarity appropriate to terminal points in the flow of a high-consonance texture, whether at finals or at ends of interior phrases. And thus it is that the equally consonant but "upside-down" fourth cuts a figure that "makes it unique among all intervals."⁵¹ Listeners prior to the sixteenth century were as immersed in and as perceptually persuaded by the shape of the harmonic series as we are (just as they were bothered by systemic excesses of uric acid). The series was their ready-made, if unconscious, associative template for pitch collections, as it remains for us today. The sounds of their world conveyed the same uni-directional gestalt, the same bottom-heavy spectral configuration. For this reason, postulating that the fourth projected a top-loaded root for a medieval listener is a less radical speculation than postulating that it did not.

And there is a simple overarching moral to this shaggy-dog tale: Matters of con-textual kinetics (qua "functioning" sonority) must be separated from those of harmonic sonance (isolated sonority).⁵² For this reason Paul Hindemith's intervallic "simplicity" and "power,"⁵³ Ernst Terhardt's root "clarity" and "saliency,"⁵⁴ and my own root vectors,⁵⁵ refer to conditions that are in essence different from the coinciding partials of Hermann Helmholtz,⁵⁶ the "fusions" of Carl Stumpf,⁵⁷ or the "Clatter and Thumping" described by William Holder. And since they are perceptually different, they must be called by different names.

The necessity for categorical separation, isolated sonority differentiated from sonority-in-context, was recognized but not sufficiently understood by pre-Renaissance theorists. It was not rigorously enforced, even after it became a critical (if yet unexplicated) part of the pitch equation after the tonality/key condition was conceptualized. Demand for the separation has been echoed repeatedly in our own century, even when the term sonance is retained as a cover for both. The "dissonant fourth" designation persists, as if it were bird of a feather with seconds, sevenths, and tritones. As early as 1905, Theodore Lipps, in his classic critique of Stumpf's notion of fusion makes the distinction paramount:⁵⁸

. . . when I declare the consonance of two tones pleasant, I obviously mean this particular consonance, the consonant relationship of these two tones. I don't think of tones within a larger context. In a context they are automatically no longer just these two tones but elements of a context. The question isn't limited to: What is the consonance of these two tones? Instead, it also is: In what relationships of consonance and dissonance do we find these tones within the given context? Or, What is the fabric of consonance and dissonance these tones are woven into, and how are they enmeshed within it?

That question isn't always so easy to answer. Regardless of how simple the problem of consonance for two tones may be, the problem of consonance (or dissonance) between a tone and an elaborate construct of tones, such as a melody, isn't simple.

It's too bad that an astute psychologist of Lipps' musical sophistication, or a music theorist of Norman Cazden's psychological insight, didn't move one step further to provide a new term to fit the need of their wise warnings, relieving our overworked sonance of its excess descriptive baggage. But they did not. This kind of unexamined dependency on a traditional category has sidetracked many a quest for understanding among some of the most venerable figures of history. Even the great Copernicus, whose mathematical and astronomical genius are celebrated, couldn't overcome his taxonomic naiveté in other domains. In The Sleepwalkers⁵⁹ Koestler quips that

If Aristotle had stated that God created only birds, Canon Koppernigk would have described homo sapiens as a bird, without feathers and wings who hatches his eggs before laying them.

And as we'll observe at the end of this discussion, indifference of musicians toward indefensible "category-mistakes,"as Ryle called them, has left us with a string of judgmental non sequiturs about the very substance of the art.

 

The Knottier Problem of the Six-Four Chord

Having acknowledged these issues of conceptual clarity, it seems nonetheless easier to dispose of the fourth's wrongful portrayal than that of the six-four chord. The latter's greater harmonic definition, because of its additional consonant intervals, could be expected to neutralize its unfavorably disposed root. That top-loaded root may well bear on a chord's or interval's contextual flexibility, as we have argued, but it seems an unlikely agent for altering sonance all the way from the con- to the dis- side of the fence. Even early writers (Gaffurio, for instance) found the first inversion triad suitably consonant except at phrase endings. And further, we know that patches of sixth-chord style, in late medieval English music and in the fauxbourdon of fifteenth-century Burgundian music, elevated successions of that sonority to the rank of a harmonic convention. So root position alone must not be demanded for contextual respectability. Which leads to the gnawing suspicion that other factors must have fed the age-old truism of the six-four chord's "dissonance." Maybe sonance isn't involved at all.

 

Emergent 'Dissonance' and 'Premature Chords'

To my knowledge, a commanding agent of the six-four chord's tarnished reputation (aside from its stake in the fourth's status) has been overlooked. This neglected factor is especially fascinating because it introduces an emergent property in a more direct way, something we know occurs in the marvels of the musical experience yet which we rarely talk about.

The basis for this governing emergent property, as it pertains to the "dissonance" of the six-four chord, is temporal. Its full constituency is rhythmic and harmonic, the shaping of the one rubbing off on the other. It involves a rigid phrase template that has virtually defined the style-role of the six-four chord through some four centuries of music. This is not to say that the six-four chord doesn't appear in other guises. But those other versions (the "Passing Six-Four," the "Pedal Six-Four," etc.) have played less formidable roles in the textures of traditional music. They seem to have been discussed in the theoretical and pedagogical literatures only for contingent reasons: After all, if the chord is claimed to be dissonant, then compensatory "rules" covering all of its occurrences must be formulated.

The origins of this particular emergent "dissonance" can be traced back to cadences of Renaissance polyphony,⁶⁰ music in which the dominant-to-tonic cadential pattern or at least its metric-intervallic-melodic ancestors had already been established as a stylistic norm. Illustration No. 4 shows the end of a Lauda by a composer who bridged the fifteenth and sixteenth centuries. It embodies the rhythmic, contoural, and some of the intervallic properties involved in the later archetype.

 

Illustration No. 4: Giacomo Fogliano (1473-1548), Lauda, final measures

 

Observe three points here: (1) the final tonic is anticipated melodically with the syncope of the second measure; (2) this F-tonic forms a momentary 4 - 3 suspension with the bass on the last half of the measure; and (3) a terminating succession of V - I seems imminent (even though a deceptive cadence to vi actually follows here).

Much the same melodic, rhythmic, and harmonic conditions prevail in Illustration No. 5, the final cadence of an anthem from a century later. But an explicit second inversion tonic chord inhabits the second beat of the next to last measure,⁶¹ a passing chord to the 4 - 3 suspension that comes on the next beat.⁶² Note also that the anticipation of final tonic remains as a melodic template.

 

Illustration No. 5: Orlando Gibbons (1583-1625), Anthem, "O Lord increase my faith" (ending)

 

With negligible deviations, this basic compound of rhythm/melody/chords prevails in the repertory of Western art music, fifteenth through the nineteenth century, and especially during the period of Common Practice. It is the ancestral paradigm of the I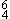 - V - I cadence of 1700-1900. The same basic figure, bearing a 4 - 3 "resolution" cliché within a larger cadence pattern, would have been plentiful in earlier music except for one thing: the prevailing vicissitudes of counterpoint. The cadential norm for late medieval two-part textures was the kind of 6 - 8 pattern shown in Illustration 6a, its steps in contrary motion controlling the voice leading.

 

Illustration 6a, b, c: Voice leading in the archetypal 2-voice cadence

 

If the "more harmonic" V - I pattern of later polyphony had prevailed, opportunities for the 4 - 3 succession, as in Illustration 6b, would have been possible. But it was not a part of the stylistic climate. By the time the V - I fundamental bass had entered musical currency it had accumulated another voice, one that usually formed an unequivocal dissonance, of the kind shown in Illustration 6c.

Illustration 7 shows a typical instance of the later, more robust realization from Beethoven, the tonic chord coinciding with metric accent.

 

Illustration No. 7: Beethoven, Piano Sonata, Op. 2 No. 1, Minuetto

 

The Haydnesque realization of the same terminating convention differs only in negligible details, as in Illustration 8.

 

Illustration No. 8: Haydn, Symphony 88, II (Andante), mm 1-8

 

 

Rhythm is most important for us, in this passage as in the Beethoven: It is dominated by the sing-song (4 [2 + 2] + 4 [2 + 2 ]) phrase structure established from the beginning. Even the Haydn, despite its play of melodic syncopes, projects the same duplex template. Notice further how both melodies resurrect the anticipation of final tonic that was conventional in music from two centuries before,⁶³ and that the last two examples unequivocally bear the I - V7 - I chord pattern, their six-fours falling on metric and agogic accents.

Let us recall that the six-four chord, like dyads of the 4th, has endured a contentious history. One distinguished analytical tradition has even held that, pitch content to the contrary, it's not actually a tonic chord. Indeed, the argument goes, mere appearance is deceptive; one must recognize the chord's function as an incipient dominant chord, within the cadential gesture, to understand its true nature.⁶⁴ But this argument derives from a skewed application of the functional perspective. Its designation of the six-four chord as a dissonance-to-be-resolved is analytically inconsistent as well as lexically confusing, mainly because it is incompatible with so many other aspects of conventional harmonic theory. If we apply the rules of tertial harmony with dogged simplicity, then 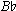D and F sounding together as a rhythmic unity constitute "a 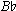major chord." And furthermore, if F is at that chord's bottom, it necessarily follows that the structure is "a second inversion triad." Simple enough, by the surface rules of chord nomenclature. And we must keep in mind that we are talking about a harmonic event that falls on a metric accent and whose duration is usually equal at least to the meter's basic duration (or "beat value").

This manifest kind of reasoning has at times been shunted aside by the invocation of raw perception, a show-down kind of test. Those who argue an unexamined brand of Functional Harmony make a simple request of unbelievers: "Listen to it in context." And the usual forthright response to such unwashed empiricism is predictable: The chord at beat one in Haydn's seventh measure falls short of the release of harmonic tension, the resolution expected from a true consonance. Backed to the wall, most people agree: It's unstable; it demands continuation to a chord of greater resolution; it just doesn't really seem final. It is dissonant. And likewise the triad in beats 1 and 2 of m. 11 of the Beethoven.

 

The Curious Case of the Non-Paradox

So the acid test, informal and anecdotal though it be, has helped to perpetuate the six-four chord's shady reputation. Under these circumstances it's a certified dissonance. But let us beware: These imposing jargons merely switch the rules of our categories: Now we are occupied with expectations of WHERE the chord may be headed, as part of a rhythmic thrust, rather than with WHAT are its inherent sonic characteristics. And thus it is that all of those venerable figures of the past who have applied the term dissonance to such formations could and should have been more accurate in their descriptions.⁶⁵ Harmonic oranges are inadvertently mixed with temporal apples. The instability, the inconclusiveness of the six-four chord in such instances—its dissonance, if one must—is not a condition of sonance (if by that term we refer to the inherent quality of comparative fusion/blend/merging of a pitch coalition/alliance/amalgamation/integration, etc. that one interval possesses vis-à-vis another interval). On the contrary, the chord's condition is provoked by a bundle of as yet unfulfilled rhythmic expectations. Temporal equivocation prevails, not harmonic dissonance.

As I remarked earlier, both Haydn's and Beethoven's passages set up compelling phrase templates. By their fourth measures the listener is caught on the tracks of a periodic 3-beat X 4-measure pattern, a time-grid whose propulsion ends only with the arrival of its final unit. Typically, the underlying chords and bass line are co-conspirators in driving home this simple periodicity. Observe the high linear and harmonic directionality in the Haydn, as represented in Illustration 9.⁶⁶

 

Illustration No. 9: Bass line and harmonic progression of the Haydn Symphony 88, II

 

So Beethoven's third phrase cannot conclude, at least not with any sense of rhythmic propriety, anywhere except in measure twelve, Haydn's in measure eight. The tracks laid down by the preceding patterns (bass line contours, harmonic rhythms, and phrase rhythms) preordain just these destinations. And thus the respective harmonic (I chord) and melodic (tonic pitch) projectors of cadence in measures eleven (Beethoven) and seven (Haydn) are swept past by the overpowering thrusts of other properties, carrying us forward. As potentially terminating events, which is their lot "in the style," they are rendered unexpected⁶⁷ by phrase-rhythm. In the same way auditors perceive as "more dissonant" a target chord that is unexpected, the six-four is denied the high degree of tonal stability its intervallic content could convey in more propitious surroundings.

Couched in more general, more cognitive terms, the six-four chord, like the fourth in polyphony, is welcome only within tightly controlled instances; it can stick out like a sore thumb in some of the rhythmic/harmonic schema that emerge in most musical styles of the past. The listener's dominating expectation, upon hearing the formulaic six-four cadential chord, is one of continuation: Stability will be reached only with a subsequent metric moment.

The paradox was in fact all along only a chimera. The conditions required for paradox, the presence of self-contradictory "truths," were never present; people were hearing a temporal thing and reporting it by another name. It is curious that this phenomenon, rhythmically-imposed instability as sonance, has remained so clouded for so long. It is yet another instance of a style-bound condition being falsely interpreted as confirmation of a music-universal, in this case the dissonance of fourths and six-four chords. Can we wonder that both retained their paradoxical reputations on into the twentieth century?

I'm not aware of any other theorist's discussion of this fascinating emergent condition, this rhythmic offender responsible for centuries of misunderstanding of (and false attributions to) the second inversion chord. Thom Clifton came close to recognizing and enunciating its basic content of rhythmic/harmonic ambiguity. Ruminating about the difference between acoustical and experiential interpretations of sonance, he observed⁶⁸ that

. . .the displaces the not only in time but also in space. The presentation of the is heard as a projection of tones from the harmonic environment of the dominant function. This projection, or outward-bound motion, in presenting a certain instability, is counteracted by the pull of the harmonic environment itself. The result is the tension we call dissonance.

He calls attention here to a rhythmic/harmonic non-conformity. What he describes is the listener's expectation of V (), the style-induced probability of the dominant. What he seems to have overlooked is the more primitively-driven expectation: a later ending for the phrase, an outcome dictated by the short-term memory of previous phrase lengths.

The dissonance charge, even as it was perpetuated by Clifton, turns out to have been a bum rap, a case of guilt by association. In part, the six-four chord was a victim of its own stellar role in the repertory that formed the exemplar base of modern music theory, as The Cadential Six-four.

A more appropriate description of the perceptual effect is Premature Tonic. It is the chord's archetypal location in a projected rhythmic flow that denies it the closure conveyed by concurrent melodic and chordal content.⁶⁹ And this has been a principal colluding source behind the chord's apparent paradoxical status. It should have been obvious all along that its sonance, as a collection of intervals, is not that different from its root position and first inversion cousins. Calling it dissonant commits a conceptual injustice as well as an oversimplification of a complex moment in musical time.

Curiously, the warnings made by Theodore Lipps were heeded by some of the authors of theory texts early in this century. Ferdinand Louis and Ludwig Thiulle seem almost to echo their German colleague in their Harmonielehre of 1907 in assessing the sound of the cadential six-four. Unspecified extenuating circumstances come to bear:

These formations, considered in isolation, are thoroughly consonant. But the context in which they appear forces on our ear a conception in which they actually seem dissonant .⁷⁰

It's a pity that theorists have been willing in the subsequent ninety years to accept this state as a given, without questioning the propriety of the vocabulary, without seeking an explanation for the curious conditions that might make consonance seem to metamorphose into dissonance.

 

Broader Historical Implications

The significance of what we have discussed extends well beyond the prosaic subject of dyads of the fourth and of six-four chords. As I mentioned earlier, the issue of proper pedigrees for both is not among the hot issues of current musicology. But beyond these peccadilloes, imprecise bookkeeping of perceptions can lead us dangerously astray conceptually, particularly when one specious "fact" is enlisted to confirm another. For this reason alone, our recognition of the "dissonance" of fourths and six-fours as the product of emergent conditions has a more profound importance in two ways.

First, we are reminded yet again how risky it is to approach explanations of music as if it persists as the singular dimension of pitch. The danger lies in drawing false conclusions, even about the presumed single property itself, in addition to losing sight of the broader ultimate goal, which is definition of the whole musical event. Musical properties are easy to isolate, but their natures are hard to know except as they interact and co-depend within the musical flow. In this sense, a carefully monitored functionalist perspective is an essential part of the epistemic toolbox. But its informative value plunges when its products are confusedly applied to things in themselves as if they were independent of their surroundings.

Second, and more importantly, unraveling this time-worn paradox has one particularly profound result: It helps to dispel a rumor that has informed one wing of music analytics over the past half-century. Holding that the harmonic series bears no relevance to the musical experience (beyond its obvious relationship to timbre), the rumor took hold in the wake of the fashionable canon of abstract rationalism that flooded music theory after World War II, when Serialism became academically fashionable. It reduces the listener to a Cartesian tabula rasa, the structural wherewithal of music to a set of locally imposed commandments, rules neither rooted in nor bounded by preferences nor inclinations peculiar to the listener. Like the game of checkers, the musical experience is imagined as progressing by moves founded solely in arbitrary, if ingenuous and internally consistent, restrictions.⁷¹ The notion that some primitive urges to structuring, whether genetic or epigenetic, beckon the musical impulse along its way is tolerated only as a curio from a throwaway past.

This infatuation with perceptual relativism gains some of its credibility by default: The rumor feeds itself in claiming that centuries of fallacious attempts to show a causal role for the harmonic series in music-structural matters is ample proof that the idea itself is untenable. After all, the history of the discipline of music theory is studded with all sorts of fanciful fictions, from "phonic overtones" to Unterklänge, and the fourth and six-four chord provide confirming case histories. In the ninth century the fourth is a consonance; by the seventeenth century it is a confirmed dissonance. The solitary six-four chord is consonant; but running with the wrong crowd it becomes dissonant. No great leap of faith is required, from these pairs of contrary premises, to the conclusion that the very distinctions, consonant/dissonant, have no real meaning beyond an arbitrarily defined context. Clearly, it seems to follow, they are no more than "linguistic rules"⁷² passed on to us from a less enlightened past.

Champions of this persuasion are convinced that there is no place for the harmonic series in explanations of pitch structure, no role in cognition as a musical paradigm.⁷³ And the checkered careers of the fourth and the six-four chord make a credible Exhibit A for the prosecution. After all, the fourth is a confirmed dissonance, even though it occurs lower in the harmonic series than thirds and sixths. So we are reminded, ergo, that "the succession of intervals in the overtone series does not correspond to the categorizations of 'consonant' and 'dissonant', even in relative terms."⁷⁴

Even astute theorists of a less nominalist persuasion retreat when faced with what appears to be the unimpeachable dissonance of the fourth. For instance, Fred Lerdahl and Ray Jackendoff add to this untruth an irrelevancy, thereby producing a deductive deadend:

Since the fourth (generated by the overtone series) is dissonant and the minor triad (not generated by the overtone series) is consonant, derivation from the overtone series is [not] a sufficient condition for consonance, even in the musical idiom most familiar to us.⁷⁵

But now we know that this faultless logic is applied to erroneous premises, that our imprudent taxonomies have led to a conceptual delusion. The emblematic argument is punctured. And that being true, all collateral cases on the docket should be similarly dismissed.

---

¹Hugo Riemann, Geschichte der Musiktheorie (Leipzig: Hesse, 1920), 267. The Tenney and Rivera sources referred to subsequently are rich in historical background on this matter. Glen Haydon's The Evolution of the Six-Four Chord (Berkeley: University of California Press, 1933), remains the unsurpassed source regarding the six-four chord's occurrence in the repertory, 13th to mid-17th century.

²James Tenney, A History of 'Consonance' and 'Dissonance' (New York: Excelsior Press, 1988), 44-45. In the dedication of the same treatise Tinctoris pointedly contradicts a hallowed Pythagorean position passed on through Boethius, when he denies a Music of the Spheres. See Oliver Strunk, Source Readings in Music History (New York: W. W. Norton, 1950), 198-99.

³Riemann, Ibid., 263: "Hat der Diskant die obere Sixte, so erhält der Contratenor die untere Terz, Quint (die hier am besten klingt), Oktave oder Dezime, aber nicht die Sixte."

⁴Irwin Young, trans., The Practica Musicae of Franchinus Gaffurius (Madison: University of Wisconsin Press, 1969), 141.

⁵I say "speciously" because I agree with those who hold that a respectable theory of sonance will prove to be operable throughout the pitch range of music: the minor 2nd A - 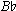is more dissonant than the major third A - 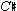, regardless of register.

⁶This doesn't mean that two chords of identical interval content (such as major and minor triads) are identical except in terms of sonance. The "shape" of a chord, i.e., the way its intervals stack up, is a critical determinant of sonority. For this reason, Wagner's Tristan chord will never be mistaken for a V7 from Rameau's Acante et Céphise, although it contains the same interval content. Herein lies the critical limitation of sonority descriptions based solely on interval content.

⁷See Matthew Shirlaw, The Theory of Harmony (DeKalb, IL: Dr. Birchard Coar [2nd ed.], 1955), 398; and William Mickelson, Hugo Riemann's Theory of Harmony and History of Music, Book III (Lincoln: University of Nebraska Press, 1977), 64-65.

⁸G. Zarlino, The Art of Counterpoint, Book III of Istitutioni harmoniche, trans. Guy A. Marco and Claude V. Palisca (New Haven: Yale University Press, 1968), 53.

⁹(Pseudo) Aristotle, Problems, Vol. I, trans. W. S. Hett (Cambridge: Harvard University Press, 1924), Problem XIX, 34.

¹⁰Leonard B. Meyer urges use of concord/discord for describing the blend-quotient of simultaneities, consonant/dissonant for the relative tensions invoked by syntactic matters ("Nature, Nurture, and Convention," Convention in Eighteenth- and Nineteenth-Century Music, eds. Wye J. Allanbrook, Janet M. Levy, and William P. Mahrt [Stuyvesant, NY: Pendragon Press, 1992], 480). This seems plausible, but only until one realizes that the history of terminological convention, with its ready interchangeability of these two pairs, would never sanction such an easy solution. The lexical entanglement is made evident in the following, from the most recent edition of Grove's:

DISSONANCE. A discord, or any sound which, in the context of the prevailing harmonic system, is unstable, and must therefore be resolved to a consonance.

¹¹See Cazden's "Musical Consonance and Dissonance: A Cultural Criterion," Journal of Aesthetics and Art Criticism 4 (1945-46): 3-11, "Sensory Theories of Musical Consonance," Journal of Aesthetics and Art Criticism 20 (1961-62): 301-319, and "The Definition of Consonance and Dissonance," International Review of Aesthetics and Sociology of Music 11 (1980), No. 2: 123-168.

¹²Cazden, "Musical Consonance and Dissonance: A Cultural Criterion," 5.

¹³Richard Crocker commented over thirty years ago that "The anomaly of the fourth is so deep-seated that according to latest reports the issue is still in doubt." (In "Discant, Counterpoint, and Harmony," Journal of the American Musicological Society 15 (1962): 6.

¹⁴Gilbert Ryle, The Concept of Mind (Chicago: The University of Chicago Press, 1949), 16. Ryle's discussion here is about the mythic mind/body separation, but he touches elsewhere on the same mistake made in other domains, in this book and in his later Dilemmas (Cambridge U. Press, 1956).

¹⁵In Neural Darwinism (New York: Basic Books, 1987), 60-64, as well as earlier discussions of the processing of re-entrant interactions (page 26). As we shall see, none of the contributing properties in our instances of "dissonance," melodic, harmonic, or rhythmic, conveys instability, or ambiguity or"dissonance"on its own. But the mix does. As a whole, this also can be understood as an event of ambiguity, since the combined properties project contradictory messages of closure and non-closure. See W. Thomson, "Functional Ambiguity in Musical Structures," Music Perception 1 (1983): 5-17.

¹⁶Tenney, Op. cit.

¹⁷William Holder, A Treatise of the Natural Grounds, and Principles of Harmony, 1694 (2nd ed. London, 1731), 34. I am indebted to Norman Cazden, in whose work I first came across mention of Holder's treatise.

¹⁸Hindemith struggled with the same problem in his vague differentiation of Series 1 from Series 2 in the Craft of Musical Composition, I. See William Thomson, "Hindemith's Contribution to Music Theory," Journal of Music Theory 9 (1965): 54-56.

¹⁹HCD, 9. This, of course, is merely a variant replay of Helmholtz's long-discounted explanation (On the Sensations of Tone, trans. A. J. Ellis [New York: Dover Books, 1954], 182-87) of common partials (or not) as determinants of sonance.

²⁰Ibid., 49.

²¹An extensive discussion of consonance/dissonance differentiation in the Stumpf sense of fusion is in Theodore Lipps's, Consonance and Dissonance in Music (San Marino, CA: Everett Books, 1995), 55-79.

²²Strunk, Source Readings in Music History, 129-31.

²³Leonard B. Meyer, "Nature, Nurture, and Convention," 482.

²⁴Ibid., 48.

²⁵The warning was raised first, I suspect, by pioneering ethnomusicologists, such as von Hornbostel, who properly feared loading ethnocentric concepts on to the musics of non-European cultures.

²⁶In "Music Analysis in an Historical Setting," College Music Symposium 6 (1966): 75-88. Treitler's main concern is with later writers such as Heinrich Bessler who find tonality—even a very "basic form" of it—in the music of pre-Baroque composers such as Dufay.

²⁷Frederick Bashour "Toward a More Rigorous Methodology for the Analysis of the Pre-Tonal Repertory," The College Music Symposium 19 (1979): 140-53. Bashour argues (especially 141-43) the determining role of normative tonal relationships, as they can be inferred today, expectations grounded in music experiences in the auditor's culture.

²⁸In Studies on the Origin of Harmonic Tonality, trans. Robert O. Gjerdingen (Princeton: Princeton University Press, 1990). A sample of Dahlhaus's inflexibility on similar issues is his refusal to recognize tonality in music that doesn't conform to his definition (which comes from Rameau via Riemann).

²⁹For instance, Naomi Cumming, "Musical Analysis and the Perceiver: A Perspective from Functionalist Philosophy," Current Musicology 54 (1993): 38-53; the thoughtful exchanges of Paul M. Churchland and Jerry A. Fodor, brilliantly reported in Mark Devellis' "Is There an Observation/Theory Distinction in Music?," Current Musicology 55 (1993): 56-87; and Peter Schubert's "Authentic Analysis," The Journal of Musicology 12 (1994): 3-18.

³⁰In his review of Carl Dahlhaus's Studies in the Origins of Harmonic Tonality and Joel Lester's Between Mode and Key, in Music Theory Spectrum 15 (1993): 94.

³¹What is Art For? (Seattle: University of Washington Press, 1988), 35.

³²For a discussion of evidence in the music of the past and non-Western repertories, see W. Thomson, Schoenberg's Error (Philadelphia: University of Pennsylvania Press, 1991), 100-113.

³³Robert D. Walk, "Perceptual Learning," in Handbook For Perception IX (New York: Academic Press, 1978), 264.

³⁴Lyle Davidson, "Songsinging by Young and Old: A Developmental Approach to Music," in Music Perceptions, eds. Rita Aiello and John A. Sloboda (New York: Oxford University Press, 1994), 111-23; Howard Gardner, The Arts and Human Development (New York: John Wiley & Sons, 1973); and J. Piaget, Genetic Epistemology (New York: W.W. Norton, 1970). In Piaget's sense this understanding would be figurative, not necessarily operational. The latter phase comes with formal training. In a way, humans are pikers. Robert D. Walk reports ("Perceptual Learning," 274) that the white-crowned sparrow memorizes a model song between two and seven weeks after hatching, and this during a time when he can't even sing. But, of course, he ends up knowing only one tune!

³⁵Jerry A. Fodor, The Modularity of Mind (Cambridge, MA: MIT Press, 1983), 96-97.

³⁶Peter Medawar, Pluto's Republic (New York: Oxford University Press, 1982), 90.

³⁷Jamshed J. Bharucha, "Tonality and Expectation" in Music Perceptions, 217.

³⁸Benito Rivera, "Harmonic Theory in Musical Treatises of the Late Fifteenth and Early Sixteenth Centuries," Music Theory Spectrum 1 (1979): 88. My italics.

³⁹Tenney, HCD, 46. In this context discussions of the fourth in contemporary eighteenth and sixteenth century counterpoint manuals are instructive. Kent Kennan's explanation (Counterpoint [New York: W. W. Norton, 1959]) is noteworthy in view of the argument I make here: "The perfect fourth is a special case. Although relatively consonant acoustically, it is classed as a dissonance in this style because of its incomplete and 'top heavy' quality. . ." The 16th c. text of H.K. Andrews (An Introduction to the Technique of Palestrina [London: Novello and Co. Ltd., 1967]) lumps fourths with augmented and diminished intervals, seconds and sevenths; they "and their compounds are dissonant against the bass."

⁴⁰Ibid., 48.

⁴¹Descartes says this about the fifth, comparing it with the octave. See the Compendium trans. Walter Robert (American Institute of Musicology, 1961), 24. He made a similar remark about thirds and sixths in a letter to Mersenne of October [?] 1629.

⁴²Rivera, "Harmonic Theory in Musical Treatises . . . ", 93.

⁴³Ibid., 95 (my italics).

⁴⁴Descartes, for example, refers to the 4th as "almost a shadow of the fifth and its constant companion." (Compendium, 25.)

⁴⁵Riemann (Geschichte, 372) attributes the "discovery" to Zarlino; Shirlaw disagrees (Theory of Harmony, 51), opting for Rameau.

⁴⁶D. M. Randel, "Emerging Triadic Tonality in the Fifteenth Century," Musical Quarterly 57 (1971): 73-86.

⁴⁷Tinctoris in 1477, Gaffurio in 1496.

⁴⁸Rivera, "Harmonic Theories in Musical Treatises," 82.

⁴⁹My "upsidedown" figure of speech is implicit in Descartes' Compendium when he explains (page 25) the fourth's limited usefulness: For if we were to use the fourth above the bass, the fifth would always accompany it [as its harmonic shadow] and the ear would easily realize that the fourth has been merely displaced from its proper position to a lower one.

⁵⁰Reiner Plomp's empirical studies convinced him that fourth and fifth share a unique kinship because auditors confuse them with one another more often than either is confused with the tritone (which is closer in magnitude to both). See especially his "Detectability Threshold for Combination Tones," Journal of the Acoustical Society of America 37 (1965): 1110-1123.

⁵¹Tenney, HCD, 48.

⁵²Obviously, this is not my discovery. As the preceding resumé makes amply clear, it has been recognized for centuries. I make the point explicit in order to move into a discussion of how rhythm can project its own stability/instability dynamics, which can be mistaken for conditions of sonance.

⁵³Paul Hindemith, The Craft of Musical Composition, trans. Arthur Mendl (New York: Associated Music Publishers, 1945), 68-74.

⁵⁴Especially see E. Terhardt, G. Stoll, and M. Seewann, "Algorithm for Extraction of Pitch and Pitch Salience From Complex Tonal Signals," Journal of the Acoustical Society of America 71 (1982): 679-88.

⁵⁵W. Thomson, Schoenberg's Error, 404-07, and "The Harmonic Root: A Fragile Marriage of Concept and Percept," Music Perception 10 (1993): 385-416.

⁵⁶ H. Helmholtz, Op. cit., 182: "Just as the coincidences of the two first upper partial tones led us to the natural consonances of the Octave and Fifth, the coincidences of higher upper partials would lead us to a further series of natural consonances." Helmholtz lists these, through the minor third, p. 183.

⁵⁷C. Stumpf, Tonpsychologie II (Leipzig: Herzel, 1898), 37: "It is readily acknowledged that the octave sounds effectively like a unison, even when we can clearly distinguish two tones in it. Although this is nothing less than self-evident, it is still a most remarkable fact. The same property operates in a lesser way with fifths and fourths, even less with thirds and sixths."
Das die oktave dem wirklichen Unisono ähnlich klingt, auch wenn wir deutlich zwei Töne darin unterschieden können, ist allezeit anerkannt worden, obschon es nichts weniger als selbstverständlich, sondern eine höchst merkwürdige Thatsache is. Dieselbe Eigenschaft kehrt aber in angeschwächter Weise auch be Quinten und Quarten, ja bei Terzen und Sexten weider.
Compare Stumpf's reckoning with Johannes de Garlandia's (13th century), which Tenney quotes (HCD, 27): "A perfect concord is when two sounds are joined at the same time so that the ears cannot distinguish one voice from the other . . . "

⁵⁸Lipps, Ibid., 77.

⁵⁹(New York: Scribner and Sons, 1959), 212.

⁶⁰The historical significance of the six-four configuration is hard to overstate. It is forcefully argued in Glen Haydon's The Evolution of the Six-Four Chord (Berkeley: University of California Press, 1933). He traces it back to the thirteenth century (which has no particular bearing on our discussion), regarding it (p. 132) as an important part of the unfolding stylistic fabric of West European music. Its evolution shows a "formula" so important, in his judgment, that "it asserts a directive influence on the progress of the art."

⁶¹Some readers will prefer not to call this a chord of any kind. But if one does so designate it, its most appropriate functional name would be I .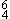

⁶²Cadential matrices in both the Fogliano and the Gibbons satisfy only four of Meyer's six requirements for a full-fledged six-four chord. Whether they were "heard" as six-fours in their day is beside our point; only rhythmic and intervallic mix concerns us, as a forerunner of the later convention.

⁶³I make no claim to an exhaustive search of earlier musics. For a thorough history, see Haydon's classic study. A common option contains a 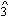- - 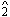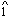descent rather than the tonic anticipation I focus on here. For additional discussion of the 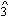- - 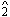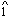see David Beach, "The Cadential Six-Four as Support for Scale-Degree Three of the Fundamental Line," Journal of Music Theory 34 (1990): 81-99.

⁶⁴As in conventional harmony textbooks of the past half-century such as Walter Piston's Harmony, (New York: W.W. Norton, 1945), which tells us (117) that the tonic six-four "is actually a dominant chord."

⁶⁵Burton Rosner and Eugene Narmour perpetuate the term dissonance for similar instances, but they do add the disclaimer contextual, which is a step in the right direction. See "Harmonic Closure: Music Theory and Perception," Music Perception 9 (1992): 383-412.

⁶⁶ If a more obvious trajectory was ever loaded into a phrase's first three measures (I - V - V6 ??? coupled with a 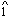- - 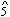- 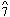??? bass line), I long to hear it. And herein lies one of the keys to structural clarity, not to say obviousness, embodied in music of Viennese classicism.

⁶⁷A detailed resumé of schematic expectation can be found in Bharucha, Ibid., 218-27.

⁶⁸Thom Clifton, Music As Heard (New Haven: Yale University Press, 1983), 23.

⁶⁹Without question, other properties are contributors, especially melodic contour. But I've chosen to deal with one thing at a time, and rhythm is the most powerful.

⁷⁰Rudolf Louis and Ludwig Thiulle, Harmonielehre (Stuttgart, 1907), 29: Diese Gebilde sind, isoliert betrachtet, durchaus konsonant. Aber der Zusammenhang, in dem sie auftreten, zwingt unsern Ohr eine Auffassung auf, in der sie tatsächlich als dissonant erscheinen.

⁷¹The authoritative (and perhaps seminal) statement of this view is found in two essays by Milton Babbitt, "Past and Present Concepts of the Nature and Limits of Music," in Perspectives on Contemporary Music Theory, eds. B. Boretz and E. T. Cone (New York: W. W. Norton, 1972), 3-9; and "The Structure and Function of Music Theory" in the same publication, 10-21. Babbitt's unquestioned authority for this "proof" has been invoked over the years, as in Norman Carey and David Clampitt's "Aspects of Well-Formed Scales," Music Theory Spectrum 11 (1989): 187, ¶ 2.

⁷²Michael Friedmann, Ear Training for Twentieth-Century Music (New Haven: Yale University Press, 1990), 69. Friedmann claims that pre-20th century conceptions of consonance and dissonance were nothing more than "linguistic rules established between the fifteenth and the eighteenth century." But if this be true, we must marvel that (among other things) the FCC chose the major 2nd for its Emergency Broadcast Signal. What makes that interval so universally effective in its tonally contextless function?

⁷³Although Norman Cazden found little sympathy for the ultra-rationalism of mid-century serialists, he shared their disdain for some of the conceptual alliances between acoustical data and music perception. His criticisms of the "overtone theorists" are often convincing; but then he forges ahead and throws out the wheat with the chaff in favor of a cultural determinism of experiential matters. Fully aware of the contradiction between qualitative states of sonance (Tonverschmelzung) and dynamic matters of stability and such, he nonetheless persisted in using the same words to describe the latter: They were contextually-determined sonances.

⁷⁴Babbitt, "The Function and Structure of Music Theory," 18-19.

⁷⁵A Generative Theory of Tonal Music (Cambridge, MA: MIT Press, 1983), 291.