For students interested in the analysis of the music of the Second Viennese School, or who are considering music theory as a profession, the study of atonal set theory, at least at an introductory level, would seem to be a prudent part of the undergraduate curriculum. Far less clear, however, is the case of students whose primary interests are remote from such matters. The music for which set theory was designed has increasingly become a smaller fraction of the 20th century repertory: new musical styles have developed and have flourished. In short, it may seem foolish to devote so much of a music student's class time to learn a difficult set theory that applies to a limited repertory.
I would agree with this argument, were it not that set theory, even at the elementary level, ought to be a general tool for learning about pitch structures, and not just applications limited to a particular repertory. An introduction to set theory should really be a kind of demystification, a way of efficiently showing that many properties of chords and scales are evident from their pitch content, and that those properties help to shape the music built from them. This, of course, is the kind of lesson that belongs in any academic curriculum.
The problem is that while standard set theory works adequately for those who already understand the tenets of set structure, it does not function well as a pedagogical tool. It represents musical ideas, but it rarely explains or demonstrates how to arrive at them. A statement like "set 4-11 is a subset of set 5-3" may well be concise, meaningful, and potentially useful, but it is not in a form that allows manipulation and study. The work needed to produce or even to verify that statement consists largely of consulting a table and a bit of trial and error—neither of which promotes thinking about music.
This is not the place for a general critique of the standard set theory.1 Rather, my goal is to show the pedagogical value of what I call "underground set theory," a simpler, though no less rigorous system that can encourage rational thought about the music our students encounter. It is used by a number of scholars and students, but it has rarely appeared in print and, unfortunately, does not appear in introductory music texts.2 Underground set theory is useful to the student from the start; it immediately shows a set's basic properties simply by the way the set is named. By using the following method, set class names may be generated directly from the set structure. Let us choose the chord A, F,  , and C.
, and C.
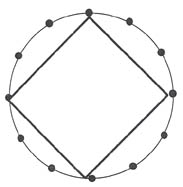
| Step 1. | Beginning on any note, list them in ascending order, allowing them to span no more than an octave. If we choose to begin on F, we order them F,  , A, C. Starting at F was arbitrary; ordering them A, C, F, , A, C. Starting at F was arbitrary; ordering them A, C, F,  , would work just as well. , would work just as well. |
| Step 2. | Find the distance in semitones between consecutive notes. Starting with the F, F up to  = 1 semitone, = 1 semitone,  -A = 3 semitones, A-C = 3, and C-F = 5. We return to F because we are in effect imagining the pitches on a circle, like a clock face, and counting the hours between them. See Example 1. -A = 3 semitones, A-C = 3, and C-F = 5. We return to F because we are in effect imagining the pitches on a circle, like a clock face, and counting the hours between them. See Example 1. |
| Step 3. | The set's name will be the largest number that can be produced through circular permutation, that is, starting on each note in the chord, and proceeding clockwise around the circle. Starting on F, the number is 1335. Starting on  , the number is 3351, and so on. Starting on C produces the largest number, 5133, and so we agree to call this set 5133. , the number is 3351, and so on. Starting on C produces the largest number, 5133, and so we agree to call this set 5133. |
Example 1: The set 5133.
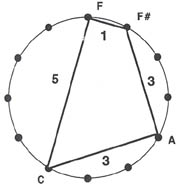
Using this method, all set names consist of digits adding up to 12 (e.g., 5+1+3+3 = 12), and the number of digits will equal the number of pitch classes in the set. Hence the four digit set name 5133 represents a tetrachord.
This means of naming sets makes unnecessary the cumbersome and offputting algorithms required for finding normal orders and a prime form. Each step in the above process is quite simple, not subject to error.
The first step collapses the chord into the span of an octave, which can even be done mechanically by placing the notes in alphabetical order. One need not search for the ordering that creates the smallest span (as one does in the standard algorithm); simply fitting the notes inside an octave is sufficient.
The second step measures the directed intervals in semitones between consecutive pitch classes.3 Intervals, not pitch classes, carry the information and form the basis of set classification. After all, two chords may be members of the same set class without sharing a single pitch class. Therefore, this step directly identifies the components that actually determine the set and its properties; pitch class integer notation such as (0, 3, 6, 9) does not. We may, of course, detect symmetry in the representation (0, 3, 6, 9 = the diminished seventh chord), but this is precisely because we are looking between the consecutive pitch classes and observing the recurring pattern of three semitones.
Pitch class integer notation allows all transpositions of a set to be written in the same way. That is to say, both (D, F, A) and (E, G, B) may be represented by (0, 3, 7). But since a set name based on directed intervals accomplishes this automatically, there is no need to change pitch letter names into integer notation.
This is a great advantage. Letter names are, after all, the normal way that musicians identify and talk about notes. It seems much easier to remember that, say,  -B is in a sense equal to A flat-B, and that both bear a similarity (harmonic) to D-F than to conjure up what "(8, 11)" sounds like. If one is programming a computer to examine or generate sets, then the use of integer notation will be useful. But, when using the underground system, standard note names may be retained with no loss of generality or precision.
-B is in a sense equal to A flat-B, and that both bear a similarity (harmonic) to D-F than to conjure up what "(8, 11)" sounds like. If one is programming a computer to examine or generate sets, then the use of integer notation will be useful. But, when using the underground system, standard note names may be retained with no loss of generality or precision.
To return to the naming process, the final step ensures that the set will have a canonical form, preventing the same set from having more than one acceptable, well-formed name.
The underground naming process is not wholly alien to students who have been taught to identify tonal chords. In the latter case, notes from the musical surface are similarly rearranged (stacked into thirds), as in our Step 1. The intervals between these newly arranged notes are then calculated, as in Step 2. The harmonic quality and root note that constitute a tertian chord's name are determined by the arrangement of intervals and the note on which the stack of thirds is built. In a set name, the sequence of intervals also plays a role in naming a chord, but rather than encrypt it into a common name, we keep the interval components "visible." So, Step 3 is vaguely like choosing the root, although there is no implication that the chord is somehow "built" or "generated" from a particular note.
Once sets are named and understood in this way, they stand ready to be studied and compared, and, more important, to be used as compositional or analytical tools.
Many academics have seen the value of annular (or "clock") diagrams in set theory, as mod 12 arithmetic represents the notions of octave and enharmonic equivalence.
By using directed intervals rather than interval classes in the naming of a set class, a chords and their inversions will not share the same set name in the underground system, as they do in the standard system. Their names will be related, however, as will be seen later.
Here, there is a happy correspondence between set name and the sides of the polygon inscribed in the circle of a clock diagram. This gives students an additional, geometrical way of understanding a chord and its name. The set 5133 is therefore a quadrilateral, and rotating the figure is analogous to transposing the set. The shape rotated 1 hour clockwise represents the set transposed up one semitone. The twelve possible orientations of this shape make evident how a set class (i.e., a particular shape) may exist at 12 transposition levels. (See Example 2.)
Example 2: The set 5133 at two transposition levels. The shaded version is the original set transposed by 1 semitone.
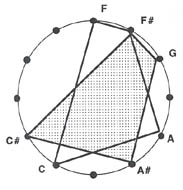
Relating transposition to annular rotation has the advantage of shifting the spatial metaphor of transposition (moving a set up or down) to rotating it clockwise or counterclockwise. The terms "up" and "down" naturally apply to register and contour; they necessarily suggest operations with pitches rather than notes (pitch classes). The concept of rotation is just as intuitive, but does not as easily tempt the student to think in terms of pitches and registers.
Teaching the concept of set inversion can be a thorny problem. One often feels obliged to use melodic contour to explain the idea, but then the connection between the two must eventually be disentangled.
It's best to avoid referring to melodic contour altogether by using indices of inversion. Once again, however, this may well be a useful construct for computer programmers writing algorithms for inversion calculations, but such abstraction is neither necessary nor helpful to the novice. It is far easier to note that, in a clock diagram, the inversion of a set is the mirror image of its inscribed polygon.4 One "flips" the polygon about any axis to produce the inversion. (See Example 3.)
Example 3: The set 5133 and its inversion, 5331.
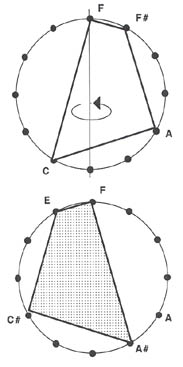
To find an inversion directly from a set name, one reads the set name backwards, then chooses the largest circular permutation (recall Step 3 of the original algorithm). For example, 5133 read backwards is 3315. By imagining 3315 to be a polygon inscribed in a circle, beginning on the "5" will produce 5331. This number ("five thousand, three hundred, thirty one") is the largest of the four possibilities.
Standard set theory would use set class 4-18 (0,1,4,7) to refer to 24 distinct sets: the 12 transpositions of 5133 and the 12 transpositions of 5331. It seems easier to understand that there is a strong aural and geometrical relationship between 5133 and 5331 (as inversionally related chords, they have the same interval vector) than to fathom why (0,1,4,7) is on the chart next to the name 4-18 because it is a "better normal order" than (0,3,6,7).5
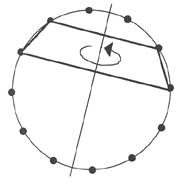
A set such as 7131 is inversion symmetric. This is to say, 7131 read backwards is 1317, which will be properly named 7131: the set inverts into itself. The standard set class name for 7131, 4-7(12), reflects this, for the 12 inversions are the same as the 12 original sets. Thus there are 12, not 24, members of set class 4-7(12). The set 7131 describes a trapezoid on a clock diagram, and its inversional symmetry is geometrically evident. (See Example 4.)
Example 4: The inversion symmetric set 7131.
As its set name illustrates, the diminished seventh chord (3333) inverts into itself. In addition, this chord also has the property of having fewer than 12 enharmonically distinct transpositions. This, too, is evident from the set name: 3333 may be generated by repeating the digit 3, indicating that there are only 3 transpositions. The whole tone hexachord (222222) and the augmented triad (444), occur in only two and four distinct transpositions, respectively. Any set name that can be completely generated by repeating a segment of itself will bear this property: the sum of the digits in the smallest segment will give the number of transpositions. The hexachord 313131 (6-20(4), historically the all-combinatorial "E" hexachord) therefore exists in only 4 transpositions, since the segment "31" repeats to generate the entire set name. The fact that there are only 6 enharmonically distinct French Sixth chords is evident from its set name, 4242. It is also, by inspection, inversion symmetric.6
The transpositional symmetry exhibited by these sets is also evident geometrically. The fact that there are only three 3333 sets is reflected in the fact that 3333 is a square, and that it only has 3 distinct orientations in the circle. If one transposes the set shown in Example 5 by 3 semitones, the square will apparently return to its original orientation. That is, transposition by a minor third has no effect on the pitch content of the chord. The following analogy makes this property clear: imagine the inscribed square made of cardboard and attached to the hour hand of a clock (with the base of the hour hand at the center of the square). Then, if one left the room and returned in three hours, the square would appear not to have moved.
Example 5: The diminished seventh chord 3333.
Hence, by considering the polygons representing the sets, students can see why certain sets behave this way. These geometrical analogies, as well as the fact that these set class names derive from what distinguishes them from other set classes (i.e., the intervals between consecutive elements), make this system far easier to teach. In short, the set properties are exhibited by the polygons, and, by extension, by the set names themselves.
Furthermore, these set names allow students to explore properties by enabling them to construct pitch collections that meet specified criteria. For example, one might be asked to construct an inversion symmetric pentachord in which there are no semitones or tritones. A student would then discover that the only such pentachord with these properties is the pentatonic scale (32322). One might also show that there are no pentachords for which there are fewer than 12 distinct transpositions, or that all transposition symmetric tetrachords are inversion symmetric. Such projects would help the student develop fluency in set manipulation and to think of pitch collections in terms of their properties and limitations.
Since the set class name represents intervals, it is no surprise that interval vectors can be calculated directly from a set name. One counts the instances in a set name of the numbers one through six, including those formed by adding consecutive digits that add up to six or less. Thus set 7131 contains two 1's, no 2's, one 3, two 4's (1+3 and 3+1), one 5 (1+3+1), and no 6's; its interval vector = [201210].
One must treat interval class 6 with special care, just as in calculating an interval vector directly from a standard set of pitch classes. In short, the number of times 6 occurs in a set name will be double the correct entry in the interval vector. Hence 6411 contains only one 6: its interval vector is [210111]. Students may either count the number of 6's in a set name and divide by 2, or realize that the 6 and the 411 in 6411 in fact represent the same tritone. The fact that 411 and the 6 represent the same tritone is also evident in the clock diagram. (See Example 6.)
Example 6: The set 6411, illustrating that the 6 and the 411 represent the same tritone.
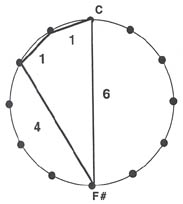
Determining the interval vector directly from the set name also gives the student easy access to a set's common tone properties under transposition. For example, interval vector [102111] for 5133 shows that for transposition up or down a semitone, a set will retain one pitch class. This is true because there is a 1 in the first column. The zero in the second column indicates that no pitch classes will be retained if the set is transposed up or down 2 semitones, and so on. As usual, one must exercise care in interpreting the sixth digit. In this case, it must be doubled, indicating that the set 5133 will retain 2 pitch classes if transposed a tritone.7
Perhaps the most useful feature of these set names is their ability to show subsets and supersets. Recall the tetrachord (F,  , A, C), which we found to be set 5133. Inspection of the pitch classes shows that the set contains an
, A, C), which we found to be set 5133. Inspection of the pitch classes shows that the set contains an  diminished triad as a trichordal subset. Note in Example 7 that the diminished triad is a triangle formed by eliminating one of the vertices of 5133.
diminished triad as a trichordal subset. Note in Example 7 that the diminished triad is a triangle formed by eliminating one of the vertices of 5133.
Example 7: The set 5133, illustrating the subset 633.
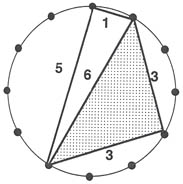
This is the same as "collapsing" consecutive numbers in a set name. That is, by adding together the 5 and 1 in 5133 produces 633, which is the diminished triad. In other words, given 5133, we can find its four trichordal subsets by inspection. They are: 633, 813, 543, and 651.8 Conversely, any superset of 5133 may be found by breaking any digit (or digits) into smaller numbers, which is analogous to adding more vertices to the inscribed polygon. Therefore, 5133 is a subset of hexachord 513111, in that the last digit (3) of the smaller set has been broken into (111).
One can also see that both 5133 and its inversion are subsets of the inversion symmetric hexachord 512121. Students could be asked to prove the general case that if Set A is a subset of an inversion symmetric Set B, then the inversion of Set A is also a subset.
The level of abstraction (and the degree of formality) with which a particular student confronts this or similar problems will vary from course to course. The experience of dealing with pitch relationships in a logical matter in abstract ways makes a useful lesson for music students at any collegiate level of instruction.
Finally, if the same subset fits into the larger set at more than one transposition level, this will be reflected in the number of different ways the larger set can accommodate the digits of the smaller. So 512121 will contain the tetrachord 8121 twice, since the larger set may accommodate 8121 in these two ways: beginning with the five ((5+1+2) 1 2 1) and beginning with the second two ((2+1+5) 1 2 1).
Once again, unlike in the standard system, the underground system is a way of calculating and predicting relationships, not just representing them. One can see whether a given set is a potential subset of another (through transposition or inversion) by generating and inspecting the set names. By solving a problem—such as finding the largest common subset between the diatonic and octatonic collections—students discover abstract properties as well as develop manipulative skills useful to analysis.9 For example, one could note that the dominant seventh chord (4332) and the whole tone chord (222222) share a trichordal subset 624. This suggests that such a sonority could play a crucial role in music that explores the relationship between the diatonic and whole tone systems. Such is the case in the Prelude to "The Afternoon of a Faun," where, in measures 8-10, for example, a 624 may be heard as part of a dominant seventh chord based on B-flat or as part of a whole tone pentachord.
A look at the subsets of the diatonic set itself (2221221) is particularly instructive. Students can show that it contains 3 major triads, 3 minor triads, one diminished triad, but no diminished seventh chords or augmented triads. This is because the major triad (543) and the minor triad (534) each appear three times each, but the diminished triad (633) appears only once. There is no way to produce either 3333 or 444, so the diminished seventh and the augmented triad are absent. The dominant seventh chord, or "major-minor seventh" chord (4332) may be shown to appear once, while the inversion symmetric minor seventh chord (4323) appears three times.
All this information about the diatonic collection will probably already be known to the student. The point about the underground system is that this information can be arrived at simply and shown in the manner of a proof.
Moreover, while we have many years to internalize the properties of the diatonic system, we generally are more pressed for time when learning about such scales as the octatonic or whole tone, let alone even more exotic collections. This system enables students to call upon set theory as a means for extracting properties derivable from unfamiliar collections.
For instance, consider the octatonic set 21212121, the polygon for which is shown in Example 8. Inspection of the set name shows that it is inversion symmetric: there are only 3 distinct transpositions of the set. The symmetry evident in the polygon suggests a number of other properties: we expect, for example, that particular subsets will occur fourfold, since each feature of the polygon appears identically 4 times. Within the octatonic set, the major triad appears 4 times, as does its intervallic inversion, the minor triad. The diminished triad appears 8 times, however, due to its inversional symmetry. That is, the set 633 appears 4 times, while its inversion (which also happens to be 633) appears 4 times as well. This makes a total of 8. The relationship between the diminished seventh chord and the octatonic set could be explored by the student in a similar way.
Example 8: The Octatonic Set 21212121 with subsets: major triad 543 and diminished triad 633.
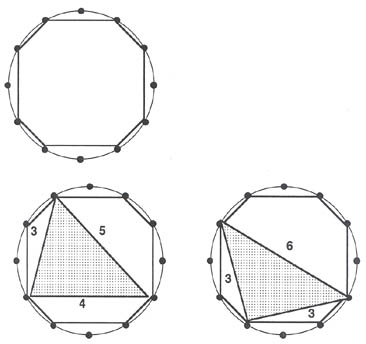
There are some important consequences of these properties. Since there are a total of 12 enharmonically distinct major triads in the universe of 12 pitch classes, and each of the 3 octatonic sets contains 4 of them, we may deduce that the 3 octatonic sets share no major triads, and, equivalently, a given major triad will determine a particular octatonic set. The same is true for the minor triad.
On the other hand, since there are 12 enharmonically distinct diminished triads in the universe of 12 pitch classes, and since each of the 3 octatonic sets contains 8 of them, we may deduce that any 2 octatonic sets share 4 diminished triads, and, equivalently, a given diminished triad will occur in two of the three octatonic sets. In an interesting way, this relationship between major and diminished triads in the octatonic system mirrors that in the diatonic system: while 633 determines a particular collection (key) in the diatonic system, it is a common chord in the octatonic system. Conversely, the major triad determines a "key" in the octatonic system, while it is a common chord in the diatonic system.
After deriving this and other information from the octatonic set, students could explore to what extent these properties shape octatonic pieces or passages. For example, one could also fruitfully compare the interval vector of the diatonic set [254361] with that of the octatonic set [448444]. We see a startling difference in the properties of these sets on transposition. Because each entry in the interval vector is unique, the diatonic collection enjoys the greatest variety in number of pitches retained upon transposition: from 2 to 6, as indicated by the interval vector.10 Hence, each modulation will have its own characteristic sound: some keys are closely related, and some are remote. By contrast, in the octatonic system, all modulations either retain a diminished seventh chord, or keep all eight notes.11
We have seen how clocks and set names create a medium through which pitch and set relations can be explored. Like all analytical representations, these clarify certain attributes while disguising others. Students should be shown that an analytical representation is often altered in order to bring a different parameter or property into focus.
For example, by representing the diatonic collection as 2221221, we obscure its relationship to the circle of fifths. Let us therefore modify our clock diagram to make that relationship explicit. Consider the diatonic set to be a polygon on a clock where consecutive hours represent pitch classes in the order of a circle of fifths rather than in the chromatic order we have used thus far. In this way, many important properties of the diatonic system will become graphically evident.
The diatonic set is now represented by 6111111, as illustrated in Example 9. Since all 7 elements of the set are consecutive elements in the circle of fifths, we may simplify the presentation even further by transforming the circular diagram into a linear one. Here, the rectangle represents a diatonic collection. Example 9 shows rectangles representing the keys of C major, F major and the 6 pitch classes they have in common.
Example 9: The diatonic set as a series of 7 consecutive perfect fifths.
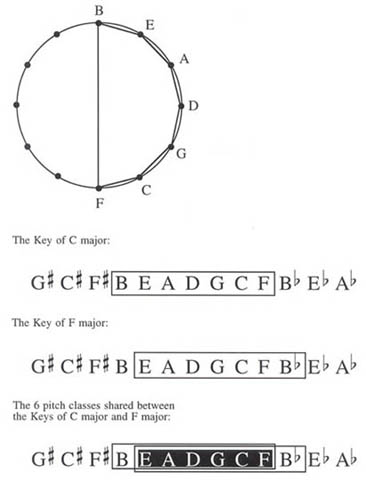
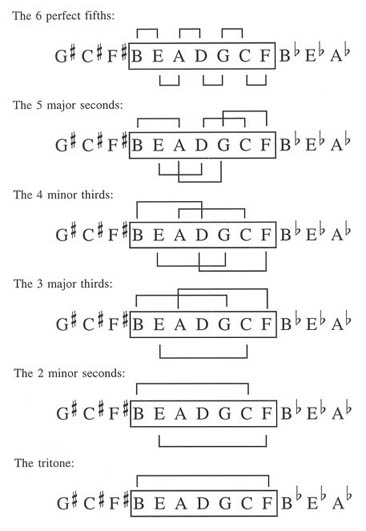
Note that since consecutive elements create perfect fifths (or fourths), the rectangle (which contains 7 elements) can encompass 6 of these intervals. The interval created by elements 2 fifths apart is the major second, and the rectangle can therefore accommodate 5 of these. A distance of 3 fifths yields a minor third, and only 4 of those fit in the rectangle, and so on. This illustrates that the unique value of each entry in the interval vector [254361] results from grouping together 7 consecutive elements in the circle of fifths. (See Example 10.)
Example 10: Intervals in the Key of C major:
Intervals shared between the Key of C major and the Key of F major:
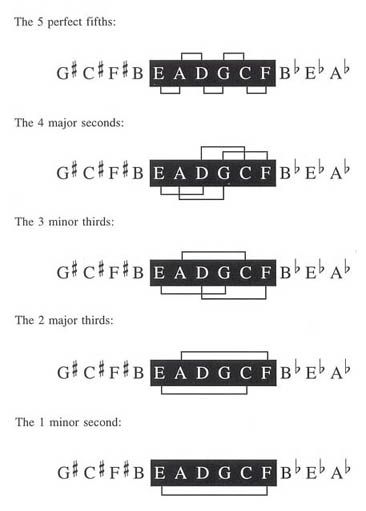
To move from the C major collection to the F major collection we shift the rectangle one step to the right. As we should expect, we lose the B-natural and gain the B-flat. We also lose one instance of each interval. That is to say, we lose one perfect fifth (B-E), one major second (B-A), and so on.12
Further, if we move to the key of B-flat from the key of C, we now lose 2 pitch classes as well as 2 of each interval. In short, using this model for modulation we can see precisely how intervals are lost or retained as one travels to more distant keys.
The general case is shown in Example 11.13 The example uses interval vectors to tally the intervals shared between the original key (here, C major) and the other major keys. In other words, the hexachord in common between the keys of C major and G major (322122) has the interval vector [143250], each interval occurring once less often than in the original [254361]. The pattern continues smoothly through the keys until finally, at the most remote point, the tritone reappears as the only common interval [000001].
Example 11: Chart illustrating common subsets (and their interval vectors) between the Key of C major and its transpositions (the other major keys), as arranged by circle of fifths.

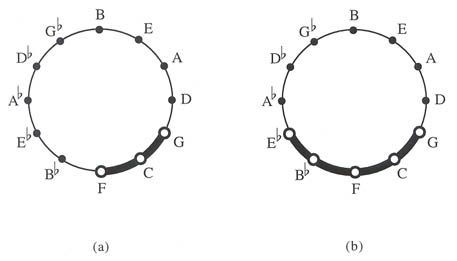
Using set names and diagrams in this way, many properties of the diatonic set that play crucial roles in tonal music become evident. With the exception of the tritone, each particular interval can only be shared by keys consecutive on the circle. For example, the major second C-D exists in the keys of G, C, F, B-flat and E-flat major, which appear consecutively on the circle of fifths. Triads are also shared in this orderly manner. (See Example 12.)
Example 12:
(a) Diatonic sets containing the C major triad.
(b) Diatonic sets containing the major second C-D.
Ultimately, the steady pattern in the attrition of intervals and triads illustrated in Examples 11 and 12 makes possible the regular heirarchy of key relationships, from "closely related" to "remote," so crucial to the tonal system. An interval that is "lost" when one modulates from the key of C major to D major will not return if one modulates to the more distant key of A major.
The fact that the tritone entry in the interval vectors in Example 11 is empty except in the case where it is the only common interval is also related to many characteristics of the tonal music. It means, for example, that a tritone plus any note will determine a major key. This in turn means that the V7 chord supplies all the information needed to tonicize the triad whose root is a perfect fifth below.
It also shows one reason why such progressions as IV-V-I and ii-V-I work so efficiently: IV or ii will inevitably provide scale degree 4, while V will contribute scale degree 7. Hence, by the time the tonic chord is stated (or elided), these chords will have spelled out the key.
It also means that there are only 6 enharmonically distinct tritones, since there are only 12 major keys, and each major key shares its one tritone with one other key. Of course, one does not need sets and diagrams to show that there are only 6 tritones. But the point remains that with these tools, one can see the relationships between the interesting properties of the diatonic sets, and that is indeed worth exploring, whether one is interested in tonal, post tonal, or any music where the notion of pitch class plays a significant part.
The lesson that understanding the structure of a phenomenon goes a long way toward understanding its properties (and that the diatonic system is one case in point) is, of course, the primary role of set theory as presented here. However, there is another important lesson that set theory can make clear to students.
As central as diatonic structure is to traditional tonality, there is far more to the language than can be gleaned directly from the diatonic set, even from a purely structural point of view. For one thing, there are characteristics of tonal music that apparently contradict what is suggested by the structure of 2221221. Consider that it is evident from the set name that there is an axis of inversional symmetry that runs through the diatonic set. For the collection defining the key of C major, this axis passes through pitch classes D and  .14 Because C and E lie at analogous points on either side of the axis, some kind of equivalence between these two pitch classes (in general, the tonic and mediant), would seem to be predicted.
.14 Because C and E lie at analogous points on either side of the axis, some kind of equivalence between these two pitch classes (in general, the tonic and mediant), would seem to be predicted.
Indeed there necessarily are some similarities between the roles of tonic and mediant in a major key. Both, for example, are members of the only triads that do not contain members of the tritone of the key (I and vi), and both serve as points of resolution for that tritone. Still, one can hardly characterize their roles as equivalent in practice.15 Hence, in this case, practice overrides the equivalence suggested by set structure.
More important, however, is that the set 2221221, as basic as it is to tonal music, is not the only source set in that music. The harmonic minor and (ascending) melodic minor collections occur with great frequency and normalcy, and play a fundamental role in tonal music. As 3121221 and 2222121, respectively, they are similar enough to 2221221 to be heard as variants. Yet their stuctures endow them with quite different properties, as their interval vectors ([335442] and [254442]) demonstrate.16
For example, neither set produces the regular patterns of retention and attrition associated with 2221221 and illustrated in Examples 11 and 12. Example 13 shows the common subsets between the C harmonic minor collection and its transpositions: the pattern is much less regular, whether measured as a function of distance in perfect fifths or in semitones. Example 14 shows similar behavior for the C melodic minor collection under transposition.17 Indeed, closeness and remoteness are not so convincingly (or perhaps meaningfully) measured among these sets.
Example 13: Chart illustrating sets and interval classes retained as the harmonic minor collection (3121221) is transposed by interval class 5 or by interval class 1.
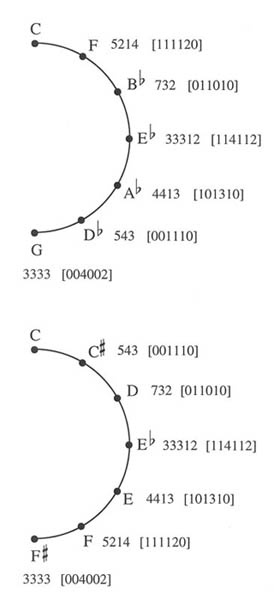
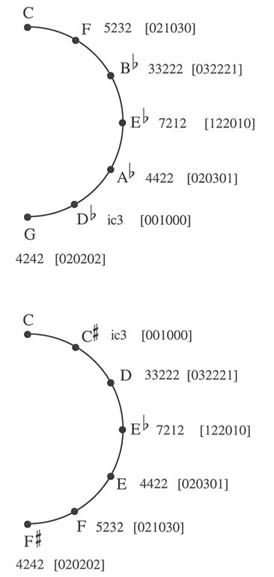
Example 14: Chart illustrating sets and interval classes retained as the melodic minor collection (2222121) is transposed by interval class 5 or by interval class 1.
To illustrate, let us consider the C harmonic minor collection as the starting point in the first circle in Example 13. In terms of subset cardinality, we see that the F and B-flat harmonic minor collections are progressively more remote from the C collection, as they share with the original set a tetrachord (5214) and trichord (732), respectively, and the common intervals decrease from [111120] to [011010]. But, if we proceed to the E-flat collection, we are startled to find a common pentachord (33312), the maximum common subset. We also retrieve intervals that were previously lost (most notably the minor thirds and tritones). A look ahead to the A-flat collection reveals that while we return to the smaller, common tetrachordal subset (4413), we reach the maximum number of common major thirds (3). This staggering of maxima took place only once in the major scale, with the exceptional, sudden return of the tritone at a transposition of six perfect fifths. Here, it is the norm.
If we instead wish to gauge closeness in terms of shared triads, we see that the only collections that share no triads with the C harmonic minor collecion are the B-flat and (by symmetry) the D collection, only 2 steps away in the circle. Furthermore, sharing a major triad turns out to be characteristic only of harmonic minor collections a semitone apart, almost the furthest distance on the circle of fifths. In that case, those are the only pitch classes shared.18 Finally, we note that since the diminished seventh chord (3333) is a subset of the harmonic minor collection, each transposition of the harmonic minor scale by a minor third will retain that diminished seventh chord. Therefore, each of the 12 harmonic minor scales may be categorized according to which of the three diminished seventh chords it contains. This means that a diminished seventh chord may act as a pivot chord among four harmonic minor collections, the tonic notes of which form a 3333.19
These observations demonstrate how the structure of the harmonic minor collection yields properties under transposition quite unlike those of the major scale. As one expects, the melodic minor collection behaves in yet different ways, as a study of Example 14 would illustrate.
Indeed, the harmonic and melodic minor collections thus enrich the tonal system by contributing their own peculiar properties, and one such property is the less straightforward way in which these collections retain pitch classes and chords. A next step in this study would be to examine how various transpositions of, say, the harmonic minor collection effect its relationship to the major scale, and so on. Such explorations are indeed quite valuable for any student of tonality.
Our brief look at the structure of these collections has barely touched on what accounts for what we experience in tonal music. On the contrary, while the properties evident in set structure certainly play a crucial role in music using these sets, they by no means completely predict or determine the musical results.
This is the second important lesson that set theory offers students. Diatonic set structure is the starting point for common practice tonality; it is a kind of genetic code that creates the potential for the musical system that will develop and evolve. Some properties of tonality are predetermined by diatonic structure (for example, the ability to create a plausible heirarchy of major keys). On the other hand, some aspects of the system, while certainly made possible by diatonic set structure, are highly developed and far removed from a simple applications of a set's property. Finally, like any theoretical system, set theory simplifies the object in order to bring otherwise hidden properties into relief.
Consider, for example, the musical sophistication brought to tonal voice-leading by the common practice masters. The potential for interesting voice-leading is greatly enhanced by the structure of the diatonic collection. It provides, as a start, two distinct, but simply related, diatonic steps (major and minor seconds), and a potential ambiguity between the augmented step and the smallest common skip, the minor third. Yet, harmonic syntax is a controlling factor in voice-leading, and it would be absurd to claim that all the subtleties of tonal syntax are clearly present in embryonic form in the major scale.
When we study pitch organization based on other collections, we should expect a similar situation. Understanding the properties of a source set and of other important sets in a composition is an important theoretical step. But, as in the case of tonality, set structure ultimately determines the potential for the ensuing musical language, while the work itself will tell what path its composer has chosen to explore.
A study of musical set theory gives student the means to efficiently discover and explore the structures whose properties shape a musical language. At the same time, one discovers that compositional invention (whether it be in a single work, or in the development of a style) finds fresh ways to use and transform these properties. By making the investigation of set structure practical, set theory encourages students to think of their musical language in a logical, demystified way.
1One may take as the basis for standard set theory Allen Forte's The Structure of Atonal Music (New Haven: Yale University Press, 1973), the book that introduced many musicians to atonal set theory. Although it precipitated several reviews that were critical of the system even at the outset, the system (or a close relative) is now standard. Indeed, it is not difficult today to find essays that use the system that neither cite Forte's book nor offer an explanation of the nomenclature.
Over the years, scholars have made improvements in the system. For example, the term "set class," now often used to distinguish the general configuration (0, 1, 2) from a specific pitch class "set" (such as F,  , G), does not appear in Forte's book.
, G), does not appear in Forte's book.
2The system described here combines a numerical system with one based on clock diagrams. The numerical system may be most conveniently found in Eric Regener, "On Allen Forte's Theory of Chords," Perspectives of New Music 13 (1974): 191-212. It is also described in Richard A. Chrisman, "A Theory of Axis-Tonality for Twentieth Century Music," Ph.D. dissertation, Yale University, 1969. Clock diagrams are used extensively in Harold Lewin, "On the Formation of Collections of Twelve-note Rows that Contain Segments of Common PC Content," College Music Symposium 20:1 (Spring, 1980): pp. 49-92.
3The distances between set elements derived in Step 2 are not interval classes, since, for one thing, they can be larger than 6. Regener calls them "directed intervals," as they are always calculated clockwise on the circle (op. cit., p. 193).
4This is not to say that inversional indices and other numerical processes circumvented in this essay should not be learned and understood. On the contrary, they belong at a later stage of an introductory course, or in a more specialized course. Avoiding them at an elementary stage makes set manipulation more accessible and intuitive (and inviting) to more students.
5It is true that our system also has arbitrary preferences, such as in choosing the name 5133 over 1335, but, given the number 1335, the preferred name is determined by simple inspection. Realizing that (0,3,6,7) is better represented by (0,1,4,7) is far more complicated.
6The only sets that are transposition symmetric, but not inversionally symmetric, are the hexachords 321321 and 312312. The proof is left to the reader.
7If a set is transposed by a tritone, any tritone it contains will remain, as one note in the tritone will become the other, and vice versa. Therefore, a 1 in column 6 indicates that two notes will be retained.
8It should be clear that the last and first digits of the set name are consecutive, as one may start anywhere on the inscribed polygon. Therefore, the set 5133 contains 813, since the last 3 and the 5 are consecutive.
9Although both these terms may have other meanings, in this essay we use diatonic collection to mean the major scale. Octatonic collection refers to the set 21212121.
10The 1 in the last column indicates that 2 pitch classes are retained if the set is transposed a tritone (e.g. modulation from the key of C major to  major). In that case, the retained pitches will form a tritone. The 2 notes retained upon transposition of 1 semitone (e.g. modulation from the key of C major to either the key of B major or
major). In that case, the retained pitches will form a tritone. The 2 notes retained upon transposition of 1 semitone (e.g. modulation from the key of C major to either the key of B major or  major) will form interval class 5.
major) will form interval class 5.
11The interval vector [448444] indicates that all transpositions retain 4 pitch classes except T = 3, 9 (represented by column 3) and 6 (represented by column 6), where all 8 are retained.
12Of course, new instances of each interval arise to take their places. The perfect fifth B- is replaced by F-B-flat, the major second B-A is replaced by C-B-flat, and so forth.
is replaced by F-B-flat, the major second B-A is replaced by C-B-flat, and so forth.
13I wish to thank Brian McCartin for this diagram.
14One may observe this symmetry in the diatonic polygon inscribed either on a clock where the hours are ordered chromatically or one ordered by circle of fifths.
15This equivalence has come in handy in speculative theory, however. Moritz Hauptmann's theory of harmony, which is founded on the symmetries of the diatonic system, shows a fundamental relationship between the roles of these scale degrees. C is the generator of the tonic triad in the key of C major, while E is the generator of the tonic triad in the relative key of A minor. See Moritz Hauptmann, The Nature of Harmony and Metre, trans. William Edward Heathcote (New York: Da Capo Press, 1989), p. 17.
16The major and melodic minor scales are inversion symmetric: both 2221221 and 2222121 invert into themselves. Harmonic minor, 3121221, however, inverts to become 3122121, which was once known as the harmonic major collection. See, for example, Nikolai Rimsky-Korsakov, Practical Manual of Harmony, trans. Joseph Achron (New York: Carl Fischer Press, 1930), p. 6.
17I am using the term "melodic minor collection" to refer to pitches from the ascending melodic minor scale.
18The simplest way to predict under which transpositions an interval (or chord) will be retained is to observe the scale degrees in the original set on which that interval may be built. For example, in the major scale, minor thirds can occur only above scale degrees 2, 3, 6, and 7. Hence, the minor third A-C may only occur in G, F, C, and B-flat major: that is, where pitch class A is scale degree 2, 3, 6, or 7, respectively. In the harmonic minor scale, minor thirds are built on 1, 2, 4, 6 (as the enharmonically equivalent augmented second), and 7. This means that A-C is to be found in harmonic minor collections based on A, G, E,  , and B-flat.
, and B-flat.
19For example, a  diminished seventh chord may act as pivot from the key of A harmonic minor to the keys of C, E-flat, and G-flat. (In practice, these may be major or minor keys.)
diminished seventh chord may act as pivot from the key of A harmonic minor to the keys of C, E-flat, and G-flat. (In practice, these may be major or minor keys.)



