Scholars often approach the study of twentieth-century music by distributing it into a number of schools or isms. As a result, we have become accustomed to labeling twentieth-century music in terms of stylistic categories such as impressionism, expressionism, and primitivism to name just a few. This traditionally segregated approach to the examination of twentieth-century music can be very worthwhile if our interests lie in exploring the various philosophical, historical, and aesthetic precepts leading to the development of the different compositional schools. Through such approaches, for instance, we can observe the intense interactions between society and art manifested in the works of composers willing to risk their reputations, and even their livelihoods, for the advancement of artistic freedom and expression. And, the very nature of these same compositional schools often makes it easy for us to construct analytical approaches that closely coincide with the processes employed by composers.
Yet, something is missing from this view. When attempting to teach musicians how to hear such works, the isms often seem to get in the way. After all, the majority of composers working during the past century relied to a great extent upon the same basic musical building blocks employed for many centuries regardless of the particular stylistic approach they used. By shifting our analytical vantage point, we can begin to see that a conceptualized world of discrete schools might actually be viewed quite productively as a set of variations on a few common themes. It is precisely this aspect of twentieth-century music that we wish to explore, namely how twentieth-century compositions representative of a variety of schools can be analyzed on the basis of certain common musical threads or basic compositional building blocks. Repositioning our analytical inquiry in this way allows us to approach the problem of how to understand and hear twentieth-century music in a much more concise manner; that is, by learning to recognize one set of common elements and their variants rather than struggling with all the complex demands inherent in having to learn the structural and aural nuances of a plethora of isms.
In this article, we advocate a return to analysis based on ordered motives long advocated by such theorists as William Benjamin, Jonathan Bernard, and Richmond Browne.1 Building on the ideas of these theorists, we propose an approach to analysis and aural skills that emphasizes germinal melodic ideas, ideas that form the basis for musical organization within individual pieces, yet transcend the boundaries of the various isms and schools. We will refer to these germinal ideas as motives. While motives can take on a number of different forms ranging from abstract ideas to highly-prescribed pitch/rhythm designs, defining motives according to shape (contour) and intervallic content alone produces quite rich results when applied analytically and aurally to twentieth-century music. We have found, for instance, when we concentrate on relatively short shape/interval motives (often consisting of only three or four pitches) along with their ordered transformations, we are able to account for important details in the music of a number of important composers, including Messiaen, Ives, Debussy, Shostakovich, Copland, Rorem, Crawford, Schoenberg, Scriabin, Bartók, Webern, Stravinsky, Hindemith, and Crumb.2 Other aspects of music—pitch and rhythm, for instance—help to establish context and thus serve primarily to highlight motives defined by shape and intervallic content in this model.
While incorporating some of the operations used in pitch-class set theory, our method differs from traditional applications of set theory in that it de-emphasizes unordering.3 Unordered motives when they do occur can often be accounted for through rotation or through the combination of unordered and ordered transformations resulting in hybrid forms of a motive. Motivic analysis based on ordered operations cannot, of course, account for all aspects of twentieth-century music. As the analyses in this paper suggest, however, conceptualizing twentieth-century music motivically may lead to satisfying analytical insights into music representative of a wide variety of styles (insights that are also aurally accessible) because such an approach enables us to look at individual compositions as being essentially unique variations of a common technique.
Ordered Shape/Interval Motives and Their Transformations
Example 1 displays several excerpts along with their principal pitch patterns and transformations. Arrows in the example indicate a change of contour. As the bracketed groupings above the staff in Ex.1a illustrate, the principal pitch-motive in Messiaen's Quatuor pour la fin du temps, movement 6—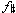 '-e'-
'-e'-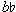 '—recurs several times in the first four measures where its first pitch receives both metrical and agogic emphasis. Focusing on the intervals and contours of this gesture brings a number of other motivic constructions into play, including, most particularly, the transposed inversion (I) of the original pitch-motive,
'—recurs several times in the first four measures where its first pitch receives both metrical and agogic emphasis. Focusing on the intervals and contours of this gesture brings a number of other motivic constructions into play, including, most particularly, the transposed inversion (I) of the original pitch-motive, 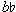 '-c''-
'-c''-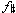 '. This intervallic contour too occurs numerous times throughout the passage as the brackets beneath the staff indicate. Indeed, the original pitch motive, together with its inversion, form a chain of motives—some of whose pitches overlap—that subsumes nearly every pitch in the passage. Measure 3 contains two motives, one of which is the retrograde inversion (RI) with a change of contour. This motive contains the same intervals as the transposed retrograde inversion (notated with small note-heads beneath the staff), but replaces the expected descending major second,
'. This intervallic contour too occurs numerous times throughout the passage as the brackets beneath the staff indicate. Indeed, the original pitch motive, together with its inversion, form a chain of motives—some of whose pitches overlap—that subsumes nearly every pitch in the passage. Measure 3 contains two motives, one of which is the retrograde inversion (RI) with a change of contour. This motive contains the same intervals as the transposed retrograde inversion (notated with small note-heads beneath the staff), but replaces the expected descending major second, 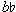 '-
'-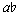 ', with an ascent of the same distance. Measure 4 contains two bracketed motives in which the notes of one motive are interpolated between those of another, more global, motive. Example 1a also contains what may be considered two non-motivic pitches,
', with an ascent of the same distance. Measure 4 contains two bracketed motives in which the notes of one motive are interpolated between those of another, more global, motive. Example 1a also contains what may be considered two non-motivic pitches, 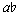 ' and
' and 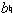 '. These pitches elaborate motivic pitches in a manner similar to elaborative figures in tonal music;
'. These pitches elaborate motivic pitches in a manner similar to elaborative figures in tonal music; 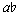 ' forms an arpeggiation with c' and
' forms an arpeggiation with c' and 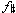 ' while
' while 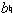 ' is the chromatic upper neighbor of
' is the chromatic upper neighbor of 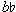 '. Similar relations between motives—twelve-tone operations such as inversion (I) and retrogression (R), overlapping pitches, shape alterations, and an octave shift—also occur in the excerpts from Webern's String Quartet, Op. 5, mvt. 3 and Bartók's String Quartet No. 3, as illustrated in Examples 1b and 1c.
'. Similar relations between motives—twelve-tone operations such as inversion (I) and retrogression (R), overlapping pitches, shape alterations, and an octave shift—also occur in the excerpts from Webern's String Quartet, Op. 5, mvt. 3 and Bartók's String Quartet No. 3, as illustrated in Examples 1b and 1c.
Example 1a. Messiaen, Quatuor pour la fin du temps, mvt. 6; Principal Motive and Transformations.

Example 1b. Webern, Five Pieces for String Quartet, Op. 5, mvt. 3; Principal Motive and Transformations.

Example 1c. Bartók, String Quartet No. 3, mvt. 1; Principal Motive and Transformations.

The three excerpts in Ex. 1 differ from each other stylistically, but parse equally well when analyzed in terms of ordered pitch intervals and contour. That intervals and contour are fundamental to our understanding of music has been aptly demonstrated by a number of researchers including William J. Dowling and Diane S. Fujitani (1971), Lucinda A. DeWitt and Robert J. Crowder (1986), and Judy Edworthy (1985). Not surprisingly, these researchers have found that subjects respond most immediately to contour when listening to music. On the other hand, as DeWitt and Crowder have observed, intervallic information may be more difficult to apprehend initially, but appears to emerge better than contour information after longer time delays.4 This suggests that despite the accessibility of contour, intervallic content also plays an important role in melodic structuring and may even surpass contour where the recognition of familiar melodies is concerned. Building on these observations, we propose an abstract melodic entity that incorporates intervals and contour into a single ordered shape/interval motive. Such a motive can be used as the foundation for analysis inclusive of many styles and genres precisely because it engages certain cognitive primitives basic to musical understanding.
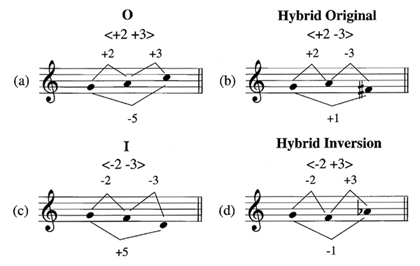
Example 2 shows an original (O) three-note shape/interval motive consisting of an ascent of five semitones followed by an ascent of two semitones. The two separate aspects of the figure—shape and intervallic content—can be combined into a single argument using ordered pitch intervals where the signs + and - indicate ascents and descents respectively and Arabic numerals indicate intervallic sizes measured in semitones. Using this approach, the motive in Ex. 2 may be expressed as the ordered pitch-interval set <+5 +2>.5 Shape/interval motives, thus defined, are ordered and may be subjected to ordered operations such as inversion (I), retrograde (R), and retrograde inversion (RI) as illustrated in the example.
Example 2.
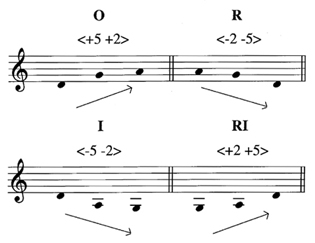
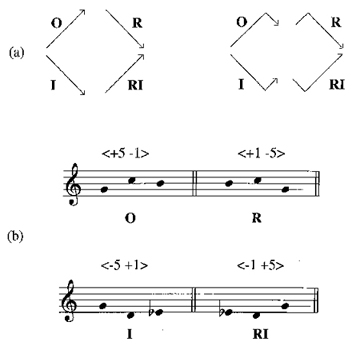
Where ordered motives are concerned, shape in association with register alone can be a strong indicator of retrograde and inversion. Extrapolating from Ex. 2, for instance, we find that when the original motive outlines an ascent, the inversion and retrograde will always outline a descent; the retrograde inversion, reciprocally, will outline an ascent, just as the original does. The inversion and retrograde inversion, furthermore, open up a new register. Understood in terms of shape and register, then, the inversion mirrors the shape of the original in a new register while the retrograde reverses the shape of the original in the same register. This principle applies not only to smooth contours like those in Ex. 2, but also to jagged contours. Example 3a isolates a few shapes using line drawings to illustrate the relations between them. In these drawings, intervals are unspecified aside from the fact that the second interval in the jagged motives is smaller than the first. This information is all that is needed to accurately identify relations between motivic shapes. The transformations of the original motive in Ex. 3b, for instance, can be easily determined without taking into account their specific intervallic content; the original and retrograde shapes extend above g', while the inversion and retrograde inversion extend below g'.6
Example 3.
Parsing music into shape/interval motives is primarily a grouping activity; shape/interval motives, that is, stand out in the texture because their ordered pitch intervals—and sometimes the pitches that outline those intervals—form repetitive clusters. The melody in Ex. 4a, for instance, contains an untransposed three-note grouping that occurs only three times in the passage. The excerpt in Ex. 4b is somewhat more complex in that it contains transposed motives.7 The melodies in Examples 5a and 5b are similar to those in Ex. 4, except that they include twelve-tone operations such as inversion, retrogression, and retrograde inversion.
Example 4.
Ned Rorem, Poems pour la paix, Sonnet, mm. 4-9.

Scriabin, Prelude, Op. 74, no. 3, mm. 9-12.

Example 5.
Bartók, Mikrokosmos, No. 91, Chromatic Invention, mm. 1-8.

Crawford, Diaphonic Suite No. 1 for Solo Flute or Oboe, mm. 1-13.

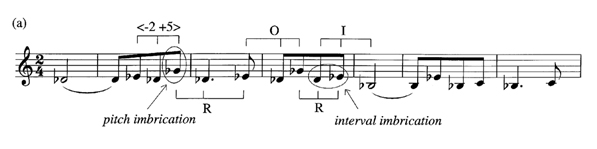
Central to the understanding of ordered motives are the transformations used to expand them into large-scale melodic gestures. Of these, chains of overlapping motives are among the most common. There are two main types of overlapping motives; those with imbricated or shared pitches and those in which the pitches of one motive are interpolated or inserted between the pitches of another.8 Because the number of overlapping pitches has important consequences where shape is concerned, we will further distinguish between imbricated motives that share one pitch and imbricated motives that share two or more pitches, referring to the latter technique as interval imbrication and the former as pitch imbrication. This distinction is necessary because whereas any two motives with any ordering may share one pitch (the only stipulation being that the last pitch of the first motive overlap with the first pitch of the second motive), the number of possible motivic combinations decreases sharply when more than one pitch overlaps. This is because in order to share two pitches, both imbricated motives must also share an interval along with its attendant shape.
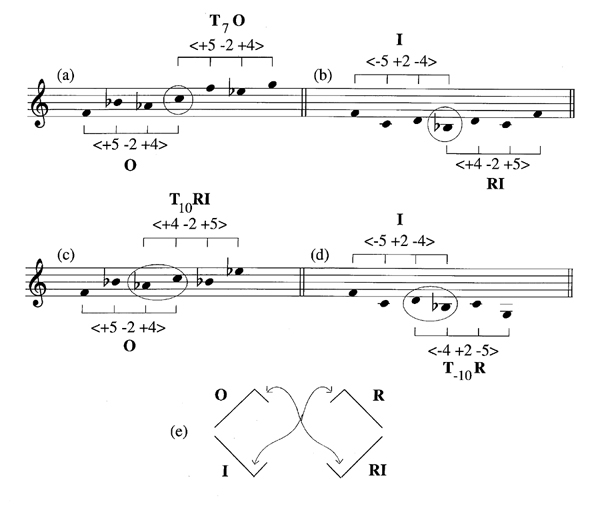
Example 6 shows a few sample motives imbricated either by pitch or interval. Imbricated pitches are circled in the example. The melodic sequence in Ex. 6a contains two motives imbricated by pitch where the second motive is transposed seven semitones in order to allow its first pitch to overlap with the last pitch of the original. In Ex. 6b, the inversion of the original motive is imbricated by pitch with the retrograde inversion, which does not need to be transposed in this case because the imbricated first note of the retrograde coincides with the last note of the inversion. The motives in Examples 6c and 6d are imbricated by interval. In the first of these examples, the initial bracketed shape is the original motive while the second is the retrograde inversion transposed ten semitones. The imbricated pair in Ex. 6d, on the other hand, consists of the inversion and the retrograde transposed down ten semitones. These pairings will always arise when motives are imbricated by interval. That is, where interval imbrication is employed, the original will only interface with its retrograde inversion while the inversion will only interface with the retrograde and vice versa. The line drawings in Ex. 6e illustrate why this situation arises. The final interval of the original only occurs at the beginning of the retrograde forms, but is upside down in the retrograde. Inversion, in this case, has the effect of rotating the upside down shape in the retrograde to the front of the motive so that it matches the shape of the final interval in the original.9 The transpositions of these unique permutations, moreover, will always be inversions of each other; in Examples 6c and d, for instance, the retrograde inversion is transposed up ten semitones while the retrograde is transposed down ten semitones.
Example 6.
Unlike the pitches of imbricated motives, interpolated pitches may be either motivic or non-motivic. In either case, interpolated pitches serve as a means of elaboration. In this discussion, we will emphasize motivic interpolations. In addition, we will differentiate between interpolation in which all the notes of an interpolated motive occur within the span of a larger motive and interpolations with imbrication in which some of the notes of the two motives overlap.
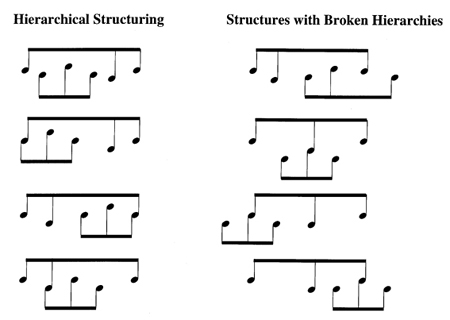
Example 7 contains several abstract illustrations of interpolation and interpolation with imbrication. As indicated in the example, not all of the forms attain equal status within their groupings. Like three-note gestures in tonal music, such as passing motions and neighbor motions, the first and last notes of shape/interval motives often acquire more prominence in the texture than those that occur in the middle of the motive, although other aspects of the music, such as rhythm and registral placement, may influence this perception.10 To the extent that beginning and ending pitches take precedence in a motive, interpolated motives whose strongest pitches dominate their time-spans may be preferred over interpolations in which the temporal hierarchy is broken. The forms in the left-hand column of Ex. 7 meet this criteria whereas those in the right-hand column do not. The forms on the left either interpolate the entire motive or imbricate motivic pitches that are hierarchically emphasized, that is, first or last, in both motives. In the interpolation that appears at the top of the right-hand column, however, the hierarchical time-span of the motive that occurs first is broken by the entrance of a second motive on the same level. In each of the other examples in the right-hand column, the weak middle member of the interpolated motive overlaps with a pitch on a higher level and, thus, breaks across hierarchical boundaries. Imbrications and interpolations might be difficult to recognize were it not for the fact that the passages in which these operations typically occur contain few non-motivic tones. Most, if not all, of the notes in the melodies in Ex. 8, for instance, are saturated by a single shape/interval motive and its imbricated or interpolated variations.
Example 7. Temporal Hierarchies.
Example 8a. Pitch and Interval Imbrication.
Bartók, Mikrokosmos, No. 101, Diminished Fifth, mm. 12-18.
Example 8b. Interpolation.
Stravinsky, Rite of Spring, Tableau 1.

Example 8c. Interpolation with Imbrication.
Schoenberg, Pierrot Lunaire, Nacht, mm. 8-9.

Part of what gives direction to a composition is the way in which germinal motives evolve through gradual changes to their basic structure. Where shape/interval motives are concerned, melodic material may be derived not only through the chaining of ordered motives, but also through the gradual degeneration of the shapes and intervals themselves. Such transformations provide a link between motives that differ with regard to their specific ordered pitch intervallic content, but conform to a similar pattern. Let us assume, for example, that we have a three-note motive with a total ordered intervallic content consisting of an ascending major second (+2), an ascending minor third (+3), and a descending perfect fourth (-5).11 We can lay this motive out in such a manner that the perfect fourth occurs between the first and last pitches, as illustrated in Ex. 9a (7 - 12 = -5). The inversion, which maintains this order, appears in Ex. 9c. By retaining the intervallic sequence 2/3, yet selectively changing the direction of the intervals, we arrive at the secondary motives shown in Examples 9b and 9d. These motives maintain the succession of intervals found in the original and inversion, but the direction of the second interval is inverted. This has the affect of altering the pitch content of the motive and, consequently, its set class along with its total intervallic content (5 is replaced by 1 in both shape-altered motives).12 We will refer to motives altered in this way as shape hybrids because they combine ordered and unordered operations.
Example 9.
Intervallic alterations to a shape/interval motive may take one of two forms: the alteration of an interval's size or the reordering of the temporal sequence of the intervals in the motive. Generally speaking, small expansions or contractions in the size of an interval—those consisting of a semitone, for instance—are probably easier to recognize than larger alterations. Under certain conditions, however, strong connections can be forged between motives with larger expansions and contractions. Consider, for instance, the fugal entries in Bartók's Concerto for Orchestra, mvt. 1 shown in Ex. 10a. Here the ascending +5 at the beginning of the subject is replaced by an ascending +7 in the answer. Except for the initial interval, the intervallic content of the two melodies, as well as their contour and rhythm, is identical. The intervallic expansion in the answer, moreover, duplicates the pitch class of the subject. Example 10b contains an excerpt in which the contour of the source motive remains the same in the derivative motive while its intervals contract by an octave. In this case, the large leaps in the source motive merely exaggerate the motive's basic shape, which is determined by the relative height of its pitches.
Example 10a. Bartók, Concerto for Orchestra, mvt. 1, mm. 328-38.

Example 10b. Copland, Piano Variations.

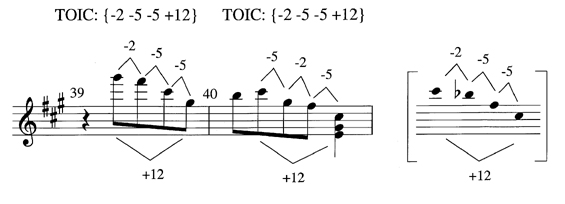
The back-to-back motives in Ex. 11, which are repeated several times over the course of the movement, share the same shapes and intervals, but present these in a different temporal ordering. Unordering the intervals of a motive has the effect of changing the motive's pitch content while replicating its ordered pitch intervals. The bracketed motive to the right of the excerpt contains the same succession of intervals as the motive in m. 39, but begins on c''' like the motive in m. 40. The pitches of the two motives differ, but the total ordered intervallic content, in this case <-2, -5, -5, +12>, remains the same because the pitch intervals themselves are ordered and, thus, commute.
Example 11. Ravel, Valses nobles et sentimentales, mvt. 7, Moin vif.
Intervallic degeneration can be a convenient catch-all in passages where pitches do not group into a prevalent intervallic contour. This may lead to excessive application of intervallic expansion and contraction to account for motivic organization in difficult music. Consider the motivic analysis of Hindemith's Piano Sonata No. 2, mvt. 1 shown in Ex. 12a. Each of the bracketed motives in this example outlines a similar contour. Metric accents and intervals, on the other hand, vary from one motive to the next. The opening motive, for example, ends precariously on a passing  ', which arrives in the middle of a weak measure of the three-measure hypermeter.13 It is easier to hear the opening gesture as an ascent to D that embeds two three-note motives consisting of a major second and a minor third as illustrated in Ex. 12b. The
', which arrives in the middle of a weak measure of the three-measure hypermeter.13 It is easier to hear the opening gesture as an ascent to D that embeds two three-note motives consisting of a major second and a minor third as illustrated in Ex. 12b. The 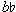 '-a' motion (m. 2) in this hearing, relaxes the upward momentum of the first measure, allowing for a brief catch of breath before the final push to D, which is emphasized because it arrives on the final beat of the first hyper-measure, m. 3 in the notated meter. This <+2 +3> ascending motive is even more pervasive than the four-note shape motive outlined in Ex. 12a. Indeed, the motives in Ex. 12b not only conform better to the three-measure hypermeter, but also help to highlight the large-scale ascent that takes place over the first twenty-nine measures of the piece, shifting d'' up an octave to d''' in m. 29. The analysis of the melody in Ex. 12c employs intervallic expansion and contraction in a more systematic way than the analysis of the melody in Ex. 12a. This excerpt contains a repeated intervallic contour in which the second interval expands on each repetition. Despite the occurrence of intervallic degeneration, the motives in the excerpt maintain close connections not only because they contain many of the same intervals, but also because they receive similar rhythmic treatment and follow a similar contour.
'-a' motion (m. 2) in this hearing, relaxes the upward momentum of the first measure, allowing for a brief catch of breath before the final push to D, which is emphasized because it arrives on the final beat of the first hyper-measure, m. 3 in the notated meter. This <+2 +3> ascending motive is even more pervasive than the four-note shape motive outlined in Ex. 12a. Indeed, the motives in Ex. 12b not only conform better to the three-measure hypermeter, but also help to highlight the large-scale ascent that takes place over the first twenty-nine measures of the piece, shifting d'' up an octave to d''' in m. 29. The analysis of the melody in Ex. 12c employs intervallic expansion and contraction in a more systematic way than the analysis of the melody in Ex. 12a. This excerpt contains a repeated intervallic contour in which the second interval expands on each repetition. Despite the occurrence of intervallic degeneration, the motives in the excerpt maintain close connections not only because they contain many of the same intervals, but also because they receive similar rhythmic treatment and follow a similar contour.
Example 12.
Hindemith, Piano Sonata No. 2, mvt. 1.


Ives, Incantation.

Like intervallic degeneration, shape hybridization can be over-used. Example 13, on the other hand, shows two instances in which shape hybridization provides a musically viable explanation for the events in each melody. In these excerpts, shape hybrids stand out because the melodies are saturated by two or three intervals and contain similar rhythmic patterns. Shape hybrids can be identified most easily on the basis of their unordered pitch-intervallic succession and shape relation to the original shape/interval motive.
Example 13.
Bartók, String Quartet No. 6, mvt. 1, mm. 73-76.

Schoenberg, Five Pieces for Orchestra, Op. 16, mvt. 1, mm. 63-68.

The foregoing presents a number of analytical tools in which shape/interval motives, along with their systematic relations and transformations, play a significant role. Many of the processes we have been describing, such as imbrication and interpolation, are familiar concepts. We have formalized these and other transformations into an analytical system aimed at enhancing our observations of twentieth-century music in order to create a model that can facilitate the specific analytical tasks necessary for the effective aural/analytical interpretation of twentieth-century musical masterworks representative of a variety of compositional styles. In the following section, we will develop this approach further by demonstrating how shape/interval motives and their transformations can serve as the basis for the aural analysis of melodies in broader contexts.
Analytical Applications
Most of the examples presented thus far contain motives that reside near the surface of the music. Clear-cut examples of this kind can be extremely useful for practicing aural skills. The analytical study of shape/interval motives, however, need not end here. Shape/interval motives may also be used to account for large-scale organization within complete pieces and movements. Debussy's String Quartet provides one outstanding example. The first movement of the piece begins with a descending three-note shape/interval motive, <-2 -3>, outlined by the pitches G, F, and D. This motive recurs throughout the composition, including succeeding movements, where it is subjected to intervallic as well as shape alterations.
Another example is Debussy's Prelude to the Afternoon of a Faun whose highly ornamented principal shape/interval motive only gradually becomes apparent as the piece unfolds. The first unornamented version of this motive—in this case, the inversion—occurs in mm. 15-16 and is shown in Ex. 14a.14 The motive is strongly established over the next several measures where it undergoes a series of transformations illustrated by labeled brackets in the example. As Ex. 14b indicates, the original version of this motive, while filled in chromatically, also forms the basis for the opening theme in mm. 1-2. The opening phrase, moreover, ends with a hybrid original, also bracketed in the example.
Example 14. Debussy, Prelude to the Afternoon of a Faun.

Example 15 shows how the motive, thus established, resurfaces in a number of important melodic figures over the course of the composition. The two imbricated motives shown in Ex. 15a, for instance, combine to form a new melodic idea that begins in m. 37. Measure 55 ushers in a change of tempo along with the lyric melody shown in Ex. 15b. This melody presents the motive in its most undecorated form since the beginning of the piece. In mm. 86-90, the opening theme is adjusted to fit the key of 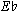 major, which allows the motive to emerge more forcefully than in its first presentation. Here, the notes of the motive, bracketed in Ex. 15c, are accented metrically and agogically. As Ex. 15d illustrates, the motive is heard for a final time in the harp part as the piece nears its end in m. 106. Just as in the opening theme, the descending major second in this case is filled in chromatically.
major, which allows the motive to emerge more forcefully than in its first presentation. Here, the notes of the motive, bracketed in Ex. 15c, are accented metrically and agogically. As Ex. 15d illustrates, the motive is heard for a final time in the harp part as the piece nears its end in m. 106. Just as in the opening theme, the descending major second in this case is filled in chromatically.
Example 15.

While some compositions center around a single shape/interval motive and its transformations, others may incorporate an interplay between several motives. The second movement from Hindemith's String Quartet No. 5 in 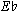 provides a case in point. The movement begins with a three-note motive consisting of a descent of one semitone followed by an ascent of three semitones, designated O1 in Ex. 16a. This motive and its permutations remain prominent throughout the first twenty measures of the piece where they constitute the basis for the opening theme. The subordinate theme, shown in Ex. 16b, arrives in m. 27. This new theme along with its embedded <+5 -3> shape/interval motive (O2) is firmly established over the next thirteen measures. As Ex. 16c illustrates, O1 returns in m. 40, beginning a section in which both themes overlap in a manner typical of Hindemith's layered textures.
provides a case in point. The movement begins with a three-note motive consisting of a descent of one semitone followed by an ascent of three semitones, designated O1 in Ex. 16a. This motive and its permutations remain prominent throughout the first twenty measures of the piece where they constitute the basis for the opening theme. The subordinate theme, shown in Ex. 16b, arrives in m. 27. This new theme along with its embedded <+5 -3> shape/interval motive (O2) is firmly established over the next thirteen measures. As Ex. 16c illustrates, O1 returns in m. 40, beginning a section in which both themes overlap in a manner typical of Hindemith's layered textures.
Example 16. Hindemith, String Quartet No. 5 in E-flat, mvt. 2; First Theme.

Although Hindemith denotes the beginning of the development section in m. 65 with a double bar line, the motivic material itself remains unvaried until m. 82 where the principal O1 motive undergoes a series of intervallic expansions. These are denoted with V-shaped brackets in Ex. 17.
Example 17. Interval Expansion.

In this case, rhythmic similarities strengthen the aural connections between the original motive and the derivative motives in the development because both incorporate a dotted eighth/sixteenth-note grouping. The opening thematic flourish, expressed by the tutti theme played in octaves, returns in m. 158. This version of the theme, however, does not begin on E as the initial presentation of the theme does, but rather is transposed to begin on 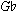 . As Ex. 18 illustrates, the piece finally reaches closure after wending its way back to
. As Ex. 18 illustrates, the piece finally reaches closure after wending its way back to 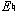 before descending to
before descending to 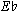 in m. 178.
in m. 178.
Example 18.

While the movement ends on an 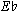 major triad, it does not follow a traditional key scheme, nor are keys themselves established through traditional functional protocol. Rather, centric pitches emerge in this music due to their prominence in melodic gestures, those identified as O1 and O2 in the analysis. The principal centric pitches in the piece, and the gestures that embed them, are shown in Ex. 19a. The motives in mm. 65 and 158 occur at the beginning of sections delineated by double bar lines. The other two motives, i.e., those occurring in mm. 1 and 26, mark the beginnings of the two principal themes. Taken together, and reduced to a single octave, the initial pitches of these motives, along with the final melodic pitch of the movement, form two imbricated versions of the two principal shape/interval motives in the piece as illustrated in Ex. 19b. Thus, the formal organization of the piece, like its individual sections, can be explained in terms of motivic intervals and shapes rather than key relations and harmonic function.
major triad, it does not follow a traditional key scheme, nor are keys themselves established through traditional functional protocol. Rather, centric pitches emerge in this music due to their prominence in melodic gestures, those identified as O1 and O2 in the analysis. The principal centric pitches in the piece, and the gestures that embed them, are shown in Ex. 19a. The motives in mm. 65 and 158 occur at the beginning of sections delineated by double bar lines. The other two motives, i.e., those occurring in mm. 1 and 26, mark the beginnings of the two principal themes. Taken together, and reduced to a single octave, the initial pitches of these motives, along with the final melodic pitch of the movement, form two imbricated versions of the two principal shape/interval motives in the piece as illustrated in Ex. 19b. Thus, the formal organization of the piece, like its individual sections, can be explained in terms of motivic intervals and shapes rather than key relations and harmonic function.
Example 19.

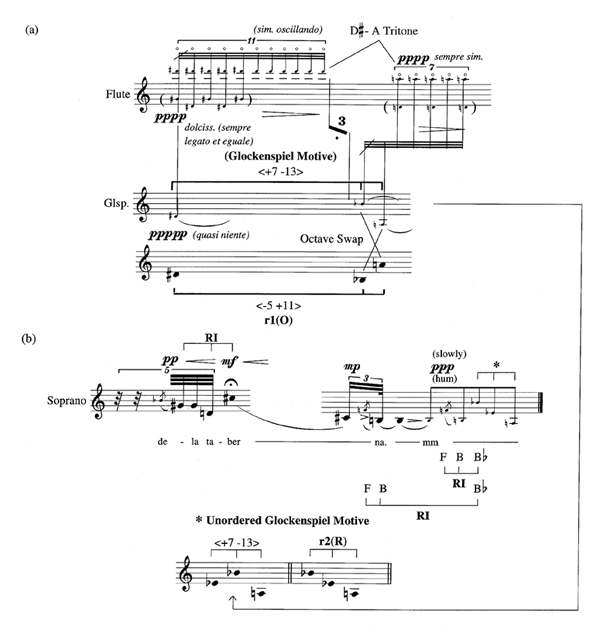
As the discussion of Examples 10 and 11 suggests, octave shifts and unordering may also come into play where shape/interval motives are concerned. George Crumb's music is especially instructive with regard to these techniques because Crumb typically reorders shapes and intervals in systematic ways that can be easily detected through aural analysis alone. The second movement of Crumb's Madrigals, Book 2, La muerte entra y sale de la taberna ("Death Goes In and Out of the Tavern"), for instance, begins with a three-note shape/interval motive that is altered through rotation and octave displacement over the course of the somber and somewhat sinister composition.15 Like the motive in Debussy's Prelude to the Afternoon of a Faun, this motive comes into sharper focus as the piece unfolds; that is, its first occurrence, reproduced in Ex. 20a, includes a grace note (circled in the example), whose elaborative role becomes clear only upon successive hearings. The grace notes in the soprano and timpani motives shown in Ex. 20b, for example, embellish the final pitch instead of the first. Despite these elaborative contrasts, the intervals of the three-note motive remain prominent in the timpani and vocal parts during the early stages of the composition.
Example 20. Crumb, Madrigals, Book 2, II, La muerta entra y sale de la taberna.

The glockenspiel part, on the other hand, introduces an unordered variation of the motive, <+7 -13>, that plays an increasingly important role as the piece continues. This motive, bracketed in Ex. 21a, is linked to the first motive by means of rotation in conjunction with octave displacement; specifically, the last two pitches of the rotated and transposed original motive, notated on the lower staff, swap octaves, a move that changes the intervallic content of the motive, but leaves its pitch-class content intact. In the rotation, the tritone, prominent in the opening motive, is obscured because it occurs between the first and last pitches of the motive instead of between consecutive pitches as in the original version. At the same time, the perfect fourth, formed by the outer pitches of the original motive, is brought into greater prominence because its pitches move into adjacent positions in the rotation. The flute harmonics, which accompany the glockenspiel, on the other hand, help the listener forge a connection between the two motives by articulating the separated pitches of the 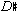 -A tritone an octave higher. As Ex. 21b illustrates, the piece ends with a rotation of the untransposed glockenspiel motive (bracketed and marked by an asterisk in the example), where it occurs in the soprano part alongside two retrograde versions of the original <+11 -6> shape/interval motive.
-A tritone an octave higher. As Ex. 21b illustrates, the piece ends with a rotation of the untransposed glockenspiel motive (bracketed and marked by an asterisk in the example), where it occurs in the soprano part alongside two retrograde versions of the original <+11 -6> shape/interval motive.
Example 21.
Closing Remarks
As the above analyses indicate, shape/interval motives constitute only a part of a composition's total context. It is when we take into consideration many aspects of a composition, i.e., its large-scale structure, its texture, its goal-directed motions, its pitch collections, its moments of intensification and inactivity, that motivic analysis can lead to the most satisfying results. The intellectual motivations of the analyst, moreover, are an integral part of the analytical process and, in our view, cannot be separated from it. Music is a complex phenomenon, one that embodies many musical properties including harmony, rhythm, meter, and form. Thus, motivic analysis will be most effective when understood as part of a complete musical process. Our analytical system offers no inherent musical meaning in itself. Instead, we posit it as a tool that can empower individuals to attain meaningful musical/analytical self-derived experiences based on their own intellectual explorations, ones stemming from their basic working out of the system. It is one's individual interpretive use of the system, and not the system itself, then, that enables individuals to arrive at their most worthwhile observations. Approached in this way, motivic analysis centering around intervallic contours and their ordered transformations can be a powerful tool for the aural analysis of twentieth-century music inclusive of a wide variety of styles and genres.
References
Austin, William W. "Toward an Analytical Appreciation." In Debussy: Prelude to "The Afternoon of a Faun." Ed. William W. Austin, 71-96. New York: W.W. Norton, 1970.
Benjamin, William E. "Ideas of Order in Motive Music." Music Theory Spectrum 1 (1979): 23-34.
Bernard, Jonathan W. The Music of Edgard Varèse. New Haven: Yale University Press, 1987.
Browne, Richmond. "The Structure of Atonal Music by Allen Forte" (Review). Journal of Music Theory 18/2 (1974): 390-415.
DeWitt, Lucinda A. and Crowder, Robert J. "Recognition of Novel Melodies After Brief Delays." Music Perception 3/3 (1986): 259-74.
Dowling, William J. and Fujitani, Diane S. "Contour, Interval, and Pitch Recognition in Memory for Melodies." Journal of the Acoustical Society of America 69/2 (1971): 524-31.
Edworthy, Judy. "Interval and Contour in Melody Processing." Music Perception 2/3 (1985): 375-88.
Forte, Allen. The Structure of Atonal Music. New Haven: Yale University Press, 1973.
Friedmann, Michael L. Ear Training for Twentieth-Century Music. New Haven: Yale University Press, 1990.
. "A Methodology for the Discussion of Contour: Its Application to Schoenberg's Music." Journal of Music Theory 29/2 (1985): 223-48.
Gilbert, Steven E. The Trichord: An Analytical Outlook for Twentieth-Century Music. PhD diss., Yale University, 1970.
Gingerich, Lora L. "A Technique for Melodic Motivic Analysis in the Music of Charles Ives." Music Theory Spectrum 8 (1986): 75-93.
Marvin, Elizabeth West and LaPrade, Paul A. "Relating Musical Contours: Extensions of a Theory for Contour." Journal of Music Theory 31/2 (1987): 225-67.
Morris, Robert D. "Recommendations for Atonal Music Pedagogy in General; Recognizing and Hearing Set-Classes in Particular." Journal of Music Theory Pedagogy 8 (1994): 75-134.
. Composition with Pitch-Classes: A Theory of Compositional Design. New Haven: Yale University Press, 1987.
Pearsall, Edward R. Trees and Schemas: A Cognitive Approach to Tonal Music. PhD diss., University of Wisconsin, 1993.
. "Multiple Hierarchies: Another Perspective on Prolongation." Indiana Theory Review 17/1 (1996): 37-66.
Pople, Anthony. "Skryabin's Prelude, Op. 67, No. 1: Sets and Structure." Music Analysis 2/2 (1983): 151-73.
Rahn, John. Basic Atonal Theory. New York: Schirmer Books, 1980.
Roeder, John. "A Geometric Representation of Pitch-Class Series." Perspectives of New Music 25/1-2 (1987): 362-409.
Winold, Allen. "Rhythm in 20th-Century Music." In Aspects of 20th-Century Music. Ed. Gary E. Wittlich, 209-69. Englewood Cliffs, NJ: Prentice-Hall, 1975.
1Benjamin, "Ideas of Order." Bernard, The Music of Edgard Varèse. Browne, "The Structure of Atonal Music by Allen Forte" (Review). William E. Benjamin puts this idea in the strongest possible terms when he states that "in my view, misuse of the new technology for dealing with motivic music has taken the form of attempts to apply all of the relations defined in the theory of unordered pitch-class sets to each an [sic] every analytical context." See Benjamin, "Ideas of Order," 23. Benjamin advocates featuring subsets [of the twelve-tone aggregate] based on "the way a particular set is ordered" (Ibid., 26).
2Robert Morris also emphasizes small sets in his set-theory approach to teaching twentieth-century analysis. See Morris, "Recommendations for Atonal Music Pedagogy."
3Michael L. Friedmann's well-known aural skills method for twentieth-century music provides a thorough grounding in aural analysis based on a set theory approach. See Friedmann, Ear Training.
4DeWitt and Crowder, "Recognition of Novel Melodies," 273. Judy Edworthy comes to a similar conclusion, noting that "when a melody is heard once and is then transposed, contour information is immediately accessible. In contrast, interval information is shown to be imprecise immediately after transposition takes place, and the ability of a listener to detect a change in interval size is shown to actually improve as a melody progresses." See Edworthy, "Interval and Contour," 387. Edworthy also observes that "although immediately precise, contour information is easily lost whereas interval information, once obtained, is more resistant to forgetting" (Ibid.). For discussions of other relations in contour space see: Michael L. Friedmann, "A Methodology for the Discussion of Contour;" Robert Morris, Composition with Pitch-Classes, 27-29; and Elizabeth West Marvin and Paul A. Laprade, "Relating Musical Contours."
5This procedure is similar to that used by John Rahn to designate ordered pitch intervals, except that Rahn omits plus signs for ascending intervals. See Rahn, Basic Atonal Theory, 21 and 41. We include plus signs here in order to emphasize the dual nature of shape/interval motives; every motion is defined both by its shape, + or -, and its interval size measured in semitones. Pitches in this model merely outline shapes and intervals and, hence, are not included in the definition.
6The fact that shape/interval motives can be accessed easily through shape and register apart from their specific intervallic content suggests that they may be more aurally accessible as well.
7For consistency we will identify transpositions in pitch-space rather than pitch-class space. Subscripts without a sign denote an upward transposition by the designated number of semitones in pitch-space while subscripts preceded by a negative sign denote a downward transposition.
8Stephen E. Gilbert (1970) and Allen Forte (1973) use the term imbrication to describe overlapping pitches in trichords and pitch-class sets. See Gilbert, The Trichord, and Forte, The Structure of Atonal Music, 83. Anthony Pople argues against using imbrication as an analytical tool because imbrication "generates" pitch succession and, as such, conflicts with analytical processes, which for Pople must always be reductive. See Pople, "Skryabin's Prelude," 151. In contrast, the analytical method we are advocating takes a top-down approach. Hence, we agree with Robert Morris who states that "the compositional flow can be modeled by a move from the basic idea to one of the potential realizations—a one-to-many relation." See Morris, "Recommendations for Atonal Music Pedagogy," 71. Under these conditions, analysis imitates the act of composition in that it reconstructs a composition according to an underlying organizational premise. Lora Gingerich formalizes the notion of interpolation in terms of what she calls the "INSERT" function, although Gingerich focuses on non-motivic interpolations (insertions) rather than motivic interpolations. See Gingerich, "A Technique for Melodic Motivic Analysis," 77.
9More than one interval may be imbricated if an interval along with its shape is repeated in a motive. Consider, for instance, a motive with the succession <-1 +4 +4>. The retrograde inversion of this motive is <+4 +4 -1>. In this case, the three pitches outlining the interval contour +4/+4 can be imbricated, creating two overlapping intervals.
10I have explored this property of three-note gestures more thoroughly in my dissertation and a subsequent article on the same subject. See Pearsall, Trees and Schema, and "Multiple Hierarchies."
11The total ordered interval content of a shape/interval motive is obtained by tallying up the ordered intervals of the motive interpreted as a pitch-cycle in which the last pitch wraps around to connect to the first. John Roeder has developed a similar model for determining the total intervallic content of trichords in pc-space. See Roeder, "A Geometric Representation," 364.
12The motive in Ex. 9a belongs to Forte's set-class 3-7 while the motive in Ex. 9b belongs to set-class 3-2. Three-note shape hybrids produce the same results as Jonathan W. Bernard's infoldings and unfoldings in which intervals invert around one of the pitches of a trichord. See Bernard, The Music of Edgard Varèse, 74-75.
13For a more complete description of the hypermetrical organization of Hindemith's Piano Sonata No. 2, see Allen Winold, "Rhythm in 20th-Century Music," 212-16.
14We consider the heavily ornamented version of the motive in m. 1 to be the original motive in this case because it occurs first in the composition. Because it is masked by the intense chromaticism of the opening gesture, this motive may only become apparent in retrospect. William W. Austin also highlights the notes of this motive in his "hypothetical simplification" of the opening flute passage. See Austin, "Toward an Analytical Appreciation," 76.
15Along with the tempo indication, Crumb specifies that the performance should produce an "eerie, spectral" effect.


