Since David Lewin summarized his ideas about "transformational theory" in Generalized Musical Intervals and Transformations,1 it has become an increasingly fruitful approach to thinking about music. In particular, one group of transformations has proven useful in approaching nineteenth-century chromaticism. These are the ones derived from some relations explored by Hugo Riemann and thus called "neo-Riemannian."2 However, when discussing transformational theory with musicians in general and non-theorists in particular, I have consistently run up against three types of resistance. First, there is an entirely understandable suspicion of yet another "theory." Second is a difficulty grasping what is "transformational," and therefore new and necessary, about transformational theory. Third, the common resistance to "math" in analysis is exacerbated by the language of mathematical group theory in which neo-Riemannian ideas are frequently expressed.
I would like to present analyses of two Schubert songs, "Der Jüngling und der Tod" (D. 545, March 1817) and "Trost" (D. 523, January 1817), that I have found helpful in addressing and overcoming these resistances. They have two additional features that recommend them. First, they are both analyses of fairly short songs, so their structures are easy to grasp. Second, the structures created by the neo-Riemannian relations in these two songs are different from, yet complementary to, those in the only other full-piece analysis published, Richard Cohn's analysis of Schubert's B-flat Sonata.3
Transformational Theory
Of the three types of resistance I mentioned, the use of mathematical language is the easiest to address, simply by avoiding such language, or at least minimizing it. The other two, the suspicion of yet another theory and the difficulty grasping what is "transformational" about it, are closely related and can be initially addressed by a brief introduction to transformational theory in general. The question "why do we need yet another theory," when asked in good faith, can be answered by demonstrating that there are musically significant or interesting phenomena that are not explained well by existing theories.
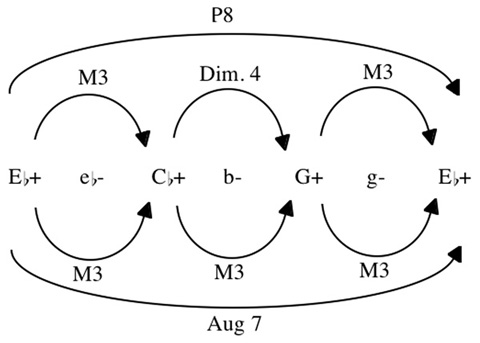
For transformational theory, the standard example of such a phenomenon is an equal interval cycle, the motion enharmonically—usually by major or minor third—through a complete octave.4 Example 1a shows the score of the complete major third cycle from the coda of Schubert's E-flat Trio, D. 929, with the triads of that cycle labeled.5
Example 1a. Complete major third cycle from Schubert,
Major Trio, D. 929.

Our existing theories, and even our notation, are unable to accurately reflect our experience of the passage. Since it is a sequence, we hear a passage of music that leads smoothly to its transposed repetition. We then hear it lead in the same way to yet another repetition, and again in the same way to return to the original key. We have no language within conventional analysis with which to describe this dual experience that reflects both that we move by the same type of root motion between legs of the sequence, and that we return to our starting point. If we move by major third three times, conventional theory insists we have in fact moved a total of an augmented seventh (the bottom arrows on Example 1b). That is, from 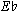 major to
major to 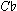 major is a major third. If the next step is in fact another major third it should take us to
major is a major third. If the next step is in fact another major third it should take us to 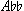 major. Another major third would then take us to
major. Another major third would then take us to 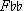 major, an augmented seventh below the initial
major, an augmented seventh below the initial 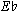 . If, however, we insist we have returned to the same key (i.e., moved an octave), then one of the "major thirds" must have been a diminished fourth (the top arrows on Example 1b). We must resort to invoking "enharmonicism" and vaguely waving our hands. The problem is of course so deeply entwined in our theory (i.e., the language we use to describe music) that it is embedded in the notation: Schubert has to include an enharmonic shift, the diminished second between
. If, however, we insist we have returned to the same key (i.e., moved an octave), then one of the "major thirds" must have been a diminished fourth (the top arrows on Example 1b). We must resort to invoking "enharmonicism" and vaguely waving our hands. The problem is of course so deeply entwined in our theory (i.e., the language we use to describe music) that it is embedded in the notation: Schubert has to include an enharmonic shift, the diminished second between 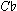 major and B minor.
major and B minor.
Example 1b. Conflicts with traditional labeling of triads.
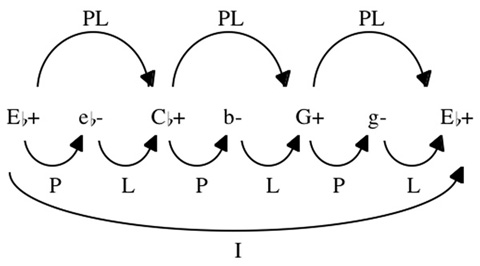
Example 1c. Consistent labeling of transformations.
The problem arises because our theories label "objects" (i.e., chords, roots, intervals, etc.) but what we are hearing are relations and transformations between those objects. The essence of what makes transformational theory "transformational" (the second point of resistance) is that it tries to focus attention on the relations, not on the objects. David Lewin illustrates this with a picture, Example 2.6
Example 2. The basic transformational situation, following GMIT, Figure 0.1.
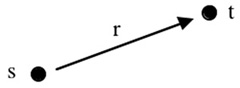
Our traditional approaches start with the objects "s" and "t" and treat the relation between them (the arrow "r") as secondary; the relation is determined by or derived from the objects. Transformational theory starts with the arrow "r" and treats the objects "s" and "t" as secondary; the objects are derived from the transformation. For instance, given the transformation and a starting object, the resulting object is determined (i.e., there is only one possibility). Similarly, given the transformation and the resulting object, the starting object is determined. Elsewhere Lewin has tried to describe the "transformational attitude" as the point of view from which "the interval labels the transformation itself; it is a name for 'a way of moving' (from anywhere to somewhere else), rather than a relation between fixed points in musical space."7
Transformational theory can clearly be a huge subject, and one of the virtues of Lewin's explorations of it is the wide variety of different types of transformations he explores.8 Essentially, each piece can suggest those transformations that are particularly pertinent to itself, and no two pieces need to explore the same transformations. However, one group of transformations has proven repeatedly useful in a variety of nineteenth-century harmonic contexts, including the equal interval cycle. These are the transformations among triads derived from the work of Hugo Riemann, forming the basis of the subset of transformational theory know as "neo-Riemannian Theory."9 For most purposes we need only three of these relations, known by the letters L, R, and P.
The easiest way to understand these relations is that they are the three ways to relate two consonant triads (i.e., major or minor) that share two pitch classes. P stands for "Parallel" and relates two triads that could be tonics of parallel-related keys. Thus, P transforms a C major triad into a C minor triad, and also transforms a C minor triad into a C major triad. The triads C major and C minor share the two pitch classes C and G. Similarly, R stands for "Relative" and transforms a C major triad into an A minor triad, and an A minor triad into a C major triad. The triads C major and A minor share the pitch classes C and E. L stands for "Leittonwechsel" which means "leading tone exchange."10 It is the third way of relating two triads that share two pitches. L relates a C major triad to an E minor triad, and an E minor triad to a C major triad. The triads C major and E minor share the pitch classes E and G.
It is worth stressing that although we are accustomed to the parallel and relative relations between keys, the transformations P and R (and also L) are defined on triads, not keys. Since we will therefore be talking a lot more about triads than keys, I will continue to indicate keys conventionally by their letter name and "major" or "minor." I will indicate triads with the following shorthand: a capital letter followed by a "+" will indicate a major triad (e.g. C+ for a C major triad), and a lower case letter followed by a "-" will indicate a minor triad (e.g. a- for an A minor triad).
These transformations allow us to capture our experience of the equal interval cycle in Example 1 as a sequence, in a way that traditional analysis does not. As the arrows on Example 1c show, between legs of the sequence we hear an L transformation, as a minor triad is transformed into the major triad with root a major third below (like 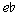 - to
- to 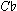 +). Within each leg of the sequence we hear a P transformation, as a major triad gives way to the minor triad on the same root. Because we are labeling the transformations and not the objects transformed we no longer have to invoke enharmonicism. Moreover, because we are labeling transformations, we can label the relations of the legs of the sequence as all the same, "PL." This labeling reflects our threefold experience of this passage more accurately than conventional analysis. Within each leg of the sequence we hear the same process, a P transformation; between the legs we hear the same process, a PL transformation; and at the end we return to where we started, that is, the cumulative effect of these P and L transformations is an I, or identity, transformation.
+). Within each leg of the sequence we hear a P transformation, as a major triad gives way to the minor triad on the same root. Because we are labeling the transformations and not the objects transformed we no longer have to invoke enharmonicism. Moreover, because we are labeling transformations, we can label the relations of the legs of the sequence as all the same, "PL." This labeling reflects our threefold experience of this passage more accurately than conventional analysis. Within each leg of the sequence we hear the same process, a P transformation; between the legs we hear the same process, a PL transformation; and at the end we return to where we started, that is, the cumulative effect of these P and L transformations is an I, or identity, transformation.
Maps
Before turning to the two song analyses, we need to explore the world of these neo-Riemannian transformations a little more closely. As I said above, L, R, and P can be understood as the three possible ways of relating two triads that share two pitches. Since L, R, and P give us a major third root relation, a minor third root relation, and a mode change relation, we can relate any two triads by a chain of L, R, and P relations. For instance C+ and  + could be related by the chain RPLP as follows: R takes C+ to a-; P takes a- to A+; L takes A+ to
+ could be related by the chain RPLP as follows: R takes C+ to a-; P takes a- to A+; L takes A+ to  -; and P takes
-; and P takes  - to
- to  +. The relations thus create a sense of relative distance among triads, proportionate to how many steps it would take to link them. More specifically, since L, R, and P relate triads that share two pitches, these relations encourage us to think of triads that share two pitches as "closely related." In contrast, the relationship between tonic and dominant triads, the "close relationship" in traditional tonal theory, is now a two-step relation (L takes C+ to e-, R takes e- to G+).
+. The relations thus create a sense of relative distance among triads, proportionate to how many steps it would take to link them. More specifically, since L, R, and P relate triads that share two pitches, these relations encourage us to think of triads that share two pitches as "closely related." In contrast, the relationship between tonic and dominant triads, the "close relationship" in traditional tonal theory, is now a two-step relation (L takes C+ to e-, R takes e- to G+).
Since the sense of distance created by these relations is so different from what we are accustomed to, it is useful to have a map that shows how L, R, and P relate triads. Such a map is easily drawn by starting with a triad, linking it by L, R, and P to three other triads, and then linking those in turn to others, always adopting a convention that each relation is represented by the same direction on the map. The result is shown in Example 3.11 As indicated by the legend, on this map any move in the North/South direction is a P relation, any move NE/SW is an R relation, and any move NW/SE is an L relation.
Example 3. The LRP map.
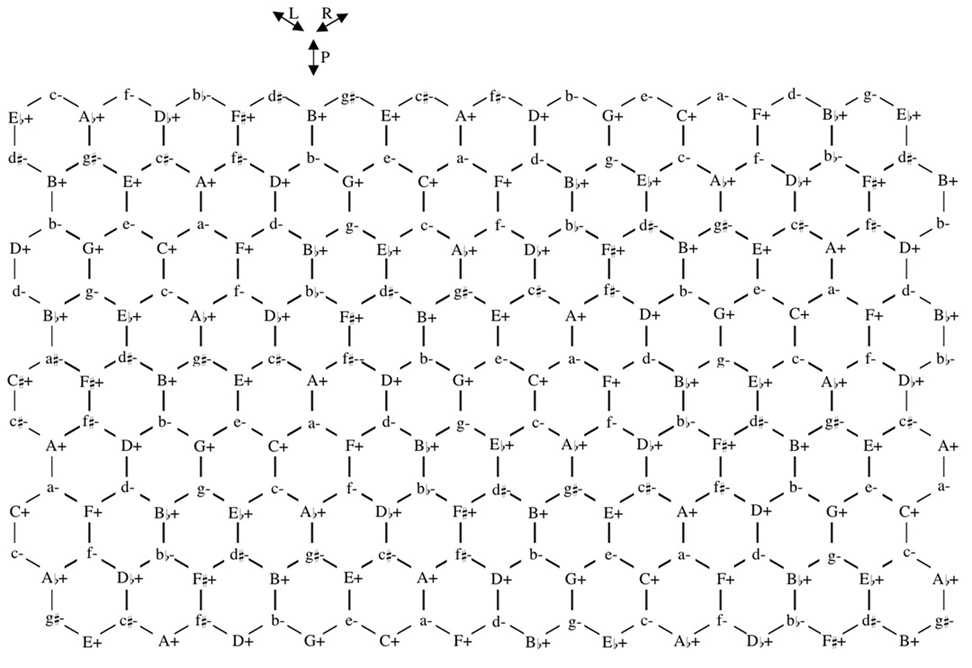
As with all such maps, how we define the relations will affect the geometry of the map. For instance, because the three relations link triads based on two shared pitches, there are no axes on this map. "R," for instance, is not simply an NE/SW axis. We can move by R NE, say from C+ to a-, but there is nothing one step further NE from a-. Further motion NE from a- would involve a leap across a hexagon, to D+. Instead, if R relates C+ to a- because they share C and E, then another move by R must move a- to the triad with which it shares C and E, and thus must return us to C+. To get anywhere on this map we must use multiple relations. That is, if R takes us from C+ to a-, we will need to use something other than R to get anywhere else. Similarly, a repeated application of L or P will return us to where we started. The technical expression for this is that these transformations are their own inverses.
However, if we conceive the relation between C+ and a- differently, we can get a different geometry, for instance, one with axes. Lewin has defined the relation between C+ and a- as "MED," a transformation through which one triad becomes interpreted as the mediant of the next triad.12 Thus C+ "becomes the mediant" of a-. This description of the transformation between C+ and a- creates an axis. A repeated application of MED does not return us to C+ but carries us further away; a- "becomes mediant of" F+, F+ "becomes mediant of" d-, etc. To get back from a- to C+ would involve a different operation, "SUBMED," read "becomes submediant of."
In describing how to derive the map in Example 3 we used the most general possible description of the relations. R for instance, directly relates the abstract entity "C+" to the abstract entity "a-." Either C+ or a- can be presented in any number of voices, and there is no implication that specific pitches in one relate to specific pitches in the other. For instance, while C+ and a- may share the pitches C and E, there is no need to suppose that the voice with C in the C+ triad must stay on C in the a- triad. R simply relates something we can call "C+" to something we can call "a-." Under these conditions we cannot distinguish between different versions of C+, so any occurrence of C+ on the map is indistinguishable from any other. In principle this means that the two dimensional map rolls in on itself to become a torus (a donut).13 That is, we could roll the top down so the C+ in the top line lines up with the C+ in the middle line, and roll the bottom up so the C+ in the bottom line lines up with the C+ in the middle, forming a cylinder. We could then roll the cylinder, and twist it, so the C+s at each end line up, and have a donut. In practice our intuitions about the relations of points on the surface of a torus are vague at best, so I find it most useful to leave the map unrolled into two dimensions and just remember that any C+ is the same C+, and the map shows only twenty-four possible positions (one for each major and minor triad). In other words, if you start at C+, and head generally NW until you reach C+ again, you have in fact returned to where you started. Similarly, if you head generally NE until you reach C+ again, you have again returned to your starting point. All three of these, and every other C+ on the map, are the same place.
The transformations L, R, and P between triads, however, are usually defined less abstractly, that is to say, with specific pitch-to-pitch relations. Perhaps the most common of these definitions are as "contextually defined inversions."14 With familiar pitch-class inversion, the pitches of C+ can be related to those of a- (an R relation) by an inversion operation, specifically I4. However, I4 is not the same as R because it also relates the pcs of F+ to those of e-, whereas R relates F+ to d-.15 In each case it relates C to E, but independent of the context (i.e., triad) in which C occurs. With a contextually defined inversion, the effect on C will be different depending on context. For instance, as a contextually defined inversion, R might be described as inverting a triad around its major third. When R relates C+ to a-, it will act as I4 and relate C to E; however, when R relates F+ to d-, it will act as I2 and relate C to D. A contextually defined operation acts on pitches only in a specific context.
This definition of R implies a specific pitch-to-pitch connection, shown in Example 4.
Example 4a. Voice leading of R as a contextually defined inversion.
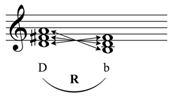
Example 4b. Voice leading of R as a contextually defined inversion, score format.
Because this voice leading is based on pitch-class inversion, a voice that starts on the root of a triad will move to the fifth of the next triad. However, because L and P are also described as contextually defined inversions, another step on the map returns that voice to the root. This reflects the fact that inversions combine to form transpositions. Because triads of the same mode are always even numbers of steps apart on the map, and thus involve an even number of inversions, a voice that starts on the root of a triad will always be on the root of any triad of the same mode, and we will again not be able to distinguish different occurrences of, say, C+.
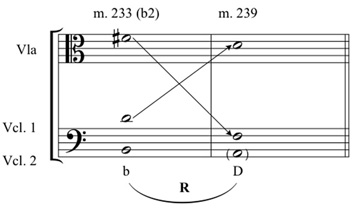
However, not all definitions work like this. Another common way of describing the relations invokes "maximally smooth voice leading,"16 as in Example 5. In these definitions the transformations are described as holding two notes constant while moving the third note by the smallest amount to create another triad. For L and P that smallest amount is a half-step. For R it is a whole-step. With this type of definition we can now distinguish different occurrences of the same triad.
Example 5a. Voice leading of R as a maximally smooth relation.
Example 5b. Voice leading of R as a maximally smooth relation, score format.
Example 6 shows the result of using this voice-leading definition, starting from C+, and alternating R and P. This produces a chain which eventually returns to C+, but with a difference.
Example 6. RP Cycle with maximally smooth voice leading.

If we had started singing the root in C+, when we arrive again at C+ we will now be singing the third, E. Although the example shows pitches in specific registers, and thus seems to show different inversions of triads, the phenomenon is really a matter of pitch class, which by its nature is register-unspecific. Conceivably there could be a fourth voice providing a root below the three pitches charted in Example 6, thus making all the triads be root position. Similarly, there could be reasons for following an octave transfer in one or more voice, again changing the actual position of the chord. What remains constant is the change of orientation of the voice to the chord: the voice that started on the root, C, has arrived on the third, E. Thus we can call these abstract arrangements "orientations" to distinguish them from more concrete "positions." Since the voices are all drifting upward (or more accurately, clockwise on a pitch-class circle), as we continue alternating R and P, when we next return to C+ we will be singing the fifth, G. We have to continue yet one more time through the cycle before we return to singing C in a C triad. We can thus distinguish three distinct C+ triads; one in which we are singing the root, one in which we are singing the third, and one in which we are singing the fifth.
Since we can now distinguish three different C+ triads, our map will have to show three forms of each major and minor triad, and thus will show seventy-two total orientations. Such a map is shown in Example 7.
Example 7. The maximally smooth LRP map.
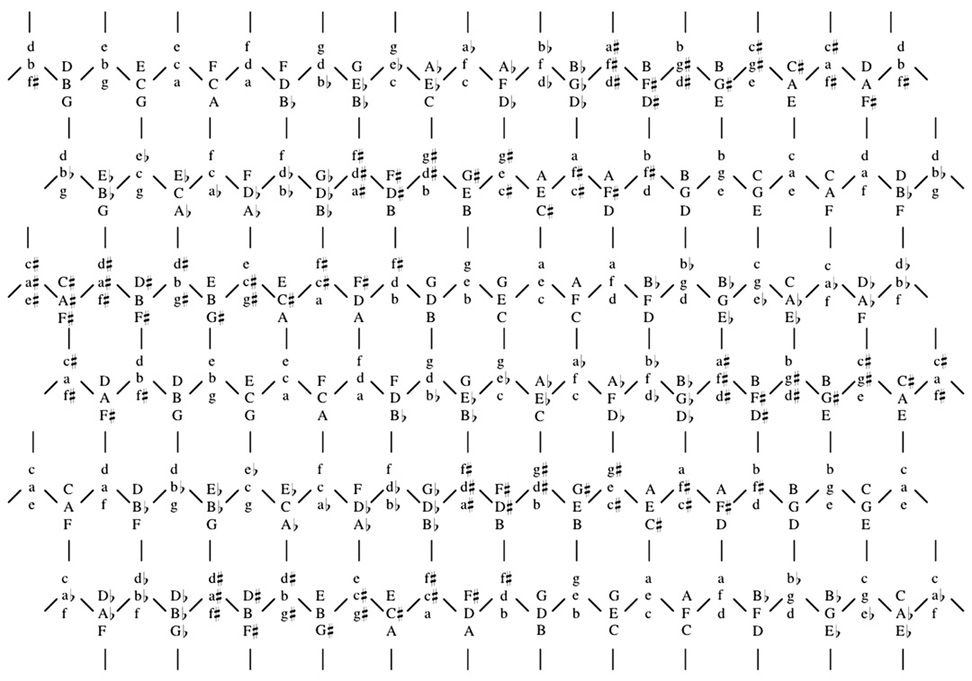
Again, it should be stressed the map shows pitch-class relations, as opposed to triad relations. The distinction is not whether a triad is in "root position" or "first inversion," but whether the voice that started on the root is again on the root or is now on another member of the triad. Thus the different descriptions of the operations produce different relations among differently defined triads. For a chord-to-chord description, or a transpositional/inversional voice-leading description, we can not distinguish different forms of the same triad, and have only twenty-four positions on the map. With a maximally smooth voice-leading description we can distinguish three orientations of each triad, so we have seventy-two places on the map.
Having introduced the neo-Riemannian transformations, we can now turn our attention to some music. Schubert wrote roughly twenty songs that start and end in different keys.17 The lack of a single governing key in such songs presents two immediate challenges. The first is simply how to make the various parts of the piece sound as though they belong together, and moreover, as though they belong in the order in which they occur. A single tonic usually creates the framework within or around which we organize our hearing of a piece. In the absence of such a tonic something else must do this job. Second, and perhaps only a special case of the first, is how to make the piece sound as though it is over when it is over, and not as though it just stopped (or with these songs, ran out of text). Again, the return to the tonic is a primary way of establishing this, and again, in the absence of a tonic, something else will have to take its place. The two songs we will look at, "Der Jüngling und der Tod" (D. 545, March 1817) and "Trost" (D. 523, January 1817), both can be considered as built around cycles created by neo-Riemannian relations to help fill in for the lack of a single tonic.18
"Der Jüngling und der Tod"
"Der Jüngling und der Tod" (Example 8) exists in two versions. In the first, for two voices, the voice singing the part of "Der Jüngling" begins the song in  minor and the voice singing the part of "Der Tod," ends the song in
minor and the voice singing the part of "Der Tod," ends the song in  major. In the second, for a single voice, the part of "Der Tod" has been transposed up a fifth to better accommodate the range of a single voice, so it ends in F major. The version for single voice is the more often recorded, but the version for two voices is more interesting. I will primarily discuss the two-voice version, but at the end I shall also look at the differences between the two.19
major. In the second, for a single voice, the part of "Der Tod" has been transposed up a fifth to better accommodate the range of a single voice, so it ends in F major. The version for single voice is the more often recorded, but the version for two voices is more interesting. I will primarily discuss the two-voice version, but at the end I shall also look at the differences between the two.19
Example 8. "Der Jüngling und der Tod" entire score.


We can understand this song as moving from  minor to
minor to  major by following an RP cycle, a chain of alternating R and P relations similar to the one discussed in Example 6. In terms of harmonic motion the piece falls into two halves. The relevant harmonies are marked on the score (Ex. 8) with asterisks, and then extracted into Example 9.
major by following an RP cycle, a chain of alternating R and P relations similar to the one discussed in Example 6. In terms of harmonic motion the piece falls into two halves. The relevant harmonies are marked on the score (Ex. 8) with asterisks, and then extracted into Example 9.
Example 9. Reduction of "Der Jüngling und der Tod."
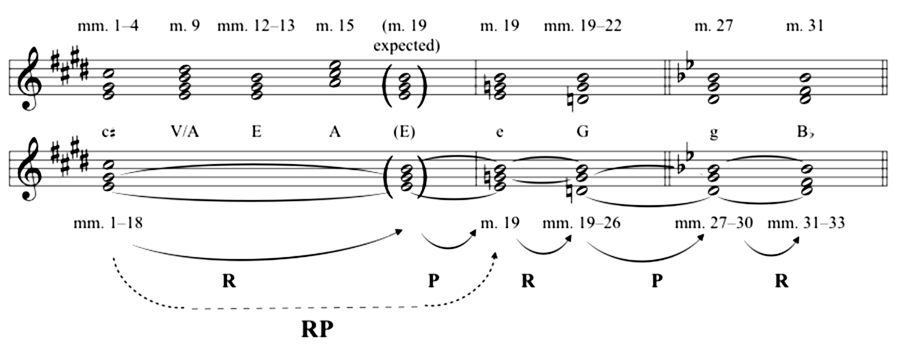
In the first half (mm. 1-18) Schubert establishes  minor (mm. 1-4) and then alternates between A+ and E+. A+, as a local tonic, is most strongly suggested by the half cadence to E7 (m. 9) and the weak internal cadence to A+ (m. 15). E+, as a local tonic, is suggested in the cadence in measures 12 and 13, and by the time we reach measure 17 we know we are headed toward a cadence to E+ (expected at m. 19). Throughout this section, recurring
minor (mm. 1-4) and then alternates between A+ and E+. A+, as a local tonic, is most strongly suggested by the half cadence to E7 (m. 9) and the weak internal cadence to A+ (m. 15). E+, as a local tonic, is suggested in the cadence in measures 12 and 13, and by the time we reach measure 17 we know we are headed toward a cadence to E+ (expected at m. 19). Throughout this section, recurring  s in the melody at the beginning of gestures (mm. 8, 10, 15) remind us that both A+ and E+ are to be understood in reference to the
s in the melody at the beginning of gestures (mm. 8, 10, 15) remind us that both A+ and E+ are to be understood in reference to the  - original tonic. This first half, then, remains entirely understandable in terms of a controlling tonic. Indeed, since E+ wins out over A+, the resulting motion from
- original tonic. This first half, then, remains entirely understandable in terms of a controlling tonic. Indeed, since E+ wins out over A+, the resulting motion from  - to E+ is the motion from i to III expected in a piece in minor.
- to E+ is the motion from i to III expected in a piece in minor.
In the second half of the piece (mm. 19-33) the motion is very different. Instead of establishing a tonic and wavering between two apparently subordinate triads, the second half moves steadily through an RP cycle. The E+ triad expected at the cadence in measure 19 is replaced with an e- triad (beat 2, a P relation), which immediately gives way to G+ (beat 4, an R relation). G+ is prolonged for several measures (mm. 20-27), confirmed by the cadence to measure 22 and the half cadence in measure 24. From this half cadence the music prepares a strong confirming cadence to G+ in measure 27. However, as with the expected E+ in measure 19, the expected G+ in measure 27 is replaced with its parallel, g-. Unlike the e- in measure 19, the g- in measure 27 is established for several measures (mm. 27-30). It gives way to  + (an R relation) with the arrival of F natural in the voice in measure 31, and the piece ends with the resolution of F7 to
+ (an R relation) with the arrival of F natural in the voice in measure 31, and the piece ends with the resolution of F7 to  + in the next measure (mm. 31-33).
+ in the next measure (mm. 31-33).
The idea of the RP cycle can help us understand why the various parts of the piece sound as though they belong together in the order in which they occur. Although the piece vacillates at first between moving by L (to A+) or by R (to E+), it finally commits to R. Indeed, it commits to R and P, since the cadence arrives on e- instead of the expected E+. From there the continued alternation of R and P gives the piece a sense of direction and helps it hold together.
The problem remains, however, of how  + can provide an end for a piece that started in
+ can provide an end for a piece that started in  -; that is, why the piece sounds as though it is over, and not as though it just stopped. Following the voice leading of these relations on the maximally-smooth map (Ex. 7) can help us answer that question. In short, the piece follows the voice leading of that map, and ends when it returns to a triad in the same orientation as it started. Usually we think of the return of pitch as the return that provides a sense of ending in music. However, since using the voice-leading map we can now distinguish among the orientations of triads, the possibility arises that the return of orientation can create that sense of ending. A return to a triad in the same orientation as the original allows each voice to return, not to its original pitch, but to its original function (root, third, fifth) within the triad.
-; that is, why the piece sounds as though it is over, and not as though it just stopped. Following the voice leading of these relations on the maximally-smooth map (Ex. 7) can help us answer that question. In short, the piece follows the voice leading of that map, and ends when it returns to a triad in the same orientation as it started. Usually we think of the return of pitch as the return that provides a sense of ending in music. However, since using the voice-leading map we can now distinguish among the orientations of triads, the possibility arises that the return of orientation can create that sense of ending. A return to a triad in the same orientation as the original allows each voice to return, not to its original pitch, but to its original function (root, third, fifth) within the triad.
In this song the voice leading of the RP cycle is made quite audible and the correct orientation of each triad is emphasized, as summarized in the reduction in Example 9 (the path can be most easily traced on Ex. 7 by starting at the  - in the top row near the right edge and moving generally SW). In addition, the fact that each voice has returned to its original triadic function is emphasized by melodic contour. At each step around the cycle, the displacement of a single voice and its motion to a new pitch is clearly articulated. Further, at each step the voice and the right hand of the piano combine to emphasize the correct orientation of the underlying triad.
- in the top row near the right edge and moving generally SW). In addition, the fact that each voice has returned to its original triadic function is emphasized by melodic contour. At each step around the cycle, the displacement of a single voice and its motion to a new pitch is clearly articulated. Further, at each step the voice and the right hand of the piano combine to emphasize the correct orientation of the underlying triad.
The piano introduction is the most tonally secure passage in the piece. It establishes four measures of uncontested  minor. More specifically, the leap to
minor. More specifically, the leap to  in measure 2 establishes
in measure 2 establishes  as the highest structural voice, while voices on
as the highest structural voice, while voices on  and E are started in measure 1. Although the
and E are started in measure 1. Although the  - triad of Example 9 does not actually occur on the surface, the first four measures elaborate
- triad of Example 9 does not actually occur on the surface, the first four measures elaborate  - in that orientation. This orientation is then confirmed by the melody, which leaps from
- in that orientation. This orientation is then confirmed by the melody, which leaps from  to
to  (mm. 4-5) and then descends to
(mm. 4-5) and then descends to  (m. 6) and finally to E (m. 7), having first leapt back to
(m. 6) and finally to E (m. 7), having first leapt back to  (m. 7) to remind us of the continuing presence of that voice.20
(m. 7) to remind us of the continuing presence of that voice.20
The first step around the RP cycle, the move by R to E+, is achieved by dropping the  to B. In the song, E+ first arrives in measure 13 as the end of the second leg of a sequence. The sequence melodically emphasizes the displacement of
to B. In the song, E+ first arrives in measure 13 as the end of the second leg of a sequence. The sequence melodically emphasizes the displacement of  (m. 10) and A (m. 11) by B (m. 12) and
(m. 10) and A (m. 11) by B (m. 12) and  (m. 13) respectively. Although the B in measure 12 is part of a B7 chord (V/E), when E+ arrives in measure 13 the correct orientation is doubled an octave lower in the piano right hand. E+ occurs again in the correct orientation and now in the correct octave in measure 18 (with E and
(m. 13) respectively. Although the B in measure 12 is part of a B7 chord (V/E), when E+ arrives in measure 13 the correct orientation is doubled an octave lower in the piano right hand. E+ occurs again in the correct orientation and now in the correct octave in measure 18 (with E and  in the piano, rh, and B in the voice), as the piece prepares for the confirming cadence expected in measure 19.
in the piano, rh, and B in the voice), as the piece prepares for the confirming cadence expected in measure 19.
The next step around the cycle is the move by P from E+ to e-, which is achieved by displacement of  by
by  . This displacement is emphasized by the substitution of the e- for the expected E+ in measure 19, juxtaposing the expected
. This displacement is emphasized by the substitution of the e- for the expected E+ in measure 19, juxtaposing the expected  with the actual
with the actual 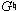 . Further, e- occurs in exactly the correct orientation and register at the confirming cadence on beat two of measure 19.
. Further, e- occurs in exactly the correct orientation and register at the confirming cadence on beat two of measure 19.
As mentioned above, e- moves immediately by R to G+, a move accomplished by the displacement of E to D. This occurs between the third and fourth beats of measure 19, and is doubled for emphasis as cover tones in the melody. The correct orientation of the G+ triad is presented in the piano right hand on beat 4. As in the E+ section, the voice returns to B (m. 22) and the piano echoes it (m. 26). The B in m. 26 reminds us of the correct orientation (original registers) of the voices, in preparation for the confirming cadence into measure 27. Again, as with the E+ section, the move by P from G+ to g- is accomplished by replacing the expected G+ in measure 27 by g-, thus explicitly displacing 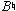 with
with  . The correct register and orientation of the triad are present in the piano right hand (with
. The correct register and orientation of the triad are present in the piano right hand (with  doubled below for emphasis).
doubled below for emphasis).
Finally, g- moves by R to  +, a move accomplished by the displacement of G with F in measures 30-31. The g- passage is largely a harmonization of a descending G minor (or
+, a move accomplished by the displacement of G with F in measures 30-31. The g- passage is largely a harmonization of a descending G minor (or  major) scale from
major) scale from  (m. 27) through A (m. 27), G, F (m. 28),
(m. 27) through A (m. 27), G, F (m. 28), 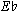 (m. 29), D (m. 30), C (m. 31), to
(m. 29), D (m. 30), C (m. 31), to  . This effectively displaces the original register down an octave for the final triad. This move was prepared by the displacement of the E+ triad at its first appearance (m. 13). The displacement of G to F thus occurs in its now correct octave, in the tenor (mm. 30-31). It is emphasized by the doubled G in measure 30 which allows us to hear the surprise F natural in the melody as an octave doubling of the F that displaces the G. The F in measure 31 arrives as part of a cadential
. This effectively displaces the original register down an octave for the final triad. This move was prepared by the displacement of the E+ triad at its first appearance (m. 13). The displacement of G to F thus occurs in its now correct octave, in the tenor (mm. 30-31). It is emphasized by the doubled G in measure 30 which allows us to hear the surprise F natural in the melody as an octave doubling of the F that displaces the G. The F in measure 31 arrives as part of a cadential 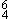 . This resolves to
. This resolves to  + in the correct orientation, which is repeated twice to bring the piece to a close. Thus the identity of the three voices is audible and distinct throughout the piece.
+ in the correct orientation, which is repeated twice to bring the piece to a close. Thus the identity of the three voices is audible and distinct throughout the piece.
In addition to emphasizing the orientations of the triads and the voice-leading displacements between them, Schubert also emphasizes the return of each voice to its original function within the triad. This return is brought out by a retrograde of melodic contour between the first and last phrases. The melody opens with a leap up from 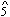 (
( ) to
) to 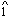 (
( ) followed by a scalar descent (mm. 4-7). The melody ends with a leap down from
) followed by a scalar descent (mm. 4-7). The melody ends with a leap down from 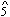 (F) to
(F) to 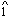 (
( ), preceded by a scalar ascent (mm. 28-33). This retrograde of melodic contour draws attention to the correspondence of initial
), preceded by a scalar ascent (mm. 28-33). This retrograde of melodic contour draws attention to the correspondence of initial  to final
to final  , and their analogous positions as roots of their respective triads. In addition, since the F in the melody is an octave doubling of the structural F below it, the retrograde emphasizes that the structural voice that started on
, and their analogous positions as roots of their respective triads. In addition, since the F in the melody is an octave doubling of the structural F below it, the retrograde emphasizes that the structural voice that started on 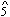 (
( ) is now again on
) is now again on 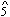 (F). Again, it is worth noting that once the final voice-leading move is completed and the
(F). Again, it is worth noting that once the final voice-leading move is completed and the  + triad established, the piece is over. The piano merely repeats the
+ triad established, the piece is over. The piano merely repeats the  + triad several times. This reinforces the argument that the return of the original orientation creates the sense of being over.
+ triad several times. This reinforces the argument that the return of the original orientation creates the sense of being over.
Two small issues remain. First, I have argued that the reason the  + can be a convincing ending for a piece that started in
+ can be a convincing ending for a piece that started in  - is that, within the context of the maximally smooth LRP map, the
- is that, within the context of the maximally smooth LRP map, the  + triad provides for a return of the original orientation of the voices. The voice that started on tonic is again on tonic, etc. However, the next step around the cycle,
+ triad provides for a return of the original orientation of the voices. The voice that started on tonic is again on tonic, etc. However, the next step around the cycle, 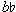 -, is also in the same orientation, and would thus seem to be able to provide the same closure. Indeed, since the
-, is also in the same orientation, and would thus seem to be able to provide the same closure. Indeed, since the  + passage sets the words of "der Tod" and there is a long tradition of setting death in minor,
+ passage sets the words of "der Tod" and there is a long tradition of setting death in minor, 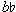 - might seem the more obvious ending. Further, since earlier expected arrivals on major triads (E+ and G+) had been elided and had slipped to the parallel minor, a listener would have been well prepared for a similar eliding of
- might seem the more obvious ending. Further, since earlier expected arrivals on major triads (E+ and G+) had been elided and had slipped to the parallel minor, a listener would have been well prepared for a similar eliding of  + and an end on
+ and an end on 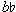 -. In the context of the RP cycle though,
-. In the context of the RP cycle though,  + remains the better stopping point. Moving on to
+ remains the better stopping point. Moving on to 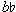 - would re-introduce the pitch
- would re-introduce the pitch 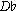 (i.e.,
(i.e.,  ), the original tonic pitch. This could overwhelm the ability of the return of the original orientation to create a sense of ending, by re-instating the expectation of the return of the original triad.
), the original tonic pitch. This could overwhelm the ability of the return of the original orientation to create a sense of ending, by re-instating the expectation of the return of the original triad.
The second issue has to do with the other version of the piece, for a single voice. My argument has been that the explicit motion through the RP cycle (or at least step-wise motion on the maximally smooth LRP map) created the context for the return of the original orientation to provide a sense of ending. In arranging the song for a single voice however, Schubert transposed the part of "Der Tod" up a fifth, thus disrupting the RP cycle (and the step-wise motion on the map). At first glance the fact that Schubert could disrupt this motion seems to suggest that it wasn't so important after all. However, a closer look at the changes he made suggests otherwise.
The most obvious change is that Schubert tacked on to the end three measures of cadential formulae (Ex. 10, mm. 32b-34b). In addition, he rewrote the figuration in the transition (mm. 24b-26b). Finally, Schubert disrupts the melodic retrograde. The melody now ends with a leap from 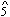 to
to 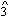 .
.
These changes can together be understood as compensation for the loss of the sense of ending that had come from the return of the original orientation. The three measures of added cadential gestures rhetorically reinforce the sense of ending that is lost by the disruption of the RP cycle. The rewritten figuration in the transition prepares the otherwise unprepared cadential gestures. Finally, the leap in the melody from 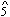 to
to 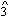 breaks the parallelism that had helped us focus on the return of each voice to its original function. Breaking this parallelism can be seen as an attempt to distract us from (or at least stop drawing our attention to) the functions of the voices, and the fact that the RP cycle that had given those functions meaning has been disrupted.
breaks the parallelism that had helped us focus on the return of each voice to its original function. Breaking this parallelism can be seen as an attempt to distract us from (or at least stop drawing our attention to) the functions of the voices, and the fact that the RP cycle that had given those functions meaning has been disrupted.
In "Der Jüngling und der Tod," then, the absence of a single controlling tonic is made up for by the use of an RP cycle. The sense that the parts of the piece belong together, and in the order in which they occur, that is usually created by understanding those parts as elaborating a tonic, can not be thus created here because of the lack of a single tonic. Instead, the purposeful motion around an RP cycle creates that sense. Similarly, the sense of completeness at the end usually created by a return to the tonic is here created by the return of each voice to its function within a triad.
Example 10. "Der Jüngling und der Tod" alternate ending.

"Trost"
The second piece we will examine, "Trost," D. 523 from January 1817, is similarly lacking a global tonic. However, unlike the through-composed "Der Jüngling und der Tod," "Trost" is set strophically, with four stanzas of text set to the same stanza of music.21 Thus in addition to the issues raised by the lack of tonic, this piece has to address the issue of how to make the same short stanza of music remain interesting as it is repeated four times. I will suggest that this song uses various characteristics of a different kind of cycle to first establish one key for the stanza, then destabilize that key, and then establish a different key.
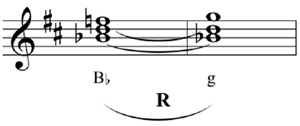
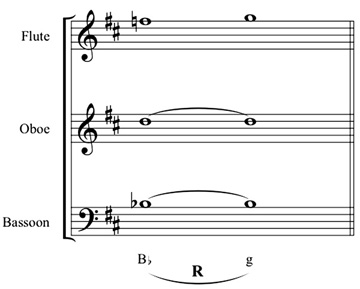
The cycle used in "Trost" can be called an LRP cycle. An LRP cycle is any of the hexagons that make up the LRP map (Ex. 3) and thus uses all three basic neo-Riemannian relations. The specific cycle used in "Trost" is shown in Example 11.
Example 11. LRP cycle of "Trost."
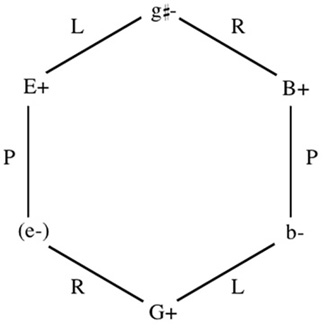
LRP cycles have two characteristics particularly worthy of note independent of any actual music. The first, which has been noted by Richard Cohn, is that they unite all six triads that share a single pitch into a single cycle.22 In the case of the cycle from "Trost," all the triads in the cycle share the pitch B. Such a cycle therefore provides the maximum variety of consonant support for a single pitch.23 The second characteristic of the cycles is that the triads in them form "opposite-mode arpeggiations;" that is, the roots of the major triads in the cycle form a minor triad (in our case, E+, G+, B+) and the roots of the minor triads form a major triad (in our case, e-, 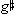 -, b-).
-, b-).
The score of "Trost," is shown as Example 12.24
Example 12. "Trost" entire score.

The song begins in  minor and ends in E major. However, at least at the beginning of the second stanza, there is a feeling of return to
minor and ends in E major. However, at least at the beginning of the second stanza, there is a feeling of return to 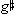 - as tonic.25 We thus never hear E major displace
- as tonic.25 We thus never hear E major displace  minor within a single stanza (as in Ex. 13a).
minor within a single stanza (as in Ex. 13a).
Example 13a. Understanding the move from
minor to E major within a single stanza.

Rather, we hear the first stanza and the beginning of the second in  minor, we hear the fourth stanza in E major, and somewhere in the second and third stanzas we switch our interpretation of the entire stanza (as in Ex. 13b).
minor, we hear the fourth stanza in E major, and somewhere in the second and third stanzas we switch our interpretation of the entire stanza (as in Ex. 13b).
Example 13b. Understanding the entire stanza first as
minor, then as E major, as it repeats.
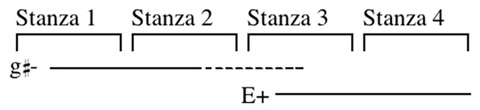
As stated above, the piece uses various characteristics of the cycle to accomplish this shift, including the common tone and the opposite-mode arpeggiation. The first time through, the more immediate characteristics of the cycle reinforce  minor. As we repeat the stanza we focus on different aspects of the cycle and thereby weaken
minor. As we repeat the stanza we focus on different aspects of the cycle and thereby weaken  minor, and, finally, by the end we focus on still other aspects and thereby establish E major.
minor, and, finally, by the end we focus on still other aspects and thereby establish E major.
Apart from aspects of the LRP cycle, there are two reasons for hearing the return of 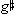 - at the beginning of the second stanza as a return to tonic. The first is simply that the stanza is so short. It has only been about 30 seconds since the beginning, so we still have the sound of
- at the beginning of the second stanza as a return to tonic. The first is simply that the stanza is so short. It has only been about 30 seconds since the beginning, so we still have the sound of  minor in our ear, and it seems too early for an initial key to be displaced. The second reason is that we have had no real reason to give up on
minor in our ear, and it seems too early for an initial key to be displaced. The second reason is that we have had no real reason to give up on  minor as global tonic; the keys we have touched on make good sense in
minor as global tonic; the keys we have touched on make good sense in  minor. As shown in Example 14 the stanza presents each of the four lines of text in a different key (or on a different triad) with two of the changes mediated by an interpolated chord. The first line is in
minor. As shown in Example 14 the stanza presents each of the four lines of text in a different key (or on a different triad) with two of the changes mediated by an interpolated chord. The first line is in  minor, the second in B major, the third in G major, and the fourth in E major. The move between B major and G major is mediated by an interpolated b-, and the move from G major to E major is mediated by an interpolated B7.
minor, the second in B major, the third in G major, and the fourth in E major. The move between B major and G major is mediated by an interpolated b-, and the move from G major to E major is mediated by an interpolated B7.
Example 14. Reduction of "Trost."

The first move, from 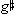 - to B+, is exactly where we might expect to move from i to III, and supports our initial impression of
- to B+, is exactly where we might expect to move from i to III, and supports our initial impression of 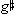 - as tonic. The move from B+ to G+ then is I to
- as tonic. The move from B+ to G+ then is I to 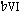 within III, and for Schubert the move to
within III, and for Schubert the move to 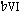 is a common place to go, especially in a second key area.26 Finally, E+ is simply
is a common place to go, especially in a second key area.26 Finally, E+ is simply 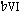 of the original
of the original 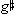 - tonic, and both the interpolated chords help us hear it as such. The b- interpolated between B+ and G+ in measure 6 presents G+ explicitly as
- tonic, and both the interpolated chords help us hear it as such. The b- interpolated between B+ and G+ in measure 6 presents G+ explicitly as 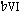 of a minor triad, preparing us to hear E+ as
of a minor triad, preparing us to hear E+ as 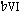 of the minor global tonic
of the minor global tonic 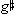 -. The B7 interpolated between G+ and E+ helps us hear E+ as
-. The B7 interpolated between G+ and E+ helps us hear E+ as 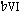 in two ways. First, by alluding to the B+ of the second line, it suggests that the B+ and G+, the previous I
in two ways. First, by alluding to the B+ of the second line, it suggests that the B+ and G+, the previous I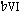 pairing, form a closed area within the global tonic. Second, by transforming III of
pairing, form a closed area within the global tonic. Second, by transforming III of 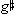 - into a secondary dominant, the B7 introduces E+ as explicitly
- into a secondary dominant, the B7 introduces E+ as explicitly 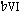 , that is, explicitly what III is V of. At the same time it suggests that E+ should be understood on the same level as the previous B+, and therefore subordinate to the global
, that is, explicitly what III is V of. At the same time it suggests that E+ should be understood on the same level as the previous B+, and therefore subordinate to the global 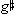 -.
-.
In addition, though, as stated above, the triads through which the piece travels form an LRP cycle (already shown in Example 11), and two aspects of that cycle help us hear the 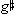 - of the second stanza as a return to tonic. The first is the simple fact that it is a cycle, and that therefore the return to
- of the second stanza as a return to tonic. The first is the simple fact that it is a cycle, and that therefore the return to 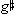 - completes it. A return to something that is also a completion of a process is a passable definition of a tonic, and thus the completion of the cycle achieved by the return of
- completes it. A return to something that is also a completion of a process is a passable definition of a tonic, and thus the completion of the cycle achieved by the return of 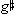 - helps us hear
- helps us hear 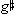 - as tonic.
- as tonic.
The other aspect of the cycle we notice in the first stanza is the common pitch shared by all the triads in the cycle, in this case B. The melody projects the voice leading shown in Example 14, and emphasizes the shared B. B first appears in measure 3, as 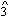 in
in  minor, and is tied into the B+ triad on the next beat. The same B returns at the end of the third line in G+, where it is again tied, this time through the interpolated B7 to E+. Thus the melody explicitly uses B as a link between two pairs of triads from the cycle, and thus supports B with four different triads (five if you include the b- in m. 6).
minor, and is tied into the B+ triad on the next beat. The same B returns at the end of the third line in G+, where it is again tied, this time through the interpolated B7 to E+. Thus the melody explicitly uses B as a link between two pairs of triads from the cycle, and thus supports B with four different triads (five if you include the b- in m. 6).
Because B is introduced as 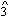 of
of  minor, and is supported throughout the stanza, a Schenkerian hearing would lead us to expect some sort of descent from B. We emphatically do not get it. When E major is reached in measure 12, B drifts chromatically up, and the melody completes a descent from
minor, and is supported throughout the stanza, a Schenkerian hearing would lead us to expect some sort of descent from B. We emphatically do not get it. When E major is reached in measure 12, B drifts chromatically up, and the melody completes a descent from  , apparently in an inner voice (m. 13). As soon as this descent has arrived at E in measure 13, the piano reasserts the B in the same register. This B now initiates a fifth descent over an E pedal, and this time, simultaneous with the descent's landing on E, the piano reasserts B in the proper register (m. 16). In other words, the cadence in E major is arranged to emphasize that B does not resolve. This undercuts the cadence to E+ in the first stanza. It may be the strongest cadence to anything yet in the piece, but because B does not resolve, it is apparently a subordinate cadence. Thus at the beginning of the song the most apparent aspects of the LRP cycle (its cyclicity and common pitch) combine with the brevity of the stanza and its apparent sense in
, apparently in an inner voice (m. 13). As soon as this descent has arrived at E in measure 13, the piano reasserts the B in the same register. This B now initiates a fifth descent over an E pedal, and this time, simultaneous with the descent's landing on E, the piano reasserts B in the proper register (m. 16). In other words, the cadence in E major is arranged to emphasize that B does not resolve. This undercuts the cadence to E+ in the first stanza. It may be the strongest cadence to anything yet in the piece, but because B does not resolve, it is apparently a subordinate cadence. Thus at the beginning of the song the most apparent aspects of the LRP cycle (its cyclicity and common pitch) combine with the brevity of the stanza and its apparent sense in  minor to help us hear the
minor to help us hear the 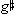 - at the beginning of the second stanza as a return to tonic.
- at the beginning of the second stanza as a return to tonic.
However, as the song continues through its second and third stanzas, we continue to move around the same LRP cycle. This continued motion around the cycle undercuts the sense of completion associated with the return of  . It is not unlike moving through a whole-tone scale. On the first completion of an octave there is a sense of completion, or "tonicity." However, with each additional step through the scale there is a similar sense of completion of an octave, and eventually we realize that no note is a better completion than any other note. Any point on the scale could serve equally well as a stopping point. A slightly tighter analogy may be to an octatonic scale. While we may prefer notes approached by half-step to notes approached by whole-step (or vice versa), there are still four such equivalent stopping points. With the LRP cycle, while we can distinguish between triads approached by L, R, or P, (although with less intuitive preference for any approach) we still have two of each. Thus the continued motion through the cycle undercuts the sense of completion achieved by the first trip around the loop.
. It is not unlike moving through a whole-tone scale. On the first completion of an octave there is a sense of completion, or "tonicity." However, with each additional step through the scale there is a similar sense of completion of an octave, and eventually we realize that no note is a better completion than any other note. Any point on the scale could serve equally well as a stopping point. A slightly tighter analogy may be to an octatonic scale. While we may prefer notes approached by half-step to notes approached by whole-step (or vice versa), there are still four such equivalent stopping points. With the LRP cycle, while we can distinguish between triads approached by L, R, or P, (although with less intuitive preference for any approach) we still have two of each. Thus the continued motion through the cycle undercuts the sense of completion achieved by the first trip around the loop.
At the same time that the continued cycling is undercutting the tonicity of 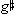 -, we are also beginning to realize that the song is stanzaic, that we have heard all the music we are going to, and that we are going to end in E major. We therefore reinterpret the fixed unit of music we have been hearing, the stanza, as presenting E major, and again two aspects of the LRP cycle help us do this.
-, we are also beginning to realize that the song is stanzaic, that we have heard all the music we are going to, and that we are going to end in E major. We therefore reinterpret the fixed unit of music we have been hearing, the stanza, as presenting E major, and again two aspects of the LRP cycle help us do this.
The first aspect is the opposite-mode arpeggiation. In E major we understand the motion through B+, G+, and E+ as V—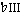 —I, or an opposite-mode arpeggiation of the tonic E. Thus, while focusing on the common tone B helped us hold onto the
—I, or an opposite-mode arpeggiation of the tonic E. Thus, while focusing on the common tone B helped us hold onto the 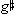 - tonic, focusing on the opposite-mode arpeggiation helps us reinterpret the stanza in E major. The other way the cycle helps us is by the fact that the e- triad is missing. We mentioned the b- triad that was interpolated between B+ and G+ and that helps make the motion around the cycle explicit. The fifth triad of the cycle, e-, is conspicuously absent (indeed, is replaced by the interpolated B7). This missing triad marks E+ as different from all the others in the cycle. As we travel around the cycle each triad is approached by its immediate predecessor except for E+. Even
- tonic, focusing on the opposite-mode arpeggiation helps us reinterpret the stanza in E major. The other way the cycle helps us is by the fact that the e- triad is missing. We mentioned the b- triad that was interpolated between B+ and G+ and that helps make the motion around the cycle explicit. The fifth triad of the cycle, e-, is conspicuously absent (indeed, is replaced by the interpolated B7). This missing triad marks E+ as different from all the others in the cycle. As we travel around the cycle each triad is approached by its immediate predecessor except for E+. Even 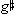 -, the first triad of the piece, is approached, as we cycle through the stanzas, by its predecessor, E+.
-, the first triad of the piece, is approached, as we cycle through the stanzas, by its predecessor, E+.
Because of the voice leading in the cycle, each triad moves to the next through the displacement of a single pitch. Because e- is missing, the motion from G+ directly to E+ involves two displaced pitches (D to E and G to  ). This is analogous to the traditional displacement of two pitches in the move from V to I, and indeed the interpolated B7 can help us hear the parallelism. E+ is therefore marked as unique in the cycle, and unique in a manner analogous to being preceded by V. Thus the use of the LRP cycle helps us finally hear E+ as the global tonic.
). This is analogous to the traditional displacement of two pitches in the move from V to I, and indeed the interpolated B7 can help us hear the parallelism. E+ is therefore marked as unique in the cycle, and unique in a manner analogous to being preceded by V. Thus the use of the LRP cycle helps us finally hear E+ as the global tonic.
Over the course of the song then, while the initial completion of the cycle and the unresolved common tone B help us hear the first stanza and at least the beginning of the second in  minor, and while the continued motion around the cycle begins to undercut the effect of
minor, and while the continued motion around the cycle begins to undercut the effect of  minor, the opposite-mode arpeggiation and the fact that e- is missing from the cycle help us to hear E+ as finally the global tonic. The song starts with a stanza understood in
minor, the opposite-mode arpeggiation and the fact that e- is missing from the cycle help us to hear E+ as finally the global tonic. The song starts with a stanza understood in  minor, and ends with the same stanza, now understood in E major. The repetition of that stanza focuses our attention on different aspects of the cycle, causing us to change our interpretation of the stanza, from
minor, and ends with the same stanza, now understood in E major. The repetition of that stanza focuses our attention on different aspects of the cycle, causing us to change our interpretation of the stanza, from  minor, to E major.
minor, to E major.
Together these two songs provide a good introduction to the possibilities opened up by neo-Riemannian relations. The harmonic motion of these songs, which is problematic in traditional theories, is intuitively simple with the neo-Riemannian operations (i.e., it traces simple patterns on the LRP map). Furthermore, by not having a well-defined tonic, these songs illustrate how the use of the neo-Riemannian operations can address compositional goals (creating the feeling that the parts belong together, and the feeling of completion at the end) usually addressed with a tonic. Finally, with the "orientations" in the RP cycle and the sustained common tone of the LRP cycle, these songs demonstrate that, despite the apparent focus on harmony, those operations also derive their interest from contrapuntal voice leading. These brief songs provide a useful means of addressing and overcoming the common resistances to transformational theory by offering accessible illustrations of some of the important and useful concepts in that theory.
References
Cohn, Richard. "As Wonderful as Star Clusters: Instruments for Gazing at Tonality in Schubert." Nineteenth-Century Music 22/3 (1999): 214-32.
_____. "Introduction to Neo-Riemannian Theory: A Survey and Historical Perspective." The Journal of Music Theory 42/2 (1998): 167-80.
_____. "Maximally Smooth Cycles and the Analysis of Late Romantic Triad Progressions." Music Analysis 15/1 (1996): 9-40.
_____. "Neo-Riemannian Operations, Parsimonious Trichords, and Their Tonnetz Representations." The Journal of Music Theory 41/1 (1997): 1-66.
Deutsch, Otto Erich. Schubert Thematic Catalog of all his Works in Chronological Order. New York: W.W. Norton, 1951.
Douthett, Jack, and Peter Steinbach. "Parsimonious Graphs: A Study in Parsimony, Contextual Transformations, and Modes of Limited Transposition." The Journal of Music Theory 42/2 (1998): 241-64.
Harrison, Daniel. Harmonic Function in Chromatic Music. Chicago: University of Chicago Press, 1994.
Hyer, Brian. "Tonal Intuitions in Tristan und Isolde." Ph.D. diss., Yale University, 1989.
Kochavi, Jonathan. "Some Structural Features of Contextually-Defined Inversion Operators." The Journal of Music Theory 42/2 (1998): 307-20.
Krebs, Harald. "Alternatives to Monotonality in Early Nineteenth-Century Music." The Journal of Music Theory 25/1 (1981): 1-16.
_____. "Third Relation and Dominant in Late 18th- and Early 19th-Century Music." Ph.D. diss., Yale University, 1980.
Lewin, David. "A Formal Theory of Generalized Tonal Functions." The Journal of Music Theory 26/1 (1982): 23-60.
_____. "Forte's Interval Vector, My Interval Function, and Regener's Common-Note Function." The Journal of Music Theory 21 (1977): 194-237.
_____. Generalized Musical Intervals and Transformations. New Haven: Yale University Press, 1987.
_____. Musical Form and Transformation: Four Analytic Essays. New Haven: Yale University Press, 1993.
Mooney, Michael Kevin. "The 'Table of Relations' and Music Psychology in Hugo Riemann's Harmonic Theory." Ph.D. diss., Columbia University, 1996.
Morris, Robert. "Voice-Leading Spaces." Music Theory Spectrum 20/2 (1998): 175-208.
Neue Schubert-Ausgabe, IV: Lieder, Band II. Bärenreiter-Verlag Kassel, 1999.
Santa, Mathew. "Nonatonic Systems and the Parsimonious Interpretation of Dominant-Tonic Progressions." Theory and Practice 28 (2003): 1-29.
Siciliano, Michael. "Neo-Riemannian Transformations and the Harmony of Franz Schubert." Ph.D. diss., University of Chicago, 2002.
1David Lewin, Generalized Musical Intervals and Transformations. Henceforth, GMIT.
2Richard Cohn, "Introduction to Neo-Riemannian Theory," provides a history of this approach, and the rest of that volume provides a sampling of approaches based on neo-Riemannian ideas.
3Richard Cohn, "As Wonderful as Star Clusters."
4Richard Cohn, "Maximally Smooth Cycles," illustrates this using the major third cycle on E major, exemplified by a passage from the Brahms Concerto for Violin and Cello (pp. 9-15).
5Cohn discusses this passage in much the same way in "As Wonderful as Star Clusters."
6David Lewin, GMIT, p. xi.
7David Lewin, "Forte's Interval Vector," 227ff. He mentions a "transformational attitude" on pp. 232-34.
8David Lewin, GMIT, and, in a less math-intensive presentation, Musical Form and Transformation. These books provide a convenient sampling of the many systems of transformations Lewin has explored.
9Richard Cohn, "Introduction to Neo-Riemannian Theory," is a good introduction to the variety of ideas and approaches subsumed by the rubric "neo-Riemannian Theory," and the entire issue of that journal provides an overview of that variety of approaches.
10Why Riemann called this relation a leading tone exchange is confusing, and in fact irrelevant to its current usage. Michael Kevin Mooney, in "The 'Table of Relations'," provides a good discussion of Riemann's system of triad relations, and of why the relation between C major and E minor should be a "Leittonwechsel" or "leading tone exchange." There are two ways to understand why Riemann called this relation a Leittonwechsel, both dependent upon his thoroughgoing harmonic dualism. In Riemann's dualism everything in minor is the inversion of the corresponding thing in major. Specifically, since a major triad is considered as being built of a major third and perfect fifth above a generating pitch (a root), a minor triad is considered as built of a major third and perfect fifth below the generating pitch (its "root"). Thus what we call E minor he would call B minor. This sounds counter-intuitive at first, but Lewin explores a variety of examples where it seems reasonable to hear minor triads in this way, in pp. 41-45 of "A Formal Theory." (A lengthier defense of Riemann's dualism can be found in Daniel Harrison, Harmonic Function.) In this context then, the relation between C major and E minor is a "leading tone exchange" because in each case the "root" (C in C major, B in E minor) moves to its leading tone (B in C major, C in E minor). The leading tone in minor is the inversion of the leading tone in major, and thus above the root. This understanding aligns best with Cohn's emphasis on maximally-smooth voice leading in, for instance, "Maximally Smooth Cycles," and it is implicit in Hyer's descriptions, for instance on p. 115 of "Tonal Intuitions." The other way of construing it, found in Mooney, "The 'Table of Relations'," is that there is a consistent "Wechsel" operation that exchanges the two triads that share a "root," for instance C major and F minor. A "Leittonwechsel" would then be a "Wechsel" followed by transposition to the leading tone. Thus C major is transformed to its "Wechsel" F minor (which he would call "C minor"), which is then transposed to the leading tone of C, "B minor," which we would call E minor. Conversely, E minor (which he would call B minor) is transformed to its "Wechsel" (B major) which is then transposed to the leading tone of "B minor," C major. As I said above, this is all irrelevant to its current usage. In neo-Riemannian theory, "L" is simply the third way, along with P and R, of relating two triads that share two pitches.
11Such a map can also be derived from various "Tonnetze," maps of relations among pitches or pitch classes that were of interest to some nineteenth-century theorists and have attracted recent attention. The main difference is that Tonnetze are maps of pitch relations, while this map is a map of triad relations. For a history of such Tonnetze, see Mooney, "The 'Table of Relations';" for a discussion of the relation between this map and Tonnetze see Michael Siciliano, "Neo-Riemannian Transformations;" some aspects of the relation are treated more formally in Robert Morris, "Voice-Leading Spaces."
12Lewin, GMIT, 176-77.
13Brian Hyer, "Tonal Intuitions," pp. 196-99, describes the way such a map rolls back on itself but does not use the word "torus." Cohn describes it explicitly as a torus in "Neo-Riemannian Operations," pp. 17-20. More recently, Jack Douthet and Peter Steinbach, "Parsimonious Graphs," discuss the geometry and try to draw a picture of such a torus, which they call a "chicken wire torus."
14David Lewin, "A Formal Theory." Also, Jonathan Kochavi, "Some Structural Features," discusses them in a more formal setting.
15Specifically, I4 will again relate C to E, and A to G, but also F to B, thus relating F+ (F, A, C) to e- (E, G, B).
16Richard Cohn, "Maximally Smooth Cycles," provides the most thorough exploration of such voice leading. Recently, Mathew Santa, "Nonatonic Systems," explores relations between triads and incomplete seventh chords using maximally smooth voice leading.
17Harald Krebs, "Third Relation and Dominant," examines third relations in the standard Classical and early Romantic repertoire and thus provides a nice catalog of such works. He also provides Schenkerian reductions and discussions of most of these works.
18These discussions, of course, do not intend to present exhaustive analyses of every aspect of these songs, merely to show how the neo-Riemannian operations can help us understand otherwise problematic harmonic choices. I therefore mostly avoid discussing relations between the text and music.
19The Neue Schubert-Ausgabe gives the duet as the first version (pp. 108-9) and the solo as the second version (pp. 110-12). Similarly, Otto Erich Deutsch, Schubert Thematic Catalogue, 239, says the duet came first and the solo version is the alternate. As with most such interpretations the argument is symmetrical. I will argue that the changes made in the solo version are to compensate for the sense of completion lost by transposing the ending and disrupting the RP cycle. If in fact the solo version came first, then the same changes would reflect the enhanced sense of completion achieved by following the RP cycle.
20The E in m. 7 is merely reminding us of the original register of "the voice that started on E." The more "structural" 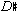 to which it resolves (m. 8, pn., rh) is of course a larger level motion within that same voice.
to which it resolves (m. 8, pn., rh) is of course a larger level motion within that same voice.
21The repetition of lines of text among the stanzas, resulting in the first line being set to each of the four lines of music, positively begs speculations about text-music relations.
22Richard Cohn, "Neo-Riemannian Operations," pp. 42-45.
23"Consonant support" is used here by analogy to Schenkerian analysis. As with the orientations in the previous analysis it says nothing about the position of the triads. It means merely that the LRP cycle provides a context in which a single pitch-class can be accompanied by each of the six consonant triads in which it occurs.
24Harald Krebs, "Alternatives to Monotonality," describes "Trost" from a Schenkerian perspective as in E major, and asserts that there is a descent from 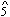 in the last measures. As I discuss later, I can not find a descent with appropriate support from B.
in the last measures. As I discuss later, I can not find a descent with appropriate support from B.
25This is easiest to hear if you listen without the score. The score visually emphasizes that this is all the music there is and that it ends in E major, in a way that could not be aurally present but that inevitably influences our hearing. I recommend listening without the score but thinking about where tonic is, until about the third stanza, at which point most people will have shifted to hearing the stanza in E major and seeing the score will not unduly influence them.
26For instance, think of the second themes of the C Major Quintet, D. 956, or the G Major Quartet, D. 587. And, if it seems too early in the piece to move to a "second theme," think of the move to 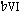 in the first theme of the B-flat Sonata, D. 960.
in the first theme of the B-flat Sonata, D. 960.


