The subject of musical contour has received a growing amount of attention in recent years.¹ In part this stems from a recognition that contour is one of the features that most engage a listener; a melody's shape is often more memorable than its specific pitch or interval content.² In this essay, I will focus on contour in two homophonic works by Anton Webern: the fifth of the Bagatelles for String Quartet, op. 9 and the second of the Five Movements for String Quartet, op. 5. Each analysis will begin by focusing on contour as a quasi-motivic element, making particular use of Robert Morris's contour reduction algorithm. Then, the pitch structure of each work will be examined with reference to the contour analysis. While the contour-specific portions of the analysis illustrate the extent to which contour recurrence itself is an organizing feature of these melodies, contour recurrence often serves to highlight pitch motives.

I have chosen to focus on homophonic works for two reasons. First, in homophonic works there is a greater opportunity to examine longer strings of pitches. In many of Webern's more contrapuntal works, motives are only two or three notes long; such small segments exhibit a smaller variety of contours (so the relationships are less significant). Second, homophonic works highlight Webern's practice of writing melodies that begin in one instrument and move to other instruments; these resulting longer contours are of particular interest.

 

I. op. 9, no. 5

When discussing the fifth of Anton Webern's Bagatelles for String Quartet, op. 9, analysts have tended to emphasize interval-class-1 relations in explaining its construction. In his article, "Chromatic Completion: Its Significance in Tonal and Atonal Contexts," Paul Paccione asserts that "[t]he generating interval for the fifth movement is the minor second."³ This is particularly evident in what Paccione identifies as the first section of the work, mm. 1-7, in which, as can be seen in Example 1 (a modification of Paccione's Example 6), the aggregate is formed, with semitone relations governing the introduction of new pitches.

 

Example 1. Semitone connections in mm. 1-6.

 

Paccione's second section of the piece (mm. 7-12) also contains an aggregate in which each new pitch-class participates in an audible ic-1 relation.

Richard Chrisman, in his article "Anton Webern's 'Six Bagatelles for String Quartet,' op. 9: The Unfolding of Intervallic Successions," analyzes the entirety of op. 9 similarly emphasizing ic-1 relations.⁴ Chrisman is particularly concerned with structures of the form "semitone/unspecified interval/semitone," that is, two semitones separated by some interval. This basic structure, derived from Walter Kolneder's work, represents the beginning of two "semitone chains;" a fifth note would form a semitone (or some other interval belonging to ic 1) with one of the initial four, and later notes would link with one or the other chain in a similar manner.

The observations concerning the prevalence of interval-class 1 illuminate an important aspect of coherence in op. 9, no. 5. However, without directly challenging these observations, I would like to propose an alternative view of the bagatelle, founded on theories of contour, with particular emphasis on Robert Morris's contour reduction algorithm. In analyzing the bagatelle, I will begin with a premise not discussed in either Paccione's or Chrisman's analyses, namely that there are points in the piece in which there are two distinct textural layers, a melody and an accompaniment.⁵ Example 2 separates the layers. The next two paragraphs explain certain choices made concerning melodic and non-melodic notes in Example 2. The reader who wishes to accept the example and proceed directly to the analysis proper may skip ahead.

 

Example 2. Melody and accompaniment of op. 9, no. 5.

 

In mm. 1-5, the division between melody and accompaniment is self-evident. Measures 6 and 7 present more of a problem. For instance, in m. 6 there may be some disagreement about the choice of the second violin's 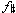', rather than the viola's 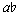', as melodic. There are, indeed, two good reasons to choose the 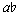'. First, the viola has had the previous melodic note, c'', in m. 5, and there are no notes between this c'' and the 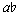'. Second, the 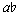' is played arco, while the simultaneously-attacked g' in the 'cello and the following 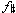' in the violin 2 are played am Steg; the timbral difference could contribute to the isolation of the 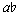'. The main reason for considering the 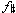' the melodic note is this: up to and following this point we do not have one melodic tone attacked simultaneously with one accompanimental pitch. This is not to say that melodic and accompanimental pitches are never simultaneously attacked; indeed, this happens in m. 1. Nor is it being suggested that all accompanimental pitches must be attacked in groups of two or more. Rather, the assertion is that where two or more notes enter together, at least two are accompanimental. In mm. 4-6, individually-attacked notes alternate with simultaneities (Example 3); thus, we (should) perceive the single notes and the simultaneities as operating on different textural levels. Through this pattern the second violin's 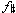' becomes more individuated, and, thus, more "melodic" than the viola's 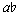'. The 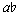' does, however, emerge as melodic in m. 7, before moving to 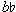'; I have analyzed this passage as a codetta to part one.

 

Example 3. Melody and accompaniment in mm. 4-6 of op. 9, no. 5.

COPYRIGHT NOTICE: Webern, SIX BAGATELLES FOR STRING QUARTET, OP. 9. Copyright 1924 by Universal Edition A.G. Wien. Copyright renewed. All rights reserved. Used by permission of European American Music Distributors Corporation, sole U.S. and Canadian agent for Universal Edition.

 

The dyad in m. 11 is considered accompanimental, since the notes are at the same dynamic, and are attacked at the same time and in the same manner (pizz.); there is no basis for asserting either one as melodic. I have analyzed the two notes of m. 12 as melodic, since they are attacked alone, but their melodic significance is by no means self-evident. Finally, in m. 13, I have considered the viola to be melodic (it has the motion), while the other instruments are accompanimental. A special effort must be made by the performers to bring out the viola's -d '', but, given the tenuto marks on the viola notes (while the other instruments are marked staccato) and the obvious relations between this dyad and the 'cello's d-'' in m. 9, Webern seems to have intended the viola part to stand out in m. 13.

Having separated the texture into melody and accompaniment, we need to discuss the form of the piece a bit more carefully before examining contour, since the segmenting of contours will depend in part on formal considerations. The piece comprises four phrases: 1) m. 1 through m. 4, bt. 1; 2) m. 4, bt. 1 through m. 7; 3) mm. 8-10; and 4) mm. 11-13. The large division is at m. 7; the two parts of the binary form are distinguished most obviously by the density of sound. The texture is thicker in mm. 1-7, and there are more sustained notes; mm. 8-13 contain fewer simultaneous attacks, and the notes are generally shorter.

The melody of the first part of the piece (including the codetta) can be divided into four small contours, two <021> contours surrounded by two <01> contours (Example 4a). It should be noted that the two <01> contours are both ascending M2nds. Alternatively, we can view the opening two notes as initiating a <021> contour. The melody proper (mm. 1-6) could then be analyzable as three <021> contours, with the first two overlapping (Example 4b).⁶

 

Example 4. Contour segments in part one.

 

Part two has more melodic content than part one (Example 5).

 

Example 5. Contour segments in part two.

 

Indeed, only the dyad in m. 11 and the violins and 'cello in m. 13 are considered accompanimental. Whereas in part one contour <021> was featured, in part two contour <102> (the retrograde-inversion of <021>) predominates.⁷ Phrase 3 (mm. 8-10) can be seen as being built from two <102> contours surrounding a <01> dyad (Example 6).

 

Example 6. Reduced contours in op. 9, no. 5.

 

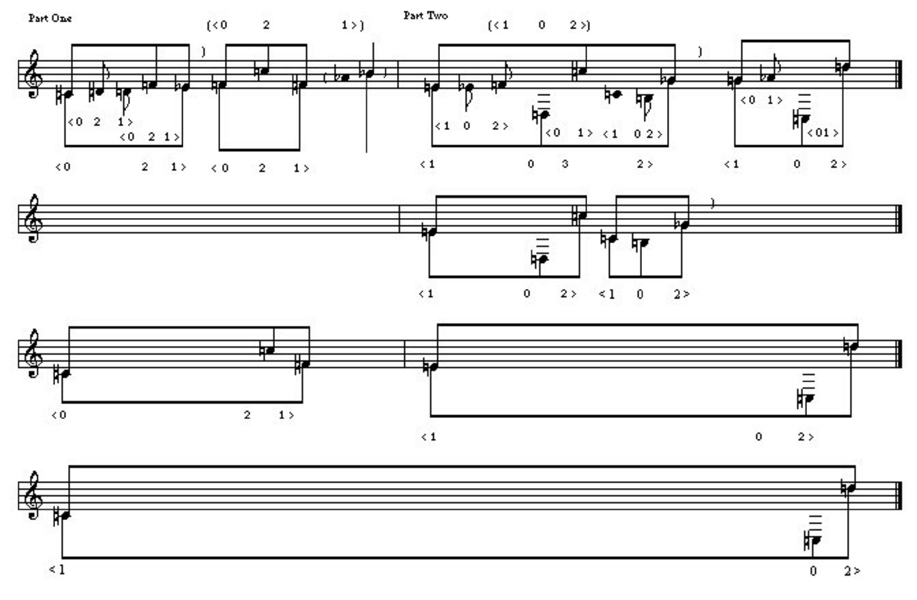
Just as the '-' <01> dyad of m. 1 could be combined with the following d ' to make a <021> contour (the foundation of part one), the d-'' <01> dyad of m. 9 can be combined with the preceding f ' to make another <102> contour (this is shown in parentheses above the example).⁸ The phrase 4 melody consists of two <01> dyads. The <01> contours are marked between the staff and the lower beam.

While we see a degree of contour consistency on the local level in both parts of the bagatelle, we can also examine contours from a broader perspective by employing Robert Morris's contour reduction algorithm. Briefly, the algorithm involves selecting those notes that are at least as high as those immediately surrounding (maxima) and those that are at least as low as those immediately surrounding (minima). Notes that are neither maxima nor minima are reduced out. The algorithm is then applied separately to the collection of maxima (the max-list) and the collection of minima (the min-list); our interest is confined to maxima within the max-list and minima within the min-list. The algorithm is applied repeatedly until neither the max-list nor the min-list can be further reduced. The lists are then recombined to give the contour's prime form. The beginning and ending notes of a contour are by definition both maxima and minima and are included in the prime form.⁹ Example 6 applies the algorithm to the melody of op. 9, no. 5. As shown in the example, not only can the first phrase be seen as being built from overlapping <021> contours, but the phrase as a whole reduces to <021> (this is shown on the top staff of the example, below the lower beam). The prime form of phrase 2 is also <021>. Furthermore, if we view the complete melody of part one (phrases 1 and 2 combined) as a single contour, it, too, reduces to <021> (the third staff of the example).¹⁰ Thus, <021> is operative on three distinct levels of structure in part one.

As discussed above, the surface of phrase 3 is largely devoted to <102> contours; <102> can also be seen in deeper levels. Remember, phrase 3 can be seen as comprising three <102> contours, with the first two overlapping. Put together, these overlapping segments reduce to a <102> contour; this is shown in the second staff of Example 6. The complete phrase 3 melody does not form a <102>, though; its prime form is <1032>. However, the two dyads of phrase 4, when combined, do produce a <102> reduced contour. Furthermore, the melody of mm. 8-13 as a whole forms a <102>. Finally, <102> is the reduced contour of the melody of the complete bagatelle (the bottom staff of Example 6).

As mentioned before, much has been made of semitone (ic-1) relations in this bagatelle. On the basis of contour analysis (including the separation of the texture), we can now revise that view somewhat. As is shown in Example 2, the accompaniment is quite unified: only the [0,1,2] set of m. 7 is neither a member of Forte's set class 3-4 ([0,1,5]/[0,4,5]) nor a subset of it.¹¹ Example 7 gives the melody of part one, divided into segments on the basis of our contour analysis. By separating the texture into melody and accompaniment, we will be able to see to what extent intervals other than ic 1s are featured.

 

Example 7. Interval expansion in <021> contours of part one.

 

Surprisingly, there is only one adjacent semitone in the melody of part one, between ' and d ' in mm. 1-2, and even this is mitigated by the intervening rest and the initial impression that these notes belong to different contour segments. However, all three of the <021> local contours (including the alternative reading of the first three notes) have a semitone between contour elements 0 and 1 (the first and third notes of the segments). To go along with this constant semitone between the first and last notes, Webern creates a pattern of intervallic expansion between the first and second notes of each <021> segment. In the opening <021> ('-'-d ') there is a M2nd between elements 0 and 2; in the overlapping <021> (d '-f '-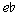'), this is expanded to a m3rd. In the final <021> (f '-c'-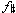'), the opening interval is a P5th. So, we have interval expansion in the 0-2 interval, but the 0-1 framing interval is always a semitone.

In the second part of the bagatelle, the ic-1 relations are made more explicit. We can see this by comparing phrases 1 and 3. The first seven pcs of phrase 1 (including the accompanimental notes) and the first seven pcs of phrase 3 are the same, {B, C, , D, 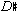, E, F}.¹² Though this is a completely chromatic set, to repeat, there is only one melodic semitone in phrase 1; however, in phrase 3 there are four adjacent ic 1s in the melody. So, in terms of pitch material, phrase 3 is going over the same territory as phrase 1, but emphasizing ic-1 relations more explicitly.

Part two exhibits a progression of intervals similar to that seen in part one (Example 8).

 

Example 8. Interval expansion in <102> contours of part two.

 

Part two begins with a <102> contour. Like the initial <021> contour of the melody of part one ('-'-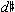d '), this trichord (e'-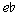'-f ') is a [0,1,2] set; in part one a whole step ('-'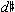) is presented, then filled (with d '), whereas in part two a note (e') is presented, then surrounded by a whole step (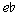'-f '). In part one the third note (the end of the first <021> and the beginning of the overlapping second <021>) is a D (d '), which is immediately followed by an F (f ''). In part two, the third note, the end of the first <102> and the beginning of the overlapping second <102>, is an F (f '), and is immediately followed by a D (d). The third <021> of part one (phrase 2) is a [0,5,6] set, with a P5th between contour elements 0 and 2. The third <102> of part two is also a [0,5,6] set, also with a P5th between contour elements 0 and 2.

In summary, while Paccione, Chrisman, and others have shown ic-1 relations on the surface of the bagatelle, we can see that many of these are the result of measuring intervals between non-adjacent notes or notes on distinct layers of texture. But more significantly, the analysis has shown that Webern's melody is built from two distinct contours, utilized on multiple levels of structure.

 

II. op. 5, no. 2

The second of Webern's Five Movements for String Quartet, op. 5 is a somewhat more complex work than op. 9, no. 5.¹³ The work is a rounded binary. The opening until the fermata in m. 1 is an introduction. Phrase 1 comprises m. 1, bt. 3 through m. 2, bt. 2; the melody of the phrase ends with the f ' in the viola. Phrase 2 goes from m. 2, bt. 3 through m. 4, bt. 1; the remainder of m. 4 through m. 5, bt. 2 is a codetta to part one.

Part two starts at m. 5, bt. 3. The "B" section comprises phrases 3 and 4 (mm. 5-10). The phrase 3 melody is in the violin 2, m. 5, bt. 3 through m. 6. The phrase 4 melody begins in the violin 1 in the middle of m. 7; the phrase continues to the downbeat of m. 10. Phrase 5 (the A' section) comprises m. 10 to the downbeat of m. 12, with mm. 12-13 constituting a codetta to Part Two.

All of the phrases in the two A sections (phrases 1, 2, and 5) exhibit overlapping <120>/<021> contours; this can be seen in Example 9.

 

Example 9. Overlapping <120>/<021> contours in A and A' sections of op. 5, no. 2.

 

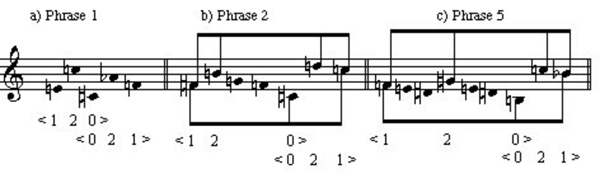
In phrases 2 and 5, the beginning segment, the <120> contour, is embellished (phrases 2 and 5 are very closely related motivically). By "embellished" I mean something along the lines of a Schenkerian reduction. The embellishing tones are those that are unstemmed, being neither minima nor maxima. This analysis represents a view of contour structuring in between the surface and the Depth One-reduction that results from Morris's algorithm. Consider the first phrase. It is by no means self-evident that this five-note melody should be seen as two contours. Furthermore, using the contour reduction algorithm will not suggest a separation; since every note in the melody is either a maximum or a minimum pitch, no pitches are eliminated from Depth 0 to Depth 1 (Example 10). It is at Depth 2 that we achieve the prime form, <1302>.

 

Example 10. Reduction of phrase 1 melody of op. 5, no. 2.

 

While an analysis employing two contours does not immediately suggest itself in phrase 1, it seems more plausible in phrase 2. In phrase 2 the two notes that are neither maxima nor minima at Depth 0 are represented together, between the maximum b' and the minimum '. By highlighting the fact that it is only the first part of the melody that is subject to immediate reduction, the algorithm indirectly suggests analyzing the reducible and the irreducible sections as separate, but overlapping contours. Phrase 5 (the A' section) is motivically related to phrase 2 (Example 11). Although it has a descending chromatic line from f ' to 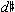' that precedes the "transposed restatement" of phrase 2, phrase 5 still reduces to the same <1032> contour as phrase 2.

 

Example 11. Motivic relationships between phrases 2 and 5 of op. 5, no. 2.

COPYRIGHT NOTICE: Webern, 5 MOVEMENTS FOR STRING QUARTET, OP. 5. Used with kind permission of European American Music Distributors LLC, U.S. and Canadian agent for Universal Edition, Vienna.

 

The phrases of the B section are more complex. The phrase 3 melody has within it a clear motivic relationship to phrase 1 (Example 12).

 

Example 12. Motivic relationships between phrases 1 and 3 in op. 5, no. 2.

COPYRIGHT NOTICE: Webern, 5 MOVEMENTS FOR STRING QUARTET, OP. 5. Used with kind permission of European American Music Distributors LLC, U.S. and Canadian agent for Universal Edition, Vienna.

 

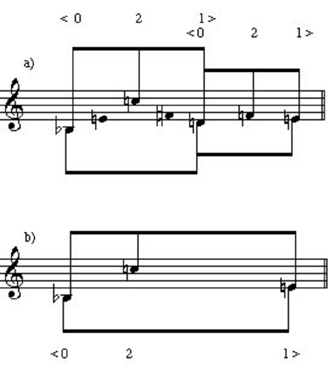
Thus, it would seem that an overlapping <102>/<021> analysis could be invoked here. But, despite the motivic relationship, it does not seem proper to omit the opening 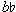of the melody in considering the contour. Keeping the idea of the overlapping contours but including the 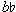in the first segment results not in <102>/<021> contours, but two overlapping <021> segments (Example 13a). Furthermore, the phrase as a whole reduces to <021> (Example 13b).

 

Example 13. <021> reduced contours in phrase 3 of op. 5, no. 2.

 

While phrase 3 is closely related to phrase 1 and suggests being reduced to the same <120>/<021> contour, phrase 4 is closely related to phrase 2 and comes even closer to mimicking its contour structuring. The opening rise and fall of phrase 4 leads one to anticipate a <120>/<021> contour, or (at least) the <120> segment. However, the descent does not go far enough; it simply returns to the opening a', thus making the contour <010>, or, to reflect our anticipation, <121>. The melody then seems to enter the <021> phase of the <120>/<021> contour prematurely, and with an interval (a M3rd, a'-'') far too small to confirm the anticipated phrase 2 analogy. This M3rd is echoed in the 'cello (as if the 'cello is pointing out the "mistake" that the violin has just made). The violin 1 tries to rectify the situation in two ways: it reaches a note below the a', g', to complete the anticipated <120> portion of the contour, then presents a rising interval, a M6th, that gets somewhat closer to the m9th of the <021> segment of phrase 2 (Example 14).

 

Example 14. Reduced contour of phrase 4, op. 5, no. 2.

 

There is a possibility now of completing the <120>/<021> contour, but Webern does not realize it; instead, the 'cello again echoes the violin 1 (a suggestion that the M6th is still not adequate for a convincing restatement of phrase 2). Thus, we can describe phrase 4 with the contours <120>/<02?>.

An alternative reading of phrase 4 would view it as comprising, like phrase 3, two overlapping <021> contours, of which the second is incomplete in two attempts (Example 15).

 

Example 15. <021>/<02?> contours in phrase 4 of op. 5, no. 2.

 

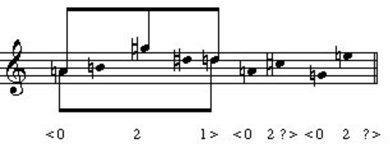
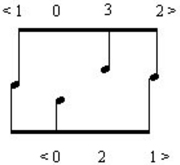
I prefer the first analysis because of an intervallic connection between phrases 2 and 4 (Example16).

 

Example 16. Tritones in phrases 2 and 4 of op. 5, no. 2.

 

In the diminution of the <120> portion of the contours of both phrases, we see interlocking tritones. The second tritone signals the beginning of the <021> segment of the longer contour in phrase 2. I think that the overlapping tritones are audible, so I prefer not to divide the phrase 4 melody after the d '', as required by the alternative reading.

Example 17 gives the reduced contours for the larger sections of the piece (A', of course, consists only of phrase 5).

 

Example 17. Reduced contours in op. 5, no. 2.

 

As can be seen, <1032> is the contour not only for phrases 2 and 5 separately, but also the whole A section and the melody of the entire movement. The B section as a whole reduces to <021>. So, while the A sections feature <1032> contours, the B section focuses mostly on a <021> subsegment (Example 18; the full <1032> is shown above the example, while the <021> subset is shown below).

 

Example 18. <021> as subset of <1032>.

 

While Webern has tightly constructed his melodies for op. 5, no. 2 in terms of contour (especially via the <102>/<021> segments), he realizes these contours with a variety of pc sets. The underlying pitch principle of the work is the resolution of an opposition between the whole-tone and chromatic spheres. The contour analysis helps to show how the whole-tone aspects gradually become prominent in the melody, appearing first as diminutions (shown by the reduction algorithm) and progressing to deeper levels.

In the Introduction, the chromatic and whole-tone spheres are clearly separated. The viola melody is a [0,4,6] set, while the accompanying chord is [0,3,6,7]. With the beginning of the main body of the work, these roles are reversed: the melody of phrase 1 is non-whole-tone, both on the surface and in the reduction (the set of the reduced contour is [0,1,4,5]), while the accompanying chord is a whole-tone set ([0,4,6]). In phrase 2 the chords remain [0,4,6] sets and the melody again reduces to a non-whole-tone set, [0,1,2,6]. The sets [0,1,4,5] and [0,1,2,6] are similar in that both can be constructed from two ic 1s and an ic 4; the ic 4 falls in analogous positions in the phrases, between contour elements 1 and 3 (Example 19).

 

Example 19. ics 1 and 4 in phrases 1 and 2 in op. 5, no. 2.

 

But, whereas phrase 1 had no contour diminutions at depth 0, in phrase 2, the passage from b' to ' is diminuted with g' and f '. The diminutions create overlapping [0,2,6]/[0,4,6] sets; in this way, the whole-tone sphere makes its first appearance in the melody proper of the work. The codetta of part one is chromatic.

The melody of phrase 3 is predominately whole-tone. It reduces to a [0,2,6] set (Example 20); [0,2,6] is also used twice on the surface of the melody.

 

Example 20. [0,2,6] sets in phrase 3 of op. 5, no. 2.

 

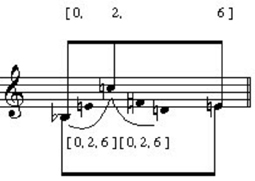
There is only one melodic note that does not belong to the whole-tone scale on C, f '; this note can easily be heard as a chromatic passing tone within a whole-tone setting. The accompaniment to phrase 3, by contrast is mostly chromatic. In m. 6, there is an accompanimental augmented triad, but its whole-tone implications are offset by virtue of its belonging to the scale on , rather than to the C-scale of the melody.

While phrase 3 can be seen as obviously based on the whole-tone scale (both on the surface and with respect to the reduction), phrase 4 represents a subtle merging of the whole-tone elements back into a chromatic setting. The melody reduces to a [0,3,4,5] set. Since this is a set that has two ic 1s, we might posit a connection to phrases 1 and 2. However, the phrase 4 melody can also be analyzed with reference to [0,2,6] trichords. Example 21 separates the melody into three [0,2,6] sets.

 

Example 21. [0,2,6] sets in phrase 4 of op. 5, no. 2.

 

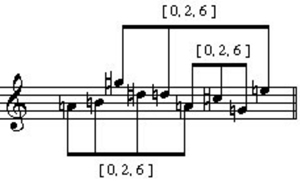
The segmentation here is rather odd. I think that the (a',b',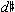'') and (g',a','') sets can be heard with little difficulty. In the case of (g',a','') the notes are consecutive (though they cross motivic boundaries). With the (a',b',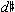'') set, the a' and b' are consecutive, and we have already associated the 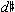'' with the following a' as part of the overlapping tritones. By combining the (a',b') and (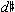'',a') dyads, we get the [0,2,6] set. The overlapping tritones, of course, would lead us to connect 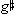'' and d '' of the third [0,2,6], but it seems difficult (if not impossible) to perceptually carry the ending e'' back to the tritone. Although the segmentation is clumsy, it still remains conceivable that the passage may have been composed via the three [0,2,6] sets.

The ostinato in the violin 2 that accompanies the phrase 4 melody can also be considered whole-tone derived. The M2nd 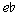'-f ' belongs to the same whole-tone collection as the opening a'-b' of the melody. Just as the melody as a whole is chromatic (the [0,2,6] sets do not belong to the same whole-tone scale), the violin 2 becomes chromatic in m. 9, when the 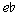'-f ' whole step is chromatically filled. Phrase 4 can, thus, be interpreted as using the whole-tone elements, but hiding them within a chromatic context. Furthermore, the whole-tone aspect is still evident in the complete B section; the reduced melody forms a [0,4,6] set (Example 22).

 

Example 22. [0,4,6] in contour reduction of B section of op. 5, no. 2.

 

Phrase 5 confirms the chromatic sphere as firmly triumphant. Both melody and accompaniment are unambiguously chromatic (rather than whole-tone). Interestingly, however, the reduced melody for the entire work is a [0,4,6] set (refer back to Example 17).¹⁴ Thus, during the main body of the piece, the whole-tone scale is absent from the melody of phrase 1, present in the diminutions only of phrase 2, dominant in phrase 3, more subtly present in a chromatic context in phrase 4, and absent again in phrase 5; but phrase 5, by ending on a 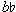' confirms the [0,4,6] set on the deepest level, as "predicted" by the whole-tone melody of the Introduction.

 

Conclusion

These two homophonic works help to illustrate how Webern structures his melodies by contour. Morris's contour reduction algorithm shows that Webern utilizes particular shapes on several distinct hierarchical levels. We often find that a specific contour is presented in a number of different intervallic guises, while still retaining its integrity. By focusing our attention on contour, we may find that works that we thought had been exhausted (like op. 9, no. 5) have further secrets to reveal, and that works the pitch structure of which do not appear to be satisfactorily economical (like op. 5, no. 2) may open to us more fully.

 

References

Archibald, Bruce. "Some Thoughts on Symmetry in Early Webern: op. 5, no. 2." Perspectives of New Music 10 (1972): 159-63.

Chrisman, Richard. "Anton Webern's 'Six Bagatelles for String Quartet,' op. 9: The Unfolding of Intervallic Successions." Journal of Music Theory 23 (1979): 81-122.

Clifford, Robert. "Contour as a Structural Element in Selected Pre-serial Works by Anton Webern." Ph.D. diss., The University of Wisconsin-Madison. 1995.

Freedman, Eric G. "The Role of Diatonicism in the Abstraction and Recognition of Contour and Interval Information." Music Perception 16 (1999): 365-87.

Friedmann, Michael. "A Methodology for the Discussion of Contour: Its Application to Schoenberg's Music." Journal of Music Theory 29 (1985): 223-48.

. "A Response: My Contour, Their Contour." Journal of Music Theory 31 (1987): 268-74.

Kolneder, Walter. Anton Webern: An Introduction to His Works, trans. Humphrey Searle. Berkeley and Los Angeles: University of California Press. 1968.

Lewin, David. "Transformational Techniques in Atonal and Other Music Theories." Perspectives of New Music 21 (1983): 312-71.

Marvin, Elizabeth West. "A Generalized Theory of Musical Contour: Its Application to Melodic and Rhythmic Analysis of Non-Tonal Music and its Perceptual and Pedagogical Implications." Ph.D. diss., University of Rochester, Eastman School of Music. 1988.

. "A Generalization of Contour Theory to Diverse Musical Spaces: Analytic Approaches to the Music of Dallapiccola and Stockhausen." In Elizabeth West Marvin and Richard Hermann (eds.) Concert Music, Rock, and Jazz Since 1945: Essays and Analytic Studies (pp. 135-71). Rochester, NY: University of Rochester Press. 1995.

Marvin, Elizabeth West and Paul Laprade. "Relating Musical Contours: Extensions of a Theory for Contour." Journal of Music Theory 31 (1987): 225-67.

Morris, Robert D. Composition with Pitch-Classes. New Haven: Yale University Press. 1987.

. "New Directions in the Theory and Analysis of Musical Contour." Music Theory Spectrum 15 (1993): 205-28.

Paccione, Paul. "Chromatic Completion: Its Significance in Tonal and Atonal Contexts." College Music Symposium 28 (1988): 85-93.

Quinn, Ian. "Fuzzy Extensions to the Theory of Contour." Music Theory Spectrum 19 (1997): 232-63.

. "The Combinatorial Model of Pitch Contour." Music Perception 16 (1998): 439-56.

Schmuckler, Mark A. "Testing Models of Melodic Contour Similarity." Music Perception 16 (1999): 295-326.

Vander Weg, John D. "Symmetrical Pitch- and Equivalence-Class Set Structure in Anton Webern's Opus 5." Ph.D. diss., The University of Michigan. 1983.

---

¹Much material in this essay was presented in two different talks, at the 1995 meeting of the Texas Society for Music Theory (Austin, TX) and the 1996 meeting of Music Theory Midwest (Kalamazoo, MI). The main theoretical apparatus for contour study was developed in the mid-1980s by Robert Morris (Composition with Pitch-Classes), Michael Friedmann ("A Methodology for the Discussion of Contour;" and "A Response"), and Elizabeth West Marvin and Paul Laprade ("Relating Musical Contours"). Extensions by Morris ("New Directions"), Marvin ("A Generalization of Contour Theory") and Ian Quinn ("Fuzzy Extensions"), in particular, have enriched the study of contour in the pitch dimension.

²Particularly good summaries of perception studies of contour can be found in Marvin, "A Generalized Theory of Musical Contour," 31-47; Quinn, "Combinatorial Model;" and Schmuckler, "Testing Models." See also Freedman, "Role of Diatonicism."

³Paccione, "Chromatic Completion," 90.

⁴Chrisman, "Anton Webern's 'Six Bagatelles for String Quartet.'"

⁵Not separating the texture is not the result of a lack of consideration by other theorists; Chrisman, for instance, identifies as one of the virtues of Allen Forte's work that "his analyses proceed from the total melodic and chordal content of a passage, rather than from a selection of pitches chosen to show structural relationships" ("Anton Webern's 'Six Bagatelles for String Quartet,'" 84).

⁶Robert Clifford discusses contour segmentation issues in his dissertation, "Contour as a Structural Element;" see pp. 38-50, especially pp. 47-50. He calls a combination of two segments a compound segment, though he does not invoke overlaps in his segmentations.

⁷Since these contours are RI-related, Morris places them in the same c-space segment class (or csegclass). A csegclass collects all contours related by identity, translation, retrograde, inversion, and retrograde-inversion. See Morris, Composition with Pitch-Classes, 32-33 and Marvin, "A Generalized Theory of Musical Contour," 76-80.

⁸This is by no means the most intuitive segmentation, but the f ' and the d that follows are both played pizz.

⁹Morris, "New Directions," 212-13.

¹⁰This is true regardless of whether we take the 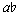'-'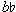 of m. 7 to be part of the melody proper or we end the melody with the preceding '.

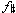¹¹In this paper, sets will be labelled by their Tn-type, rather than by their Tn/TnI-type.

¹²To carry the analogy a step further, the eighth pc of Phrase 3 is 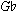; in Phrase 1 the eighth and ninth pcs ( 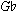and ) enter simultaneously.

¹³For analyses of op. 5, no. 2 see David Lewin, "Transformational Techniques;" John D. Vander Weg, "Symmetrical Pitch- and Equivalence-Class Set Structure;" and Bruce Archibald, "Some Thoughts on Symmetry."

¹⁴There is, of course, a danger in making an assertion about pitch structure based on the contour reduction algorithm over such a large passage (roughly two minutes worth of music). About his reduction of the "entire" melody of Schoenberg's op. 19, no. 4 as a single contour, Morris comments that the results "are not very revealing" ("New Directions," 217). That this largest reduction may be dismissed as irrelevant does not, thereby, invalidate the progression of whole-tone elements through the separate phrases.