Introduction
Canonic writing has been part of the education of music students for centuries. Considered a routine means of elaborating primary musical material in the Renaissance,2 it maintained an important place in the didactic writings of later periods. Yet perusals of historical treatises as well as modern counterpoint texts usually reveal very little information about how to compose a canon apart from a step-by-step approach involving writing a short amount of material in one part, copying it into a second part after a predetermined time distance, finding suitable material to continue the first part, and repeating this process until the end of the piece. This general prescription for writing canons has survived intact in many historical sources3 and in pedagogical texts up to the present day.4 In most cases, little additional assistance is offered to students apart from general comments on common difficulties encountered in strict imitative writing, such as the potential for monotony in canons at the unison or octave, crossing of parts in unison canons, exact versus inexact intervallic imitation in non-unison canons, and forming cadences. Modern authors often provide surveys of the different subtypes of canon and include a wide range of repertoire examples.5 While such surveys are very useful to students in situating canonic writing in the history of Western music and demonstrating some of the levels of complexity and ingenuity within this tradition, they do not provide structured teaching material for guiding students through the processes and difficulties involved in writing different kinds of canon.
It is reasonable to believe that composers of canon in earlier periods must have engaged in more sophisticated compositional strategies even though these are not immediately clear to us from most surviving theoretical documents. This belief is confirmed by a small number of treatises from the sixteenth and seventeenth centuries that, indeed, provide much more detailed information on how to write a canon. This information relates to voice-leading prescriptions that ensure consonant intervallic relationships among the parts for the duration of the work. Careful study of these sources is worthwhile not only for their valuable information on the history of canon but also because of their potential application in a present-day counterpoint classroom.
Musicological scholarship has had little engagement with these sources for canon,6 although several scholars have recently begun to explore what may be universal laws that govern strict forms of imitative writing, especially in contexts where voice entries occur after short time intervals. Studies in the 1990s by Robert Gauldin, Robert Morris, and Alan Gosman propose abstract algorithmic schemes for writing canons.7 All three studies contain calculations of consonant intervallic patterns formed by the first canonic voice on notes separated by the time distance of the canon, an aspect of their work that has much in common with the voice-leading specifications in the historical sources that provide rules for canonic writing. The work of John Milsom and Julian Grimshaw has focussed on principles of fuga in late fifteenth- and sixteenth-century repertoire.8 Milsom in particular has developed a useful lexicon for imitative procedures in Renaissance music, and his note-against-note reductive analyses of repertoire examples suggest overall that there may be deep underlying laws that govern the construction of strictly controlled imitative counterpoint—laws that come into play whether a composer used them self-consciously or intuitively.
Although they do not situate their work in the historical theoretical sources, the work of modern scholars reinforces my belief that Renaissance composers must have engaged with basic underlying rules when writing different contrapuntal configurations. Inspired by Glenn Gould's playful "So You Want to Write a Fugue?" written for a 1963 CBC-TV program called "The Anatomy of the Fugue,"9 my purpose in this article is to establish principles of two-part canonic writing that may inform pedagogical strategies in a present-day tertiary-level course in modal counterpoint. My discussion will draw upon evidence from the historical theorists and show how it may be usefully complemented by the abstract algorithmical protocols and analytical methods of modern scholarship. I will demonstrate how certain basic procedures drawn from broad principles can be applied successfully by beginning students of canonic counterpoint.
Several scholars have noted the decline of counterpoint classes in tertiary-level curricula.10 Due to limited resources and opportunities for presenting the techniques and contexts of contrapuntal traditions, a counterpoint instructor likely has limited time to allocate to canon. Development of students' skills beyond two-part canonic writing is therefore rare, with few progressing to canons by inversion, retrograde, augmentation or to canons for three or more parts. The method I will present here focuses on two-part canonic imitation in regular motion, which is typically a student's first encounter with the topic and for which a systematic set of guidelines would be useful. I will not consider in detail every canonic possibility from unison to octave above or below, but instead focus on certain cases which can serve as models for writing other types of canon. The final part of my discussion will consider two-part canonic writing in the presence of a cantus firmus, examples of which abound in sixteenth- and seventeenth-century theoretical and practical sources for canon.
Principles derived from historical treatises
In the following discussion I will focus on the detailed voice-leading instructions for canonic writing found in a small number of late sixteenth-century treatises. The most important contributions were by Gioseffo Zarlino (1517-1590) and William Bathe (1564-1614),11 while valuable information about the stages involved in writing a canon can also be derived from treatise examples by Thomas Morley (1558-1603).12 In different ways, these theorists articulated a method for composing canons based on the regulation of the melodic and harmonic intervallic choices of the dux according to the interval of imitation between the dux and comes (I use the terms dux and comes to refer to the opening and following canonic voices respectively.) That they did so in the context of cantus firmus composition attests to the importance of cantus firmus treatment in music education in the sixteenth and seventeenth centuries, and it may indicate the origin of this material in improvised practice.13
Zarlino and Bathe appear to have worked independently of each other, with Zarlino prescribing rules for a small number of canon types, whereas Bathe devised a tabular method for writing canons at all intervals from unison to seventh above or below. Later theorists such as the Nanino brothers (Giovanni Maria (ca. 1543-1607) and Giovanni Bernardino (ca. 1560-1623) and Angelo Berardi (ca.1636-1694) were indebted to Zarlino's work but did not provide additional insight into writing canons.14 Bathe's work has been overlooked and poorly understood to the present day. His contemporary Thomas Morley claimed that "the forme of making the Canons is so manie and diuers waies altered, that no generall rule may be gathered,"15 suggesting that he was unaware of the work of Zarlino of Bathe. Passing references to some specific rules for canonic writing may occasionally be found in other sixteenth- and seventeenth-century sources, often in contexts concerned with non-canonic topics. These will not be considered here as the focus is on theoretical writings that attempted to formulate general principles of canonic writing. All of the surviving discussions for canonic writing deal with only two parts in the presence of a cantus firmus at short time intervals; there is nothing on canonic textures for three or more parts or relatively large temporal distances between the parts.16 Two broad rule classes are evident, one for the regulation of consonance between two canonic parts and the other for the coordination of the canonic parts when a cantus firmus is present. Observance of these rules gives rise to a first species exercise from which a fully worked-out piece in mixed values is derived. These rules are best demonstrated through examples.
The first rule class concerns the melodic motion in the dux so that consonant harmonic intervals are formed between it and the second canonic part, the comes. For example, in a canon at the fifth above after a half note, Zarlino states that the dux melodic line should not proceed by ascending fourths and sixths or by descending thirds and fifths.17 These would lead to dissonant seconds, sevenths or ninths with the comes. For ease of understanding, I illustrate these rules in Example 1.
Example 1: Zarlino, prohibited dux melodic intervals in a canon at the fifth above. 
Zarlino's second rule class takes into account the presence of a cantus firmus. This means that the choice of melodic intervals for the dux is restricted not only by what is to appear in the comes but also by the necessity of maintaining consonant intervals with each melodic progression of the cantus firmus. Example 2 illustrates this rule in relation to cantus firmus progressions by unison and ascending second in a canon at the fifth above. For unison progressions, Zarlino specifies that the dux should form an octave above or third below the cantus firmus on the first note of the latter's melodic interval. For stepwise ascending motion in the cantus firmus, Zarlino allows a third or a fifth between dux and cantus firmus. In this way consonant outcomes are assured when the consequente follows on the second cantus- firmus note.
Example 2: dux-CF progressions in a canon at the fifth above, based on Zarlino's Le istitutioni harmoniche 3rd ed. (1573), p. 308. 
There is one vital aspect to both rule classes: the intervallic calculation is dependent on the time distance of the canon. In both Examples 1 and 2, canonic imitation at a half note is presented, leading to a first- or second-species framework for constructing canons. The creative component of filling in such a texture according to stylistic norms is left unaddressed by theorists (with the exception of Morley, as we shall see below), although the musical examples found in all treatises clearly reflect fully worked-out solutions using mixed values.18
William Bathe's tabular method for writing canons is based upon the same two rule classes as discussed by Zarlino, but the presentation of material is very different. By referring to Bathe's table, a student can find information on the melodic intervals available to the dux and also the harmonic intervals formed by this part according to the melodic motion of the cantus firmus.19 Bathe's table is noteworthy because it attempts to combine the two different rule classes described above into one representational format. Furthermore, it offers a general method for writing any cantus firmus-based canon from unison to seventh above or below according to combinatorial principles. Unfortunately, as with much of Bathe's treatise, idiosyncratic terminology and typographical errors and inconsistencies hinder the reader's comprehension of his tabular method. No musical examples accompany Bathe's brief and cryptic textual commentary on the table. Rather than enter a detailed explanation of Bathe's table here, I refer interested readers to Kevin Karnes's excellent recent critical edition of Bathe's treatise for a full discussion.20 Later in this study, I will show how some aspects of Bathe's tabular presentation may be transformed into useful present-day pedagogical material for teaching cantus firmus-based canons.
Bathe's contemporary, Thomas Morley, made explicit the two stages of composing canons that is implicit in the canonic theories of Zarlino, Bathe and other theorists. Morley provided two versions for some of his musical examples, what he termed "plaine" and "divided." These correspond to a first-species framework and the fully worked-out version respectively. The plain version is a note-against-note demonstration of an overall consonant framework, while the divided version varies the rhythms through repeated notes, passing notes or suspensions.21 In Examples 3a and 3b we see Morley's demonstration of these procedures in a canon at the fourth above after a whole note. Example 3a is a first-species version showing how the canonic voices proceed in consonant intervals at the time distance of the canon. In Example 3b the same notes mostly occur at the onset of each cantus firmus note but the texture is enlivened by repeated notes, passing notes, rests and the "fake" suspension (in mm. 2 and 7).22 The problem of fourths between the two canonic parts in measures 3 and 4 is circumvented because of the presence of the cantus firmus below. Different notes are substituted in the dux at the onset of the second cantus firmus note in measure 3 and the first in measure 4—a subtle manoeuvre that nevertheless maintains consonance with the comes.
Example 3a. Morley, "Plaine" version. A Plaine and Easie Introduction, p. 98. 
Example 3b. Morley, "Divided" version. A Plaine and Easie Introduction, p. 98. 
In summary, the voice leading prescriptions for canonic writing found in late Renaissance sources pertain to either the melodic motion of the dux so that consonant outcomes are assured with the comes or to the consonant harmonic intervals formed between the dux and the first note of a cantus firmus melodic progression so that the comes is consonant with the second cantus firmus note. All theorists calculate intervals in each rule class according to note onsets separated by the temporal distance of the canon. This leads to consonant note-against-note frameworks based on predetermined melodic or intervallic choices for the dux. That the intervening texture is enlivened according to the stylistic norms of Renaissance counterpoint is made explicit in Morley's plain and divided versions of his canonic examples and also by the examples given by Zarlino and other theorists that are all in diminished counterpoint.
A New Method For Teaching Canon In The Modern Theory Class
I now advance a method of teaching canon that draws upon the two rule classes for canonic writing identified in the above discussion of the historical theoretical sources. I focus first on two-part canonic writing at short time intervals and consider cantus firmus-based canon later. I propose the following specific steps for a two-part canon without cantus firmus: decide the canon type (unison, second above, third below, etc.); calculate a list of harmonic intervals that result between dux and comes for each dux melodic progression from unison to octave above or below; exclude cases from this list considered inappropriate on stylistic grounds; write a first species version based on the allowable intervals; expand this to a final version in diminished counterpoint.
By way of demonstration, consider a canon at the fifth above. Example 4 takes each melodic progression of the dux from unison to octave above or below,23 and calculates the resulting harmonic interval with the comes. The purpose here is to arrive at a list of permitted dux melodic intervals according to the first rule class as outlined in the discussion of Zarlino and Bathe above. My thinking about how to accomplish this task has been influenced by the work of Robert Morris, whose investigations of generalized principles for canonic writing includes tabulating permitted melodic intervallic choices for the dux in a first species context.24 For a canon at the fifth above, Morris calculates all possible successions of two intervals, whereas I simplify this procedure in Example 4 so that students identify all single dux melodic intervals leading to consonant outcomes with the comes.
Example 4: Selection of dux intervals in a canon at the fifth above. 
The next step involves excluding cases leading to unwanted dissonance between the two parts or to other breaches of stylistic norms, an issue that Morris also considered.25 Melodic intervals in the dux that bring about harmonic seconds, fourths and sevenths between the two canonic parts are therefore pruned. Other stylistic considerations that may lead to further exclusions include part crossing or an "awkward" melodic interval such as a seventh in the dux. A wide leap such as a seventh may be ameliorated in the final, diminished version of the canon if the time distance of the canon permits sufficient additional notes between dux onsets.26 Part crossing is generally inevitable in a canon at the unison, second or third but an instructor may wish to discourage it in canons at wider intervals of imitation in order to reinforce students' awareness of the independence of parts. Based on Example 4, the list of permitted dux intervals comprises the unison, ascending third, fifth and seventh, descending second, fourth, sixth and octave. Of these, the ascending seventh needs to be treated with particular care because it leads to part crossing and it is an awkward melodic interval normally excluded on stylistic grounds, particularly in a canon at a short time distance, often termed a stretto canon.27
A task such as compiling Example 4 is useful practice for students, although time constraints may preclude repeating the process for other canons, in which case the instructor can provide further information in tabular form for students' use. Table 1 is given with this in mind. It has entries for all permitted dux melodic intervals in canons from unison to octave above or below.28 Resulting harmonic intervals between dux and comes are tabulated; for instance, if the dux proceeds by a descending third in a canon at the fourth above, then the resulting sixth between dux and comes is indicated by the cell at the intersection of column 6 and row 8. Cells are blank if the dux melodic interval leads to a dissonant harmonic interval with the comes. I have retained cases where parts may cross as well as sevenths, as I believe that instructors should discuss these issues with students. Part-crossing is indicated in Table 1 by minus signs placed to the left of numbers in cells.
Table 1 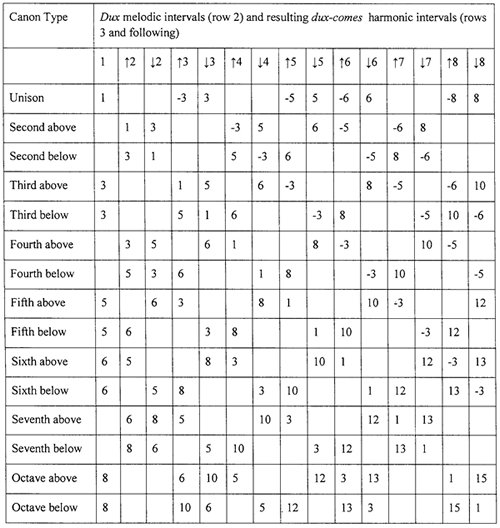
Permitted dux intervals and resulting dux-comes harmonic intervals in canons from unison to octave above and below. Up and down arrows in row 2 refer to ascending and descending dux intervals respectively. Negative signs placed before numbers indicate part crossing.
Returning to Example 4, the next stage involves writing a first species exercise based on the list of permitted intervals for this canon type. I assume that students are aware of rules for good melodic contour and the specific rules of first-species voice leading.29 Therefore, random selection of interval progressions from a list for any canon type is unlikely to generate an acceptable piece. Example 5 reveals potential pitfalls awaiting a student with insufficient preparation in basic areas of modal counterpoint. A troublesome matter arises when certain combinations of permitted dux progressions lead to grammatical errors such as consecutive fifths or octaves. In Example 5, several parallel octaves by similar and contrary motion arise between bars 6 and 9 even though each melodic interval in the dux is drawn from the permitted list of intervals for this canon type. This problem can be solved easily enough by telling students that a dux melodic interval can be used two or more times in succession if its first instance does not lead to a dux-comes harmonic interval of a fifth or octave (or their compound equivalents).
Example 5. Problematic first species attempt. 
The last stage in my proposed method for writing canons involves transforming the first-species version into a final version in diminished counterpoint. Examples 6a and 6b demonstrate this process. Example 6a is an improved version of Example 5, while Example 6b uses mixed rhythmic values, passing tones and suspensions. The creative component of completing Example 6b is guided by the requirement of strict imitation between the parts while maintaining stylistic norms. Therefore, the student should be aware that any proposed change or addition to the dux between the note-against-note and final versions could lead to breaches of stylistic conventions when carried through in the comes. A good general recommendation to students is to keep the texture uncluttered and to expect occasional use of whole notes among the canonic parts in the divided version, as can be seen in Example 3b by Morley above and in other canonic examples by this and other theorists.30
Example 6a: Canon at the fifth above, first species. 
Example 6b. Canon at the fifth above, final version. 
Turning to student instruction in writing cantus firmus_based canons, Zarlino's very detailed voice-leading rules offer a set of useful case studies that can be used in class. The instructor can demonstrate the second rule class with material drawn from Zarlino, such as Example 2 above, but it should also be made clear to students that the dux-comes information in Table 1 needs to be adhered to also. Consider Example 7: when the cantus firmus ascends by second (mm. 2-3), then its first note can only form a harmonic interval of a third or fifth with the dux (a third is chosen in Example 7). Although Zarlino and Bathe both allow a harmonic fifth between dux and cantus firmus when the cantus firmus descends by a second (measures 3-4), care should be taken that the dux does not approach this interval by a prohibited melodic interval. See the error in measure 3 arising from a forbidden melodic fourth in the dux (recall Example 1 above, where the ascending fourth was prohibited by Zarlino in this canon type).
Example 7. Problematic cantus firmus-based canon at the fifth above. 
I believe that cantus firmus-based canonic writing is an integral part of the study of Renaissance counterpoint and is fully deserving of treatment in a modern counterpoint class.31 Therefore, I propose Table 2, which presents only the rules for the dux-cantus firmus relationship across canon types from unison to seventh above or below. In its layout, Table 2 draws upon Bathe's representational scheme, but I exclude information pertaining to the first rule class and I employ modern terminology. I follow Bathe in assuming that the cantus firmus is always the lowest sounding part.32 When writing a two-part canon over a cantus firmus, students should use Table 2 in tandem with Table 1 in order to construct a note-against-note version as the basis for a fully-fledged piece in diminished counterpoint. I recommend that students first identify dux-cantus firmus harmonic intervals according to Table 2 and then refer to Table 1 to ensure correct dux-comes progressions. In this way, the problematic situation encountered in Example 7 may be avoided.
Table 2
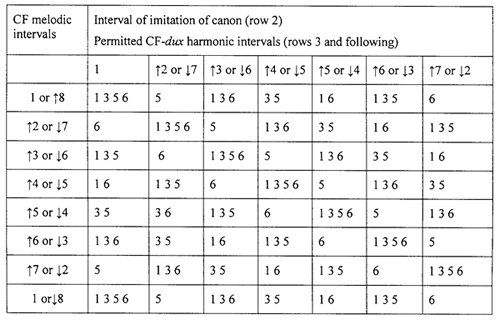
Permitted harmonic intervals formed between dux and cantus firmus
Cantus-firmus canons are considerably more difficult to compose than the two-part canons discussed above. Some practical approaches are worth considering. A useful strategy is to sketch in all of the notes available to the dux over each cantus firmus note according to the possibilities derived from Table 2 and to also write their comes versions. In this way, identifying the range of possible notes at the outset can assist the student in overall planning based not only on good melodic contour but also on excluding dissonant outcomes or parallel perfect intervals. Furthermore, according to Table 2, certain cantus-firmus melodic progressions have two or more possible harmonic intervallic combinations with the dux on the first cantus firmus note, whereas others only have one possible interval. Therefore, it is worthwhile to pay particular attention at the outset to identify any cantus-firmus progression with only one possible intervallic outcome with the dux because the note required in the dux will likely narrow the range of possible preceding and following dux notes. Similarly, the cadence point should be attended to at the outset because there is usually only a very small combination of notes that will lead to a satisfactory cadence, which should be identified and also sketched in. It may not always be possible to write an idiomatic suspension formula at the cadence points because of the restrictions of canonic writing. One further point is that although the historical theorists do not specify whether or not they include compound intervals in their prescriptions for dux-cantus firmus intervals, I recommend their inclusion so that the canonic exercise does not become too constricted.
By way of demonstration, Examples 8 and 9 are two attempts to write canons on a cantus firmus "borrowed" from Peter Schubert's counterpoint text.33 These examples show that a given cantus firmus is not necessarily suitable for canonic writing at any interval from unison to octave. Consider Example 8, a canon at the fifth above: the main problem is that the cantus firmus has many successive descending seconds which are difficult to treat because of the high risk of parallel perfect intervals arising between the canonic parts and the cantus firmus (problems are indicated by square brackets in Example 8). Trying to find alternative dux progressions in this example would lead to yet further voice leading errors or, at best, a very stale melodic line. Note that in this canon type an ascending fourth in the cantus firmus (mm 2-3) must form a fifth with the dux (D_A), the only available interval according to Table 2. This greatly restricts the choices available to the canonic parts in measures 1 and 2. The approach to the cadence is also troublesome: a 7-6 suspension will not work because the dux would need to set up a pattern to be imitated involving its earlier notes G and F, indicated by a square bracket, leading to parallel octaves with the cantus firmus.
Example 8. Canon at the fifth above over a cantus firmus. 
Example 9 is a canon at the fifth below over the same cantus firmus. Note that the series of descending seconds in the cantus firmus become a chain of 6/3 sonorities with the canonic parts. There is no alternative solution because, according to Table 2, a descending second in the cantus firmus requires either a unison or sixth with the dux (and the unison is excluded in order to avoid a chain of parallel perfect intervals). The cantus-firmus ascending third in measures 3-4 can only be treated by a dux note C in measure 3 (according to Table 2). Example 9b uses the fake suspension at the end because a normal 7-6 suspension between the outer parts would not yield a note of the D triad in the comes in the final measure. Other alterations to the texture include suspensions (measures 4 and 5), some passing notes and second species writing.
Examples 9a and 9b. Canon at the fifth below over a cantus firmus. 
Conclusion
The method for two-part canonic writing that I have presented in this study provides an ordered learning process suitable for beginning students of canon. It is not a definitive system for writing canons in general because I restrict my discussion to canons for two parts with or without a cantus firmus at short time intervals, and I consider only imitation in similar motion but not contrary motion or retrograde or any of the other more learned devices often favored amongst enthusiasts of canon. I do not address the complexities of canonic writing for three or more parts because these go beyond what undergraduate students can be reasonably expected to grasp in present-day learning environments, and they are not considered by the historical theorists. Furthermore, I do not take into account difficulties that arise in canons with widely-spaced voice entries. The historical theoretical literature includes many examples of canon at contrasting temporal distances but without any discussion on how to write them.34 Obviously, a first-species approach for canons based on note onsets separated by a wide time interval would be of limited use,35 and it is possible that a different pedagogical method is needed for teaching such canons.
The historically-informed method for teaching canons in the undergraduate theory class presented in this study provides a structured approach based on delimiting the intervallic choices available to the dux, and it enables students to develop skills in long-range compositional planning—something not readily available in the traditional step-by-step approach to writing canon. The method proposed here complements current pedagogical approaches to modal counterpoint in general and should not be undertaken by students without prior instruction in the basic principles. Finally, by linking current pedagogical approaches with historical evidence on how earlier students and composers approached canonic counterpoint, we can gain greater awareness of the inner workings of polyphonic repertoire of the Renaissance period.
Bibliography
Bathe, William. A Briefe Introduction to the Skill of Song. Edited by Kevin C. Karnes. Aldershot: Ashgate, 2005.
Berardi, Angelo. Documenti armonici. Bologna: G. Monti, 1687. Reprint Bologna: Forni, 1970.
Bevin, Elway. A Briefe and Short Instruction of the Art of Musicke. Edited by Denis Collins. Aldershot: Ashgate, 2007.
Bridge, J. Frederick. Double Counterpoint and Canon. London: Novello, 1881.
Collins, Denis. Canon in Music Theory from c. 1550 to c. 1800. Ph.D. diss., Stanford University, 1992.
Collins, Denis. "Zarlino and Berardi as Teachers of Canon." Theoria 7 (1993): 103-23.
Ferand, Ernest T. "Improvised Vocal Counterpoint in the Late Renaissance and Early Baroque." Annales Musicologiques 4 (1956): 129-74.
Gauldin, Robert. A Practical Approach to Sixteenth-Century Counterpoint. New York: Prentice-Hall, 1985.
Gauldin, Robert. A Practical Approach to Eighteenth-Century Counterpoint. New York: Prentice-Hall, 1988.
Gauldin, Robert. "The Composition of Late Renaissance Stretto Canons." Theory and Practice 21 (1997): 29-54.
Goetschius, Percy. Counterpoint Applied in the Invention, Fugue, Canon and Other Polyphonic Works. New York: Schirmer, 1930.
Gosman, Alan. "Stacked Canon and Renaissance Compositional Procedure." Journal of Music Theory 41, no. 2 (1997): 289-317.
Grimshaw, Julian. "Morley's Rule for First-Species Canon." Early Music 34, no. 4 (2006): 661-66.
Grimshaw, Julian. "Sixteenth-Century English Fuga: Sequential and Peak-Note Subjects." Musical Times 148:1900 (2007): 61-78.
Jeppesen, Knud. Counterpoint: The Polyphonic Vocal Style of the Sixteenth Century. Translated by Glen Haydon. New York: Dover, 1992.
Kennan, Kent. Counterpoint. 4th ed. Englewood Cliffs, NJ: Prentice-Hall, 1999.
Lamla, Michael. Kanonkünste im barocken Italien, insbesondere in Rom. Ph.D. diss., Universität des Saarlandes, 2003.
Milsom, John. "Imitatio, 'Intertextuality,' and Early Music." In Citation and Authority in Medieval and Renaissance Musical Culture: Learning from the Learned, edited by S. Clark and E. E. Leach, 141-51. Woodbridge: Boydell Press, 2005.
Milsom, John. "Crecquillon, Clemens, and Four-Voice Fuga." In Beyond Contemporary Fame: Reassessing the Art of Clemens non Papa and Thomas Crecquillon, edited by E. Jas, 293-345. Turnhout, 2005.
Morley, Thomas. APlaine and Easie Introduction to Practicall Musicke. London: Peter Short, 1597.
Morris, Robert D. "The Structure of First-Species Canon in Modal, Tonal and Atonal Musics." Intégral 9 (1995): 33-66.
Nanino, Giovanni Maria and Giovanni Bernardino. Regole di contrappunto di Gio. M. Nanino e del suo fratello minore. Manuscript, Bologna, Civico Museo Bibliografico Musicale.
Owen, Harold. Modal and Tonal Counterpoint from Josquin to Stravinsky. New York: Schirmer, 1992.
Prout, Ebenezer. Double Counterpoint and Canon. 2nd ed. London: Augener, n.d.
Schubert, Peter. Modal Counterpoint, RenaissanceStyle. New York: Oxford University Press, 1999.
Schubert, Peter. "Counterpoint Pedagogy in the Renaissance." In The Cambridge History of Music Theory, edited by Thomas Christensen, 503-33. Cambridge: Cambridge University Press, 2002.
Schubert, Peter. Review of Yearsley, David. Bach and the Meanings of Counterpoint, Music Theory Online 12, no. 1 (2006): 1-15.
Simpson, Christopher. A Compendium of Practicall Musick. 3rd ed. London: H. Brome, 1678.
Smith, Charlotte. A Manual of Sixteenth-Century Contrapuntal Style. Newpark, DE: University of Delaware Press, 1989.
Zarlino, Gioseffo. Le istitutioni harmoniche. 3rd ed. Venice: F. Senese, 1573.
Zarlino, Gioseffo. The Art of Counterpoint. Part III of Le istitutioni harmoniche, 1558. Edited and translated by Guy A. Marco and Claude V. Palisca. New York: Norton, 1968.
Footnotes
1School of Music, The University of Queensland, Brisbane, Australia. An earlier version of this paper was read at the International Conference of the College Music Society in Bangkok, Thailand in July 2007.
2Schubert, "Counterpoint Pedagogy," 503-33.
3See Collins, Canon, 137-38.
4For instance, see Owen, Modal and Tonal, 47-48, 222-23; Schubert, Modal Counterpoint, 147-48; Kennan, Counterpoint, 96-97. This method is also outlined in numerous older texts, a sample of which includes Jeppesen, Counterpoint, 235; Prout, Double Counterpoint, 160-61; Goetschius, Counterpoint, 293; Bridge, Double Counterpoint, 101.
5Such surveys typically include canons by contrary motion, augmentation, diminution, rounds, canons per tonos, augmentation, retrograde and puzzle canons. Although the surveys include modal and tonal canons, there is greater representation of the latter kind. In addition to the texts cited in the previous note, see also Gauldin, Eighteenth-Century, 194-208. Gauldin's Sixteenth-Century, 113-17 deals briefly with some of the complexities involved in three-part canonic writing; otherwise, there is only fleeting reference to two-part canons (p. 53). A few examples of canon can be found in Charlotte Smith, A Manual.
6In an earlier study, I provided a summary of Zarlino's and Berardi's theories but stopped short of detailed discussion of how this material may be applied in a modern theory class. Collins, "Zarlino and Berardi."
7Gauldin, "Late Renaissance"; Morris, "The Structure"; Gosman, "Stacked Canon".
8See Milsom, "Imitatio"; Milsom, "Crequillon"; Grimshaw, "Sixteenth-century".
9Broadcast on March 4, 1963. Glenn Gould Archive, http://www.collectionscanada.ca/glenngould/index-e.html, accessed September 6, 2007.
10Most recently, see Schubert, Review, 14.
11Zarlino, Le istitutioni, 302-317. Some of the examples are included in the first edition, 1558; see Zarlino, The Art, 215-20. Bathe, A Briefe Introduction, 79-80.
12Morley, A Plaine and Easie Introduction.
13A detailed discussion is in Ferand, "Improvised Vocal Counterpoint."
14G. M. and G. B. Nanino, Regole; Berardi, Documenti, 86-132.
15Morley, A Plaine and Easie Introduction, 98. Later in the seventeenth century, Christopher Simpson claimed that "Divers of our Countreymen have been excellent in this kind of Musick: but none (that I meet with) have publish'd any Instructions for making a Canon" (Compendium, 147). Although many English theorists were aware of the 1558 edition of Zarlino's treatise, they may not have been familiar with the revised 1573 edition with its expanded chapter on cantus firmus-based canons.
16Modern scholarship likewise considers only short time distances between voice entries and little on multi-voiced canonic writing.
17Zarlino, Le istitutioni, 308. For a detailed account of Zarlino's rules for canons at this and other intervals see Collins, "Zarlino and Berardi." In the present discussion I draw upon Zarlino's rules for a canon at the fifth above in order to demonstrate how the two rule categories operate.
18The general problem of the "missing link" in historical sources between first species writing and florid counterpoint is addressed by Schubert, "Counterpoint Pedagogy," 517-18.
19Bathe, A Briefe Introduction, 79-80. An electronic facsimile of the Cambridge University Library copy of the treatise may be found at Early English Books Online, http://www.chadwyck.com/home. Bathe's table for composing canons may be viewed as image 17 of this electronic record.
20Bathe, Introduction, 36-44. I may add to Karnes's discussion by noting a typographical error in row 12 of the table for the "obseruations of the places down." The first and second "obseruations" should be corrected to read "1, 7, 6, 5, 4, 3, 2" and "5, 4, 3, 2, 1, 7, 6" respectively. These figures alert the reader to unwanted perfect parallel intervals that arise between the canonic parts when the dux proceeds by ascending melodic intervals specified by these numbers. I provide a full discussion of Bathe's table in a separate study, "William Bathe's Tabular Method and Late Renaissance Theories of Canon Composition" (forthcoming).
21Morley, A Plaine and Easie Introduction, 98-100. Morley offered only two written rules for writing canons that belong to the first rule class as discussed above. In a recent study I suggest that Morley may have derived them from Bathe's table, while Julian Grimshaw sees possible connections to Italian theorists such as Lusitano. See Bevin, A Briefe and Short Instruction, 15; Grimshaw, "Morley's Rule," 665.
22According to Peter Schubert, the "fake" suspension occurs when the dissonance is not prepared properly. See Schubert, Modal Counterpoint, 75.
23Intervals greater than an octave can of course be considered but have not been included here for ease of presentation.
24Morris, "The Structure," 41-47. Morris's study is an attempt to relate the structural practices of serial composition and modal polyphony through a study of first species canons using a methodology that can accommodate modal, tonal and post-tonal concepts. His observations on tonal and pre-tonal canonic structures are most relevant to the present study, in particular his recommendations on how to generate lists of permitted dux melodic intervals according to canon type.
25Morris, "The Structure," 39-41.
26Likewise, intervals greater than an octave in the dux may work in canons at relatively large time distances.
27As for instance, in Gauldin, "The Composition." The work of Gauldin and Gosman lies outside the scope of this part of my study as they deal with algorithmic principles for canonic textures for three or more parts, which is in essence an extension of the first rule class discussed by historical theorists in two-part canonic contexts.
28In its design, Table 1 draws upon the tabular nature of Bathe's canonic method. To find predetermined available intervals, the reader locates cells at the intersection of parameters indicated by column 1 and row 1. Bathe's table, however, includes information for both rule classes (as discussed above), whereas Table 1 pertains only to the first class. Morris generates a similar table (p. 46) but does not include results for when parts cross or for dux melodic seventh intervals.
29For example, see Schubert, Modal Counterpoint, 26-41.
30Another aspect of canonic imitation that an instructor may wish to consider is the maintenance of exact intervallic imitation between the canonic parts so that, for example, a major third is answered by a major third, not a minor third. Even though this issue was considered in the theoretical accounts of canon and is evident in many Renaissance repertoire examples, it would increase the difficulty facing a present-day student of canon and I have therefore not pursued it in this paper.
31The popularity of cantus firmus-based canonic writing in the late Renaissance period is described in Lamla, Kanonkünste, and Bevin, A Briefe and Short Instruction, 23-39.
32It is of course possible to place the cantus firmus in an upper register but this would require a modified version of Table 2, something not provided by any author, historical or modern.
33Schubert, Modal Counterpoint, 33. It also appears in older texts including J.J. Fux's Gradus ad parnassum."
34The same reluctance to deal with canons at wide temporal distances is evident in the studies by Morris, Gauldin and Gosman and also in the work of Milsom who eschews deliberately fuga at wide distances.
35Robert Morris has suggested that two separate canons can be interleaved to produce a canon at a relatively large distance but acknowledges that great care must be taken so that contrapuntal rules are obeyed overall. Morris concedes also that an alternative approach involving generation of charts showing concatenations of allowable sequences of two or more intervals would quickly become too cumbersome for practical use; Morris, "The Structure," 47-48.


