Abstract
Emerging composer Sky Macklay has written a string quartet entitled Many Many Cadences (2014) which inventively combines the basic operations of neo-Riemannian triadic transformations and voice leading (e.g., Parallel (P), Leading-tone (L), Relative (R), SLIDE, etc.). Concomitantly, predominant-dominant-tonic, dominant-tonic, deceptive, and plagal progressions, and expected resolutions of active scale degrees (e.g., the leading tone) in the standard cadential formulae of Many Many Cadences are overwhelming. Macklay’s parsimonious voice leading is a systematic consequence of her transformational operations. In fact, Macklay’s harmonic use of ic1/2 voice-leading parsimony may often implicate a contextually fluid voice mapping involving a dual process of inversion. Appropriating Iannis Xenakis’ kinematic diagrams for this study’s own special, non-mathematical use, I will present Macklay’s return to pre-modern tonal expectations as both a literal return to common-practice tonality as well as a triadic post-tonality. As the first in-depth analysis of any work by Sky Macklay, this detailed study explores the chord-note mapping premise of Macklay’s neo-Riemannianism and its relevance to twenty-first-century musical discourse.
Introduction
Example 1 provides a piano-score reduction of the first six measures of Sky Macklay’s1Macklay (n.d.). Macklay’s website can be accessed here: https://www.skymacklay.com/, while a YouTube video of Many Many Cadences (with score) as performed by the Spektral Quartet (http://spektralquartet.com/) can be accessed here: https://www.youtube.com/watch?v=mrI39Nf7cj4. Many Many Cadences (2014). The perfect authentic, leading tone imperfect authentic cadences, and plagal progressions involving the tonicizations of 13 different triads are confined by framing C+ harmonies in measures 1 and 6 (the roots of triads will be given in capital letters with a + or – symbol to indicate major or minor chord quality, respectively).
Each one of the 15 related melodic fragments in measures 1-6 ends completely resolved within its tonality. The endings on A (violin I) in particular, although Macklay clearly abandons them in their fleeting tonal fields, are actually points of arrival, the letter names of the chordal roots of which spell out the components of the D+ triad; a tonal hearing of textbook cadential formulae in the key of A+ or F♯- will certainly find a G♯ resolving perhaps up to A or a B in the key of D+ descending to A.
Ex. 1. Macklay, Many Many Cadences, measures 1-6. Notice that each dashed slur signifies a distinct key area, and that accidentals apply only to the note they proceed and to immediate repetitions of that note.

The satisfaction of tonal expectations is indubitably part of the music’s aesthetic, yet tonal expectations are certainly not the only voice-leading expectations a listener should bring to this music. I will use the term “voice leading” synonymously with the term “part writing” or what Dmitri Tymoczko formalized as “bijective” voice leadings, implying a fixed number of voices, in this case, three.2Tymoczko (2008a), 1–49.
Macklay's Harmonic Style(s) as an Emergent Property of Voice Leading
A feature of Macklay’s neoconservative postmodern music is often referred to, in some form or other, as the “return to harmony” or the “return to tonality.”3Bernard (1995), 284. The validity of this appellation is immediately recognized by skimming through the score of Many Many Cadences which, while incorporating glissandi or, rather, portamenti into most of its melodic motions (29 out of the 39 pages of the score call for these microtonal elements), is saturated with common-practice formulaic chord progressions or the use of triads in other ways. However, in the context of Many Many Cadences, this “return” may be better understood as an “assimilation,” which results in a very concentrated presentation of tonal cadential progressions projected along a certain motivic pathway of which Example 1 is paradigmatic.
Ex. 2. Macklay, Many Many Cadences, measures 7-13, progression of roots of tonicized triads.
For the purposes of this study, I will define a harmonic progression as an ordered succession of single triadic sonorities involving idealized voice leadings between the I/i chords of each key area (as established by a cadential formula), meaning that triadic progressions so defined are represented by their most efficient one-to-one voice leading.4Tymoczko (2008a), 1-49. Sometimes they project a process involving interval cycles, although without strictly preserving clockwise motion around the cycle. Example 2, which provides the roots of the tonicized chords for the section in Many Many Cadences that immediately follows the music of Example 1, displays one application of this procedure: the first four-root sequence C-E♭-A-D first accrues to C-E♭-A-D-G-E-C♯-B♭ in measures 7-9 and then, if one substitutes F♯ as the third active scale degree of the fourth key area of D+ of the first four-root sequence, immediately accrues to all three diminished-seventh chords of the three C3-cycles of [C-E♭-A-(F♯)]-[G-E-C♯-B♭]-[D-B-A♭-F]... (The brackets below Example 2 concern this accretion in that they show a progression of the roots of tonicized triads through a motivic pathway that ignores adjacency of pitch-class intervals of the C3-cycles.)
Given this definition of a harmonic progression, one can see that, with the help of transposition, pc diversity is easy to come by when one starts on any pc (considered here as a temporary tonal center) and moves contiguously by any given generating pc interval. With the exception of the C1 and C5 cycles, transposing an interval cycle allows for further avoidance of interior repetitions: starting on C, C30 gives C, E♭, F♯, A, C31 gives C♯, E, G, B♭, and C32 completes the aggregate with D, F, A♭, B.
Ex. 3. Macklay, Many Many Cadences, measures 25-28.

Theorist Scott Murphy’s assessment of Penderecki’s overall melodic practice could be applicable to Macklay’s overall harmonic practice: “This is not unlike an acknowledgment of certain liberties some serial composers take with their realizations of a row.”5Murphy (2007), 217, n. 1. It is as though the fleeting centrically functioning pcs of her harmonies considered linearly are based on a freely atonal scale model. The movement of the harmony in measures 2-6 of Many Many Cadences (Example 1) offers a good example of this diversity: no pc (as root) is repeated in its 11 tonicized triads. The roots of the tonicized triads in the chord progression of Example 2 have pc repetitions, but they are considerably spread out, as demonstrated by the analysis above the music. Each horizontal line represents a non-duplicative pc succession that begins and ends with the two pcs at the line’s two ends. These two series constitute a set of non-duplicative, tonicized root successions in which neither member of the set is completely embedded within the other: their average length is 9.5.6Tenney (1977), 36-69, n. 1. Example 3 providesa similar analysis for a line of tonicized triad roots from later in the quartet (from m. 25): the average length of the two successions is 7. This pc diversity that characterizes Macklay’s overall harmonic practice involves non-duplicative successions of tonal centers from approximately 7 to 10 notes which serve as essentially freely atonal melodic lines. There are 12 members of set-class (037) embedded in the linear succession of the tonicized triadic roots, and, vertically, all the triads themselves are members of the same set-class.
Example 4 shows a representative harmonic progression from a passage involving two complete musical textures occurring at the same time from Many Many Cadences (2014). While the predominant-dominant-tonic, dominant-tonic, deceptive cadences, and plagal progressions continue above, the harmonic progression shown in Example 4a is occurring underneath. Although there are seven non-duplicative successions of chordal roots among the sequences that make up this layer of the passage, all but one non-duplicative succession falls short of the approximate minimum of seven pcs. This type of writing takes Macklay farther away from European and closer to American modernism: Ruggles’s sacrifice of pc nonrepetition for the sake of motivic repetition has been discussed, 7Slottow (2009), 25. Ruggles’ application of pitch-class nonrepetition is very similar to its application in Macklay (2014). As in Ruggles’ melodies, one cannot assign a non-duplicative pc-root succession to every chord in a Macklay fundamental bass; the flexibility of the actual length of these successions is measured as the average number of non-duplicating pc-roots that lead up to and include the pc. Although this is a sound method for computing a general figure for the number of intervening notes one might expect to find in a composer’s motivic pathways, it slightly undervalues those instances in which that number fluctuates wildly from the norm to a greater or lesser extent, which is more in accordance with the present interest (which was often Ruggles’ own) in persistent motivic repetition. and a very rapid, quasi-atonal change of key implication has been noted in Ives’ music.8Cowell (1974): “Ives’s melodies often change key implication very rapidly so that in spots they may suggest atonality. Usually, however, they are plainly major, minor or chromatic; rarely are they modal or genuinely atonal.” (164) Likewise, Macklay’s highly accelerated harmonic rhythm in Many Many Cadences may be teased from the application of the Ivesian principle because it underlies Macklay’s harmonic practice, involving as it does a wide variety of pc-roots as simultaneously avowing and disavowing tonal expectations. The image of “total chromatic saturation”9Searby (2001), n. 216: “... Ligeti completed his Horn Trio - which uses traditional ternary form, a passacaglia (although a disguised one), a strong melodic focus, and a harmonic language which contains clear triads and dominant sevenths in abundance. In spite of his assertions above, it does seem as if Ligeti, in addition to rejecting the Avant-garde, is looking to the past for major elements of his musical language. However, in so doing he avoids the imitation of stylistic features of past music, so prevalent in neo-Romantics such as David Del Tredici and George Rochberg. Ligeti clearly detests such an approach.” (17) that Mike Searby uses to describe Ligeti’s “textural” music of the late 1950s and early 1960s also serves as a metaphor for the pc diversity of Macklay’s “basse fondamentale”10Rameau (1722/1971): “The essence of composition, for harmony as well as melody, lies principally, especially at present, in that bass we call fundamental.” (206): the composer’s priority to aspire toward the inclusion of the pitch-class aggregate by soaking the musical space, both vertically and horizontally.11Pitch class A is included in some vertical sonorities, but not in the root progression itself.
Notice that the four roots of the harmonies of each sequence in Example 4a are usually either members of set-class (016) or consist in whole or in part of (016) subsets, and that a certain normal form transposition of (016) is arranged symmetrically around the [0,1,6] subset of the third sequence [e,0,1,6]. Starting locally with [e,0,1,6] or rather [B,C,D♭,F♯], B and D♭ surround C symmetrically and wedge toward it. More globally, a member of set-class (016) with normal form [E,F,B♭] surround the third sequence, which contains three members of sc(016) ([C,D♭,F♯], [C,F,F♯], and [F♯,B,C]) whose first notes 0 (C) and 6 (F♯) are a tritone apart – the poles of the 0-6 inversional axis (sum 0) – creating a palindrome [C,E,F,F♯,B♭]. These poles together with [E,F,B♭] also constitute the normal form pitch set [4,5,6,t,0], subsets of which are [0,5,6] and [4,5,t] that are not only members of set-class (016), but begin with the notes C and E, respectively. In prime form, [4,5,6,t,0] is set-class (01268), the (016) subsets of which are pitch sets [0,1,6] and [8,1,2]. The first integer name of the latter, together with the C and E of the normal form pitch set, come very close to spelling the C+ triad. This gives measures 46-88 a high degree of self-similarity across scale: The note G, the 5th active scale degree or dominant in the key of C, is repeated in the first sequence, and is given further centricity as the dominant of C by virtue of its upper leading-tone A♭ (integer name 8).
Ex. 4. Macklay, Many Many Cadences, measures 46-88, harmonic progression showing both non-duplicative successions of chordal roots as well as simultaneous symmetrical and functional arrangement of triadic harmony around C and F♯ as the poles of axis 0-6 and the first and last pitches, respectively, of normal form pitch sets [0,1,6], [0,5,6], and [6,e,0].
Ex. 4a. Measures 46-88, lower textural layer.

Likewise, B is repeated in the second sequence, and, as a lower leading tone, gives further local centricity to C. The arrival at the C+ triad at measure 96 (the beginning of the B section of this quartet’s ternary form) resolves the harmonic major third on B (beginning in measure 46) and the two build-ups to a B+maj.7 chord in measures 54-57 and measure 60, respectively, as though these harmonies had served a prolongational leading-tone function. And knowing that the 12 inversional axes are analogous to the 12 major/minor keys of traditional tonality, Example 4b features yet another motivic structure that consists of all but one (A) of the 12 notes (as pc roots) of the chromatic scale that is not only symmetrical around both poles of the 0-6 inversional axis (which are adjacent to each other in measure 74), but is quite literally an incarnation of that axis. All this suggests that C+ is the tonic, but its tonicity is created by both inversional symmetry as well as traditional harmonic functions simultaneously.
Ex. 4b. Measures 46-88, composing-out of inversional axis.
Along with the motivic projection of pc centers, the other feature that characterizes Macklay’s harmony is triadic transformation via voice-leading parsimony (the most efficient) and contextual inversion. Musicians usually “find maximally efficient voice leadings with relative ease,”12Tymoczko (2008a), 49. and one does not need Roman numeral analysis to understand how harmonic successions of triads of different quality would likely show the more or less equidistribution of neo-Riemannian triadic transformations (i.e., Parallel (P), Leading-tone (L), Relative (R), as well as the secondary operations that combine these three) between adjacent chords. The only possible bias might be in the reduced number of SLIDE transformations in common-practice chord progressions, since this transformation involves parallel fifths and so binds together tonally distant chords.13Lewin (2002), n. 2, 196-230. Throughout her string quartet, most triadic transformations weight the minor second and (somewhat less so) the major second considerably more than the minor third and (much less so) any remaining interval class. The non-duplicative successions of chordal roots in Example 4 from Many Many Cadences display intervallic voice-leading preferences very typical of Macklay’s triadic transformations: her triadic harmonies gravitate toward parsimonious voice-leading transformations involving the semitone and the major second interval classes, or what Julian Hook refers to as uniform triadic transformations or UTTs.14Hook (2007), 15.
Theorists John Roeder and Scott Alexander Cook also hear such triadic transformations as a hallmark of the music of contemporary British composer Gavin Bryars (1943- ), beginning with his String Quartet No. 2:
This music appears promising for a neo-Riemannian analysis because, although it is consistently triadic, it lacks fifth progressions, and because the chords always connect parsimoniously.
Furthermore, they note “chord-sequences that are developed” within certain sections of Bryars’ music “demonstrate voice leading that is exclusively parsimonious.” And finally, they say of their analysis that it “demonstrates that Bryars’ harmonies are not to be dismissed simply as non-functional sonorities.” Instead, “the parsimonious voice leading apparent in the music is a systematic, not arbitrary, consequence of the transformational system Bryars employs.”15Roeder and Cook (2006), 46, 55, 66. In a manner similar to Bryars’, Macklay’s string quartet inhabits this neo-Riemannian territory not only in its triadicism but also in its focus on two voice-leading intervals, the semitone and major second. The excerpts from Many Many Cadences discussed thus far exemplify this practice: if one were to connect the pc-center triads of the first three examples, Example 1 would be found to intersperse three minor thirds in voice leading that otherwise uses semitones and major seconds exclusively, Example 2 would be found to intersperse a single minor third, while the voice leading of Example 3 would be found to make exclusive use of semitones and major seconds.
Although Tymoczko defines triadic transformations (e.g., neo-Riemannian transformations) as a strictly harmonic phenomenon that “does not specify any particular mapping between its notes,”16Tymoczko (2008a), 10. Richard Cohn explains that these transformations invert a triad, “mapping major and minor triads to each other,” and that
because the inversional axis is defined in relation to the triad’s component pitch classes, rather than as a fixed point in pitch-class space, this class of transformations is now referred by the term “contextual inversion.”17Cohn (1998), n. 2, 170.
The present study asserts that Macklay’s use of this class of triadic transformation is often equivalent to a contextually fluid voice mapping that can be described as a dual process of inversion. Works such as Many Many Cadences include harmonic passages analyzable according to a form of contextual inversion in which relations by pitch-class inversion are camouflaged by “assumed” transformations that do not actually appear in the passage(s).
Ex. 5. Macklay, Many Many Cadences, six measures before section A1, and theoretical abstraction.

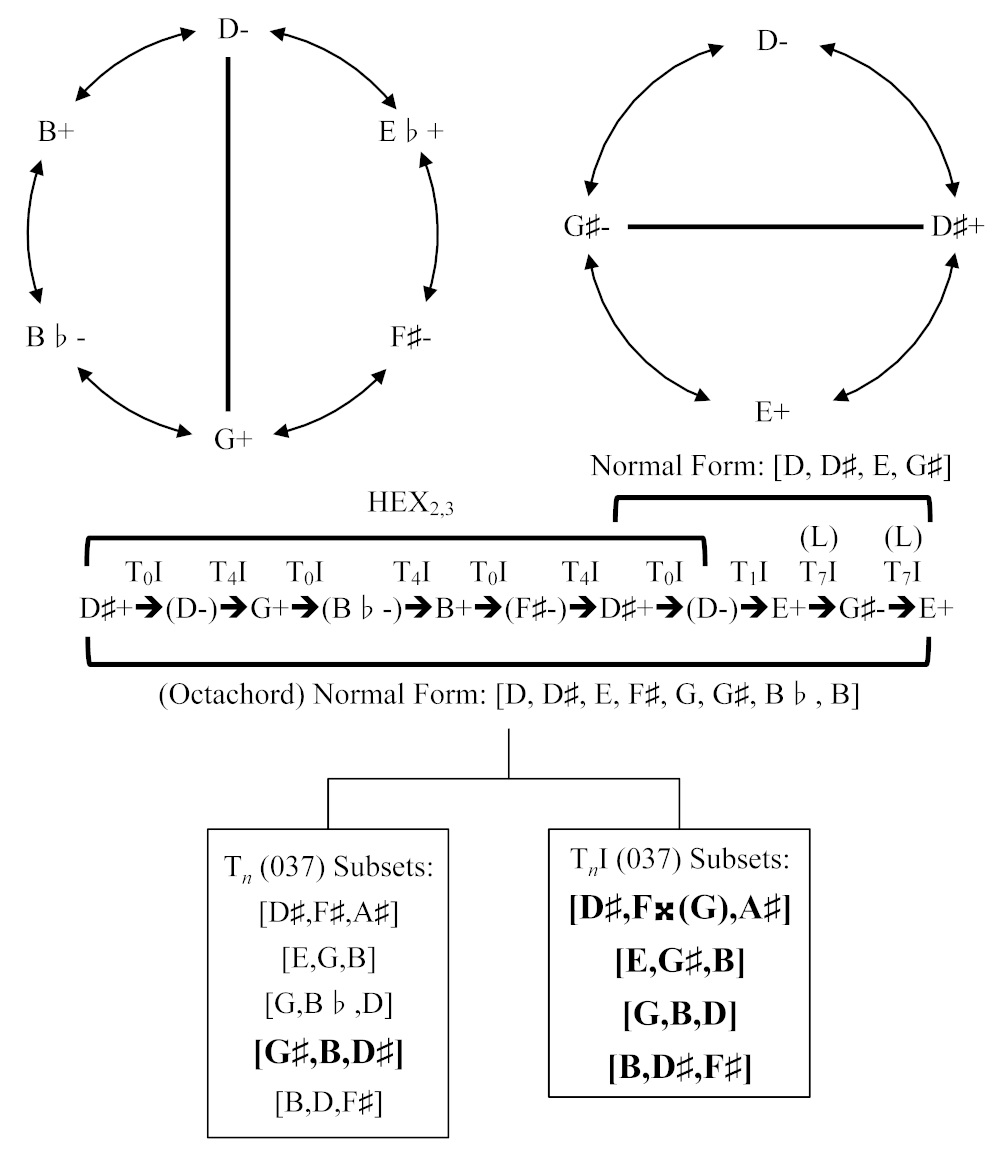
For the most part, the succession of triads in the last six measures of the B section can be interpreted as the result of transposition-cum-parsimonious voice leading and vice versa, but I have expanded it through a process of double inversion into a larger progression. Thus, Example 5 illustrates one important abstract possibility. Beginning with D♯+ and moving by T0I and T4I in alternation, one arrives at a cycle of six triads: major and minor triads built on D♯, D, G, B♭, B, and F♯. Moving through the cycle involves voice leading by no more than two semitones, so that it conforms to ic1/2 parsimony (i.e., each triad differs from its adjacent triads by semitonal and whole-tonal movement of voices). When this cycle (hexatonic collection HEX2,3) is written out as alternating 1s and 3s, the triads of the hexatonic poles (like D- and G+) seem to bear a minor dominant/tonic relationship to each other and together comprise set class (02469).18Gollin (2011), 388. It is interesting to note that, in a discussion of the possibility of a dual-process, contextual-fluid, inversional triadic transformation, sc(02469) is found in a taxonomic list of Riemann’s doppelklänge (double sounds) as a pentachordal set that has been generated by the triadic combination of a major chord and its minor dominant (e.g., D+ and A-).
After arriving back at D♯+, a different double inversional cycle, moving by T0I and T1I, seems to begin, but this is instantly interrupted by an L transformation that is immediately reversed. Except for the progression from D- to E+ which (in parsimonious terms) involves one voice moving by a minor 3rd, each triad in this final succession differs from its neighbors by voice leading consisting of movement by 1s and 2s. If one presents this chord progression in normal form as a cycle, two of the triads lying opposite each other (D♯+ and G♯-) seem to bear a dominant/tonic relationship.19Ibid., 388. Again, it seems quite a coincidence, especially in the present twofold operational context, to come across another binary combination of triads which together generate a pentachordal set (in this case, sc(01348)) that, like sc(02469), is equivalent to one of Riemann’s doppelklänge (double sounds; e.g., A♭+ and D♭-).
Sky Macklay, if she is using a double inversional process (often contextual in the sense of inverting around pitch class components shared between both “assumed” and/or “non-assumed” adjacent chords) to connect triads of the same quality in Many Many Cadences, then perhaps evidence may be found in the expanded fundamental bass of the entire passage considered as the octachord [2,3,4,6,7,8,t,e]. This octachord contains nine subsets belonging to the triad set class (037), five of which are the very triads which actually appear in the score in measures 130-6, and so along with the remaining parallel-minor versions of the four major-quality chords of this passage, produces what looks like evidence that a process of double inversional triadic transformation is taking place.
Kinematic Analysis
Wilfred Meller’s examination of the avant-garde in America begins as follows:
In a sense, avant-garde music is a rear-, not an advance-guard action, for it is both a consequence of, and a reaction against, five hundred years of European ‘consciousness’. The Renaissance started with man’s dualistic awareness of the distinction between the Self and the Non-Self: which in musical terms became the dualistic, and peculiarly European, phenomenon of harmony.20Mellers, (1963 - 1964), 1. For example, in music that has this post-1945 tendency to include a type of experimentalism (still alive today) that is characterized by the rejection of tonality, it generally falls into circumscribed areas of Eurocentric, chauvinistic, and genre-specific analysis, in spite of the growing “rearguard” return to tonality mentioned earlier as a mark of neoconservative postmodernism. Many Many Cadences is undoubtedly both a consequence of, and a paradoxical hybridization of viewpoints, a consequence of both 500 years of the Cartesian dualism that distinguishes between mind and body (or between mind and world), and a nondualistic dissolution of the Kantian categorical distinction between, for instance, “me” and “not-me.” The Renaissance, as a period of cultural advancement in contrast to the Middle Ages, has been called into question. The 14th–17th centuries, seen by some as a period of pessimism and nostalgia for classical antiquity, may be compared to the peculiarly 21st-century American phenomenon marked by a “nostalgia” for the triadic harmonic language of roughly the time from 1600 to 1900. Nondualistically considered, contemporary American culture still has ambitions of advancement while at the same time looking to the past for some overlooked or forgotten means of satisfying that ambition.
With this in mind, Example 6a lays out the roots of the major- and minor-key areas of Macklay’s American harmonic “consciousness” in the opening of Many Many Cadences (Example 1): C+E♭+A+E♭-G+E+D♭+B♭-D+B+A♭+F+E♭+F♯-C+. The alphanumeric designation with superscript above each triad letter name is the C3-interval cycle to which the pc root belongs. The kinematic or transition diagram in which each term is connected to its transform by an arrow is a general, graphical expression of triadic connectivity, regardless of transformation type.21Thus, the kinematic diagrams of this paper concern themselves purely with motion and not with what causes that motion. This is basic to the very definition of kinematics: the study of motion without regard to its cause. The . and we turn our attention not to confuse kinematics with ced.en removed..the ,"textTherefore, one must be careful not to confuse kinematics with kinetics: the study of motion as caused by forces and moments. After the first state of the graph beginning with C, the harmonic progression entertains three potential continuations (according to the kinematic diagram) for its second tonicized root: E♭ could continue to F♯, A, or G, F♯ could continue back to C, A could continue to toggle between itself and E♭, and G could continue around both C31 and C32 until arriving back at E♭. However, when the tonicized root movement goes to A before executing the switchback to E♭, the ground covered so far greatly decreases the possibility that the same tritone leap will follow the E♭, as this would duplicate yet another pc already used. The progression therefore is left with two pc continuations from the E♭ to the F♯, or from the E♭ to the G, “locking” it either way into a journey through all three C3-interval cycles and exhausting the aggregate. However, when the progression arrives at and finishes with C, the circuit is set to start all over again. The sequence from three continuations near the beginning, down to two at the first tonicized E♭ root, then back up to three as implied by the circuitry is in a one-to-one correspondence with the transition from C30 to [C31-C32] back to C30. One might just as well draw an identity of essence between this and the minimal Schenkerian Ursatz I-V-I.
Recalling the quote above, and taking care to notice the harmonized “fundamental bass” with mostly minor-quality triads in measures 7-13 – C-E♭-A-D+G+E-C♯-B♭-D-B-A♭-F-E♭-A-C-, Mellers might have looked upon this as evidence that “the American retreat from the West has been more empirically spontaneous.”22Mellers, (1963 - 1964), 2. This harmonic sequence is analyzed in Example 6b. The remarkable claim made by Mellers that the American avant-garde is derived from experience, particularly from sensory observation, and not derived from the application of logic may explain the omission of an F♯ triad from this progression, eliminating it from the upper circuit of the kinematic graph, although without affecting the “resolution” to the final “I” of the “I-V-I” progression, belying the F♯ triad's “function” as an analogue to mediant/submediant harmony: there is a continuation, from Example 6a, that might reasonably be expected in Example 6b, yet, insofar as the progression concludes with a three-note segment of C30, it ends just as the last one did. Furthermore, not only is F♯ surreptitiously given as an individual pc component of the D+ triad, the respective triad-quality preponderance of three consecutive harmonic statements - the template in measures 1-6, its minor-quality version in measures 7-13, and its restatement (with the exception of the substitution of G- for F+ in measure 17, G being the dominant of C which belongs to the C30 interval cycle) in measures 14-19, may be thought of as an abstraction of the “I-V-I” progression of the initial template on a larger scale.
Ex. 6. Kinematic analysis of the first 19 measures of Many Many Cadences.
Ex. 6a. Measures 1-6.
Ex. 6b. Measures 7-13.
Ex. 6c. Measures 14-9.
Ex. 7. Many Many Cadences, measures 25-9.

Ex. 8. Kinematic analysis of Many Many Cadences, measures 25-9.
Therefore, the C triads are forced into a tonally determinate role regarding the Western expectations generated from a “book-end” perspective as discussed earlier, but they offer the same effect regarding expectations generated by the combination of Macklay’s two idiosyncratic harmonic features. The three C-centered statements give way to an abridged statement that begins by tonicizing B+ and continuing with a rhythmic acceleration culminating with the appearance of a 16th-note quintuplet in measure 28, followed by a return to the C centricity of the first 24 measures, replete with non-tuplet 16th notes as the smallest rhythmic value. Example 7 displays this music that brings respite from the erstwhile C centricity. The two non-duplicative successions that are not completely imbedded in each other are a line of ten notes and a line of five notes that descends by semitone with an upper leading tone back to C, forming with the initial B of the first non-duplicative succession a large-scale statement of sc(012) that serves as a contracting wedge converging on the axis note C. Actually, the two lines together form a larger contracting wedge whose inversional symmetry begins with the minor third above and below C: the tritone between E♭ (to the right of the C+ chord at the midpoint of the progression) and A (to the left of the C+ midpoint). Moving outward from center, there are the pcs a perfect fifth above and below C as well as pcs a major second above and below C: the minor seventh between G on the right and F on the left, and the major third between B♭ on the right and D on the left. At the endpoints there are the minor seconds above and below C: the major second between D♭ (enharmonic C♯) and B, which resolve to C in the next measure. This subliminal inversionally symmetrical contracting wedge converges on the axis note C, and so has a strong centripetal force. As shown in Example 8, all pitches (except for A♭) leading to C from both sides of the diagram are both members of sc(0258); likewise, the inclusion of C in either of these members of sc(0258) results in a member of sc(02358) and so further evinces the use of an inversional axis. Thus, the fusion of pc-center motivic and triadic transformative practice provides an environment that fosters the anticipation of C at the end of this harmonic progression, the balancing of notes against other notes around C, because both triadic transformative harmonic practice as well as pc-center motivic projection embrace both determinism and chaos, undermining while at the same time permitting hierarchical systematization: if there is no hierarchy, then any hierarchy may be imposed, in this case, the use of an inversional axis.
A return to Example 4 provides an example of a succession of triadic simultaneities in the quartet that has no readily discernable compositional scheme. In this saturational root progression, all but one of the twelve tones (as roots of tertian harmonies), presented in order of appearance B F E B♭ G A♭ D♭ C F♯ D♯ D,
Ex. 9. Kinematic analysis of Many Many Cadences, measures 46 – 88.
make up a harmonic texture below the faster texture made up of the ongoing cadential formulae. As shown in Example 9, this 11-note line nearly exhausts the aggregate. The A that one might expect to end this succession is made very mysterious by its omission. Or, to put it another way, the first six pc roots – [B,F,E,B♭,G,A♭] belongs to the set class whose Forte name is 6-z13, while the last six pc roots (if they included A) – [D♭,C,F♯,D♯,D,A] – belongs to the set class whose Forte name is 6-z42, the zygotic mate of 6-z13. To complete this Z-relation in the excerpt of Example 4, Macklay could have placed A anywhere in the progression without violating either ic1/2 voice-leading parsimony or dual-process, contextual-fluid inversion, while continuing a strict observance of pc-center motivic projection by completing a saturational presentation of the aggregate.
Ex. 10. Macklay, Many Many Cadences, measure 108 (B section)

Yet later in the quartet, Macklay brings back a tetrachordal member of a subset of this material (the 11-note root progression is made up of no less than 16 subsets of sc(0136)) for what is arguably the express purpose of comprising A. The quartet boasts five statements of the progression C+, A-, F♯0, B+ (the roots of which constitute a member of sc(0136) at a transposition which includes A) in the middle section of its ternary form, of which the first (measure 108) is shown in Example 10. She begins with sc(0136), but instead of using any of the (0136) subsets that could have been culled from the 11-note collection from measures 46-88, she uses a transposition of sc(0136) that includes A (as well as C with which each of the five statements of the untransposed set class begins). The slower tempo and portamento texture may afford an opportunity for an expert listener to anticipate an extra contrast, especially when remembering that A was omitted from the passage from Example 9 and from the chord progressions in measures 89-95, and recognizing that this is arguably the reason the A- triad is included in every triadically-harmonized, tetrachordal root progression (sc(0136) or otherwise) throughout the B section until measure 129.
Another example of a root progression that coincides with a conclusion articulated by the repetition of one or more pcs (E and its leading tone D♯, in this case) is the excerpt from Many Many Cadences introduced earlier (Example 5). Example 11 provides an analysis in which both motivic design and triadic transformative process can be seen in measures 130-6 (i.e., after the last repetition of the sc(0136) root-movement harmonization) as a rather concentrated composing-out and tonicization of the E+ triad, involving a progression of mostly major quality chords, and signaling the end of the B section. However, the analytical subject need not be the double-inversional eight-note line of both “real” and “assumed” chords, but merely the five that appear in the score, since the roots of the lower part of the diagram spell out B aug. or, rather, the dominant of E+ which then toggles between itself and G♯- – E, G♯, and B – all three components (as roots of triads) of E+ (being the dominant of A- which has been present in every set of four chords since the beginning of this section).
Ex. 11. Kinematic analysis of example 5.
Ex. 11a. Eight-note line of both “real” and “assumed” chords.
Ex. 11b. Five-note line of chords that actually appear in score.
The Macklay Kinematic and a Tabular Survey of the Entire Quartet
The above examples provide instances of communal stationary states among the harmonic progressions, but not in the sense that it is impossible to leave these states, rather, in the sense that the state space is finite even when the features of pc-center motivic projection and ic1/2 voice-leading parsimony and dual-process, contextual-fluid inversion are considered in tandem. But is this state space nonetheless “permeable”23Ligeti (1965), 5-19. In this essay, Ligeti introduced the concept of musical “permeability” according to which a musical structure is “permeable” if it allows a free choice of intervals. The word is used here in a similar fashion to refer to a musical state which allows for free choice of successive triads. Thus, in the same way that Ligeti saw permeability in serial music as a substitute for the form-shaping function of melodic lines, motifs, and harmonies in older styles, the present author sees permeability in Macklay’s triadic post-tonality as equivalent to the form-shaping function of serialism. by the emergence of all possible harmonic progressions? The process of answering this question can begin by enumerating the set of specific triads along with every triad with which it forms a two-chord succession that employs voice leading of mostly unordered pc intervals 1 and 2: what I call Macklay progressions that form the Macklay set. The Macklay set is partitioned into harmonic classes equivalent under the canonic operations of transposition and inversion. A compression of any of the kinematic graphs in the analyses of Examples 6, 8, 9, or 11 (and indeed the Macklay set itself) would result in a transition diagram isomorphic to Example 12, the Macklay kinematic. As in the kinematic graphs of earlier analyses, the arrows connect terms to their transforms (i.e., triads signified by ϒ or gamma, the third letter of the Greek alphabet), therefore representing parsimonious triadic transformations, and epitomizing every possible progression. Like Tymoczko’s systems, the terms of the Macklay kinematic represent particular chords (e.g., “C +”), and not just chord types (e.g., “major triad”).24Tymoczko (2008), 1–49. However, the three arrows that radiate from the kinematic’s “tonal center” – the topmost term – map onto a Macklay harmonic class. Therefore, the Macklay kinematic is also representative of the harmonic classes, because the three arrows in the diagram represent the transformational means by which the content of each class is generated.
As a theorist who has described general principles and procedures for formalizing the notion of voice leading, Tymoczko “shows how to classify voice leadings according to transpositional and inversional equivalence and supplies algorithms for identifying maximally efficient voice leadings between arbitrarily chosen chords.” However, the details of his algorithms for solving this problem are exceedingly technical.25Ibid Ironically, transpositional and inversional equivalence allows for the comparative simplicity of the Macklay kinematic. First, the root (R) and quality (Q) of the initial term could be chosen arbitrarily. Second, the arrows of the graph assume such parsimony that <1> voice leading is equated with its inversion, namely, <e> voice leading or, as Tymoczko puts it, “they do not...distinguish one-semitone ascending motion from eleven-semitone descending motion.”26Tymoczko (2010), 42.
Ex. 12. The Macklay kinematic.
To save space, the kinematic diagram of the entire string quartet has been distilled into the formula of Example 12, in which s stands for “same” and d stands for “different.”
This kinematic proposes a method for describing triadic harmonic content directly from triadic transformations, abstractly considered. The output, which is a function of voice leading (“bijective” part writing) instead of Julian Hook’s algebraic structures, for example, symbolically represents all possible sequences of major and minor triads that extend the triadic character of the initial term. While it is clear that I am reducing the harmony of triadic music to a mere succession of major- and minor-quality triads, as this choice of lexicon assumes, I believe this is a sound basis for an abstract approach to labeling. In other words, the lexicon, and therefore the Mackay kinematic itself, is a robust representation of the semantics of many types of triadic music.
Among all harmonic classes (consisting of a specific chord followed by all the chords to which it goes over the course of Many Many Cadences), there seems to be a strong correlation between Macklay’s aspiration of attaining 12-pc diversity and the record of observing that the largest class has only 10 pc roots. These harmonic classes are tabulated in the Appendix. Following Allen Forte’s nomenclature for unordered set classes, each harmonic class is assigned a two-number label (abbreviated HC in the Appendix) and a prime form (PF) in the two leftmost columns.27Morris (1983/1984), 187-217. Transposing and/or inverting the tonicized roots of a chord progression so that it begins with 0 and is most packed to the left is to put it in “prime form.” For example, C-E♭-C+B+D♭+E♭+ is a member of class 4-2 with a prime form of (0124). This harmonic class can be graphed kinematically according to the Macklay kinematic: as one traces the pitches of the prime form through the graph, the number of arrows (i.e., transformations) from term to term in the progressions represent the number of times the first chord goes to another chord of root d and quality s or d (e.g., the arrow of the harmonic progression from C- to E♭+ is the same as ϒ(R,Q)→ ϒ(Rd,Qd). In the next column of the table, each prime form is characterized by the unordered pc intervals required for parsimonious transformational voice leading, borrowed from what Robert Morris calls INT1, modified to PINT.28Morris (1987), 107. (Incidentally, the triads in bold in the first column are those which required one voice from the initial chord to move by three semitones. I have underlined the quality of the initial chord responsible for voice leading by a 3 in cases involving classes whose first triads have two major- or two minor-triad qualities.)
Although the Macklay kinematic is structurally redundant, this is overshadowed by the diagram’s symmetric yet reiterative complexity, a testament to the union of the two harmonic features of pc-center motivic projection and ic1/2 voice-leading parsimony and dual-process, contextual-fluid inversion. The Appendix column entitled “ϒ/HC” displays the number of triads not included in a harmonic class. It is of analytical interest that, among these harmonic classes, the most saturational harmonic class – 10-1 – is the most rare, occurring on the table only once. Most of these near-saturational harmonic classes end with harmonic class 3-2; this can be seen by finding 3-2’s interval series of <12> at the end of each of their interval series. This promotes 3-2 to a special status among the harmonic classes, not unlike the singular status tonic harmony has among the seven diatonic Stufen. The progressions of tonicized roots in sections A and A1, which terminate at the end of a contour descent and a return to a C triad of major or minor quality, contain high concentrations of 3-2.
Regardless of how many triads of different roots the model generates, there still seems to be a binary distinction between those triads that are expected by ordered means of some generating pc interval and those that are less obviously the result of inversional symmetry, a referential collection (due perhaps to multi-collectional resemblances), or a cyclic set. One could dedifferentiate these two groups by, for example, claiming that triads generated by either pc-center motivic or triadic transformative practice are to be as expected as those generated by the forms of centricity just listed. In the case of the previously discussed incipit of C+E♭+A+E♭-G+E+D♭+B♭-, this would assign F, F♯, A♭, B, D as the most probable continuations, the C and A as less probable continuations, and the E♭, G, E, and D♭ as even less probable. One could further simplify this view by remembering the distribution that exists around the mean of 7 to 10 notes that reflects a realistic analysis of the frequency of the lengths of non-duplicative root successions.
A means of creating a sense of focus on a particular note or harmony is inversional symmetry. Take, once again, the F, F♯, A♭, B, and D in relation to C+E♭+A+E♭-G+E+D♭+B♭-. Since the 8-note incipit goes on to include the remaining five pcs of the aggregate, the continuations to D+, B+, A♭+, F+, E♭+, F♯-, and C+ evince something significant. If C is to be established as root of the central harmony, all other chords in this progression should be found to balance around C at the same time they are pressing on toward a seven- to ten-note, well-formed fundamental bass that is devoid of internal repetitions. This can be seen easily enough: the second chord E♭+, at 3 or 15 semitones above C is balanced by the third chord A+, 3 or 15 semitones below C; the fifth chord G+ is balanced by the fourth to last chord F+; the sixth chord E+ is balanced by the fifth to last chord A♭+; the seventh chord D♭+ is balanced by the sixth to last chord B+; and the eighth chord B♭- is balanced by the seventh to last chord D+. In a kinematic diagram, the 2 that is the third term in the prime-form path [0123456789te] would be followed by an arrow that goes to e which is itself followed by an arrow that goes to 8 that is followed by an arrow that goes to 5, spelling out with these tonicized triad roots the components of what is vii07 in the key of C and prosecuting a “heavy” sweep to C+, the axis of symmetry and the central tone of the passage. One may remember from Example 9 that for B+D+F+A+A♭+C+E♭+G-B♭+C-D♭+ there are four pairs of pcs that balance around C in the progression.
The fifth column in the table located in the Appendix is labeled “(INT Cycle/Collectional Superset(s)),” and shows for a given harmonic class the referential set(s) or interval cycle(s) to which the class bears a degree of kinship. For example, for a harmonic class with no apparent relatedness to a diatonic, octatonic, hexatonic, or whole-tone collection, the likeliest generating pc intervals that account for the content of a harmonic class belong to the C1-, and C5-cycles, respectively. The column under the “P(A|B)” heading gives the conditional probability that a harmonic class (expressed as a pc set) will actually become the referential collection(s)/interval cycle(s) of which it is a subset. The last column under the “P(B|A)” heading expresses the conditional probability that a harmonic class (expressed as a pc set) is actually derived from the referential collection(s)/interval cycle(s) of which it is a subset. 1 in the former column would have 0 in the latter, indicating a harmonic class (expressed as a pc set) that is not merely derived from but actually is one of the four large collections that have attracted the most compositional and theoretical attention (i.e., diatonic, octatonic, hexatonic, and whole-tone). The numbers in between flesh out the continuum of the communicating class (to borrow a Markovian term) of referential sets and harmonic classes or, rather, between no bias and complete bias in favor one of the four major collections or one of the six interval cycles and their transpositions. In the case of a harmonic progression belonging to class 7-31, the cardinality is seven, meaning that there are five remaining pcs in the aggregate, but only one of those is needed if 7-31 is to become OCT0,1; therefore, the value is 1 - 1/5 or .8 in favor of a bias toward OCT0,1. This high number represents a strong negative correlation with the probability (.2) that 7-31 will, in fact, become OCT0,1. Because they seem to have their origins in either the C1- or C5-cycle, saturational harmonic progressions are often assigned a value of 1 in the former column (i.e., 100% probability that the set will go on to comprehend the aggregate) and 0 in the latter (i.e., 0% probability that the set is not the result of generating pc intervals 1, 11 and/or 5, 7).
Ex. 13. Biased analysis of Many Many Cadences, measures 1-6, (compare with example 7a).
Example 13 revisits the opening of Many Many Cadences, where the enclosures contain the harmonic class (7-31) to which both tonicized root successions belong, and the value between 0 and 1 in the callouts indicate the collectional bias of this harmonic class. The harmonic progression starts on its “tonic” with negligible bias, then the bias increases with the arrival of D♭, forming with the following B♭ harmonic class 7-31. Consulting the table in the Appendix, harmonic class 7-31’s strong association (.8) with OCT0,1 begs to be extended with an F♯ to harmonic class 8-28, since this is the sound world implied by its linear structural properties. However, the basse fondamentale of tonicized roots descends 9 semitones to D. This demonstrates how an emergentistic model accounts for the earlier observation of the compositional decision at this point in Macklay’s harmonic progression to go to a chord other than F♯+ or F♯- that nonetheless contains the pc F♯ as a chord member.
The probability that 7-31 will become an octatonic scale, amazingly enough, predicts this decision: 7-31, with 1:4 odds against it, only has a .2 probability of becoming a “diminished scale.” After its continuations from D+ to F♯- that begins to invoke OCT2,3, the progression rests on C+, which by no means completes that collection (.8), but comes as close to completing it as the first half of the chord progression came to completing OCT0,1. Example 14 revisits the B section and its recurrent sc(0136) root progression, an important subset of harmonic classes 10-1, 8-18, and 7-31. This four-chord succession stays centered on C because it begins with that pc root and the succession is repeated, untransposed, four times after its first presentation; the bias in favor of OCT2,3 (.5) is almost self-evident, and is promoted by the root of the third chord of each of the two preceding four-chord successions which expands the collection to [9,11,0,2,3,6] with a .67 bias in favor of OCT2,3. The repetitions of the sc(0136) harmonic progression continue until the D♯+ in measure 130, where the probability that the subsequent progression will develop into HEX3,4 begins to become much higher (one possible outcome (1) divided by the only favorable outcome (1) with the continuation to the terminal C+ in measure 136). This provides an element common to the ensuing OCT1,2 subset on C and to HEX3,4, namely, pitch set [0,3,4,7], whose members (as triadically harmonized roots) constitute harmonic class 4-17, but, in this case, a C triad with both major and minor third. Thus, it links the contrasting B section with sections A and A1. The harmonic organization of the transition between B and A1 involves contrasting hexatonic and octatonic collections, with an important interaction and link between the two that happens to be emblematic of the “tonic” of the entire quartet. This change in collectional bias from OCT2,3 to HEX3,4 at the end of B through to OCT1,2 of the first three measures of A1 is analogous to the effect of the minimal Schenkerian Ursatz I-V-I, and so is another place in this piece where the tonal cadential analogy works.
Ex. 14. Biased analysis of Many Many Cadences, measures 108-36.
CONCLUSION
In her program notes from a performance of Many Many Cadences by the Mivos Quartet in a concert of works by Columbia University graduate composers held on Friday, February 27th, 2015 at 8:00 PM, Macklay talks about placing functional harmony within a contemporary context as she describes and defends her return to more traditional idioms. She notes that even in the year 2015 “Western ears are vey sensitive to certain formulaic chord progressions commonly used at the ends of phrases in tonal music (cadences).” It is for this reason that, in speaking for herself, and for many similar composers of the early 21st century, she states her intention to “stretch the listener’s perception of cadences by recontexualizing these predictable chord progressions in very fast cells that are constantly changing key and register.” In her final sentence, Macklay’s tone is that of a composer who has found a new path of development for old material: “These lonely, disjunct ends of phrases eventually congeal and transform into new kinds of phrases and sound objects.”29Macklay (2015).
The “neo” in Macklay’s “neoconservative postmodernism” may therefore signify more than an expression of the Ovidian adage omnia mutantur, nihil interit30Naso (8 AD/1838), book XV, line 106. and recontextualization. It may also signify the discovery of something that, while theoretically identical to pre-modern functional tonal expectations, stems in its balance of chance and determinism from the undivided wholeness of two harmonic characteristics that, prima facie, do not appear to lend themselves to common-practice tonality. Ic1/2 voice-leading parsimony and dual-process, contextual-fluid inversion employ the two most common interval classes in all referential collections, and pc-center motivic projection offers one means, akin to Schoenberg’s conception of the twelve-tone system, to avoid a bias toward a central pitch.31Schoenberg (1948/1984): “The construction of a basic set of twelve tones derives from the intention to postpone the repetition of every tone as long as possible. I have stated in my Harmonielehre that emphasis given to a tone by a premature repetition is capable of heightening it to the rank of tonic. But the regular application of a set of twelve tones emphasizes all the other tones in the same manner, thus depriving one single tone of the privilege of supremacy. It seemed in the first stages immensely important to avoid a similarity with tonality.” (246) As Pieter van den Toorn puts it, “With Schoenberg, connections were pursued primarily from the standpoint of motives..., while, with Schenker, they were pursued from that of harmony and voice leading...,” but Schoenberg and Schenker were both right because “in a larger sense,” motive, harmony, and voice leading make up “an organic whole, of parts reciprocally both defining and being defined by a whole...”32van den Toorn (1996), n. 3, 373, 389. Harmonic progressions of triads may thus be compared to anything that is undergoing transformation if they not only correspond to the tracing of a motivic path but also if the content of each chord can be transposed or inverted into the content of the next, and these mappings can be said to fuse and negate both motivic projection and triadic transformations at the same time. For example, if one keeps in mind the unchanging texture of the superimposition of thirds on the pc-roots of the Macklay kinematic, one will see that the presence of both motivic and transformative processes are without distinction, even though the pc-root content can often be placed in normal form as a segment of a referential collection. Everywhere, the assimilation of both principal means of harmonic successions may be taken for granted. Motivic connections and underlying linear progressions, and the orthodox Schoenberg-versus-Schenker antagonism between the two, may be regarded as a false dichotomy, especially if one is interested in placing one’s confidence in the ability of the Macklay kinematic to reflect the “organic” character of her music. The nondemarcation of these two features can be identified simply as “transformation” and is taken into account without being openly or officially expressed as a column in the Appendix: it is tacitly presupposed in the grouping of the immediately adjacent chords of every appearance of every chord into harmonic classes. The abstract descriptions of non-binary integration of the two principal types of triadic post-tonality involved in Macklay’s recontextualization and van den Toorn’s “organic whole” bear a striking resemblance to each other.
Appendix. The Macklay Set partitioned into harmonic classes.
Notes
1 Macklay (n.d.). Macklay’s website can be accessed here: https://www.skymacklay.com/, while a YouTube video of Many Many Cadences (with score) as performed by the Spektral Quartet (http://spektralquartet.com/) can be accessed here: https://www.youtube.com/watch?v=mrI39Nf7cj4.
2 Tymoczko (2008a), 1–49.
3 Bernard (1995), 284. The validity of this appellation is immediately recognized by skimming through the score of Many Many Cadences which, while incorporating glissandi or, rather, portamenti into most of its melodic motions (29 out of the 39 pages of the score call for these microtonal elements), is saturated with common-practice formulaic chord progressions or the use of triads in other ways.
4 Tymoczko (2008a), 1-49.
5 Murphy (2007), 217, n. 1.
6 Tenney (1977), 36-69, n. 1.
7 Slottow (2009), 25. Ruggles’ application of pitch-class nonrepetition is very similar to its application in Macklay (2014). As in Ruggles’ melodies, one cannot assign a non-duplicative pc-root succession to every chord in a Macklay fundamental bass; the flexibility of the actual length of these successions is measured as the average number of non-duplicating pc-roots that lead up to and include the pc. Although this is a sound method for computing a general figure for the number of intervening notes one might expect to find in a composer’s motivic pathways, it slightly undervalues those instances in which that number fluctuates wildly from the norm to a greater or lesser extent, which is more in accordance with the present interest (which was often Ruggles’ own) in persistent motivic repetition.
8 Cowell (1974): “Ives’s melodies often change key implication very rapidly so that in spots they may suggest atonality. Usually, however, they are plainly major, minor or chromatic; rarely are they modal or genuinely atonal.” (164) Likewise, Macklay’s highly accelerated harmonic rhythm in Many Many Cadences may be teased from the application of the Ivesian principle because it underlies Macklay’s harmonic practice, involving as it does a wide variety of pc-roots as simultaneously avowing and disavowing tonal expectations.
9 Searby (2001), n. 216: “... Ligeti completed his Horn Trio - which uses traditional ternary form, a passacaglia (although a disguised one), a strong melodic focus, and a harmonic language which contains clear triads and dominant sevenths in abundance. In spite of his assertions above, it does seem as if Ligeti, in addition to rejecting the Avant-garde, is looking to the past for major elements of his musical language. However, in so doing he avoids the imitation of stylistic features of past music, so prevalent in neo-Romantics such as David Del Tredici and George Rochberg. Ligeti clearly detests such an approach.” (17)
10 Rameau (1722/1971): “The essence of composition, for harmony as well as melody, lies principally, especially at present, in that bass we call fundamental.” (206)
11 Pitch class A is included in some vertical sonorities, but not in the root progression itself.
12 Tymoczko (2008a), 49.
13 Lewin (2002), n. 2, 196-230.
14 Hook (2007), 15.
15 Roeder and Cook (2006), 46, 55, 66.
16 Tymoczko (2008a), 10.
17 Cohn (1998), n. 2, 170.
18 Gollin (2011), 388. It is interesting to note that, in a discussion of the possibility of a dual-process, contextual-fluid, inversional triadic transformation, sc(02469) is found in a taxonomic list of Riemann’s doppelklänge (double sounds) as a pentachordal set that has been generated by the triadic combination of a major chord and its minor dominant (e.g., D+ and A-).
19 Ibid., 388. Again, it seems quite a coincidence, especially in the present twofold operational context, to come across another binary combination of triads which together generate a pentachordal set (in this case, sc(01348)) that, like sc(02469), is equivalent to one of Riemann’s doppelklänge (double sounds; e.g., A♭+ and D♭-).
20 Mellers, (1963 - 1964), 1. For example, in music that has this post-1945 tendency to include a type of experimentalism (still alive today) that is characterized by the rejection of tonality, it generally falls into circumscribed areas of Eurocentric, chauvinistic, and genre-specific analysis, in spite of the growing “rearguard” return to tonality mentioned earlier as a mark of neoconservative postmodernism. Many Many Cadences is undoubtedly both a consequence of, and a paradoxical hybridization of viewpoints, a consequence of both 500 years of the Cartesian dualism that distinguishes between mind and body (or between mind and world), and a nondualistic dissolution of the Kantian categorical distinction between, for instance, “me” and “not-me.” The Renaissance, as a period of cultural advancement in contrast to the Middle Ages, has been called into question. The 14th–17th centuries, seen by some as a period of pessimism and nostalgia for classical antiquity, may be compared to the peculiarly 21st-century American phenomenon marked by a “nostalgia” for the triadic harmonic language of roughly the time from 1600 to 1900. Nondualistically considered, contemporary American culture still has ambitions of advancement while at the same time looking to the past for some overlooked or forgotten means of satisfying that ambition.
21 Thus, the kinematic diagrams of this paper concern themselves purely with motion and not with what causes that motion. This is basic to the very definition of kinematics: the study of motion without regard to its cause. Therefore, one must be careful not to confuse kinematics with kinetics: the study of motion as caused by forces and moments.
22 Mellers, (1963 - 1964), 2.
23 Ligeti (1965), 5-19. In this essay, Ligeti introduced the concept of musical “permeability” according to which a musical structure is “permeable” if it allows a free choice of intervals. The word is used here in a similar fashion to refer to a musical state which allows for free choice of successive triads. Thus, in the same way that Ligeti saw permeability in serial music as a substitute for the form-shaping function of melodic lines, motifs, and harmonies in older styles, the present author sees permeability in Macklay’s triadic post-tonality as equivalent to the form-shaping function of serialism.
24 Tymoczko (2008), 1–49.
25 Ibid.
26 Tymoczko (2010), 42.
27 Morris (1983/1984), 187-217.
28 Morris (1987), 107.
29 Macklay (2015).
30 Naso (8 AD/1838), book XV, line 106.
31 Schoenberg (1948/1984): “The construction of a basic set of twelve tones derives from the intention to postpone the repetition of every tone as long as possible. I have stated in my Harmonielehre that emphasis given to a tone by a premature repetition is capable of heightening it to the rank of tonic. But the regular application of a set of twelve tones emphasizes all the other tones in the same manner, thus depriving one single tone of the privilege of supremacy. It seemed in the first stages immensely important to avoid a similarity with tonality.” (246)
32 van den Toorn (1996), n. 3, 373, 389. Harmonic progressions of triads may thus be compared to anything that is undergoing transformation if they not only correspond to the tracing of a motivic path but also if the content of each chord can be transposed or inverted into the content of the next, and these mappings can be said to fuse and negate both motivic projection and triadic transformations at the same time. For example, if one keeps in mind the unchanging texture of the superimposition of thirds on the pc-roots of the Macklay kinematic, one will see that the presence of both motivic and transformative processes are without distinction, even though the pc-root content can often be placed in normal form as a segment of a referential collection. Everywhere, the assimilation of both principal means of harmonic successions may be taken for granted. Motivic connections and underlying linear progressions, and the orthodox Schoenberg-versus-Schenker antagonism between the two, may be regarded as a false dichotomy, especially if one is interested in placing one’s confidence in the ability of the Macklay kinematic to reflect the “organic” character of her music. The nondemarcation of these two features can be identified simply as “transformation” and is taken into account without being openly or officially expressed as a column in the Appendix: it is tacitly presupposed in the grouping of the immediately adjacent chords of every appearance of every chord into harmonic classes.
References
Bernard, Jonathan W. 1995. “Theory, Analysis, and the “Problem” of Minimal Music.” In Concert Music, Rock, and Jazz since 1945: Essays and Analytical Studies, 259-84. Edited by Elisabeth West Marvin and Richard Hermann. Rochester, NY: University of Rochester Press.
Cohn, Richard. 1998. “Introduction to Neo-Riemannian Theory: A Survey and a Historical Perspective,” Journal of Music Theory 42, no. 2 (Autumn): 167-80.
Cowell, Henry and Sidney Cowell. 1955. Charles Ives and His Music. Reprint, New York: Oxford University Press, 1974.
Darcy, Warren. 1997. “Bruckner’s Sonata Deformations.” In Bruckner Studies, 256–77. Edited by Timothy L. Jackson and Paul Hawkshaw. Cambridge: Cambridge University Press.
Gauldin, Robert. 2004. “The Theory and Practice of Chromatic Wedge Progressions in Romantic Music,” Music Theory Spectrum 26, no. 1: 1-22.
Gollin, Edward. 2011. “On a Transformational Curiosity in Riemann’s Schematisirung Der Dissonanzen.” In The Oxford Handbook of Neo-Riemannian Music Theories, 382 – 99. Edited by Edward Gollin and Alexander Rehding. New York: Oxford University Press.
Harrison, Daniel. 1994. Harmonic Function in Chromatic Music. Chicago: University of Chicago Press.
Hinton, C.H. 1884. “What is the Fourth Dimension?” In Vol. 1 of Scientific Romances, 1-22. London: W. Swan Sonnenschein & Co.
Hook, Julian. 2007. “Cross-Type Transformations and the Path Consistency Condition.” Music Theory Spectrum 29: 15.
Kostka, Stefan and Dorothy Payne. 2004. Tonal Harmony, With an Introduction to Twentieth-Century Music. Boston: McGraw-Hill.
Ligeti, György. 1965. “Metamorphoses of Musical Form” [“Wandlungen der musikalischen Form”]. Translated by Cornelius Cardew. English edition, Die Reihe: Form-Space, 7: 5-19.
Lewin, David. 2002. “Thoughts on Klumpenhouwer Networks and Perle-Lansky Cycles,” Music Theory Spectrum 24, no. 2 (Fall): 196-230.
Macklay, Sky. n.d. “about.” http://www.skymacklay.com/. Accessed August 12, 2015.
---. 2014. Many Many Cadences: A String Quartet. New York: Sky Macklay.
---. 2015. “About Many Many Cadences.” In Program Notes from JACK Quartet and Mivos Quartet Performing New Works by Columbia University Graduate Composers. New York.
---, composer. 2016. Many Many Cadences. On Serious Business. Spektral Quartet. Sono Luminus, CD.
Mellers, Wilfred. 1963 – 1964. “The Avant-Garde in America,” Proceedings of the Royal Musical Association 90th Session. Taylor & Francis, Ltd. on behalf of the Royal Musical Association: 1-13.
Moreno, Rodolfo. 2017. “Harmonic Syntax and Vocabulary in Tonal Music.” Abstract from Le IXe Congrès européen d’Analyse musicale.
Morris, Robert. 1983/1984. “Set-Type Saturation Among Twelve-Tone Rows,” Perspectives of New Music 22 (Fall-Winter 1983/SpringSummer 1984): 187-217.
---. 1987. Composition with Pitch Classes. New Haven: Yale University Press.
Murphy, Scott. 2007. “A Model of Melodic Expectation for Some Neo-Romantic Music of Penderecki.” Perspectives of New Music 45, no. 1 (Winter): 184-222.
Naso, Publius Ovidius. 8 A.D. Book XV. In Metamorphoseon, 154-67. Edited by George Ferguson (LL.D.). Edinburgh: Oliver & Boyd, 1838.
Piston, Walter. 1941. “Tonality and Modality.” In Harmony, 47-65. 4th ed. Revised and Expanded by Mark DeVoto. New York: Norton, 1978.
Rameau, Jean-Philippe. 1722. Traité de l’harmonie réduites à ses principes naturels. Translated by Philip Gossett. Reprint, Mineola, NY: Dover Publications, Inc., 1971.
Riemann, Hugo [Hugibert Ries, pseud.]. 2000 [1872]. “Musical Logic: A Contribution to the Theory of Music,” translated by Kevin Mooney. Journal of Music Theory 44/1: 100–26.
Roeder, John and Scott Alexander Cook. 2006. “Triadic Transformation and Parsimonious Voice Leading in Some Interesting Passages by Gavin Bryars,” Intégral 20: 43-67.
Schoenberg, Arnold. 1975. “Composition with Twelve Tones (2) c. 1948.” In Style and Idea: Selected Writings of Arnold Schoenberg, 245-9. Edited by Leonard Stein. Translated by Leo Black. Reprint, Berkeley: University of California Press, 1984.
Searby, Mike. 2001. “Ligeti’s ‘Third Way’: ‘Non-Atonal’ Elements in the Horn Trio,” Tempo (New Series), no. 216 (April): 17-22.
Slottow, Stephen P. 2009. A Vast Simplicity: The Music of Carl Ruggles. Vol. 8 of Dimension & Diversity: Studies in 20th Century Music. Hillsdale, NY: Pendragon Press.
Straus, Joseph Nathan. 2005. “Centricity, Referential Collections, and Triadic Post-Tonality.” In Introduction to Post-Tonal Theory, 158-66. Upper Saddle River, N.J.: Prentice Hall.
Tenney, James. 1977. “The Chronological Development of Carl Ruggles’ Melodic Style.” Perspectives of New Music 16, no. 1 (Fall-Winter): 36-69.
Tymoczko, Dmitri. 2008a. “Scale Theory, Serial Theory, and Voice Leading.” Music Analysis 27/1: 1–49.
---. 2008b. “Set-Class Similarity, Voice Leading, and the Fourier Transform.” Journal of Music Theory 52/2: 251–272.
---. 2010. A Geometry of Music: Harmony and Counterpoint in the Extended Common Practice. New York: Oxford University Press.
van den Toorn, Pieter C. 1996. “What’s in a Motive? Schoenberg and Schenker Reconsidered,” The Journal of Musicology 14, no. 3 (Summer): 370-99.
White, Christopher Wm. 2013. “Some Statistical Properties of Tonality, 1650–1900.” PhD diss., Yale University.
Xenakis, Iannis. 1992. “Markovian Stochastic Music-Theory.” In Formalized Music: Thought and Mathematics in Composition, 43-79. Harmonologia Series 6. Hillsdale, NY: Pendragon Press.


