Abstract
The literature of the early part of the twentieth-century poses a unique set of pedagogical challenges when introducing it to the undergraduate population. On the one hand, there are elements that continue in the common-practice tradition, such as phrase structure; on the other hand, there are elements that foreshadow the new, post-tonal vocabulary, such as the whole-tone collection. The trick is to devise exercises and activities that will evince both features. To that end, the present paper offers some suggestions to achieve just that by presenting a detailed analysis of Scriabin’s Prelude, Op. 31, No. 4 (1903). The first part of the paper provides a harmonic analysis that demonstrates the tonal features of the prelude. Next, the phrase structure is examined, specifically the sentence, by comparing it with other pieces in the literature that use a similar convention. Continuing on, whole-tone elements used by the composer are revealed with the use of pc-set analysis. Lastly, the formal design is discussed in the historical context in which the prelude was written. It is hoped that the ideas and activities presented in each section of the paper will create a more nuanced and meaningful discussion in the classroom.
One of the challenges of teaching an undergraduate, introductory class in post-tonal theory is how best to address literature that has both traditional and non-traditional elements.1 Many students have been led to believe that with the advent of the twentieth century a rupture in compositional practice occurred that irrevocably separated the new from what came before.2 While the distinct harmonic palette present in the atonal music of the Second Viennese School, for instance, does mark a departure from common-practice tonality, it is not accurate to understand such compositions as completely divorced from other common-practice conventions such as phrase structure and formal design. Moreover, when one considers Schoenberg’s preferred term “pan-tonality” – that this music is not devoid of a prevailing tonality but is infused with competing tonalities – it is important to consider any tonal glimmerings that may be present.
To that end, the present discussion offers an intensive analysis of Scriabin’s Prelude, Op. 31, No. 4 (1903) that will provide some suggestions for in-class discussion. The objective of this paper is to generate some useful ideas on the presentation of this repertoire for the novice and intermediate student. Furthermore, this analysis will address tonal elements, post-tonal elements, phrase structure, and issues of formal design. Regarding the post-tonal elements, the composer makes use of the whole-tone collection and suggestions will be offered regarding the use of pitch-class set analysis for beginning students. Additionally, other examples from the literature will be included in the preliminary sections, while the final section will focus on the prelude exclusively. The following discussion, therefore, is intended to provide pedagogical strategies that will allow the instructor to encourage a more meaningful and comprehensive classroom discussion.
The set of four preludes in Op. 31 were written in a very productive year for Scriabin. Indeed, his compositional output in 1903 includes the Third Symphony – the Divine Poem – and the Fourth Piano Sonata.3 This prolific output also comes at a time when Scriabin’s compositional strategies were changing. Some scholars have delimited the composer’s oeuvre into three periods, and the compositions from 1903 onwards mark the beginning of the middle, or “transitional” period.4 The Prelude, Op. 31, No. 4 falls at the beginning of this period and provides an ideal opportunity in which to study a work that is still tonal but is simultaneously infused with non-traditional elements, specifically the whole-tone collection. As a result, there are harmonies present that cannot be understood satisfactorily in a tonal context, and the use of pitch-class set theory will help evince the embedded whole-tone collection. Perhaps most importantly, the homophonic and homorhythmic texture of this work creates a transparent setting for the harmonic and melodic content; to be sure, it might be better thought of as an etude given its didactic nature.
When introducing this Prelude to the students, a volunteer is asked to play through it; then, the class is divided in half and, using the solfeggio syllables, one half of the class sings the melody while the other half sings the bass line.5 The two groups switch parts for the second sing through, after which students are broken up into small groups to encourage student-to-student interaction. Specifically, they are asked to share their immediate impressions of the music – to engage in a pre-analysis discussion. It is helpful to provide some general questions to get the ball rolling: Does the music sound tonal or atonal?6 If tonal, what is the tonal center of the piece? Which descriptive terms would you use to describe the melodic contour? Do you hear any repeating patterns in the music?7
After the pre-analysis discussion, students are asked to complete a roman-numeral/figured bass analysis of the first eight measures of the prelude (in the measures where there is a dotted-half note in the melody, the students are only asked to identify the harmony on the downbeat – a promissory note is given indicating that the chromatic notes will be addressed later on). Before starting, the students are asked to review their discussion about whether they heard a prevailing tonality, and, if so, what it was; those groups that had a consensus of students say ‘yes’, will most often correctly identify the key of C major (the perfect authentic cadence at the end is a giveaway)8; those groups that had a consensus of students say ‘no’, will require some extra attention from the instructor to determine which features of the music are leading them to that conclusion.
Scriabin, Prelude, Op. 31, No. 4: Helping Students Contextualize the Tonal Elements
Example 1 shows a roman-numeral/figured-bass analysis of the first eight measures. The students should have identified primarily diatonic harmonies in the first four measures: a first-inversion tonic chord at the anacrusis, moving to a dominant chord on the downbeat of m. 1, to an applied chord on the downbeat of m.2, to a subdominant chord on the downbeat of m. 3, to a root-position tonic chord on the downbeat of m.4.9 When these chords are played in succession, without the intervening chromatic diminutions, the students will more readily perceive the diatonic chord progression. The next four measures provide an ideal opportunity to review the Neapolitan chord and two mode-mixture chords, namely ♭VI & ♭III.10 Lastly, the passage concludes with a half cadence.

I now return to the pre-analysis question posed to the students about hearing repeating patterns in the music. Typically, many of them hear the sequential pattern in the bass voice (down a fourth/up a third).11 To reinforce this pattern for the benefit of the students who do not perceive it, students are asked to sing the bass line on the downbeats only. At this point, the students are aware of the harmonies used in the opening eight measures and of a sequential pattern, specifically a descending pattern used in the first four measures. Indeed, the use of the descending sequential pattern is important because it informs the roman-numeral/figured-bass analysis in the opening passage.
The analysis in Example 1 is analyzed in C major; however, mm. 2–4 are also analyzed in B♭ major to reflect that the second leg of the sequence begins a whole step below the first leg – a repetition of the basic idea. By doing so, students will be able both to hear and to see that Scriabin has utilized the same harmonic progression and thereby tonicizes this key.12 Furthermore, it is important to show the analysis in both keys because, while the first four measures can be understood in the home key of C major – moving from a first-inversion tonic to a root-position tonic – the analysis of the second two-measure unit in B♭ major demonstrates that the descending sequence is both melodic and harmonic.
Example 2a shows the opening two measures of Chopin’s well-known Prelude in c minor, Op. 28, No. 20 (1838/39). A strong correlation between the two preludes is apparent because Chopin, too, uses a descending sequential pattern – both melodic and harmonic – that briefly tonicizes another key area.13 The roman-numeral/figured-bass analysis in c minor is incomplete as it stands because, although it literally identifies the spelling of the chords of m. 2 in the context of the home key, it does not evince the sequential pattern utilized by Chopin.14 Indeed, the embedded phrase model he builds into the sequential pattern can only be demonstrated by completing an analysis in A♭ major; in so doing, it is clear that the pattern is replicated down a major third, and the harmonic progression of i to iv to V to i (with the underling syntax of T – PD – D – T) is repeated in this new, temporary environment.
Next, Example 2b shows the opening five measures of Mozart’s Fantasy No. 4 in c minor (1785). Again, the listener is confronted with a two-measure basic idea that is both repeated and transposed; indeed, it is restated down a whole step in b♭ minor. What is more, the underlying syntax of tonic to dominant provides another similarity with the Scriabin passage. In addition, the localized tonic areas exploited in the opening of the Fantasy follow the same trajectory as Scriabin’s prelude: c – b♭ – A♭. Consequently, it is important to acknowledge that there are two examples in the tonal repertoire – Chopin & Mozart – from which Scriabin might have drawn inspiration and that underscore a connection with the past.

Returning to Example 1, the analyses in two keys also show that the harmonic progression used by Scriabin in the first four measures employs back-relating dominants.15 Conceptually, a back-relating dominant is understood as prolonging a harmony that precedes it rather than providing impetus to a harmony that follows it. In the analysis, a bi-directional arrow is used to highlight this unique relationship (although the back-relating dominant is understood as prolonging what comes before – a distinction drawn after the fact that is depicted by reading the arrow from right to left – aurally, the ear hears the dominant as following the chord it prolongs that is depicted by reading the arrow from left to right). In addition, these back-relating dominants punctuate the end of each two-measure unit, which will be addressed more completely when the phrase structure of the prelude is discussed.
Lastly, the ear hears what may be the beginning of a third leg of the sequence at the end of m.4; the sequential pattern used by Scriabin yields another first-inversion triad down a whole step (see the analysis in A♭ major). Notwithstanding, it is not a complete leg because the sequential pattern is abandoned in favour of a prolongation of the Neapolitan chord (see mm. 5–6) in its traditional role as a pre-dominant harmony (the ♭III harmony in m. 6 is a voice-leading chord that facilitates a voice exchange, which is why the roman numeral is parenthesized in the analysis). Similarly, the dotted-rhythm is used one final time before being abandoned in favour of a series of sustained notes; indeed, both the harmonic rhythm and the surface-level rhythm are drawn out to prepare the ear for the arrival of the half cadence.
Indeed, if one studies the voice leading that Scriabin uses in this opening passage, a cohesive and traditional design is made plain. Example 3 shows a voice-leading schema of the first eight measures. It is comprised mainly of first-species counterpoint with imperfect consonances. Additionally, there are two instances of second-species counterpoint, specifically the 5-6 technique. The notes in the second half of these two measures are derived via the use of mode mixture, and they create neighbours – complete in the first instance and incomplete in the second instance – to the notes of the main melody. Lastly, there is an accented dissonance that is construed as an instance of fourth-species counterpoint.16 The conventional design present in the schema is remarkable given that Scriabin has also infused the musical fabric with post-tonal elements. Example 3 provides compelling evidence that Scriabin’s compositional practice demonstrates a clear connection with voice-leading practices of the past.

There is one vertical sonority that has yet to be identified, which occurs on the sixteenth note in the anacrusis and has been simply labelled as (![]() ) to reflect the augmented sixth above the bass. This sonority sounds similar to a familiar harmony identified in Example 4a, which shows a German augmented-sixth chord in the key of G major.17 What is unique about this chord is an alternate spelling; specifically,♭
) to reflect the augmented sixth above the bass. This sonority sounds similar to a familiar harmony identified in Example 4a, which shows a German augmented-sixth chord in the key of G major.17 What is unique about this chord is an alternate spelling; specifically,♭![]() , me, or B♭, has been respelled as ♯
, me, or B♭, has been respelled as ♯![]() , ri, or A♯, which is more intuitive given that the raised scale degree resolves upwards to mi in the cadential six-four that follows. This revised spelling is often referred to as a doubly-augmented-fourth chord because the quality of the fourth above the bass is doubly augmented (in this instance, E♭ to A♯). Moreover, this augmented-sixth chord is used in the traditional syntactical role of a pre-dominant. It is interesting to note that, with the exception of the A♯, this chord is identical to the chord in the anacrusis of the Prelude (shown in letter d by the solid noteheads).
, ri, or A♯, which is more intuitive given that the raised scale degree resolves upwards to mi in the cadential six-four that follows. This revised spelling is often referred to as a doubly-augmented-fourth chord because the quality of the fourth above the bass is doubly augmented (in this instance, E♭ to A♯). Moreover, this augmented-sixth chord is used in the traditional syntactical role of a pre-dominant. It is interesting to note that, with the exception of the A♯, this chord is identical to the chord in the anacrusis of the Prelude (shown in letter d by the solid noteheads).

Example 4b shows a passage from Scriabin’s Prelude, Op. 13, No. 3, mm. 16–18 (1895). The prelude, in G major, includes an extended tonicization of B♭ major and A♭ major. The excerpt in 4b shows the end of the extended tonicization of the key of the Neapolitan that simultaneously becomes the beginning of the final progression in the home key of G major. Thus, I in A♭ major can be construed as a pivot that is also understood simultaneously as ♭II in G major, which fills the syntactical role of a pre-dominant in the final progression. Immediately after the Neapolitan chord, the vertical sonority discussed in Example 4a materializes (it is identified with an arrow); however, whereas it is spelled identically, its configuration has been altered.18 Note that ♯![]() , ri, or A♯, has now been placed in the bass voice and ♭
, ri, or A♯, has now been placed in the bass voice and ♭![]() , le, or E♭, has been placed above the bass in an inner voice.19
, le, or E♭, has been placed above the bass in an inner voice.19
More importantly, this harmony does not move to the dominant; instead, it moves directly to the tonic. Thus, the augmented sixth between E♭ and C♯, resolves not to the root of a dominant but to the fifth of a tonic. 20 What is the implication of this voice-leading technique? In short, the syntactical role of this sonority has changed so that it now assumes a dominant character rather than a pre-dominant character. Specifically, Scriabin exploits a parallel tenth motion between the outer voices that creates two leading tones directed to the third and fifth of the I6 harmony, which is a particularly effective device to affirm the tonic (the root has already been introduced via common tone). Given the stepwise motion to the first-inversion tonic, the final progression may be identified as a contrapuntal cadence.21
Example 4c again shows the same vertical sonority but this time the German augmented- sixth is spelled conventionally with me (see the solid noteheads).22 Here, the augmented-sixth sonority is a voice-leading chord that prolongs a G major harmony; the G4 is held as a common tone while two of the other voices move by semitone and the bass voice moves by third.23 Unlike its incarnation in the first two examples, the vertical sonority here does not advance the underlying harmonic syntax because it is used exclusively as an agent of prolongation. To sum up, the three examples of the German augmented-sixth chord reviewed thus far have demonstrated that its syntactical role is context specific.24
The final example, letter d, presents the anacrusis of the Prelude, Op. 31, No. 4 (the note values have been augmented for clarity). As stated previously, the vertical sonority that appears in the solid noteheads is almost identical to the German augmented-sixth chord; the sole exception is that the sonority includes ![]() , or B♮, rather than ♭
, or B♮, rather than ♭![]() , or B♭.25 One possible interpretation is an Italian augmented-sixth and the idiosyncratic B4 is an anticipation. While that label is somewhat satisfactory, it does not address the amorphous attributes of this vertical sonority. First, like the common-tone augmented-sixth chord shown in letter c, G4 is maintained as a chord tone throughout and the bass voice moves by third to the final chord rather than by semitone (contrast with letters a & b). Next, as this sonority acts as a conduit between a tonic harmony and a dominant harmony, one might be inclined to interpret it in the syntactical role of a pre-dominant like letter a; however, in the key of C major, an Italian augmented-sixth chord would be spelled as C, A♭, & F♯, and a German augmented-sixth chord would also include E♭. Hence, the interval of an augmented sixth occurs not between ♭
, or B♭.25 One possible interpretation is an Italian augmented-sixth and the idiosyncratic B4 is an anticipation. While that label is somewhat satisfactory, it does not address the amorphous attributes of this vertical sonority. First, like the common-tone augmented-sixth chord shown in letter c, G4 is maintained as a chord tone throughout and the bass voice moves by third to the final chord rather than by semitone (contrast with letters a & b). Next, as this sonority acts as a conduit between a tonic harmony and a dominant harmony, one might be inclined to interpret it in the syntactical role of a pre-dominant like letter a; however, in the key of C major, an Italian augmented-sixth chord would be spelled as C, A♭, & F♯, and a German augmented-sixth chord would also include E♭. Hence, the interval of an augmented sixth occurs not between ♭![]() and ♯
and ♯![]() but between ♭
but between ♭![]() and ♯
and ♯![]() 26 Alternatively, this vertical sonority can readily be understood in reference to G major; in this reading, it can be contextualized to include ♭
26 Alternatively, this vertical sonority can readily be understood in reference to G major; in this reading, it can be contextualized to include ♭![]() and ♯
and ♯![]() .27 Thus, a case may be made to label this sonority as (
.27 Thus, a case may be made to label this sonority as (![]() )/V if one is to posit these scale-degree inflections, ficta if you will, as normative in augmented-sixth-chord construction (see the harmonic analysis of letter d in reference to the key of the dominant).
)/V if one is to posit these scale-degree inflections, ficta if you will, as normative in augmented-sixth-chord construction (see the harmonic analysis of letter d in reference to the key of the dominant).
Moreover, just as with the augmented-sixth chord in letter b, the vertical sonority in letter d leads not to the dominant of G, or a D major harmony, but directly to G major itself, which instead suggests a syntactical interpretation of this sonority as a dominant. As a result, the amorphous attributes of this vertical sonority – it has been shown to share commonalities with the other three examples – make it difficult to determine a precise syntactical label. Indeed, regarding the various types of augmented-sixth chords, Daniel Harrison concedes that “the intervallic constitution of augmented-sixth chords need not be specified or prescribed since it is the augmented-sixth interval that gives the chord its powers; the remaining notes that accompany the generating interval provide it with different sonorous shadings.”28 Accordingly, a precise syntactical label for this sonority is not the point; how Scriabin uses it to stitch together the tonic and the dominant is, which marks a departure from common-practice conventions.29
Our conversation has become quite nuanced, and it is left to the instructor to determine how much of this information is appropriate for the skill-level of the students; to be sure, one of the challenges of navigating classroom dynamics is to gauge when, and to what degree, it is appropriate to problematize the class material. Thus, for some it may be sufficient for the students simply to recognize the augmented-sixth chords present in the anacrusis and in the pick-up to m. 3. For others, a rigorous discussion of the various incarnations of the augmented-sixth chord may be in order. Either approach is valid because this discussion is meant to supplement a lesson plan and not to commandeer it.
Scriabin, Prelude, Op. 31, No. 4: Making the Case for a Conventional Phrase Structure
I turn now to the phrase structure of the prelude. As mentioned earlier, Scriabin uses a conventional four-measure phrase that is often broken down into two-measure units. Specifically, he uses a formal design in his prelude that is referred to as a sentence, and William Caplin’s ideas about this organizational paradigm will be referenced in this discussion. In addition, three additional examples – two from the Romantic period and one from Scriabin’s oeuvre – are analyzed in order both to review the sentential paradigm for the benefit of the students and to establish that Scriabin’s formal organization is unequivocally in line with the practices of his predecessors. By providing multiple examples, it is hoped that one will be found suitable for the instructor’s lesson plan, and the others may be included in a list of recommended examples for the advantage of the students.30
Turning now to phrase structure, Example 5 shows the second theme from the first movement of Tchaikovsky’s Symphony No. 6 (1893), which, just like the Scriabin excerpt in Example 1, has two four-measure phrases. At this point, it is beneficial to review the salient features of the sentence for the students31. The first phrase of the sentence is referred to as the “presentation,” and it is different from the antecedent phrase of the period because a single harmony is prolonged throughout. Additionally, the end of the phrase is not punctuated by a cadence. Indeed, observe that, in the Tchaikovsky example, the tonic of D major is prolonged throughout the initial phrase via a D pedal, and there is no cadence. In terms of the harmonic progression, there are two dominant, voice-leading chords that prolong the tonic, which have been parenthesized in the analysis.
1I have chosen not to show the actual measure numbers so that the eight-measure sentence, which has become the standard in this discussion, might more easily be observed.
Additionally, the initial phrase may be divided into two-measure units, the first of which has been identified in the analysis as the basic idea. Again, a distinction between the sentence and the period must be drawn: in a presentation phrase, the basic idea is restated, whereas in an antecedent phrase a contrasting idea is declaimed in the second, two-measure unit.32 The simile mark above the second two-measure unit in Example 5 is used to indicate the repetition of the basic idea. Thus, the presentation phrase can be likened to a couplet in poetry, namely, the basic idea and its repetition.
The second phrase of the sentence is referred to as the continuation phrase. Caplin suggests that four phenomena are often found in this phrase: fragmentation of the phrase structure, increase in the harmonic rhythm, increase in the surface-level rhythm, and sequential patterns.33 Regarding fragmentation of phrase structure, the two-measure unit that made up the basic idea is broken down and smaller units are observed; in the case of the Tchaikovsky example, a descending melodic fragment is heard outlining a fourth beginning at the pick-up to m. 5. In fact, it sounds incomplete when heard in isolation. The first phenomenon is identified in the analysis with the abbreviation “frag.”
Next, I will address the fourth phenomenon, sequential patterns, because it is germane to the melodic fragment just discussed. The first fragment, A5 to E5, is immediately followed by another fragment articulated down a step, G5 to D5. Moreover, there is also a harmonic component to this sequence as vii°7/ii to ii is followed by vii°7 to I (the root motion is D♯– E to C♯ – D, which translates to a dominant-tonic progression in each leg, while the second leg has been transposed down a whole step).34 The second phenomenon, an increase in the harmonic rhythm can be heard as the underlying harmonies change every half measure beginning at the pick-up to m.5. Lastly, there is no discernible change in the surface-level rhythm as Tchaikovsky employs the increased harmonic rhythm and the sequential pattern to create the impetus to the cadence in m. 8.
This last point segues to the final component of the continuation phrase, the cadential progression. The melody from the repetition of the basic idea in the presentation phrase is restated over the final harmonic progression that leads to an imperfect authentic cadence (which is shown in the analysis – significantly, m. 7 is the first time a root-position dominant is heard in the theme). However, in the presentation phrase, F♯5 is heard as a consonance against the bass, while in m. 6 this note is now heard as a dissonance against the bass. The voice leading here requires the dissonance to resolve downwards; furthermore, the G♯3 in the bass is itself a tendency tone because it is both the root of the half-diminished seventh harmony and the leading tone to the dominant. Accordingly, Tchaikovsky creates a compelling melodic and harmonic drive to the cadence. This 1 + 1 + 2 design (frag. + frag. + cadence) of the continuation phrase is considered common by Caplin.
Lastly, when considering the entirety of the sentence, there is another important distinction to be drawn with the period. Turning to the vocabulary of poetry once again, the concept of enjambment is invoked.35 This concept describes a line of poetry that prompts the reader to the next line in order to grasp the meaning of the poet; there is no rhetorical break or arrestment of the syntax. Here is an example from Endymion by John Keats:
Nor do we merely feel these essences
For one short hour; no, even as the trees
That whisper round a temple become soon
Dear as the temple’s self, so does the moon,36
Notice, for instance, how the whispering trees “become soon Dear as the temple’s self…” as the reader is prompted to the next line.37 Similarly, in a sentence, there is no rhetorical break between phrases as there is in a period – consider the cadence that occurs at the end of the antecedent phrase – rather, the ear is guided immediately from the presentation phrase to the continuation phrase to comprehend the syntactical meaning of the composer. In the case of the second theme from the Tchaikovsky example, the prolongation of the tonic throughout the presentation phrase to the first half of the continuation phrase guides the listener’s ear to the cadential progression at the end of the latter.38
Next, Example 6 shows the first eight measures of Scriabin’s 13th prelude, in G♭ major from the collection in Op. 11 (1888/96). Here, a similar sentential design may be observed. First there is a four-measure presentation phrase comprised of two-measure units – a basic idea that is repeated (there is both a retardation and a suspension in m. 2 that resolves over a moving bass; the numbers in parentheses show the conventional resolution of each). However, rather than an exact repetition, there is a statement-response relationship. Caplin asserts that this relationship is typified by a restatement of the opening idea over the dominant – a dominant version.39 It is illustrative to have students compare mm. 3–4 of Example 5 with mm. 3–4 of the Example 6 so that the distinction between an exact repetition and a statement/response may be clearly drawn.

What is most unique about the presentation phrase, in comparison to the previous example, is the presence of tonal ambiguity in m. 4. On the one hand, in the harmonic dimension, the dominant is placed in an inversion in m.3 that appears to move to a first-inversion tonic, which is a conventional technique employed to evade a cadence. Additionally, the melody in m. 3 articulates the beginning of an ascending line that hints at ![]() as the goal, but instead
as the goal, but instead ![]() is played (in the reprise of the A material at the end of the prelude,
is played (in the reprise of the A material at the end of the prelude, ![]() is articulated at the final cadence, as shown in Example 7, in order to fulfill the expectations of the listener). On the other hand, a functional progression in the key of the submediant, e♭ minor, commences while, in the melodic dimension, Scriabin begins a descending, harmonic minor scale. Thus, there are two possible resolutions of the dominant indicated in the analysis, both of which evade a cadence: motion to I6 or a deceptive resolution to the submediant.
is articulated at the final cadence, as shown in Example 7, in order to fulfill the expectations of the listener). On the other hand, a functional progression in the key of the submediant, e♭ minor, commences while, in the melodic dimension, Scriabin begins a descending, harmonic minor scale. Thus, there are two possible resolutions of the dominant indicated in the analysis, both of which evade a cadence: motion to I6 or a deceptive resolution to the submediant.
This last point acts as a springboard to a consideration of the continuation phrase. In the Tchaikovsky example, an unequivocal prolongation of the tonic, D major, was achieved primarily via a tonic pedal. Here, in the Scriabin prelude, the key of the submediant is acting as a surrogate for the home key, and the tonic is prolonged, if done so surreptitiously. At the end of the fragmentation in the continuation phrase, m. 6, another instance of tonal ambiguity is encountered: the linear, descending bass line culminates on E♭3 (by playing the left hand in isolation at mm. 5–6, the key of the submediant is apparent); conversely, the second melodic fragment outlines the G♭ major triad (similarly, by playing the right hand in isolation at m. 6, the key of the tonic is apparent).40 The passage then concludes with a half cadence, and the sol to re gesture is repeated. In conclusion, both examples of a sentence demonstrate prolongation of the tonic throughout the presentation phrase and into the continuation phrase – the Scriabin example, however, makes use of a surrogate harmony during the prolongation – that is followed by fragmentation and a cadence in the continuation phrase.
Example 8 is taken from the beginning of Chopin’s Prelude, Op. 28, No. 13 in F♯ major (1838/39). Just like the previous two examples, the presentation may be broken down into two-measure units, a basic idea that is repeated.41 Chopin creates a static melody in the opening phrase, and the interest for the listener lies in the surface-level rhythmic activity of the left hand and the pervasive usage of a double-neighbour pattern. In addition, just as with the previous two examples, the tonic is prolonged throughout the presentation phrase. The first important deviation from the paradigm discussed thus far occurs in the continuation phrase. Here, no fragmentation of the phrase structure is present; instead, Chopin creates a seamless gesture that leads to a cadence. Specifically, the static melody of the presentation phrase is abandoned as the F♯ major triad is outlined moving from A4 to F♯5 in an ascending gesture followed by a descending, stepwise line to C♯5; specifically, a melodic line moving from fa to do is supported by ii to V7 to I that is part of a dominant tonicization.

Caplin conjectures that there is an alternative design used in the continuation phrase, which he refers to as continuation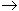 cadence. As he explains,
cadence. As he explains,
the decision to call the second half of a sentence a continuation phrase reflects the fact that, in the majority of cases, continuation function is more prominently displayed than cadential function is … In some cases, however, the cadential component vies for equal expression with the continuation function, or even surpasses it. Cadential function acquires this greater status when the phrase begins directly with the cadential progression, which is then expanded to support the entire phrase.42
As stated previously the seamless melodic line in the second phrase of Example 8 is supported by a coherent and unmistakable cadential progression that stands in stark contrast to the phrase-structure fragmentation observed in the both the Tchaikovsky and Scriabin examples.43 It is also important to note that it is likewise distinct from the consequent phrase of a period because, in the latter, the basic idea of the antecedent phrase is restated and then followed by a contrasting idea.44 The final point of interest in the continuation phrase in Example 8 is its irregular length. Both of the two previous examples had a clear 4 + 4 phrase structure in the sentence, whereas the Chopin example has a 4 + 3 phrase structure: the fourth measure of the second phrase is devoted to a bridge that connects the end of the first sentence to the beginning of the next sentence (that is not shown in Example 8). Chopin creates a walking bass line that re-introduces B♮ in preparation for a restatement of the F♯ tonic.
Having reviewed other examples of a sentence with the students is helpful. First, it will reinforce Caplin’s paradigm of the sentence, which can be confusing for students, especially when compared to the period. However, by discussing three examples of a presentation phrase that prolong a single harmony, the tonic, and that do not subsequently culminate in a cadence, it can be clearly distinguished from the antecedent phrase of a period and its constituent basic idea and contrasting idea. Furthermore, by invoking the concept of enjambment from poetry, the student is made aware that the ear of the listener is guided immediately to the continuation phrase. By contrast, the rhetorical pause at the end of the antecedent phrase – that is achieved via a cadence – is markedly different. Second, the two types of continuation phrases that Caplin discusses (with or without fragmentation) demonstrate how the underlying syntax is brought to completion.45 Third, by using examples from the Romantic period, Scriabin’s preludes can be contextualized within the milieu from which his own work drew inspiration. As stated at the beginning of the paper, while his harmonic palette becomes increasingly more complex than his Romantic predecessors, his use of phrase structure remains traditional and constitutes a link to the past.
Thus primed, the students are now ready to look at the original Scriabin excerpt. The opening eight measures of the prelude are shown again in Example 9, and the labels used in the previous examples are employed to evince a sentence that is comprised of a 4 + 4 phrase structure. Just as with the other three examples, a single harmony is prolonged throughout the presentation phrase. What is unique here is how the basic idea is repeated, which results in a greater aural sense of departure from the home key until the arrival of the root-position tonic harmony at m.4 (which itself may also be heard as a dominant)46. In preparation for this discussion, the students are asked to write down the three ways in which the basic idea may be repeated: exact, statement/response, & sequential. I then play the opening four measures of the prelude while half the class sings the melody and the other half sings the bass line. The student groups, formed earlier, are then asked to confer about which method is used here, and the preparatory work done initially (i.e., when the students were asked to identify patterns) comes to fruition. The students identify the third method, sequential, which is identified accordingly in the analysis.

Regarding the continuation phrase, it resembles the Chopin passage presented in the Example 8. Scriabin similarly creates a seamless melodic line: it begins with a descending, stepwise line from F4 to B3, outlining a tritone, and concludes with an ascending leap to G4. In addition, this melodic line is supported by a prolongation of the Neapolitan moving to the dominant harmony at the cadence. Unlike the Chopin example, the sentence identified in Example 9 shows how Scriabin uses a symmetrical 4 + 4 phrase structure (he most often uses a regular phrase structure in these preludes). The remainder of Scriabin’s work will be addressed in the next section that examines the post-tonal elements.
Scriabin, Prelude, Op. 31, No. 4: Creating a Non-Traditional Harmonic Palette with Whole-Tone Elements
I turn now to other features of the prelude that are best construed in a post-tonal frame of reference. Example 10 shows the opening melody of the prelude, senza anacrusis, where each note has been identified as an integer. The parenthesized notes are used to depict elements of the melody that are used for diminution (e.g., the C4 at the end is a dissonance that is part of a 4-3 appoggiatura figure). The students are asked to sing through the melody, stemmed notes only, on a neutral syllable (I can say, without exception, that students are always surprised and elated to hear the whole-tone scale Scriabin has embedded in the melody). Next, I ask the students to write in integers above the important notes in the melody, after Example 10, and to re-sing the melody using the syllables based on the integers.47
Once the students are aware that there is a whole-tone, melodic component to the prelude, the next task is to decide if Scriabin also used this collection as inspiration for some of the underlying harmonies. To begin, I return to the chord at the anacrusis, see Example 4d, and ask the students to annotate the score by converting each note to an integer where C = 0. They quickly see that all four notes, or pcs, are odd numbers. Students are then asked to sing the content of the tetrachord first in ascending order {137e} and then in normal order {e137}.48 Once the normal order has been established by the students, continuing to work in groups, they are asked to determine the set class to which pc set {e137} belongs, which is Forte sc 4-24.49 Students are then encouraged to find other harmonies of either cardinality 3 or 4 that are subsets the whole-tone collection.50
Next, it is useful to contextualize how Scriabin uses the post-tonal elements, that is to say, to place it in a continuum of practice. At one end, there is the use of whole-tone elements in juxtaposition to tonal elements. Example 11a shows a passage from Debussy’s “Beau soir” (1877/78). The prevailing tonality used by the young composer is E major that is prolonged via a ♭VI harmony; however, the submediant has an altered fifth so that it is an augmented chord – a subset of the whole-tone collection.51 In addition, a whole-tone pentachord is present in the melodic dimension. Truly, Debussy’s use of the collection adds a soupçon of whole-tone seasoning that is momentarily juxtaposed against E major.
At the other end of the continuum, there is the exclusive use of whole-tone elements with only a fleeting reference to a tonal context.52 Example 11b shows an excerpt from Berg’s “Schlafend trägt man mich” (1909/10). Here, in the piano interlude, Berg alternates between the two whole-tone collections: he uses a WT0 pentachord on the downbeat of each measure – followed by a subset from WT1 – that is successively transposed up a whole step.53 Indeed, the T2 operation at work can be conceived as a type of word painting that conveys the journey of the narrator (“from afar I come, over peaks, over abysses…”). The result of the alternation between the two collections is that, in the melodic dimension, there are chromatic elements (see, for instance, 3-2 {346} in the right-hand melody of m. 3). Unlike the Debussy example, a sense of a prevailing tonality is clouded by the whole-tone elements. As a consequence, the present Scriabin prelude falls in the middle of this continuum; the listener neither hears the juxtaposition of a whole-tone collection with a diatonic collection nor does the listener hear the exclusive utilization of whole-tone elements. Instead, the artistry of Scriabin’s transitional work is appreciated by the listener in hearing music infused with whole-tone elements that ultimately enrich the harmonic palette while never undermining the prevailing tonality – integration rather than juxtaposition or exclusivity.
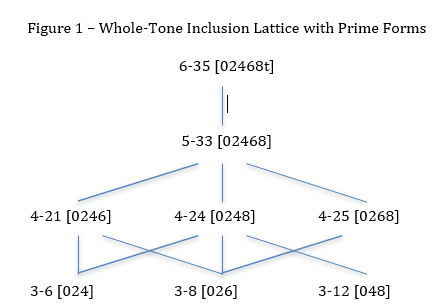
Returning to the post-tonal analysis of the fourth prelude, a discussion of all the possible subsets of the whole-tone collection will help the students to identify the underlying harmonies that may be present. Figure 1 shows an inclusion lattice for the whole-tone collection.54 A quick look at the lattice shows students that there is just one subset of cardinality 5, three subsets of cardinality 4 and three subsets of cardinality 3.55 The students will have a clear sense for which sonorities they should be searching (specifically, a list of 29 tetrachords has been reduced to three).56 Moreover, the lattice shows relationships between subsets; for instance, sc 3-8 is a subset of all three of the tetrachords listed whereas sc 3-12, the augmented triad, is a subset of only one of the tetrachords listed. Thus, in addition to reviewing familial relationships amongst set classes of different cardinalities, students will also be introduced to inherent compositional implications.57
After giving the students groups some time to do their segmentation (ideally as a collaborative homework assignment), it is time to review the results. Example 12 shows the likely result of this endeavour.58 Curiously, there is just one occurrence of sc 4-21, which will be addressed in an analysis of the final phrase. Importantly, Scriabin alters the bass line pattern in the presentation phrase of the second sentence so that the G3 – D3 – F3 – C3 in the opening phrase is transformed to G3 – D♭3 – F3 – B2 (compare 1–4 and 9–12 in Example 12), and the perfect fourth is replaced with the tritone. Thus the V/V chord that is found at the end of m.2 has now been transformed to a whole-tone harmony in m. 10, sc 3-8 (the Italian augmented-sixth chord); however, in this context, rather than acting as a conduit to a dominant chord – the traditional syntactical role of pre-dominant – the harmony is itself a goal. By implication then, does it too assume the role of a back-relating dominant to the G major harmony that precedes it? I play the two chords in reverse order on the piano and ask the students for their opinions.
Perhaps most significantly, the revised bass line in mm. 9–12 is itself an instance of sc 4-25, and the content of pc-set {57e1} is identical to the vertical sonority that occurs at the end of m. 1.59 This analytical discovery provides the perfect opportunity to discuss Schoenberg’s notions about the equivalency of the horizontal and the vertical:
A musical idea, accordingly, though consisting of melody, rhythm, and harmony, is neither the one nor the other alone, but all three together. The elements of a musical idea are partly incorporated in the horizontal plane as successive sounds, and partly in the vertical plane as simultaneous sounds. The mutual relation of tones
regulates the succession of intervals as well as their association into harmonies … And this explains why, … a basic set of twelve tones (BS) can be used in either dimension, as whole or in parts.60
While Schoenberg is presenting his ideas on the twelve-tone technique, the interchangeability of the melodic with the harmonic (a phenomenon that Schoenberg would argue has its roots in the tonal repertoire) is also pertinent to other twentieth-century literature. The relationship between the vertical chord at the end of the first measure and the transformed bass line in mm. 9–12 provides a vibrant example.
Hence, the analysis in Example 12 unequivocally demonstrates that Scriabin has infused the tonal environment with whole-tone elements, both melodic and harmonic. What is of particular interest is that each of the harmonies identified is a literal subset of WT1 – thought of in a more musical context, each of the underlying harmonies was harvested from the melody shown in Example 10. Furthermore, the analysis can be thought of in two ways if we accept Schoenberg’s premise of the equivalency of the horizontal and the vertical: not only are these underlying harmonies harvested from the whole-tone scale embedded in the melody, these underlying harmonies also cumulatively generate the whole-tone collection.61 Concerning the interaction of the whole-tone elements in a tonal environment, James Baker comments “we have seen that prolongations of tonal functions or progressions often form whole-tone aggregates. These whole-tone collections never take structural precedence over the tonal gestures, but it is remarkable that the two procedures are not mutually exclusive.”62 Indeed, most students are aurally unaware of the whole-tone component of the prelude until completing a pc-set analysis – a testament to Scriabin’s skill at crafting a piece in which tonal and post-tonal elements achieve a symbiosis; subsequently, many students will confess that the whole-tone elements are more apparent when listening to the prelude post-analysis.63
Scriabin, Prelude, Op. 31, No. 4: Combining Traditional & Non-Traditional Features in the Formal Design64
Finally, I address the final phrase of the prelude, which is shown in Example 13. The sonority at the beginning of m. 12 – the end of the first phrase of the second sentence – belongs to sc 4-21 and, as just discussed, represents another subset of the whole-tone collection. But, as has also been mentioned, these whole-tone chords are presented in a prevailing, tonal environment. Thus, is there a way to contextualize this chord in a tonal progression? A brief comparison of mm. 13–18 in Example 13 with mm. 4–8 in Example 9 shows two continuation phrases that culminate in a cadence; in the case of Example 13, the phrase culminates in a perfect, authentic cadence. Given the similarity of the conclusion of these two phrases, I will focus my attention on the very beginning of the continuation phrase in the second sentence that occurs at the pick-up to m. 13.
Once again, there is a first-inversion submediant harmony, which acts as a surrogate for the tonic. In terms of the underlying syntax, I have identified the harmony as a tonic substitute (TS) – in the analysis, the roman numeral “I” in quotation marks means that the harmony is acting as a “quasi-tonic.” Moving back to the whole-tone harmony at the end of the presentation phrase – located on the downbeat of m. 12 – it can likewise be understood as a surrogate, specifically, as a “quasi-dominant.” Indeed, one could conceptualize this chord as a dominant-eleventh chord with an omitted root, raised fifth, and raised eleventh: (G) – B – D♯ – (F) – A – C♯. While there are treatises that discuss the possibility of an omitted root, students are skeptical when considering chords with no sounding fundamental.
To compensate, students are more receptive when introduced to the work of Varvara Dernova. In a nutshell, she posits that Scriabin conceptualized a major-ninth chord that is referred to as a whole-tone chord: G (pc 7) to B (pc e) to a lowered fifth D♭ (pc 1) to a raised fifth D♯ (pc 3) to F (pc 5) to A (pc 9).65 Dernova also makes clear that this sonority is enharmonically related to all of its inversions (which is another way of stating that one is dealing with a symmetrical set). For instance, the same chord starting a major third higher is: B (pc e) to D♯ (pc 3) to a lowered fifth F (pc 5) to a raised fifth F![]() (pc 7) to A (pc 9) to C♯ (pc1).66 Thus, this context provides another theoretical foundation on which to assert that the tetrachord in m. 12, sc 4-21, is a quasi-dominant: it represents a major-ninth chord, built on B, in which both altered fifths have been omitted. The conversation has once again become dense, just like the earlier discussion about augmented-sixth chords. Consequently, the instructor is similarly encouraged to include only that material that is appropriate to the skill level of the students and to the content of the lesson plan (Dernova’s esoteric musings on the whole-tone chord can be included or not).
(pc 7) to A (pc 9) to C♯ (pc1).66 Thus, this context provides another theoretical foundation on which to assert that the tetrachord in m. 12, sc 4-21, is a quasi-dominant: it represents a major-ninth chord, built on B, in which both altered fifths have been omitted. The conversation has once again become dense, just like the earlier discussion about augmented-sixth chords. Consequently, the instructor is similarly encouraged to include only that material that is appropriate to the skill level of the students and to the content of the lesson plan (Dernova’s esoteric musings on the whole-tone chord can be included or not).
In terms of the voice leading, the major second between B and C♯ is better thought of as an enharmonically respelled diminished third because it contracts inwards to a unison as shown in Example 14.67 In this progression, there is a single common tone while all of the other notes move by semitone. I believe the clincher for asserting the syntactical role of a dominant substitute for this sonority lies in how the major second – the basic building block of all whole-tone sets – is treated like the diminished third of an augmented-sixth chord. It is also significant that this is the one and only place where sc 4-21 makes an appearance (previously, the tetrachordal sets used by Scriabin have been restricted to sc 4-24 and sc 4-25).68 It is the voice-leading potential that makes this unique chord so profound and indispensable.
There is one conspicuous feature in the analysis of Example 13 that has not been addressed: Why place a grand pause right before the arrival of the final cadence? To answer this question, it is necessary to review Scriabin’s spiritual inclinations. The Theosophical Society, founded in New York in 1875, and its well-known guru Helena Blavatsky experienced a period of growth in popularity during the 1890s and early 1900s. Scriabin was influenced by this movement from the days of writing the Divine Poem onwards.69 Furthermore, the number seven has a very important meaning in Theosophy (e.g., the Theosophical emblem has seven elements, Blavatsky taught that there were seven planes of existence, a sevenfold nature of man, etc.)70 Scriabin’s final and unfinished composition, the Mysterium (which he began composing in 1903, the same year as the present prelude), is a spiritual manifesto of sorts, and the number seven is prominent. Scriabin explains that the “Mysterium is a living act for all, all mankind, universal in concept, and not just a fancy in my head.”71 The piece was to be performed over a period of seven days after which reality would dissolve and mankind would be transformed to a plane of unity. Intriguingly, the grand pause in the prelude occurs exactly in the seventh measure of the second sentence.72 Thus, the completion or fulfillment of the prelude occurs after the seventh measure, a measure of silence; as a result, this work may be seen as a microcosm of the Mysterium.
In terms of the formal design, the prelude is a one-part form that is comprised of a period, specifically, a modified 16-measure period.73 As seen in Figure 2, the first sentence, mm. 1–8, is now understood as the antecedent phrase at this meta level, which is punctuated by a half cadence. Similarly, the second sentence, mm. 9–18, is understood as the consequent phrase, which is punctuated by a perfect authentic cadence. This design is conventional because preludes are often one-part forms made up of a tightly-knit organization such as a sentence or a period.74 Mathes asserts that “in tonal music, the most salient feature of one-part forms is continuous harmonic motion such that a conclusive cadence in the tonic key is not heard until the end of the piece.”75 A “conclusive cadence in the tonic” appearing only at the end is certainly evident here, and it is further emphasized by the grand pause in m. 7 of the second sentence or consequent phrase at the meta level. Accordingly, I offer a counterargument to commentators such as Hull and Taruskin who argue for Scriabin as a composer of absolute music. The extra-musical underpinning of Theosophy provides a narrative that helps the listener comprehend the asymmetrical design of the prelude.76
This study of Scriabin’s prelude has allowed us to observe the concurrence of a tonal idiom (evinced in the harmonic analyses) with the whole-tone collection (evinced in the pc-set analyses). It has also allowed us to see that the phrase structure and formal design of the common-practice period continue to be used by Scriabin to organize his evolving harmonic palette (certainly, the underlying syntax of the examples from his oeuvre has much in common with the music of the past). As a result, the narrative of rupture often used in connection with Scriabin and composers of his ilk is deemed to be imprecise. James Baker states: “I believe strongly that Scriabin’s transition from tonality to atonality can best be studied in terms of specific alterations and modifications which he introduced into the traditional tonal system.”77 This composition from the beginning of his middle period provides an ideal opportunity to observe this transition and thereby allow our students the benefit of a multi-faceted approach to analysis.
Bibliography
Aldwell, Edward and Carl Schachter. Harmony & Voice Leading, 4th ed. Boston: Schirmer, Cengage Learning, 2011.
Baker, James. “Scriabin’s Implicit Tonality.” Music Theory Spectrum, Vol. 2 (spring 1980): 1-18.
____________. The Music of Alexander Scriabin. New Haven, Connecticut: Yale University Press, 1986.
Bower, Faubion. The New Scriabin: Enigma and Answers. New York: St. Martin’s Press, 1973.
Bribitzer-Stull, Matthew. “Contention in the Classroom: Encouraging Debate and Alternate Readings in the Undergraduate Theory Class.” Journal of Music Theory Pedagogy, Vol. 17 (2003): 21-45.
Caplin, William. Classical Form: A Theory of Formal Functions for the Instrumental Music of Haydn, Mozart, and Beethoven. New York: Oxford University Press, 1998.
_____________. Analyzing Classical Form: an Approach for the Classroom. New York: Oxford University Press, 2013.
Clague, Mark, Julie Evans, Karen Fournier, Maud Hickey and Betty Anne Younker. “Building Bridges: Same and Different Issues Across Music Theory, Music History, and Music Education.” College Music Symposium, Vol. 49/50 (2009/2010): 140-53.
Clendinning, Jane Piper and Elizabeth West Marvin. Theory and Analysis, 3rd ed. New York: W.W. Norton & Company, 2016.
Dirkse, Scott. “Effective Questioning Strategies for the Music Theory Classroom,” Journal of Music Theory Pedagogy, Vol. 28 (2014): 69-84.
Forrest, David and Matthew Santa. “A Taxonomy of Sentence Structures.”College Music Symposium Vol. 54 (August 2014).
Friedmann, Michael. Ear Training for Twentieth-Century Music. New Haven, Connecticut: Yale University Press, 1990.
Gauldin, Robert. Harmonic Practice in Tonal Music, 2nd ed. New York: W.W. Norton & Company, 2004.
Guenther, Roy James. “Varvara Dernova’s Garmoniia Skriabiana: a Translation and Critical Commentary. PhD diss., The Catholic University of America, 1979.
Harrison, Daniel. “Supplement to the Theory of Augmented-Sixth Chords.” Music Theory Spectrum, Vol. 17, No. 2 (Autumn 1995): 170-95.
Hasty, Christopher. “Segmentation and Process in Post-Tonal Music.” Music Theory Spectrum, Vol. 3 (spring 1981): 54-73.
Hull, A. Eaglefield. Modern Harmony: its Explanation and Application. Boston: Augener Ltd., 1915.
____________. “A Survey of the Pianoforte Works of Scriabin.” The Musical Quarterly, Vol. 2, No. 4 (October 1916): 601-614.
Kleppinger, Stanley V. “Strategies for Introducing Pitch-Class Set Theory in the Undergraduate Classroom.” Music Theory Pedagogy Online, Vol. 24 (2010): 131-156.
Laitz, Steven. The Complete Musician: an Integrated Approach to Tonal Theory, Analysis & Listening, 4th ed. New York: Oxford University Press, 2016.
Mathes, James. The Analysis of Musical Form. Upper Saddle River, New Jersey: Pearson, 2007.
Mead, Andrew. “Shedding Scales, Understanding Intervals in Different Musical Contexts.” Theory and Practice, Vol. 22/23 (1997-98): 73-94.
Reddick, Carrisa. “Teaching Analysis of Chromatic Chords through Chord Qualities.” Music Theory Pedagogy Online, Vol. 2 (2013): 1-37.
Rogers, Nancy and Robert W. Ottman. Music for Sight Singing, 9th ed. Upper Saddle River, New Jersey: Pearson, 2014.
Roig-Francolí, Miguel. Understanding Post-Tonal Music. New York: McGraw-Hill, 2007.
Salzer, Felix and Carl Schachter. Counterpoint in Composition: the Study of Voice Leading. New York: Columbia University Press, 1969.
Schoenberg, Arnold. “Composition with Twelve Tones (I),” in Style & Idea: the Selected Writings of Arnold Schoenberg, ed. Leonard Stein, trans. Leo Black. Los Angeles: University of California Press, 1975.
Schuijer, Michiel. Analyzing Atonal Music: Pitch-Class Set Theory and Its Contexts. Rochester, New York: University of Rochester Press, 2008.
Straus, Joseph N. Introduction to Post-Tonal Theory, 4th ed. New York: W.W. Norton & Company, 2016.
Swan, Alfred J. Scriabin. New York: Da Capo Press, 1923.
Taruskin, Richard. “Review of The Music of Alexander Scriabin.” Music Theory Spectrum, Vol. 10 (spring 1988): 143-169.
____________. “Scriabin and the Superhuman,” in Defining Russia Musically. Princeton, New Jersey: Princeton University Press, 1997.
Appendix I

Appendix II
I use in this paper the syntactical labels adopted by Robert Gauldin’s, Harmonic Practice in Tonal Music, 2nd ed. (New York: W.W. Norton & Company, 2004), Jane Piper Clendinning & Elizabeth West Marvin’s Theory and Analysis, 3rd ed., (New York: W.W. Norton, 2016), and Steven Laitz’ The Complete Musician, 4th ed., (New York: Oxford University Press, 2016) where T = Tonic, PD = Pre-Dominant, & D = Dominant.78 It must also be stated that these labels are placed immediately beneath a roman-numeral/figured bass analysis in order that the latter may be contextualized. The influential textbook, Aldwell & Schachter’s Harmony & Voice Leading – that was first published in 1978 – includes an excellent discussion on harmonic syntax and introduces similar labels: T = Tonic, Int = Intermediate Harmony (a harmony the precedes the dominant), & D = Dominant. These authors deliberately avoid using the term “function” – neither this term nor “harmonic function” is found in the subject index – and instead encourage the use of these labels to help the student “organize chords into broader classes and serve as a ‘litmus’ test to determine whether a progression of chords conforms to a proper harmonic syntax.” Aldwell and Schachter, Harmony & Voice Leading, 175 (see also 204-05).
No doubt, this omission stems from a desire to refrain from invoking Hugo Riemann’s notions about functional harmony. Interestingly, the term “harmonic syntax,” or just “syntax,” does not appear in the subject index of any of the three textbooks listed above. Gauldin introduces these labels in a section on “harmonic tendency,” and he suggests that “roman numerals provide us with a useful means for expressing harmonic tendency, assuming we know their tonic, dominant, and pre-dominant character … it is the musical context that ultimately determines the harmonic function of chords.” Gauldin, Harmonic Practice, 123. The Clendinning/Marvin textbook uses these labels in a discussion about the phrase model – implicitly invoking an understanding of harmonic syntax. Clendinning/Marvin, Theory and Analysis, 261. Laitz introduces these labels in a discussion of “function,” and he describes the intermediate harmonies of a tonal progression as follows: “[the progression] contains independent sonorities that act as connective tissue between the tonic and the dominant. We call these chords pre-dominant because they precede the dominant.” Laitz, The Complete Musician, 264. Thus, while Laitz’ useful description of an intermediate harmony, or pre-dominant, is clearly in line with Aldwell & Schachter’s definition, the three categories of harmonic organization, which Laitz calls “three functions,” might be seen as conflating Riemann’s ideas about functional harmony with Schenker’s ideas about Stufe or scale degrees. As Caplin explains, “In Riemann’s Funktionstheorie, subdominant function is primarily conceived (following Rameau) as one of two tonal poles to the tonic … the North American adaptation of the functional theory, which emphasizes a group of pre-dominant harmonies leading to the dominant, has most likely been influenced in this respect by Schenkerian notions.” Caplin, Classical Form, 262 (f.n.5). Brian Hyer makes an additional distinction about function theory: “in contrast to scale-degree theories, function theories are concerned more with harmonic identities than with chord progressions.” Brian Hyer, “Tonality,” in The Cambridge History of Western Music Theory, ed. Thomas Christensen (New York: Cambridge University Press, 2002), 736. Consequently, the instructor must be patently clear in the lesson plan how the word “function,” if adopted, will be explained to, and used by, the students.
Notes
1 The examples provided in this discussion can be used in a two-year program that, of necessity, addresses the 20th-Century repertoire in a perfunctory manner and cannot dedicate time to longer pieces. Additional suggestions for exercises are provided for instructors who wish to dedicate more time to this subject material.
2 The situation is analogous to the out-dated way in which a working model of the atom is often still presented; namely, an elaborate simile that likens the electron to a planet orbiting about a sun/nucleus. No doubt, the convenience of a solar-system model is a handy default that obviates the more complex and necessary discussion about probability clouds in connection to the electron. Similarly, the model of rupture that still persists in connection to the repertoire of the early twentieth century also entertains convenience at the expense of a more comprehensive understanding.
3 A. Eaglefield Hull, “A Survey of the Pianoforte Works of Scriabin,” The Musical Quarterly, Vol. 2, No. 4 (October 1916): 605. A copy of the score for the fourth prelude is found in Appendix I.
4 Hull delimits Scriabin’s oeuvre thus: the first period, Op. 1 – 18, the second period, Op. 19 (the Second Sonata) – 49, and the third period, Op. 51 – 74. Hull, “A Survey,” 602. By contrast, James Baker places the beginning of the second period, what he terms the “transitional period,” and the third period, what he terms the “atonal period,” at later dates: the early period up to 1903, the transitional period from 1903 (specifically, the Divine Poem, Op. 43) to 1910, and the atonal period from 1911 (specifically, Prometheus: the Poem of Fire, Op. 60) to 1915. James Baker, The Music of Alexander Scriabin, (New Haven, Connecticut: Yale University Press, 1986), vii & 145.
5 Before singing, it is helpful to quiz the students on the syllables used for the lowered scale degrees (specifically, te, le, me and ra). In addition, depending on the skill level of the class, it might first be beneficial to require the students to sing a descending C major scale and then to sing the descending form of the c minor melodic scale that also includes ra and ti for a cadence, specifically do – te – le – sol – fa – me – ra – ti – do. Next, the students are asked to sing only those notes of the melody that fall on the downbeat of each measure, including the initial do on the upbeat, which will result in a hybrid of the descending C major scale, from do to sol, and the descending form of the c minor scale, from sol to do. Lastly, the students are asked to sing the entirety of the melody.
6 A thorough review of effective questioning goes beyond the scope of this paper; for a helpful resource, see Scott Dirkse, “Effective Questioning Strategies for the Music Theory Classroom,” Journal of Music Theory Pedagogy, Vol. 28 (2014): 69-84. Regarding the group work, this strategy adheres to Dirkse’s first characteristic of effective questioning, which states that “questions should be directed to all students,” the fourth characteristic, which states that “questions should be inviting, not intimidating,” (students feel safer sharing their thoughts with colleagues in an intimate, collaborative setting), the fifth characteristic, which states that “questions should require student thinking,” and the sixth characteristic, which states that “questions should elicit maximum student participation.” Ibid., 71, 74, 75 & 76.
7 The instructor is encouraged to create a list of initial questions that will benefit the lesson plan, and the questions presented here are not intended to be exhaustive. Moreover, a question about rhythm has not been included because, as mentioned previously, the chorale-style setting does not lend itself to rhythmic intricacy. That being said, the initial dotted rhythm at the beginning of each two-measure unit and the slow tempo are reminiscent of a French Overture, which is a stylistic consideration.
8 On occasion, some students have indicated E♭ major (no doubt this conclusion is reached in reference to the E♭s that occur: see the anacrusis, the applied chord in m. 4, and, most notably, the ♭III chord in m. 6 – the discussion of the voice-leading function of this chord to follow will help guide these students). Students who tend to rely solely on a visual experience of the piece via the score may be perplexed by Scriabin’s use of accidentals; referring these students back to their auditory experience of the harmonies that fall on the downbeats and the two cadences (half cadence on G and authentic cadence on C) will help them comprehend the prevailing tonality. In reference to recordings of this work, the key of this prelude is sometimes listed as A♭ major. Specifically, I contacted the Hyperion label about a recording by Piers Lane (The Complete Preludes, Vol. 2 – CDH55451) for which the errant key is listed. Given that I have not come across a different version in the literature, that there is no scholarly disagreement about the key itself, and that the recording in question is indeed in C major, I speculated that this prelude might have been conflated with Op. 33, No. 4 when it was catalogued. The copyright and licensing manager from Hyperion confirmed that such was the case in an email dated September 27, 2016; the database will be updated accordingly. An inquiry was also dispatched to Naxos, but a response was never received.
9 In preparation for this piece, at the previous class I provide the following bass line for the students to harmonize: C3 – F3 – D3 – G3 – E3. I explain that they should realize a functional progression in C major that may make use of an applied chord where appropriate. The progression the students typically generate is I to IV, or ii6, to ii, or V/V or V7/V, to V to I6 (the progression ends with an evaded cadence – an F3 passing note is often inserted between G3 and E3 in the literature; in addition, the cross relation that results between IV or ii6 and the applied chord must be treated carefully). After analyzing the first eight measures of the prelude, the students are asked to compare the bass line they were required to harmonize with the bass line in the prelude. They are surprised/delighted to see that Scriabin uses the retrograde form of this conventional progression in the opening four measures.
1010. Regarding the ♭VI harmony, it is labelled as an applied chord in the analysis. The reason behind this choice is that it is presented in first inversion where the bass note is approached via common tone and moves by half step to the root of the Neapolitan chord that follows. The sonority sounds like an inverted dominant guiding the ear to the important pre-dominant chord that follows to my ear. This analytical choice also explains why the analysis in A♭ major is so brief – it hints at a possibility that is discarded in favour of a cadential progression in the home key. Without a doubt, the progression from the D♭ major harmony in m. 5 to the E♭ major harmony in m. 6 could be construed as a PD to D progression in A♭ major; however, the E♭ major harmony, or ♭III in relation to the home key, is not a structural dominant but a voice-leading chord that facilitates a voice exchange and a prolongation of the Neapolitan chord.
11 The pattern in the bass voice may also be identified as up a third/down a fourth by taking into account the anacrusis. If the students are focusing on downbeats, this distinction may not be immediately apparent.
12 This passage may inspire a review of the distinction between a tonicization and a modulation – a subtle and perplexing distinction for many students. In the present example, it is beneficial to refer students back to their aural experience of the opening phrase. Do they hear a fundamental shift to the key of the subtonic? Does the analysis reveal an authentic cadence in this new key? If the answer to these questions is “no” then a tonicization is the appropriate interpretation – specifically a tonicization within a sequential pattern – rather than a full-fledged modulation.
13 Given the Largo tempo marking, it is possible to utilize William Caplin’s notion about real versus notated measures: in this instance, it is a very slow tempo marking where R = ½ N, or one real measure (R) is equivalent to one half of a notated measure (N). Therefore, the literal measures shown in Example 2 are understood to be four measures, and the correlation between the Chopin excerpt and the first four measures of the Scriabin prelude is even more compelling. A detailed explanation of Caplin’s notion can be found in his Classical Form (New York: Oxford University Press, 1998), 35.
14 This example provides an excellent opportunity to reinforce that the purpose of a harmonic analysis is not restricted to identifying chordal spellings and qualities; rather, it is a tool that also helps to identify patterns and to interpret the underlying harmonic syntax.
15 The concept of the back-relating dominant is discussed in Edward Aldwell and Carl Schachter, Harmony & Voice Leading, 4th ed. (Boston: Schirmer, Cengage Learning, 2011), 189, and Steven Laitz The Complete Musician, 4th ed. (New York: Oxford University Press, 2016), 372-74.
16 While the counterpoint in the final measure is not technically fourth species – there is no preparation of the dissonant fourth above the bass – it is a type of appoggiatura that students are encouraged to include in post-sixteenth-century, tonal, fourth-species counterpoint. It may be thought of as an unprepared suspension – coined from the Oxford Music Online – that still resolves down by step. Interestingly, had Scriabin used the 6-5 technique in the previous measure, this dissonance would have been prepared. Thus, more precisely, given that Scriabin omits the second half of the 6-5 motion and uses first-species counterpoint, the dissonance in the final measure is the result of a contraction. Felix Salzer and Carl Schachter, Counterpoint in Composition: the Study of Voice Leading (New York: Columbia University Press, 1969), 178. Students are also asked to place a box around dissonances when they compose a counterpoint that includes dissonances or when they devise a voice-leading schema; in this way, they are prompted to discern how the dissonance is both approached and resolved.
17 For a complete explanation of the syntactical labels used, please see Appendix II.
18 When discussing the possible voicings of the augmented-sixth chord, the term configuration is most apt because it avoids the fallacious usage of the term inversion, which should only be used with sonorities that can be demonstrated to have a chordal root.
19 One can literally see that me, or B♭, at the end of the triplet on the first pulse has been respelled as ri, or A♯, on the third pulse. This can also be understood as an enharmonically reinterpreted harmony, which is depicted in the analysis by the V4/3 label.
20 Daniel Harrison discusses this possibility and determines twelve (12) potential classes of resolution of the four augmented-sixth pairings in the major mode. Daniel Harrison, “Supplement to the Theory of Augmented-Sixth Chords,” Music Theory Spectrum, Vol. 17, No. 2 (Autumn 1995): 174. According to Harrison’s nomenclature, the augmented-sixth chord in letter b is understood to have a “plagal” functional type. Harrison, “Supplement,” 187. His Figure 4 provides two broad categories of augmented-sixth chords based on privileging two sets of constituent dyads: ♭![]() &
& ![]() are considered dominants because these tendency tones are understood to resolve exclusively to the root of I, and not, say, the fifth of IV, and ♭
are considered dominants because these tendency tones are understood to resolve exclusively to the root of I, and not, say, the fifth of IV, and ♭![]() & ♯
& ♯![]() are considered subdominants because these tendency tones are understood to resolve either to the root of V or to the fifth I. Ibid., 187. Thus, when the tendency tones of the subdominant type resolve to the tonic, the progression is dubbed a plagal (subdominant to tonic) functional type.
are considered subdominants because these tendency tones are understood to resolve either to the root of V or to the fifth I. Ibid., 187. Thus, when the tendency tones of the subdominant type resolve to the tonic, the progression is dubbed a plagal (subdominant to tonic) functional type.
21Harrison discusses the peculiarity of the dominant-function, augmented-sixth chord in the literature (he provides a pertinent example from Liszt’s Orpheus), and a reluctance to discuss it in contemporary harmony textbooks. Harrison, “Supplement,” 178-79 (regarding textbooks, see f.n. 22). Since the article was published, there are two additional textbooks, not addressed by Harrison, that have become widely used: Theory and Analysis, 3rd ed. by Clendinning & Marvin (New York: W.W. Norton, 2016) and The Complete Musician, 4th ed. by Laitz. In the former textbook, dominant-function augmented-sixth chords are referred to as “secondary” augmented-sixth chords and the student is exhorted to label it as an applied chord of the tonic or Gr6/i (the example cited is an excerpt from Schubert’s “Der Doppelgänger” from the Schwanengesang – see p. 566). The discussion is restricted to a single paragraph, accompanied by the Schubert example, and is located at the end of the chapter; lastly, in the summary box that concludes the chapter, the following bullet point precludes the “secondary” function just presented: “they [augmented-sixth chords] are pre-dominant chords that intensify motion to V through chromaticism.” In the latter textbook, a discussion of the augmented-sixth chord appears in two chapters. In Chapter 24, “The Augmented Sixth Chord,” in addition to the standard review of the types of augmented-sixth chord, there is commentary on the usage of the augmented-sixth chord in pre-dominant expansions, and the chapter concludes by discussing its usage as a pivot chord via enharmonic reinterpretation. The second chapter in which it appears is Chapter 28, “New Harmonic Tendencies,” which provides an excellent tutorial on the common-tone, augmented-sixth chord (see pp. 690-91). In the previous 3rd ed., this topic included an, “Analytical Interlude” – see Chapter 29, “The Rise of Symmetrical Harmony in Tonal Music” – which has sadly been omitted from the 4th ed. (no doubt at the behest of the editor). Laitz discussed an excerpt from Wolf’s “Man sagt mir, deine Mutter woll’ es nicht” from the Italienisches Liederbuch (see pp. 618-20, 3rd ed.). He points out an “altered” augmented sixth chord (one identical in spelling to Scriabin’s anacrusis chord in Example 4d whereby mi, spelled as a diminished fourth, is used instead of me) that leads directly to an F♯ tonic harmony. Curiously, Laitz’ insightful commentary reflects on the sudden shift from a minor to F♯ major and its text-setting implication, but a discussion on the syntactical role of this chord must be inferred from the analysis. To be sure, a reluctance to address this topic comprehensively, rather than tangentially, appears to persist in the contemporary textbook.
22 ♯![]() , or ri, could have been used in this vertical sonority as well, but ♭
, or ri, could have been used in this vertical sonority as well, but ♭![]() , or me, is used for ease of comparison with the corresponding vertical sonority in Example 3d.
, or me, is used for ease of comparison with the corresponding vertical sonority in Example 3d.
23 The common tone must connect a chord tone in the previous harmony to a chord tone in the following harmony; letter a in Example 3 is discounted by this rule because the G4 that follows the augmented-sixth chord in m.2 is a dissonance above the bass that resolves down to a chord tone.
24 Carissa Reddick has devised a detailed flowchart that helps students to consider the implications of the use of the augmented-sixth interval in various contexts and how they may be understood conceptually. Carissa Reddick, “Teaching Analysis of Chromatic Chords through Chord Qualities,” Music Theory Pedagogy Online, Vol. 2 (2013): 14 (see Example 11).
25 Harrison points out that this augmented-sixth chord is to be found in an inventory in the Harmonielehre (1920) by Rudolph Louis and Ludwig Thuille. Harrison, “Supplement,” 182. However, Harrison does not confer much importance on this sonority because these authors do not provide a practical application; Harrison offers an example in Verdi’s Requiem – cited by Ebenezer Prout – that Harrison deems is actually “a by-product of passing motion.” Ibid.
26 Harrison does not entertain ♭![]() & ♯
& ♯![]() in his list of privileged augmented-sixth dyads.
in his list of privileged augmented-sixth dyads.
27 When using the Socratic method in order to encourage students to determine their own conclusions, a combination of lower-order and higher-order questions is ideal. For example, in attempting to get the students to come up with a provisional interpretation of the sonority in letter d, one might begin with lower-order questions that elicit information the students already know: “List the three common elements that are found in all three types of augmented-sixth chords.” Depending on whether the students have been encouraged to think in terms of solfeggio syllables or scale degrees, the response will be either do, le and fi or ![]() , ♭
, ♭![]() & ♯
& ♯![]() . Because the students are asked to recall information that has already been disseminated to them, it is a lower-order question, which falls under the bottom-tier category of “knowledge” in Bloom’s Taxonomy. A follow-up question will ask the students to compare the augmented-sixth chord in letter c with the sonority in letter d and to identify the sole difference. Because identifying the difference between me, or ♭
. Because the students are asked to recall information that has already been disseminated to them, it is a lower-order question, which falls under the bottom-tier category of “knowledge” in Bloom’s Taxonomy. A follow-up question will ask the students to compare the augmented-sixth chord in letter c with the sonority in letter d and to identify the sole difference. Because identifying the difference between me, or ♭![]() , and mi or
, and mi or ![]() , is based on previous knowledge, it too is lower-order in nature, which falls under “comprehension” in Bloom’s Taxonomy. A higher-order question could then be asked: “Describe a possible syntactical role of the sonority in letter d.” Here, students are being asked to extrapolate a role based on their knowledge of other more easily identifiable augmented-sixth chords. Unlike the previous two questions – which are closed questions because a desired response is intended – when the students are asked to extrapolate – which falls under “synthesis” in Bloom’s Taxonomy – an open question is asked because, while the general character of the response is anticipated, an actual response is not.
, is based on previous knowledge, it too is lower-order in nature, which falls under “comprehension” in Bloom’s Taxonomy. A higher-order question could then be asked: “Describe a possible syntactical role of the sonority in letter d.” Here, students are being asked to extrapolate a role based on their knowledge of other more easily identifiable augmented-sixth chords. Unlike the previous two questions – which are closed questions because a desired response is intended – when the students are asked to extrapolate – which falls under “synthesis” in Bloom’s Taxonomy – an open question is asked because, while the general character of the response is anticipated, an actual response is not.
28 Harrison, “Supplement,” 184-85. Although it is problematic to give agency to an interval rather than to the innovation of the composer, the turn of phrase “different sonorous shadings” is spot on because it allows for spellings of the augmented-sixth chord that go beyond the trinity canonized in most traditional harmony textbooks.
29 The syntactical ambiguity found here, I believe, is an intentional feature created by the composer. There is another reason why the sonority in Example 4d is so challenging to interpret, which will be explained when the post-tonal elements present in the prelude are identified.
30 It is also intended to help fill a lacuna of Caplinesque analyses applied to Romantic literature. David Forrest and Matthew Santa provide a cornucopia of works that include the sentence in their study “A Taxonomy of Sentence Structures,” College Music Symposium Vol. 54 (August 2014), which is a boon for the instructor. However, of the actual analyses that are included in the article, very few are taken from the Romantic period; moreover, the analyses themselves – while doing a splendid job of delimiting the components of the sentence – do not include a harmonic analysis that helps to reveal the underlying syntax and its relationship to the phrases within the sentence.
31 Caplin’s discussion of the sentence is found in Chapter 3 of Classical Form. More examples from the First Viennese School can be found in William Caplin, Analyzing Classical Form: an Approach for the Classroom (New York: Oxford University Press, 2013), 33 ff. A concise description of the sentence is found in James Mathes’ The Analysis of Musical Form (Upper Saddle River, New Jersey: Pearson, 2007), 42-44. The Mathes resource is helpful because it includes examples outside of the First Viennese School (in this case, Chopin & Verdi).
32 Caplin identifies three (3) ways in which the basic idea may be repeated: exact, statement-response, and sequential. Caplin, Classical Form, 37-39. In reference to the Tchaikovsky example, it appears to be an exact repetition because both two-measure units begin with a clear declamation of the tonic harmony, the composer uses a voice-leading chord to prolong the tonic in each unit, and the melodic contour is retained – both units outline the span of a sixth from F♯5 to A4 in a descending gesture.
33 Ibid., 41-42.
34 The roman-numeral/figured-bass analysis has been parenthesized here because the sequential pattern is a device used to prolong the tonic. In addition, inversions of the harmonies in mm. 4 & 5 are not shown because they are obfuscated by the D pedal; besides, it has the benefit of evincing another example of the 9-8 suspension with which Tchaikovsky permeates this passage.
35 Invoking the concept of enjambment is immensely meaningful for freshmen students when differentiating the sentence from the period.
36 John Keats, Endymion, http://www.bartleby.com/126/32.html accessed on November 10, 2015.
37 Correspondingly, when looking the opening line of the Keats excerpt in isolation, “Nor do we merely feel these essences…” the reader is left contemplating a plethora of ways in which the “essences” are experienced, but the lack of punctuation compels the reader forward and a temporal element, “For one short hour,” contextualizes what was just read. As a result, the potency of the essences is underscored in that their cumulative effect will not be constrained by the passage of time.
38 When considering the second theme of the first movement, Caplin would argue that it demonstrates a tight-knit organization: “Tight-knit organization is characterized by harmonic-tonal stability, cadential confirmation, unity of melodic-motivic material, efficiency of functional expression, and symmetrical phrase groupings.” Caplin, Classical Form, 17. The last criterion, symmetrical phrase groupings, must be modified when addressing the literature of the Romantic period, which will be demonstrated in the Chopin example to be discussed next. Also, it strikes me that it is difficult to devise a workable yardstick for the “efficiency of functional expression.” An analysis can make a case for a plausible interpretation, but the “efficiency” (clarity?) resides in the ear of the listener.
39 Caplin also discusses the possibility of a pre-dominant harmony between the tonic and the dominant (specifically, he makes reference to Mozart’s String Quartet in C, K. 465, I, mm. 23-30. Caplin, Classical Form, 38-39). Moreover, there is another possibility when considering the first phrase of the Scriabin prelude because it could be an example of a hybrid theme, namely Hybrid #3 – compound basic idea + continuation. In this model, a compound basic idea is understood as “a phrase consisting of a basic idea and a contrasting idea that does not close with a cadence.” Caplin, Classical Form, 61. However, I do not hear the second two-measure unit as a contrasting idea but, rather, a repetition/response to the basic idea. First, in terms of rhythm, each unit begins with a long-short pattern (half/quarter), which is immediately restated in diminution (dotted-quarter/eighth); next, the contour of each unit is similar with an ascending gesture followed by a stepwise, descending line (sol to re in the statement and do to sol in the response). That being said, the descending line in the second unit is relegated to an inner voice as the right hand articulates a cover tone on A♭5. It is worthwhile to have this debate with the students because contemplating alternative interpretations – assessing the salient features in a different context – is conducive to promoting critical thinking skills. See Matthew Bribitzer-Stull, “Contention in the Classroom: Encouraging Debate and Alternate Readings in the Undergraduate Theory Class,” Journal of Music Theory Pedagogy, Vol. 17 (2003): 41-42 for suggestions on a “panel discussion” that will allow the instructor to structure this type of exchange productively.
40 Listening in “chunks” is imperative when discussing the concept of tonal ambiguity. After listening to this passage in its entirety, students will often not be fully aware of the conflicting tonal implications. Listening in “chunks,” parses out the competing tonal features and highlights the distinctions just discussed. Thus, when listening to the passage in a full texture once again, these subtle nuances will be better appreciated.
41 There is an elision between the basic idea and its counterpart because the double neighbour, B5 & G♯5, moves to A5 on the downbeat of m. 3, which is simultaneously the beginning of the repetition – this is depicted graphically, by the overlapping brackets. This passage holds another example of an exact repetition as well.
42 Caplin, Classical Form, 45-47. The arrow in this label is meant to convey becomes; thus, the continuation function becomes a cadential phrase, which Caplin says is “a retrospective reinterpretation of formal design.” Ibid. Mathes does not make this distinction in his discussion.
43 At the beginning of the B section, Chopin inverts the melodic contour found in the continuation phrase to become F♯5 to A4 in a descending gesture followed by a stepwise, ascending line to C♯5 (see mm. 21-22 of the prelude). Additionally, the harmonic progression used to support this inverted line at the beginning of the B section is identical to the progression in the continuation phrase shown in mm. 6-7 of Example 7. Thus, Chopin recycles this continuation material for the two-measure sequential pattern used in the B section.
44 The contrasting idea of the consequent phrase may or may not resemble the contrasting idea of the antecedent phrase. Ibid., 53.
45 It also shows an interesting innovation on the part of Chopin as the symmetrical 4 + 4 model is abandoned for an asymmetrical 4 + 3 model, which can foster a healthy and lively discussion in the classroom; indeed, by asking the students why Chopin would have made that decision, a rudimentary review of a formal paradigm becomes a dynamic discourse in compositional strategies.
46 Without a doubt, the Mozart excerpt in Example 2b foreshadows this compositional evolution.
47 The syllables printed immediately beneath the melody (an integer-based solfeggio system) are recommend by Joseph Straus in order “to maintain a single syllable for each note.” Joseph N. Straus, Introduction to Post-Tonal Theory, 3rd ed. (Upper Saddle River, New Jersey: Pearson Prentice Hall, 2005), 20 – I have been unable to locate these syllables in the 4th ed. In addition, both Straus and Roig-Francolí use the abbreviation ‘WT’ to designate a whole-tone collection; a subscripted ‘0’ indicates the collection with all even-numbered integers and a subscripted ‘1’ indicates the collection with all odd-numbered integers. Straus, Introduction to Post-Tonal Theory, 4th ed., (New York: W.W. Norton & Company, 2016), 252 and Miguel Roig-Francolí, Understanding Post-Tonal Music (New York: McGraw-Hill, 2007), 52. Before singing through Example 10, it is useful to get the sound of the whole-tone collection in the ears of the students. The Rogers/Ottman resource has excellent examples from the literature with which to practice. Nancy Rogers & Robert W. Ottman, Music for Sight Singing, 9th ed. (Upper Saddle River, New Jersey: Pearson, 2014), 387 ff. For an exercise that will help prepare students for the other examples in this discussion, which address tetrachordal subsets of the whole-tone collection, see Exercise 5.3 in Michael Friedmann, Ear Training for Twentieth-Century Music (New Haven, Connecticut: Yale University Press, 1990), 77 (it is recommend to work only with the tetrachords in Group 1 for beginning students).
48 The Adjacency Interval Series, AIS, morphs from <2,4,4> to <2,2,4>. Doing this exercise accomplishes two objectives: 1) it will help students to internalize the aural experience of this tetrachord and its constituent dyads, and 2) it will help to reinforce why the second tetrachord is the normal order as ic 2 is heard twice in succession. Furthermore, if students are taught to find the prime form via the AIS, this preliminary exercise will add an aural component to the abstract process of deriving [0248].
49 Regarding the benefit, or lack of benefit, of encouraging students to learn the Forte sc labels, the following observations are offered for consideration: 1) the distinction between a pc-set and a set class can be very challenging for novice students. The Forte sc labels help codify the distinction that a set class represents an entire family of pc-sets. In the case of the trichord, this notion can be explained in more familiar terms: Forte sc 3-11 includes all twelve major triads and all twelve minor triads; thus, if they learn that a c♯ minor triad (now understood as trichord {148}) and a G major triad (now understood as trichord {7e2}) both belong to sc 3-11, a familial relationship is underscored; the cardinal number at the beginning of the label indicates that a three-note set is identified, and the ordinal number that follows indicates that all of these trichords share the same dyadic DNA (in this case, one minor third, one major third, and one perfect firth) far removed from the chromatic trichords at the beginning of the list. However, if both of these trichords are rendered as prime form [037], students will be unclear, initially, that this is meant to be emblematic of an entire family of trichords because of its resemblance to a pc-set (prime form as set-class signifier is not intuitive). In addition, the actual pc-set is listed immediately after the Forte sc label, so that the pcs identified by students are recorded – providing validation for their hard work. Once the distinction between a pc-set and a set class is clear, the instructor is encouraged to use whichever convention is most beneficial. 2) There is a great deal of scholarly literature in which Forte sc labels are used, and the student will be at a disadvantage if this nomenclature is not reviewed. 3) In regards to Example 12, imagine that all instances of sc 4-24 were labelled as [0248] in the analysis; if part of the lesson plan it to prompt the students to recognize that each tetrachord is a literal subset of WT1, the even numbers of the prime form will cause confusion (for the sake of clarity, hairpin brackets { } are used for an individual pc-set, and the square brackets [ ] are used for the prime form of a set class).
50 Depending on the skill-level of the students, and the context in which this prelude is included in the lesson plan, the instructor is encouraged to be as specific or general as needed. For instance, if students have been made aware of the difference between literal and abstract subsets, this can become part of the conversation; conversely, if students have only just begun to delve into segmentation and deriving pc-sets then a more general direction is appropriate. To be sure, segmentation is a tricky concept for the students to grasp, and it can only be truly comprehended with practice. Hence, by giving the students a specific cardinality to look for, and by giving them a hint for the types of set classes to find in preliminary exercises, the students are less likely to flounder. In the present case, the students are aware that Scriabin has embedded a whole-tone scale in the melody and that the intriguing chord found in the anacrusis is in reality a tetrachordal subset of WT1. Empowered, the students can begin a productive and enthusiastic bout of sleuthing (if segmentation is introduced as a type of post-tonal detective work, rather than a pedantic process of cranking out pc-sets, enthusiasm is more likely to be the consequence). For the instructor, two valuable discussions on segmentation are found in Christopher Hasty, “Segmentation and Process in Post-Tonal Music,” Music Theory Spectrum, Vol. 3 (spring 1981): 54-73 and Stanley V. Kleppinger. “Strategies for Introducing Pitch-Class Set Theory in the Undergraduate Classroom,” Music Theory Pedagogy Online, Vol. 24 (2010): 131-156. For the student, see Straus, Introduction, 4th ed., 69-71 and Roig-Francolí, Understanding, 107-111. Straus provides a concise step-by-step process that is summed up with the dictum: “In all of your musical segmentations, strive for a balance between imaginative seeking and musical common sense.” Ibid, 70. Roig-Francolí provides a more nuanced discussion. For example: “When analyzing chordal structures (harmonies), at times we will consider only the actual chord. But at other times it will make sense to include, along with the chord, other pitch classes that may be presented simultaneously to the chord in one or more melodic lines. In other words, we can analyze melody and harmony separately, but we may also want to examine their interaction.” Ibid, 109.
51 The altered submediant chord holds two common tones with the E major triad: E and G♯.
52 Some of Scriabin’s later works fall into this category.
53 Robert Gauldin’s analysis of this song in his textbook makes reference only to “French 6th chord types.” Gauldin, Harmonic Practice, 762-64. While this sonority, that belongs to sc 4-25 [0268], is indeed an important part of the harmonic palette in this song, restricting the analysis to this tetrachord does not fully embrace the extent to which Berg is utilizing both whole-tone collections. Hence, all of the scs identified in Example 11b are subsets of the whole-tone collection, which can be corroborated by consulting Figure 1. Joseph Straus’ analysis is more comprehensive because, in addition to discussing important subsets of the whole-tone collection, important transpositional relationships are addressed, as are issues of text setting. Straus, Introduction, 143-48.
54 Regarding the distinction between “scale” and “collection,” the former is best used when one is dealing with the aggregate presented in a linear succession that has both a distinct starting point and ending point (see Example 10); the latter is best used when one is dealing with the aggregate as a collection of raw materials that can be used in sundry ways depending on the needs of the composer (see sc 6-35 in Example 12).
55In order to answer the “why is there only one pentachord?” question that will inevitably be asked, refer the students to the ic vector for set class 5-33 after first reviewing the ic vector for set class 6-35. Specifically, ask the students what is unique about the vector entries for both of these set classes. The students should recognize that the both vectors have no entries under the odd numbers (i.e., no semitones/major sevenths, no minor thirds/major sixths, and no perfect fourths/fifths). Now, some students may conflate the distinction between the integers used to differentiate the two types of whole-tone collections with interval classes; specifically, “if one is looking at a pentachord from sc 5-35 that is derived from WT1, shouldn’t there be entries under the odd numbers in the ic vector?” This is an ideal opportunity to engage in some review that will benefit the entire class. First, regarding the ic vector, the entries represent not pitch classes but interval classes; thus, the vector entries for all whole-tone chords, irrespective of cardinality, will only have even-numbered entries because the collection is built on successive major seconds (it is useful to remind students of the basic mathematical principle that the addition of two even numbers will always result in an even number). Regarding the two whole-tone collections – WT0 = {0,2,4 … t} & WT1 = {1,3,5 … e} – where each integer represents a distinct pc, impress on the students that, while one set is even numbered and the other is odd numbered, the distance between any pc is always a multiple of 2 in either set.
56 Richard Taruskin continues in this vein: “This is, one imagines, how Scriabin creates [his] “sound universes” – not by “selecting” pc-sets from the universe of all possibilities, but by exploring the specific possibilities afforded by the more immediate and restricted universes of their time and place, against a background of common practice that preconditioned their own hearing-and-understanding and made it sharp.” Richard Taruskin, “Review of The Music of Alexander Scriabin,” Music Theory Spectrum, Vol. 10 (spring 1988): 161. In addition, the preceding exercises and discussion also begin to address concerns about the analytical legitimacy of pitch-class set theory itself: “Pitch-class set theory also stands condemned for is failure to explain how music makes sense aurally … A theory that tells us how we hear music can, in principle, be tested … a theory that tells us how it has been conceived cannot.” Michiel Schuijer, Analyzing Atonal Music (Rochester, New York: The University of Rochester Press, 2008), 23. By asking students to discern/hear whole-tone elements in both the melodic dimension (the entirety of WT1) and the vertical dimension (tetrachordal and trichordal subsets), a clear listening strategy is encouraged – one that highlights salient features of the musical fabric.
57 The AIS can also be a very effective tool in assisting students to discern subset relationships. Given that Figure 1 lists the prime form of each set class, the student will be able to recognize literal subsets; for example, the pcs of trichord 3-8, [026], can readily be seen in the prime form of tetrachords 4-21 & 4-25 (i.e., [026] is a literal subset of these two tetrachords). However, the pcs of [026] are not present in the prime form of tetrachord 4-24 [0248]. Here, the AIS is an indispensable tool to evince the subset relationship. The AIS of [026] is <2,4>, and, although this series is not present in the first trichord {024} = <2,2>, it is present in the second trichord {248} = <2,4> (thought of another way, if one subtracts two semitones from trichord {248} one derives the prime form [026]). This same process can also be used to demonstrate why trichord [048] is not a subset of tetrachord [0268].
58 A discussion of the linear, chromatic harmonies in the inner voice (such as 3-1 {567} in m. 1) is not addressed here because the focus of the present discussion pertains to the whole-tone elements. However, at a subsequent discussion with the class, pointing out the creation of chromatic elements in the melodic dimension is most fruitful – see the Berg excerpt in Example 11b where sc 3-1 is also present.
59 Discoveries such as this underscores for the student the advantage of studying pc content via integers given the various enharmonic spellings used by the composer.
60 Arnold Schoenberg, “Composition with Twelve Tones (I),” in Style & Idea: the Selected Writings of Arnold Schoenberg, ed. Leonard Stein, trans. Leo Black (Los Angeles: University of California Press, 1975), 220.
61 Regarding the top system in Example 12, let A = {e137}, B = {57e1}, C = {9e15}, and D = {359e}: A ∪ B ∪ C ∪ D = 6-35 {13579e}.
62 James Baker, The Music of Alexander Scriabin (New Haven, Connecticut: Yale University Press, 1986), 41. Baker notes that Scriabin often exploits the complement relation when incorporating the whole-tone collection. Ibid., 10. Although WT0 is not used in a systematic way in this prelude, the composer does hint at it in the opening phrase via the sequential pattern: C as a key = 0, B♭ as a key = t, and A♭ as a key = 8.
63 Is this an example of how analysis can create a more astute listener or how analysis can create a confirmation bias?
64 Regarding the form of this prelude, Hull suggests that “all music should have the quality of ‘poetry in sound’ as one of its constituents. The Miniature forms serve either for tone-pictures, as with MacDowell; for little ‘Harmonic Studies’ as with Rébikoff; or for tiny Pastels of absolute music, as with Scriabine’s ‘Preludes.’” A. Eaglefield Hull, Modern Harmony: its Explanation and Application (Boston: Augener Ltd., 1915), 189. Writing eighty years later, Richard Taruskin continues the dialogue about Scriabin and absolute music: “In this he [Scriabin] remained true to the older, original concept of ‘absolute music,’ which, far from implying formalism, envisioned an instrumental music capable of directly incorporating and transmitting all the ineffable – which is to say, nonparaphrasable – expressive and metaphysical content at which the nature-imitating arts could only hint.” Richard Taruskin, “Scriabin and the Superhuman,” in Defining Russia Musically (Princeton, New Jersey: Princeton University Press, 1997), 321. The notion of Scriabin as composer of absolute music will be addressed shortly.
65 Roy James Guenther, “Varvara Dernova’s Garmoniia Skriabiana: a Translation and Critical Commentary (PhD diss., The Catholic University of America, 1979): 95.
66 Ibid., 101. Andrew Mead provides superb graphics that demonstrate the symmetrical properties of the whole-tone scale: a T2 cycle, the two embedded augmented triads (a Star of David), and the tritone exchange (a snowflake). Andrew Mead, “Shedding Scales, Understanding Intervals in Different Musical Contexts,” Theory and Practice, Vol. 22/23 (1997-98): 77. Mead also convincingly establishes that the whole-tone scale has just one scale-degree. Ibid., 78.
67 The keyboard texture of the original has been placed in a chorale-style setting to more easily observe the parsimonious voice leading: the arrows depict motion by semi-tone while the dashed line depicts a common tone.
68 In the list of set classes that Baker discusses in depth, found in the index, sc 4-21 is not present. Baker, The Music, 286.
69 Alfred J. Swan, Scriabin (New York: Da Capo Press, 1923), 91.
70 The Theosophy Trust has uploaded the teachings of Blavatsky to its website, which includes one on the significance of the number seven: http://www.theosophytrust.org/493-the-number-seven.
71 Alexander Scriabin quoted in Faubion Bowers The New Scriabin: Enigma and Answers (New York: St. Martin’s Press, 1973), 125.
72 Begin counting at m. 9, the beginning of the second sentence.
73 For a straightforward example of the 16-measure period to review with the class, see Mozart, Piano Sonata, K. 545, II, mm. 1-16.
74 See Caplin, Classical Form, 65.
75 Mathes, The Analysis of Musical Form, 99.
76 This last point might be considered by some as a distraction from the discussion thus far; however, I believe that the theory classroom must also interface with the historical milieu when it pertains to compositional choices. Such a contextualization reinforces for the student that what is discussed in the history classroom has a direct bearing on what is discussed in the theory classroom. The following cautionary note expands on this point: “The mistaken notion of theory as ‘objective’ or ‘data-driven’ can arise when theory instructors appear to be fixated on the score at the expense of the historical and cultural backdrop against which the music was written and received.” Mark Clague et al., “Building Bridges: Same and Different Issues Across Music Theory, Music History, and Music Education,” College Music Symposium, Vol. 49/50 (2009/2010): 143.
77 James Baker, “Scriabin’s Implicit Tonality,” Music Theory Spectrum, Vol. 2 (spring 1980): 2.
78 Caplin outlines these three categories but does not use the labels. Caplin, Classical Form, 23.