I. BACKGROUND
It is hard to imagine a more interesting moment to be a music theorist. This is the result of a unique obligation and opportunity: the urgent need for a wide-ranging reconception of music theory. It results from convergence of four recent forces:
historical—the reemergence, in the hundred-fifty years since the death of Beethoven, of Europe's distant musical past, reflecting other theories and ideals of sound than those of 18th- and 19th-century Europe;
cultural—the intermingling of musics of the entire world with their numerous coexisting classical traditions, and the evolution of new music cultures from their meeting—for example, the Afro-american;
scientific—the revelation by psychophysical analysis of many essential, hitherto unexpected elements of sound and its perception;
technological—the dramatic expansion of resources for synthesis, analysis, memory, and transmission of sound and music offered by electronic technology.
The result of these forces is to make available here and now, for virtually the first time, the sum total of all sonic and musical phenomena. Whereas previous limits were determined by instruments and memory, by cultures and history, the current limits are global and psychophysical. The boundaries stretch to the limits of sound and of the musical imagination. The unprecedented current task, then, is to provide means for illumination of the entire art of sound in ways responsive to the worldwide musical and scientific imaginations.
Since this was not the task of earlier theory it, not surprisingly, does not accomplish these aims. And since the enormity of the task defeats piecemeal solutions, even concerned, dedicated teachers working singly in isolation have foundered on waves of these dimensions. The new premises of theory require new concepts appropriate to them.
This article is written out of a decade of experience spent developing the outlines of a basic re-direction of theory and its teaching, embodied in the book Sonic Design: The Nature of Sound and Music.1 The entire approach developed there cannot be conveyed in this brief space. Consequently, I shall focus here only upon the aspect that is most novel, and that highlights the contrast between the assumptions of previous European theory and those of the new theory we propose. This is not done, let it be immediately noted, in a spirit of "either-or," but rather in a spirit of adding complementary possibilities—of developing alternative views of the nature of musical sound and order. It is the analysis of tone color, then, that has been chosen as the paradigm of the new approach.
II. RUDIMENTS OF TONE-COLOR ANALYSIS
For several thousand years the method of European theory has been reductionism. Phenomena of sound and music, often of staggering complexity, have been reduced to:
—single fundamental pitches;
—and, in fact, to very few of them—between seven and twelve to the octave;
—distributed in a few octave registers;2
—according to rhythms based on a few chosen ratios.
Here our procedure will be the opposite. We will attempt to investigate, measure, and define the ordering of the entire complex of phenomena identifiable as sonic or musical stimuli. While this sounds abstract, let me say at once that, on the contrary, it is immediate and concrete. It means dealing in the theoretical and teaching situation with such directly tangible factors as instrumental sound.
If we take two sonic events—for example C1 and C8 on the piano3—conventional theory assigns them to the same pitch class, C. Virtually all other perceptions depend upon that primary classification.
Let us, however, undertake their tone-color analysis. As is well known, tone-color analysis was initiated with Helmholtz's theory that tone color depends upon the number of partials in a sound and the relative intensity of those partials.4 Most sounds which seem simple and unified (or which previous theory led us to regard and hear in that way), such as "single musical notes," turn out upon analysis to be compounds or complexes of partials. The irreducible constructive element is the partial, or sine tone—the tone produced by a sinusoidal wave, a tone which does not produce any further partials of its own. Compound or complex tones are built up of different quantities and intensities of sine-tone partials, each compound or complex tone being a different "formula" or "recipe." In analysis such a recipe is called the spectrum of a compound or complex tone.
Helmholtz's theory, consequently, has a significance for sound similar to atomic theory for physical matter. It reveals a sub-structure of immense detail underlying, or (better) forming, the apparent surface. Like atomic theory it forces a re-examination of the nature of reality.
Ex. 1.
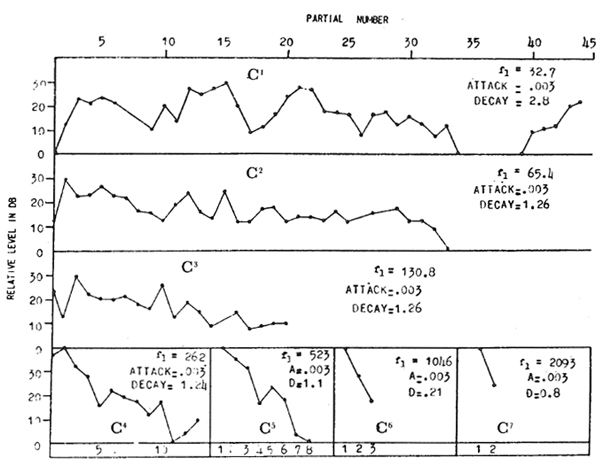
Spectra of C 's in 7 octaves of the piano (C 1-C 7). Each circular node is a partial.
After Fletcher (see ftn. 6). p. 753. By permission, Acoustical Society of America.
Ex. 1 shows spectrum analyses of C1-C7 on the, piano. The spectra of the lowest C's, C1-C3, have common characteristics:
—a very large number of partials (between twenty and forty-four);
—relative weakness of the fundamental, and greater intensity of certain upper partials.
Such a perception already conveys important information about C1 on the piano: that it is a compound signal comprising numerous strong separate pitches, many of them distinctly audible (and producing noticeable beats), which notational and theoretical conventions have reduced to a single fundamental pitch, C1. Thus, reductionism.
As we ascend the piano's registers in Ex. 1, the spectra change markedly. Beginning with middle-C (C4) the spectra are notably less rich. They reveal a falling off in quantity and intensity of higher partials, until with C8 only a single partial, the fundamental, remains. (This simple spectrum is, therefore, not shown.) In terms of spectrum as well as register, C1 and C8 of the piano stand almost at opposite poles.
Let us add here a further observation concerning the sine tone. Since it is a primary building block or constructive element, we must understand it well. When one hears a sine-tone sweep covering the entire audible range, one observes differences of sound quality in different registers. The color changes from duller oo(u)-like sound in the lowest registers to brighter ee(i)-like sound in the highest registers. This change is, of course, reflected in tone-compounds and complexes built out of sine tones: they take on added brightness as the quantity of high-register partials grows.5 Spectrum and register both, then, are crucial to tone color.
Moving on from Helmholtz's beginnings, later analysts of tone color realized that instrumental colors are more complicated than revealed by spectral analysis. For example, Harvey Fletcher in a classic study of piano tone color wrote:
It is true that the quality [or color] depends upon the wave-form [Helmholtz's differing partials with differing intensities]. But it also depends upon the pitch (especially register, as we have just observed), the loudness, the decay and attack time, the variation with time of the intensity of the partials, the impact noise of the hammer, the noise of the damping pedal, and also the characteristic ending of the tone by the damping felt, etc.6
Ex. 2 and 3 reveal aspects of these properties. Ex. 2 shows the change of spectrum and attack noise at three different dynamic levels for C2.
Ex. 2.
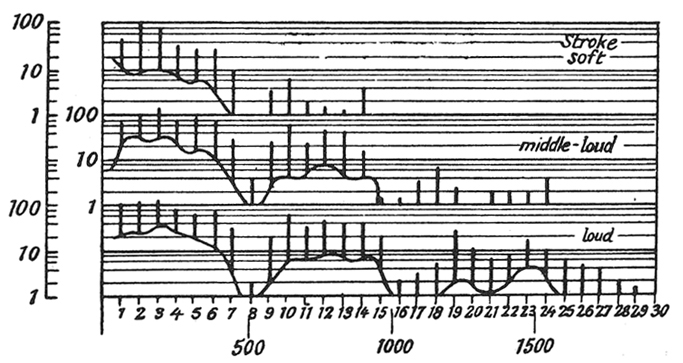
C 2, 65 cps, of the piano at three different dynamics. Vertical lines indicate relative intensity of partials. The curves indicate frequency regions and relative intensity of the impact noise.
After James Jeans, Science and Music, p. 96. By permission, Dover Publications, Inc.
Greater loudness generates partials and attack noise of higher frequencies. It should be noted, too, that attack noise assumes greater relative importance in higher registers, so much so that in the highest registers a wide frequency-band of attack noise is far more prominent than the few, relatively weak partials. Ex. 3 shows the "history" of the first six partials of C4 over two seconds of time. Certain partials disappear entirely; others decay; still others actually gain intensity—so that the spectrum, and consequently the color, is undergoing constant subtle change.
Ex. 3.
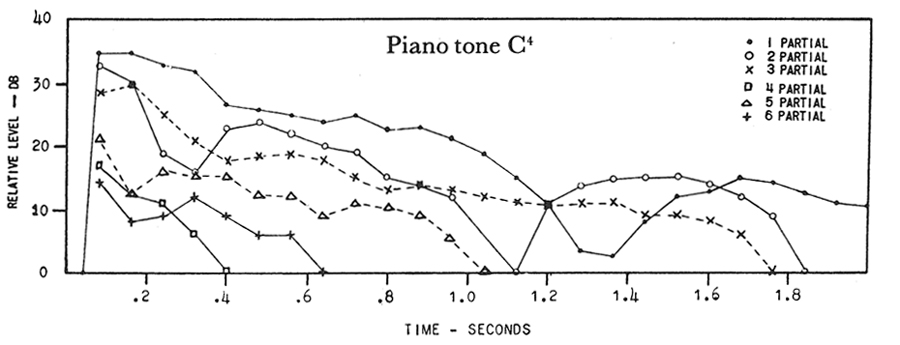
Variations with time of the intensity of partials 1-6 of C 4. After one second only partials 1-3 remain. The fundamental is considerably weakened.
After Fletcher (see ftn. 6), p. 754. By permission, Acoustical Society of America.
Fletcher learned that to synthesize tones acceptable as piano-like, one must deal with all of these factors. And also with an additional surprising one: that supposedly identical piano strings are not tuned exactly alike; that, due to the stiffness of those strings, many partials are also inharmonic (or "out of tune"); and that in addition to these intonation discrepancies, the extremities of pianos are tuned to a stretched tuning rather than to a just or tempered tuning. As a result of all these intonation variants, piano sound is constantly suffused by slow acoustical beats produced by near-adjacencies of pitch. A well-tuned piano includes a massive quantity of "out-of-tune," beating elements. These turn out to be necessary to piano sound. Synthesized sounds otherwise identical to piano sounds but lacking such discrepancies and beats are judged not to be piano-like!
So we glimpse the extraordinarily rich sonic actualities of piano sound, comprising:
—attack noise whose frequency, duration and relative intensity vary with register and loudness;
—the body of sound whose spectrum likewise changes with register and loudness, but also changes over time with variations of the partials' intensities;
—the whole suffused by beats, by the sound and resonance effects of pedaling, by the overall decay rate (also different depending upon initial loudness, register and pedaling);
—and ultimately, the conclusion of the tone by the damping felt.
A complex mass of sonic data. The one "fact" recognized by previous theory with respect to the C1 and C8 with which we began, their reduction to the pitch class C, is actually one of the more questionable possible generalizations. Rather than being entirely similar, they are characterized by radically different attacks, decay rates, and spectra. They are still further unlike, for they are especially affected by the stretched tuning just mentioned. Yet reductionist theory prefers to draw attention to its questionable pitch generalization rather than to the actual and massive sonic data!
There now exists raw material for something never achieved in two millennia of European theory: a genuine instrumental theory, deriving from and dealing with total musical sound. Such a theory, when developed, could engage instrumental musicians exactly where their deepest preoccupations lie. It offers the possibility of dealing with the whole sound of musical events, rather than with one, or very few, reductions abstracted from them. In learning, it turns out to be immensely revealing and exciting for students to perceive the actualities of their instrumental sounds in full analytic detail: the perceptible spectral elements; the duration, frequency and loudness of attack noise; transformations in spectra or attack due to dynamic or other changes; the elements which undergo change in tone-color modulations. Indeed, it is tempting to linger here, but to allow the reader to value such information fully, I must drive on to one further stage, a stage not achieved by our acoustical or psychophysical predecessors: the analysis of the unfolding of tone-color in an actual musical work.
III. ANALYSIS: SCHOENBERG'S "COLORS"
Originally named "Colors," later renamed "Summer Morning by a Lake," the central movement of Schoenberg's Five Orchestra Pieces, Op. 16 (1909), now appears to be rivaled only by several passages of Stravinsky's Le Sacre as the most stimulating and influential stretch of music composed in the early twentieth century. The embodiment of Schoenberg's idea of tone-color melody, for sixty years it has preserved its mystery, remaining analytically impenetrable even while affecting a host of diverse followers: Berg, Webern, Varèse, Carter, Ligeti, Stockhausen . . . to name the most obvious. In a revealing passage at the end of his Harmonielehre Schoenberg himself, the arch-analyst, confessed his inability to analyze such tone-color successions.7
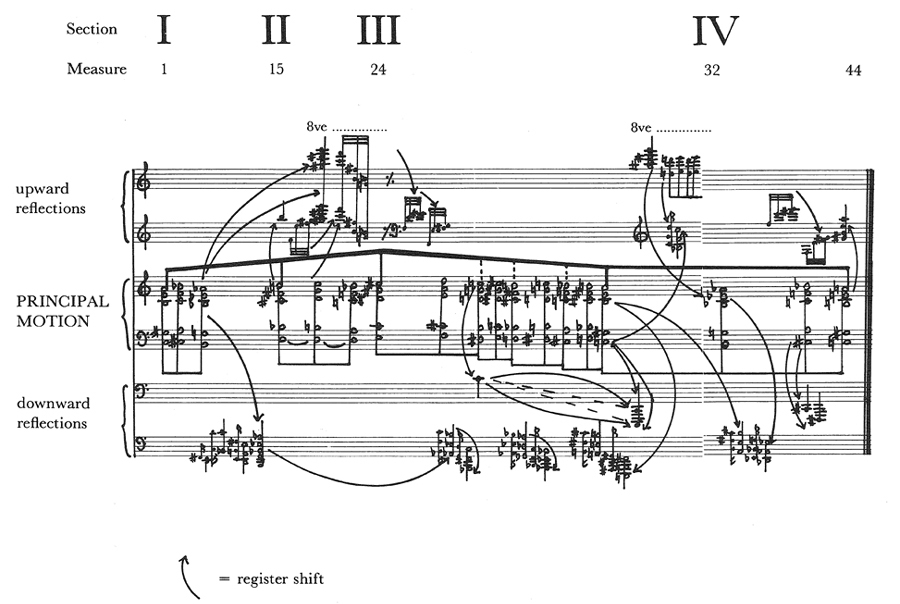
Ex. 4 lays out the movement's fundamental pitches.
Ex. 4.
By Permission, C.F. Peters Corporation.
from FIVE PIECES FOR ORCHESTRA, op. 16, Arnold Schoenberg (P #6061).
Copyright © 1952 by Henmar Press, Inc., 373 Park Avenue South, New York.
The principal motion of the piece is carried out on the example's central level, notated as half-notes:
—It consists of a single five-voice harmony moving throughout the entire piece in parallel motion according to a single cellular pattern of linear motion—a semitone rise, followed by a whole-tone descent.
—By sequences of this cell, the entire principal motion of this harmony executes a gradual ascent (in the soprano voice from its beginning on A4 to its apex, D5) followed by a rapid descent back to the A4 starting point—the total space covered by each voice is only a tritone; for example,
4-D5 in the soprano.
In the piece itself, as opposed to Ex. 4, staggering the motion of the voices creates an illusion of counterpoint, canon, and stretto; but ultimately the voices rejoin each other and parallel motion reigns. Let us note that at first glance the limitation of the motion's range to a tritone would seem an unpromising one for development of diverse instrumental colors.
In Ex. 4, one finds at intermittent points that elements derived from the principal motion are reflected outward into other registers, lower or higher. (This is often accomplished by direct register-shift of identical structures but sometimes by transposition of derived structures.) These momentary reflections intensify certain aspects of the principal motion. For example:
—The principal motion begins low (the lowest voicings of the harmony and of the cell—for example, A4-
4-
4 in the soprano) and then ascends; the relative lowness of the beginning is intensified by reflections downward throughout that part of the piece (Section I).
—On the other hand, the rise of the principal motion in Section II is intensified by upward reflections.
—Section III of the principal motion is characterized by the close climactic juxtaposition of the linear high and low points; in the reflections this is paralleled by juxtaposition of both upward and downward reflections.
By such means the minute directional gestures of the principal motion are written large and notably magnified by the reflecting register shifts.
The single harmony, its pattern of motion and the reflections (direct or derived) in downward or upward register-shifts account for all the fundamental pitches of the piece.
Keeping this layout of fundamental pitches in mind, let us now, proceed to its tone-color composition. The piece's principal motion (the movement already described, of the single five-voice harmony on the central level of Ex. 4) is presented not by a single fixed instrumentation, but rather by one that fluctuates throughout the entire piece.
Ex. 5 shows the instrumental fluctuation of the first section.
Ex. 5.

By permission, C.F. Peters Corporation.
From FIVE PIECES FOR ORCHESTRA, op. 16, by Arnold Schoenberg (P #6061).
Copyright © 1952 by Henmar Press, Inc., 373 Park Avenue South, New York.
The four winds of the first half-note (two flutes, clarinet, and bassoon) alternate regularly with those of the second half-note (two double reeds: English horn and bassoon; and two muted brasses: muted trumpet and muted French horn).8
Ex. 6 translates this alternation into spectral terms.
Ex. 6.

Thick lines represent fundamentals,
thin lines represent upper partials.
There in separate columns one finds an estimate of the spectrum of each instrument for its given pitch and dynamic. Following these are spectral estimates for the two sonorities, under the headings "first sonority" and "second sonority." (Ex. 7 shows samples of the tables, drawn from Seashore, Psychology of Music [New York, 1938] which are sources of instrumental spectral information.)
Ex. 7.

We can now compare spectral estimates9 of these two sonorities. In the first sonority the great bulk of energy is concentrated in Register 4, the register of middle-C; concentrated especially in fundamentals falling in that register, with only minute traces of higher partials. By contrast, in the second sonority there is a strong upward shift of energy to higher partials. The most intense partials are located in Registers 5 and 6, while traces stretch through Reg. 7. The same fundamentals in the two sonorities activate notably different configurations of partials.
The reader can test for him/herself the degree to which spectrum analysis represents sonic reality by listening carefully to these sonorities.10 Especially if they are taped and played at half-speed do spectral elements become clearly perceptible. In such a case, of course, everything sounds an octave lower than notated; however, an upward shift of an octave between the spectral concentration of the first and second sonorities is astonishingly vivid—so that the second sonority seems to be an octave higher register shift of the first!11
On such a slowed-down hearing there is time to notice other color elements as well. Within each sonority are pulsations or fluctuations. They result either from acoustical beats, or from the amplitude or frequency modulations that have come to be grouped under the general term vibrato. In Ex. 8 the beats produced by each sonority are measured.
Ex. 8.
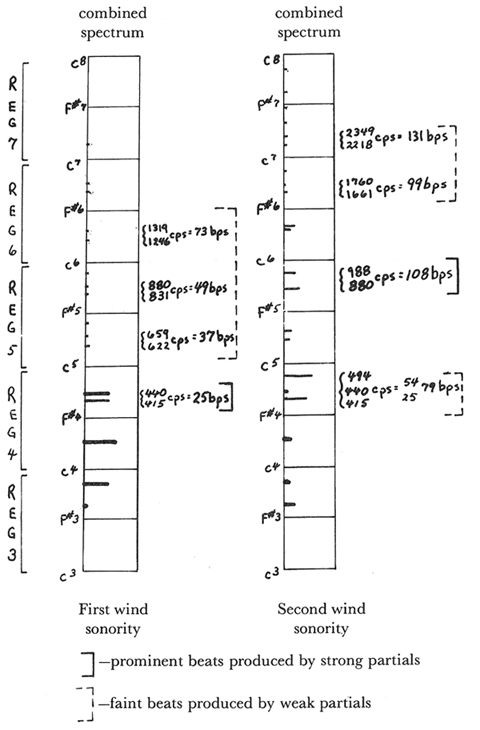
The most prominent beats are heard in the first sonority, created by the adjacency  4-A4: 440-415 cps = 25 bps. In this same sonority the two flutes produce amplitude modulations especially prominent in low flute sound, at a speed of ca. 6 modulations/second.12 In the second sonority the beat fluctuations are faster and more diffuse, the most prominent being 108 bps. Here, too, the two sonorities contrast: the pronounced relatively slow throb of beats and amplitude modulations (ranging between 6 and 25/second) of the first sonority dissipating in the second.
4-A4: 440-415 cps = 25 bps. In this same sonority the two flutes produce amplitude modulations especially prominent in low flute sound, at a speed of ca. 6 modulations/second.12 In the second sonority the beat fluctuations are faster and more diffuse, the most prominent being 108 bps. Here, too, the two sonorities contrast: the pronounced relatively slow throb of beats and amplitude modulations (ranging between 6 and 25/second) of the first sonority dissipating in the second.
I do not mean to wear the reader down with measurement of every sonic element of these two sonorities. Those mentioned, however, are perfectly audible, and form the basis for the continuing color transformations of the piece. For example, the presence and variation of beats and amplitude fluctuations create that "shimmer" of sound analogous to light on water alluded to in the piece's second title, "Summer Morning by a Lake." Before completing the analysis by tracing the systematic transformation of spectra and other elements of color through the piece, let me emphasize that even here—with two sonorities whose identical fundamental pitches sound at a single dynamic—we have been able to define precise characteristics of color and its transformation, and even to find implications of registral motion and changing rates of activity. These foreshadowings will be confirmed in the upcoming transformations.
Now to extend the analysis to encompass the entire piece. Rather than analyze every spectrum in detail, each will be analyzed according to a spectral scale. Ex. 9 demonstrates the basis for such scaling.13
Ex. 9.

For a number of instruments it gives the spectra of a single note and dynamic, G4 (392 cps) at piano dynamic. Reading across the example from left to right, the spectral energy ascends; the colors shift from duller to brighter. Extending the same process, Ex. 10 then ranks all of the instruments used in the presentation of Schoenberg's principal motion on a numerical scale from one to eleven.
Ex. 10.

"One" represents the lowest spectral concentration of energy: virtual sine-tone character, lacking strong higher partials. "Eleven" represents the highest, brightest sounds resembling, in audio terms, those where a high-pass filter eliminates the fundamental and low partials, allowing only the highest to pass.
Ex. 11 is an analysis, according to this scaling, of every sonority participating in the principal motion of the piece:
Ex. 11.
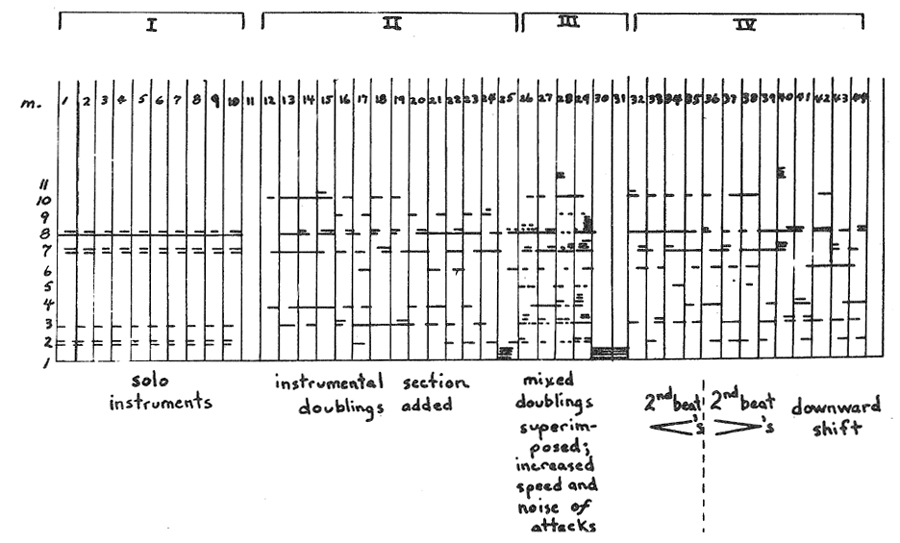
Section I. Rewritten according to the spectral scale is the fluctuation between a duller and a brighter sonority previously demonstrated in the composite spectra (Ex. 6). We can now notice how very dull, by comparison with later sonorities, the initial sonority is, consisting primarily of the lower groups, 2 and 3, on the scale. The contrasting second sonority draws on groups 7 and 8 (muted brass and double reeds).
Section II. The addition of groups 9 and 10 (unmuted strings, in sections and solo) to the previously used groups 7 and 8 significantly brightens the entire section's tone color. The reader will recall that in this section the added intermittent reflections by register shift also turn upward, as does the linear direction of the principal motion. There is a direct correlation between the upward register reflections and the upward shift of new higher-spectrum colors. Indeed, there exists between principal motion, reflections and spectra a threefold coordination, brightening the tone color.
At the same time it should be noticed that the newly added string sections also increase the quanta of beats (by choral effect) and vibrato.
Section III. In this section's principal motion the fundamentals attain (and fill in spaces between) the extremities. Furthermore, upward and downward reflections are brought together to greatly magnify by contrasting registers that juxtaposition of extremities. So too, this section's spectra form the piece's most complex, intense mixtures. High, bright and low, dull colors are combined in them. Finally, too, in mm. 28-31, the very extremities of spectral characteristics are juxtaposed. For example, group 11 (the highest spectra) in m. 28 is opposed to the group 1 concentration (the lowest spectra) in mm. 30-31. Here again the three levels—principal motion, reflections, and spectra—are coordinated, this time to maximize contrast and complexity, achieving thereby the piece's greatest intensification of tone color.
In other respects, too, this section's colors are the most complex. They fluctuate rapidly rather than slowly, and for the first time include significant attack noise. Furthermore, they are filled with vibrato (for example, from strings), with beats (generated, among other things, by the greatest amount of doubling), and even with tremolo. Indeed, these elements at their peak, m. 29, lend to the color the complexity of white noise. The direct contrast of this white-noise-like sonority with the following sine-tone-like sonority (mm. 30-31, consisting solely of group 1 color; and lacking significant attack-noise, beats, vibrato or tremolo), this juxtaposition climaxes the piece. It sums up the entire available range of tone-color contrast: on the one hand white noise, on the other the sine tone.
Section IV. The primary tone-color evolution of the piece occurs through Sections I-III, as described above. Following that, to conclude the piece Section IV works back to the initial tone-color state. The complexity and intensity of colors is gradually scaled down, so that by the concluding measures (mm. 43-44) the highest spectra (groups 11, 10 and 9) as well as the lowest (group 1) have all been eliminated. This return to the original state yet again parallels the principal motion, which by retrograde turns back through the initial cell of motion.
So we find that we can analyze, for the first time, the tone-color unfolding of a whole piece. In doing so we discover that the implication of movement embodied in the color elements of the initial sonorities:
the rise and fall of their spectral concentrations; the quickening and slowing of their inner activity, as in beats;
foreshadows the entire tone-color evolution of the piece—the brightening rise of the spectral concentrations, and the quickening activity of the most minute tone-color elements, throughout Sections II and III, before their falling off again in Section IV. And maintained throughout this entire pattern of transformation is the alternating pulsation of color-contrasting local events. We have already noted how remarkable the initial gestation of motion and activity in measure one is, since it is conveyed purely by tone-color elements without movement of fundamental pitches, dynamic change, or overt rhythmic difference.
In the piece the tone-color evolution reveals the most constant compositional attention and imagination; it bears the greatest structural weight. The actual movement of fundamental pitches in the principal motion (when it happens) is an additional seed, a microcosm. The upward and downward reflections form significant reinforcements, hints and glimmers. But the tone-color evolution—the succession of changing spectra, beats, tone modulations, and attacks—is the blossoming, the macrocosm, the great sonic and structural reality itself. It is a structure only perceived by recognizing the entire host of sonic elements left unrecognized by earlier reductionist theory.
IV. CONCLUSION
Another tradition of "water music," "Water Images" from the Japanese Kabuki theatre,14 reveals a similar sonic vision. Similar, but not identical. It begins with ten separated, slowly repeated D4's; each attack and decay, spectrum and resonance, loudness and duration is different—a music not conceived as movement of fundamental pitches, but including the subtle suggestions of movement and change we have found even with identical fundamental pitches. The analytical procedures developed above, and at length in Sonic Design that illuminate the one music also serve to illuminate the other. Music cultures which systematically cultivate spectral differentiation, attack differentiation, or continuous tone modulation (as in Chinese ch'in music), or those which cultivate the generation of beats of different speeds and intensities (as in Indonesian gamelan music) require theory with a place for those sonic properties.15
Indeed, whether it is European orchestra music of Berlioz, Mahler, Debussy, and Stravinsky; or the great bulk of recent instrumental composition conceived as "color design" (to use the painter Albers's term);16 or electronic music, whose every sound is a specifically synthesized color; or many of the classical musics of Asia; or the jazz improvisation of a Red Allen—tone-color understanding is a primary requirement.
We have previously tried to understand music by a theory largely instrument and tone-color blind. It has been inherited from European traditions harking back to anti-instrumental medieval religious biases; and, even further, to ancient Pythagorean number mysticism that recognized only a very few numerical relationships—as in the conventions of European rhythmic and intervallic theory. This led to the substitution of theoretical, notational reductions for sonic reality. Undoubtedly there exist instances where such reduction corresponds to a music's essential impulse, and little is lost thereby. But it is folly to reduce all music so.
It is our particular good fortune to have available on every hand through musical creation of the past hundred-fifty years, and through the rediscovery of marvelous and ancient cultures, music which shapes the entire sonic reality. And to have equally at hand theoretical means for perceiving and apprehending it. The theory that accomplishes this will bring about many reformulations of our musical and theoretical habits:
—It will no longer be necessary to reduce every sonic event to a single fundamental, or aggregation of fundamentals.
—Motion will not be understood in terms of notation alone; and a new significance for wide-ranging registral motion will emerge.
—Such elements as acoustical beats and so-called noise will be viewed not as irrelevant or undesirable, but rather as positive and necessary (in the right places!), susceptible to shaping and analysis in their own right.
—And finally, color will no longer be regarded as "surface"—surface being more characteristic of previous ways of regarding it, than of the parameter itself.
For we can now substantiate Schoenberg's intuition when he wrote of tone-color melodies and successions: "What fine senses discriminate here, what highly developed spirit which can find satisfaction in such subtleties!"17
Such a theory will prove advantageous at two levels. At the practical level there will be the advantage to instrumentalists of learning the sonic resources embedded in their instrumental sounds. Thereby will come direct relevance to performance. At the same time it will offer new opportunities for understanding a variety of musics, from Asiatic and Afro-american on the one hand to contemporary instrumental and electronic on the other, which for too long have eluded satisfactory analytical explanation because their essential tone-color content has been ignored.
1Co-author, Pozzi Escot, forthcoming in 1976. The present article is issued by permission of Prentice-Hall, Inc., publishers of Sonic Design. See also Robert Cogan, "Teaching Music Theory," Journal of Music Theory, Spring 1974.
2The Medieval European modal limitation to a single octave register should be recalled in this connection. See Willi Apel, Gregorian Chant (Bloomington, 1958), pp. 133-35. By comparison, from early antiquity vocal theory in the Indian raga system recognized three octave registers. See Alain Danielou, Northern Indian Music (London, 1949), p. 24. European composition has only very slowly outgrown its severe registral limitations; its theory, even more slowly.
3Registers are numbered according to standardized international acoustical terminology. The lowest C on the piano is C1; its register is Reg. 1. The next-lowest is C2; then the next-lowest is C3. Middle-C is C4, etc. Each successive C begins a new register.
4Hermann Helmholtz, On the Sensations of Tone (2nd Eng. ed., tr. A. Ellis, 1895, rpt. 1954), p. 56.
5R. Plomp, Experiments on Tone Perception, pp. 131-33.
6Harvey Fletcher, E. Donnell Blackham, Richard Stratton, "Quality of Piano Tones," Journal of the Acoustical Society of America, 34 (1962), 749.
7Arnold Schoenberg, Harmonielehre (Vienna, 3rd ed., 1922), pp. 506-7.
8The tone-color analysis always deals with colors of the upper four voices of the five-voice harmony. The lowest voice maintains a separate identity (different, more constant instrumental coloration; its own rhythmic period of oscillation; etc.). Consequently, it does not participate in the transformations effected by the upper voices.
9It must be emphasized that the spectral presentations are rough estimates. The information in the instrumental tables is limited by the pitches and dynamics analyzed for each instrument. In preparing the graphs it has been necessary to choose the closest pitch and dynamic for which spectral information is available. Other technical factors (dynamic differences between instruments; masking) have not been accounted for. However, due to the specified soft, equal dynamic level, their effect on these examples would be slight.
10The most accurate, revealing recorded performance now available is Nonesuch 71192: Gunter Wand conducting the Gürzenich Orchestra of Cologne.
11In this way the spectral register shifts prepare for the forthcoming register shifts in the reflections.
12Strong and Clark, "Synthesis of Wind-Instrument Tones," Journal of the Acoustical Society of America, 41 (1967), 48.
13I am greatly indebted to Mr. John R. Francis for Exx. 8-10, which work out the details of a spectral scale and its application to this piece. Such simple scaling is only feasible where change of register and dynamics is minimal, as in the principal motion of "Colors." Otherwise an instrument might find itself in several scalar positions depending upon spectral changes caused by different registers and dynamics. Even the scale offered here, however, must be understood as an approximate model approaching reality, rather than as absolute reality itself.
14Columbia record ML 4925, the Azuma Kabuki musicians.
15See Cogan and Escot, Sonic Design, Part IV.
16Josef Albers, Interaction of Color (New Haven, 1963), p. 42.
17Harmonielehre, pp. 506-7.


