I
In his article, "Music Theory: A single or multiple view?",1 Roland Jackson makes a persuasive case for a diversified rather than a unified approach to analysis. His argument is especially pertinent to music of transitional periods, which, by its very nature, exhibits structural tendencies toward the new while retaining a grasp on the old. Too often a square peg is jammed into a round hole, producing an analysis which, while justifying itself, misses the mark. Until a meaningful unified theory is invented, it would appear that a multiplicity of approaches is necessary. Scalar Control is one such theory which I believe sheds new light on some old problems. It is not advertised as a panacea for all analytic ills, but it is an approach of which we must be aware if we are better to understand certain music of the early 20th century.
By scalar control is meant that: 1) the harmonic flavor of the sum total pitch content of a given scale (mode) replaces the harmonic control exercised by an hierarchy of functional chords revolving about a central tonic; 2) as in the modal system, a given referential group may be systematically inverted. In effect, every scale has its Dorian, Phrygian, etc., positions. On the surface this would appear to be an euphemistic description of serialism. Not so. Scalar implies not the chromatic totality—which is no scale at all—but a set of pitches less in number than the twelve available. There is a peripheral but nonetheless important connection with serial technique in that several such scales, mainly hexachordal, do lead naturally to the number twelve, which makes this study all the more pertinent as it fills in some of that dead theoretical space which now exists between late nineteenth century chromaticism and serialism.
For the sake of argument, let's assume a position diametrically opposed to that of history's: that scales are the function of chords, that a given chord generates a set of scales which in turn constitutes the chord's color spectrum.
CATEGORY A
| 7TH CHORD TYPE | SCALES | SCALES (in inversion) |
| 1. Major | Ionian | Harm. mi. (6)* |
| Lydian | Gypsy (5 & 6) | |
| 2. Minor | Dorian | |
| Aeolian | ||
| Phrygian | ||
| 3. Dominant | Mixolydian | Mel. mi. (4 & 5) |
| Harm. mi. (5) | ||
| 4. Half-Dim. | Locrian | Harm. mi. (2) |
| Mel. mi. (6 & 7) | ||
| 5. Aug./Major | (none) | Harm. mi. (3) |
| Mel. mi. (3) | ||
| Gypsy (3) | ||
| 6. Minor/Major | Mel. mi. | |
| Harm. mi. | ||
| Gypsy |
| * refers to inversion at the 6th degree |
To illustrate: there are seven different tertial seventh-chords inside of the chromatic octave, assuming all possible superimpositions of major and minor thirds; six of these I shall place in category A (those having an outer limit of a major or minor seventh). Add to this the further observation that the chromatic distance between, but not including, the notes of a major third is three semitones; between the notes of a minor third: two semitones. Simple arithmetic indicates that a given tertial seventh chord will yield a predictable number of scales according to its distribution of major and minor thirds. In all, the six chords in category A generate a total of 90 seven-note sets. They fall into three classes: 1) those containing only whole and half steps, 2) those with one augmented 2nd, and 3) those with a pair of augmented 2nds.
The first class totals 18 possibilities, but this number is reduced to a mere three after inversional duplications take their toll: 1) the white-note set (all seven modes are represented), 2) the melodic minor (also present in all inversions), and 3) four different positions of a scale which places the two half-steps consecutively or at either end. Persichetti lists two of these configurations as the "Leading Whole-Tone" (ascending) and the "Neapolitan Major" (descending).2
The 48 sets in the second class are reduced to 16 by inversional duplication. Only two are present in all possible positions: the harmonic minor and what could be termed the "harmonic major," i.e., a major scale with a lowered sixth degree. Although the latter might conceivably appear in one or another lexicon, it has little or no visibility in the literature and, like the referential set in class one which includes the Neapolitan Major, must be discounted in this study.
The third class of 24 boils down to eleven by duplication. The presence of two augmented 2nds is a debilitating factor, forcing an intervallic content in any given scale of one whole and four half-steps. Only one configuration overcomes this handicap: The Gypsy, which appears in four of its positions.
The inversions of the various modal sets are not listed as they are all included in one referential group. Therefore, it is to be assumed that the minor seventh chord would spawn the Ionian mode on its 2nd degree, etc., etc. Were we but dealing with the modes this particular exercise would seem trivial, as their inversional relationships are well-known to history. Not so with the other scales. The acceptance of the principle of invertibility is important to the formulation of scalar theory. Let's turn now to an examination of the 7-noters produced by the foregoing analysis. First, the modes.
By admitting the intervals of the 9th, 11th, and 13th into the harmonic fold, the late 19th century recognized that a fully-voiced 13th chord is no more than a tertial resetting of a 7-note scale. The white system contains seven such sets, the most valuable in a control sense, i.e., regarding functional consonance as preferable to dissonance, being the Lydian and the Dorian, which work together as a major/minor team much like their Ionian and Aeolian brothers.
Ex. 1
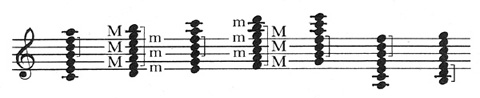
Unlike any of the others, the Lydian and the Dorian each contains an augmented-4th (11th) rather than a diminished-5th tritone as well as a balanced set of alternating major and minor thirds. This latter symmetry is of particular import with regard to the principle of pan-modality, which is based on the avoidance of the tritone in much the same manner as the musica ficta of the Middle Ages. Consider the following construction:
Ex. 2

2a is all white, and although the outer lines are melodically Dorian, the diminished-5th tritone, especially when its guide tone (G) is present, tends to keep the progression pointed toward its referential center of C major. 2b avoids the diminished 5th by raising or lowering as necessary the F or C, thus making each vertically Lydian or Dorian according to its particular tertial arrangement. 2c avoids the tritone by lowering or raising the B or E. In each of the latter two constructions the sense of dissonant tonality is lessened and that of consonant modality increased.
In addition to the modal scales, category 2a contains two other time-proven sets: the melodic and harmonic minors. Interesting structures appear as they undergo inversional tertial examination. First, the melodic:
Ex. 3

My use of G as root-tone in the foregoing example is for good reason. A practiced eye will immediately recognize the connection between this set and the first seven notes of the row Berg uses in his violin concerto.
Ex. 4

Theorists invariably point out the triadic superimpositions and the inclusion of the open strings of the violin in this set. Berg likely saw something else: the melodic minor scale inverted at its 4th degree contains all pitch-classes in the first thirteen partials of the (new) root-tone (ex. 3b). For this reason this particular inversion is better referred to as the Overtone scale (ex. 3c), a far truer "chord of nature" than Scriabin's much-ballyhooed invention, and more valuable; so much so that it must be regarded for control purposes as the prime position of its referential group (ex. 3a, lower line of numbers). The scale's connection with the harmonic series makes it particularly static (ergo, valuable) in a control situation; no inversion is impossible. As an example, I refer you to bars 38-39 of Ravel's "Ondine" (from Gaspard de La Nuit), which fairly crawls with the sound.
A tonal analysis would likely view bar 38 as a  dominant complex, with the E-natural consigned to non-harmonic status (i.e., an "appoggiatura chord"). A scalar approach produces an
dominant complex, with the E-natural consigned to non-harmonic status (i.e., an "appoggiatura chord"). A scalar approach produces an  Overtone (2) with all tones consonant; bar 39 places the scale in its root position. A fascinating "polychordal" aspect of the scale is thus revealed: two dominant sevenths, the lower one functional (if function is desired), the upper coloristic, an attribute which Stravinsky was to exploit several years hence in the Rite of Spring. Ravel does use so-called appoggiatura chords, but the assigning of all unexplainable non-harmonic activity to this grab bag is too simplistic an approach.
Overtone (2) with all tones consonant; bar 39 places the scale in its root position. A fascinating "polychordal" aspect of the scale is thus revealed: two dominant sevenths, the lower one functional (if function is desired), the upper coloristic, an attribute which Stravinsky was to exploit several years hence in the Rite of Spring. Ravel does use so-called appoggiatura chords, but the assigning of all unexplainable non-harmonic activity to this grab bag is too simplistic an approach.
The harmonic minor presents a problem, the augmented 2nd. Let's look at how it inverts.
Ex. 5

I have not used the A-flat scale out of sheer perversity. A close look at the 6th degree (on F-flat) reveals a configuration which any third-year theory student should be able to recognize as the basis for the infamous chord heralding the "Augurs of Spring" in Stravinsky's early masterpiece. Theorists generally tend to regard this structure as a polychord (an E-flat 7th over an F-flat major triad), which is as questionable a concept as is polytonality. In this regard I cite Arthur Berger's view (with reference to the "Petrouchka chord"): ". . . since the entire configuration may now be subsumed under a single collection with a single referential order . . . , the dubious concept of polytonality need no longer be invoked."3 The polychordal interpretation is suspect on another level. The three upper notes are obviously the ostinato figure (Ex. 5b). The G, despite its being grouped chordally with the pitches of the ostinato in the score, is better viewed as a modifier of the F-flat triad, producing an augmented-11th sound so typical of Stravinsky's later works. The inversional principle is seen here to its best advantage: the scale in this position has a strong combined major/minor feeling. Despite this unexpected jewel, however, the harmonic minor has not been a particularly valuable control. To my knowledge Stravinsky used it only during the Rite and even then in a limited way.
The last of the 7-note scales to be considered is that oddball, the Gypsy, well-named, as it has never found a real home in the harmonically-oriented West. It is profaned continually by film composers, who usually send it chasing off down a dark alley in Istanbul after some James Bond antagonist. Despite its forbidding appearance, it holds an exciting set of harmonies, including a pair of French sixth chords, a major 7th on the dominant, and a lovely Machaut cadence between the seventh and first degrees. An intervallic analysis reveals a brace of exotic tetrachords which produce a mirror inversion from the point of conjunction at the fifth tone, leaving a full-step at either end depending on the desired final (Ex. 6a).
Ex. 6

Bela Bartok utilizes this symmetry beautifully in the final bars of the first movement of Music for Strings, Percussion and Celeste (Ex. 6b). The cadence could easily have been written as in Ex. 6c, continuing the inversion until the double octave was reached. But the AE-flat dichotomy controlling the movement was of pivotal importance, so he chose instead to split the "left-over" full-step into two halves, moving both voices to the E-flat octave. The trip back employs an inversion of another class-3 scale (Ex. 6d) extracted from the augmented/major seventh chord, and composed of disjunct, mirrored tetrachords which place the augmented 2nds at either end. The full-step, on either flank in the Gypsy, is thus positioned right in the middle of a balanced formation, enabling both voices to split the difference and collapse to the unison.
THE NUMBER 5
The pentatonic scale, having no tritone, evades any particular tonal or modal responsibility. Its main significance other than its folk-melodic use comes not from its peculiarly static state, but because gaps are provided, the filling of which results in all of the church modes but one, the fictitious Locrian; and the Overtone is thrown in as a bonus. For this reason it should properly be appended to category A. Debussy was a past master in using the Pentatonic as a gapped structure, two excellent passages for study being found in La Mer, 1st movement, bars 31-42 and 72-75. In each instance an Overtone is combined with a Pentatonic ostinato. The latter example is particularly interesting as it exhibits a multi-layered texture much like that employed a short time later by Stravinsky in the Rite of Spring.
But perhaps the finest example of the Pentatonic's chameleonic personality is "Music to Scene One," The Soldier's Tale. The scale itself does not figure in Stravinsky's melodic/harmonic equation, but acts rather as an immutable core throughout, bolstered by the bass ostinato: G.D.A.G. (Ex. 7).
Ex. 7

The pitch-aggregate, the "superscale," is a nine-note complex from which every pitch in the piece is drawn, resulting in an effect best described as "parallel modality."4 Stravinsky is free to move at will from mode to mode, as in the opening section, which progresses from Mixolydian to Ionian to Lydian (all rooted on G) by the simple expediency of adding first an  (bar 17) and then a
(bar 17) and then a  (bar 27). As the piece becomes more complex texturally, modes are superimposed, producing at times the major/minor mix so characteristic of the composer's music. Bars 53-60 find the violin and bass arguing inside of a G Overtone, only to be interrupted at bar 61 by a quasidiodic passage (clarinet/cornet vs. bassoon) employing all of the possible scalar options simultaneously: in other words, the "super-scale."
(bar 27). As the piece becomes more complex texturally, modes are superimposed, producing at times the major/minor mix so characteristic of the composer's music. Bars 53-60 find the violin and bass arguing inside of a G Overtone, only to be interrupted at bar 61 by a quasidiodic passage (clarinet/cornet vs. bassoon) employing all of the possible scalar options simultaneously: in other words, the "super-scale."
Ex. 8

CATEGORY B:
Scales derived from the augmented triad and the diminished seventh chord.
A superimposition of augmented triads produces two relatively static scales, the better-known being the Whole-Tone, popularized by Debussy, who saw in its symmetry an easy—perhaps too easy—escape from tonality. Like the Pentatonic, the Whole-Tone emasculates the tritone, not by exorcism, however, but by proliferation; its singular importance is thus weakened. Its employment is so well chronicled that it would serve no useful purpose at this juncture to add to the already voluminous number of examples of its use. A much more fascinating but hardly as exploited 6-note set is built by superimposing two augmented triads a semitone apart. I shall refer to it as the 6-Tone Chromatic. At first glance it would appear rather awkward with its three augmented 2nd (minor 3rd) gaps. But an exciting theory develops as hexachordal combinations are examined.
Ex. 9

Observations
1) The scale is symmetrical, turning on three axes positioned a major-third apart; the axes are the upper notes of the minor seconds.
2) Any given set contains three major and three minor triads (plus major sevenths) based a major third apart; and two augmented triads (all tones potential roots).
3) Sets 9a & 9b and 9c & 9d are "disjunct," i.e., they share no notes in common. Their simultaneous or consecutive use would lead to at least a quasi-serial structure.
4) Sets 9a & 9c, 9b & 9c, 9a & 9d, and 9b & 9d are "conjunct," i.e., they share a common augmented triad. Their simultaneous use provides a nine-note control;5 their consecutive use a smooth, kaleidoscopic change in root orientation akin to tonal modulation.
5) Most important: the scale has no tritone.
Obviously, we are encroaching on 12-note theory with this symmetrical set,6 Webern's Opus 24 being a prime example of its use. But the set is not necessarily atonal. Consider this well-known fragment from Ravel's 2nd waltz from Valses nobles et sentimentales.
Ex. 10

This can hardly be called a control at this stage, but there's no denying that Ravel, much of whose music sounds "augmented" but who generally eschewed the Whole-Tone like the plague lest he legitimatize the charge of copycat constantly being hurled at his head by the Debussyites, felt the harmonic and melodic color of the scale. To this date, however, the set remains relatively unexploited except in its serial state.
The number six yielded two symmetrical formations, both of which work well as controls. The 8-Tone scale—the Octotonic—is another such construction, based on the superimposition of diminished seventh chords. These being three in number—not counting inversions—there are three transpositions of the scale. A tetrachordal analysis shows it to be a "depressed" Dorian, with a semi- rather than a full-tone disjunction.
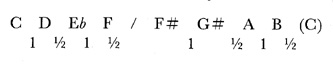
Observations
1) The scale is symmetrical, turning on 4 axes positioned a minor 3rd apart; the axes are the lower notes of the minor 2nds.
2) Any given transposition contains 4 major and 4 minor triads (plus minor 7th). There are 4 dominant complexes which include minor and aug. 9ths, augmented 11ths and major 13ths.
3) All three transpositions are related through common diminished seventh chords; simultaneous or consecutive use of any two transpositions results in chromatic saturation.
4) All intervals are represented, but there is no possibility of an augmented triad.
This is perhaps the most valuable of all scales discussed in terms of total control. Although Debussy was likely the first composer to use it in this sense in his 2nd book of piano preludes ("Brouillards," bars 32-37, "Feuilles Mortes," bars 25-30; "Les Feés sont d'exquises danseuses," bars 58-66), Ravel could dispute the claim of discovery on the evidence of the first two measures of the 4th waltz of Valses nobles (1911). As a matter of fact, Ravel here is a considerable step ahead of both Debussy and the Stravinsky of "Jeu du Rapt," both of whom regarded the complex (if, indeed, they saw it as such) rather simplistically as a superimposition of major triads a minor third removed.
There are indications that certain harmonically-advanced 19th century composers felt the symmetry of the 8-Tone: Chopin, F-minor Ballade, bar 12 of the coda; Brahms, Opus 118, No. 1, bars 5-6. In both of these instances the scale is gapped and the context tonal. Moussorgsky moved a step closed with a tritone overlay of major triads in Boris Godunov, and a case can be made for an 8-Tone construction in Wagner's Tristan progression (try combining the cadential bars, 3 & 7). Twentieth-century examples abound, an excellent one for study being Bartok's Music for Strings, Percussion and Celeste, 2nd movement, bars 186-242. And for those interested in Stravinsky's extensive employment of the scale, Mr. Berger's article is, as he would say, "a veritable primer."
II
There are two general compositional approaches to scalar control, one harmonically dynamic, the other static. The former, in which scalar colors are attached to functional (or quasi-functional) root movements, generally leads to a phrase-grouped, repetitive form; the latter, in which a single scale acts as a more-or-less complete control for a given unit of composition, results in a structure best described as cellular/additive.
The dynamic approach is excellently illustrated by Ravel's Forlane from Le tombeau de Couperin. In the space of four bars no less than four different controls are used, all attached to a root/bass progression designed to keep the phrase tonally directed despite a high degree of non-functional chromaticism. (See Ex. 11.)
Ex. 11

The key to the phrase is the augmented triad, which is used to hook together two conjunct transpositions of the 6-Tone Chromatic, the melodic minor (Overtone 5) and the harmonic minor. Bar one is clearly 6-Tone (the 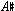 is harmonically insignificant); in bar two the
is harmonically insignificant); in bar two the  augmented triad tied over from the first measure conjoins with a new position of the scale, which is completed in the second half of the bar by the augmented triad on A. It, in turn, overlaps with notes 3, 5, & 7 of the
augmented triad tied over from the first measure conjoins with a new position of the scale, which is completed in the second half of the bar by the augmented triad on A. It, in turn, overlaps with notes 3, 5, & 7 of the  melodic minor on the 2nd beat of measure two. The latter half of bar three is clearly
melodic minor on the 2nd beat of measure two. The latter half of bar three is clearly  harmonic minor inverted at the 4th degree. Bar four moves through another harmonic minor on B, gapped, significantly, by the loss of its third degree, taking away its augmented capability as the modal cadence is approached.
harmonic minor inverted at the 4th degree. Bar four moves through another harmonic minor on B, gapped, significantly, by the loss of its third degree, taking away its augmented capability as the modal cadence is approached.
The melody, one of Ravel's most elusive, might never have been written without this particular dynamic conjunction of controls. It is unlikely that it would have been conceived in strictly linear terms, detached from its scalar environment, or as a construction growing out of a set of functional harmonies. The 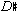 and
and 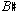 in bar 2 operate melodically in much the same way as does the augmented triad harmonically. While the
in bar 2 operate melodically in much the same way as does the augmented triad harmonically. While the 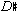 relates to the initial 6-Tone and anticipates the arrival of the melodic minor in bar 3, the
relates to the initial 6-Tone and anticipates the arrival of the melodic minor in bar 3, the 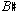 pays homage to the new 6-Tone in bar 2. A kaleidoscopic continuity is thus achieved as the color wheel turns.
pays homage to the new 6-Tone in bar 2. A kaleidoscopic continuity is thus achieved as the color wheel turns.
A second type of dynamic approach is seen in Debussy's L'après-midi d'un faune, bars 57-62.
Ex. 12

The analysis shows a descending superscale cast over a two-octave span, forcing a seemingly modulatory chromatic root progression which comes back to its Lydian center through the Neapolitan relationship. The scales are connected by two overlapping segments:7 1) the whole-tone tetrachord of the Lydian, which modulates easily to the Whole-Tone scale, and 2) the three-note unit, A
 , which is common to the two referential groups containing the melodic minor on
, which is common to the two referential groups containing the melodic minor on  and the Overtone on B; the melodic minor on A and the Overtone on D. The G-natural is interpolated because it appears in the flutes and clarinets in the repeat of the phrase at bar 63; the sound is clearly Lydian. During the entire middle section of L'après-midi, bars 31-79 (40% of the entire work), Debussy uses only scalar roots in the bass voice, on one occasion avoiding an obvious chromatic descent in order to keep intact the bass/root synonymy (see c.b. and cello lines, bars 46-47), certainly a clear indication of the extent of scalar control and color in this ingenious piece.
and the Overtone on B; the melodic minor on A and the Overtone on D. The G-natural is interpolated because it appears in the flutes and clarinets in the repeat of the phrase at bar 63; the sound is clearly Lydian. During the entire middle section of L'après-midi, bars 31-79 (40% of the entire work), Debussy uses only scalar roots in the bass voice, on one occasion avoiding an obvious chromatic descent in order to keep intact the bass/root synonymy (see c.b. and cello lines, bars 46-47), certainly a clear indication of the extent of scalar control and color in this ingenious piece.
The static approach is best seen in the Rite of Spring. The analysis which follows includes score numbers 24 through 36, a section of 82 bars. For purposes of clarity I will refer to each score number as a unit, which, indeed, it is in a formal sense. The four-note ostinato, 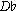 ,
,  ,
,  ,
,  , which immediately precedes the "Augurs" in unit 12 is present during the entire section, dropping a semitone in pitch at 31 to fit the two controls used in units 31 through 36. Another recurring element, appearing in all but three of the units, is this tune based on a major pentachord:
, which immediately precedes the "Augurs" in unit 12 is present during the entire section, dropping a semitone in pitch at 31 to fit the two controls used in units 31 through 36. Another recurring element, appearing in all but three of the units, is this tune based on a major pentachord:
Ex. 13
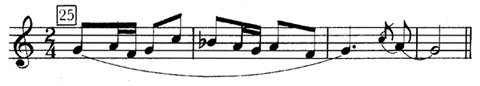
Scales consonant with this melody are limited in number. Both the harmonic minor, which heralds the "Augurs" (unit 13), and the 8-Tone accommodate the four-note ostinato but not the pentachord. The only choices are 1) one of the church modes and 2) the Overtone. Stravinsky proceeds:

Observations
1) Stravinsky is remarkably smooth in his modulations, the first three controls differing by only one pitch as the change is made. There is an abruptness only at 31 following a rather disordered transitional unit; but when the control changes at 32 there again is but a one-note variance.
2) Midway through unit 28 a block chord (in 4/3 position) attached to a melody based on the upper Dorian tetrachord appears and, along with the 6-note bass ostinato, provides the final element in a quasi-isorhythmic, quodlibetan assemblage of motives reminiscent of the final movement of the Jupiter. All of these are cast inside the Dorian on E-flat, the only non-scalar items in the entire fabric being the inconsequential trill and grace notes in the bassoons and strings.
3) The extended F-Overtone section (units 32-36) is a sudden onslaught of nine planes of action, all rigidly set inside of the control with the exception of the flutter-tongued, chromatic flourishes in the upper winds. This is perhaps the most scalar of all of the units in this section, the strings laying bare the various seventh chord configurations of the Overtone in a constantly-running pattern and the horns refusing to budge from an alteration of seventh chords based on the 3rd and 2nd degrees.
One popular textbook describes this F-Overtone section: IV7/V7 in C minor. C minor as a tonality is nowhere in sight, let alone subdominant and dominant functions! The "Augurs" closes with a typical stroke of the meat axe, and Stravinsky is off on an 8-Tone excursion in the "Jeu du rapt." Never has a compositional technique more dictated a formal result.
III
JAZZ
Scalar technique arrived on the jazz scene in earnest in the late 1940's, a not surprising occurrence given the similar developmental patterns of jazz and serious music.8 The "bop" style of that era roughly parallels that of the early 20th century in serious music, each, in its own way, representing a reaction against an over-blown, chock-full-o'-notes, romantic sound: Wagner, Mahler, and Strauss on the one hand, Stan Kenton et al on the other. Linear counterpoint took a back seat to overstuffed homophony. Symphony orchestras grew astronomically, and the original six- or seven-piece dixieland band of the jazz baroque was sectionalized (Mannheimed?) in the classical '30s and extended past the point of linear maneuverability in the following decade.
Despite their numerous shortcomings, the big bands put it all together harmonically, reaching, as did the 19th century, a set of comprehensive 13th chords based on the three basic 7th-chords. It didn't take much imagination on the part of the linear-oriented bopsters to reduce these complexes to scalar formations: the Overtone, Lydian and Dorian. Nobody worried much about theoretical niceties; it was a plain and beautiful case of empirical rediscovery of scales as the essential material of melody and harmony. The Overtone (to this day I do not know if this configuration has been given a name by jazz musicians) was particularly valuable. In addition to its two dominants, it was seen to contain all of the off-beat sevenths: the half-diminished, the minor/major and the augmented/major. Thus, a melodic burst inside the scale could serve any of four masters depending on the harmonic context. The dominant function, already well-served by the Overtone, was multiplied coloristically by the adoption of the Whole-Tone and what was referred to in some advanced quarters as the "diminished seventh" scale—the 8-Tone. The latter provided a theoretical basis for a set of dominant substitutes at the tritone and minor third which became the cornerstone (along with the iiVI syndrome) of a new harmonic style.
Melodically, the bop musician, with his ravenous appetite for notes (one had to think in eights, twelves and sixteens in order to survive), took to scales almost in self defense, predictably following the same paths of discovery as did his serious counterpart earlier in the century. Charley Parker and Dizzy Gillespie, two of the founding fathers, raised in the tonal language of "swing," supplied a new rhythmic phraseology and flow but generally confined their structures to variations on well-known standards.9 The chart in Ex. 14 shows a translation of George Gershwin's "The Man I Love" into scalar terms.
Ex. 14

Any competent bop soloist has a similar chart for his entire literature burned into his head and fingers, as well as the split-second ability to extract from it any pitch contour he feels the urge to play. As performed by the top soloists, such improvisation ranks alongside that of legendary masters of the Baroque. Each style has its problems, but each has its solutions, its technique.
The static approach, a natural outgrowth of the dynamic, was to follow a decade later, rather tentatively at first in the frenetic work of Ornette Coleman, who retained a feeling for the basic phraseology of bop, and then in earnest in the hands of John Coltrane, who was as important a figure to his generation as was Arnold Schoenberg to his. Coltrane's very musical existence was wedded to the scale. The process, as in the Rite,10 was simple: pick a scale and milk it dry. The minor church modes were particular favorites as they all have the flatted third and seventh, a sine qua non of all jazz improvisation. The Pentatonic was re-vivified melodically as it presented a neutral, gapped scale which allowed for unobtrusive changes of mode (Coltrane's "Transition" is an excellent example of this). And, of course, the blues scale—I should say "scales," as there are different varieties—suspended statically over the supporting IIVV harmony, provided grist for the wildest imaginable flights of fancy.
With this inordinate emphasis on scale, functional harmony came a cropper, ceasing to be an organizational factor, a boon to the weak-eared but rhythmically talented. I have heard some of my theory students who could quite literally not recognize a simple cadential progression perform seemingly endless static improvisations on practice room pianos, and appear quite competent in doing so. Coltrane, however, raised the style to the level of art.
Arthur Berger has expressed the hope that a new branch of theory will some day provide the key to Stravinsky's pre-dodecaphonic compositions.11 I would modify this to include all of that music currently in a theoretical limbo bounded on one side by functional tonality and by serialism on the other. It is my hope that the approach discussed here may contribute to that new perspective.
1College Music Symposium, 13 (1973), pp. 65-69.
2In 20th Century Harmony (New York: W.W. Norton, 1961), Vincent Persichetti lists several of these scales under the heading, "Synthetic Scale Formations" (Ex. 2-21, p. 44), a catch-all category including, among others, the Overtone (which is about as synthetic as a blade of grass) and the 8-Tone. He wisely accords the principle of inversion to all scales, but in assigning names he sometimes fails to identify the scale with its referential group. Thus, he refers to the 4th position of the Overtone as the "Super Locrian," and although he identifies the "Hungarian Minor" (the Gypsy) as the 4th mode (position) of the "Double Harmonic," he fails to recognize the "Oriental" as also being a member of the same referential group. Too many names only add to the already confusing array of sets.
3"Problems of Pitch Organization in Stravinsky," Perspectives of New Music, Vol. 2, No. 1 (Fall, 1963), p. 22, Princeton University Press.
4Parallel modality implies different modes (scales) with a common root tone; relative modality would describe a single referential group with different tonics.
5Messiaen inexplicably overlooks the 6-Tone Chromatic in his Technique of my Musical Language (Paris: Alphonse Leduc, 1944), Ch. 16. His "mode-3," a nine-note complex, does produce three different augmented triads, but this would appear secondary to his main structural premise: the conjunction of three symmetrical tetrachords.
6See George Perle, Serial Composition and Atonality (Berkeley: University of California Press, 1962), Ch. 7.
7The segmental overlaps which occur among the various scales are an important factor. The modes, of course, are 100% overlapped; the other scales to a lesser extent, perhaps the most important segments being the 1, ½, 1, ½, 1 cell connecting the Overtone and the 8-Tone and the 1, 1, 1, 1 common to the Whole-Tone and the Overtone. Another important cell (non-consecutive notes in some cases) found in all of the non-modal group with the exception of the Whole-Tone is the three-note unit consisting of a semitone and an augmented-2nd (½, 1-½). This could well be the most significant connection between scalar theory and serialism.
8The parallel paths of serious music and jazz (the latter compresses c. 4000 years into a scant 100) leads one to speculate as to the sequence of discovery inherent in the Western chromatic system.
9The first well-known bop piece was "Groovin' High," a chaconne-like variation. on an old tune, "Whispering."
10Hubert Laws's rendition of the Rite of Spring, CTI 6012, June, 1971, captures the essential static quality of the work and is eloquent testimony to the technical similarities between the jazz and serious approaches to scalar control.
11"Problems . . . ." p. 42.


