Modern musicians generally employ the term harmony in reference to the structure, function, and interrelationships of simultaneously combined musical tones. Thus narrowly defined, the term serves as part of a highly specialized, technical vocabulary which ignores as irrelevant to the discipline of music, the rich meanings—profoundly religious, philosophical, and psychological—of the word harmony.
The separation between practical and philosophical notions in accounting for musical phenomena is not confined to modern students of music, though the almost total neglect of the philosophical may be. Indeed, the dichotomy is very old and ultimately derives from the Aristotelian division of all knowledge into philosophia theoretica and philosophia practica.1 The result of such a division was to create the basic categories and subcategories of knowledge that suited particular modes of thought and various classes of scholars and students. The inevitable concomitant was a series of discrete treatises expounding only fragments of the body of musical knowledge in very specialized ways often as if practical and speculative matters constituted different subject areas designated on the one hand for musicians and on the other for philosophers.2 The Renaissance inherited this tendency and, of course, contributed to it. At the same time, during the sixteenth century, it became not at all uncommon for a single author to produce separate volumes on the practical and speculative or philosophical aspects of music. Implicit in this approach was the belief that knowledge of the one was essential for a full understanding of the other.3
The most successful attempt to treat the entire range of musical knowledge as an organic whole, however, came from Zarlino whose Istitutioni harmoniche4 of 1558 remains the single most important musical treatise of the Renaissance. His intention of uniting speculative, philosophical, and practical considerations is clear for, as he explains:
Theory without practice is of little value . . . , for music does not consist only of speculation. Thus, the latter without the former is truly imperfect, and this is obvious. Yet some theorists have wished to treat of some matters in music without considering actual practice and have spoken nonsense and committed a thousand errors. Similarly, others have wished to rely only on practice without the understanding of reason and have perpetrated in their compositions thousands upon thousands of follies. . . .5
Nonetheless, the efforts of Zarlino and others6 to create an organic whole of the speculative and practical aspects of music were not totally successful. One difficulty lay in weaving the numerous discrete, often contradictory, and even irrelevant threads—representing the several approaches and levels inherited from previous writers and periods—into a complete fabric. In this, no single author could succeed; for, in spite of broadly humanistic training and wide-ranging interests, no one was qualified in equal measure to handle all of the requisite considerations: metaphysical, theological, ethical, historical, mathematical, acoustical, analytical, compositional, practical. Nor were many musical writers of the period sufficiently trained linguistically to explore early Greek sources, an embarrassing lack considering the ultimate source of most philosophical views.7 At the same time, the tools for musical analysis, necessary to present an accurate picture of contemporary practice, were only beginning to emerge. Finally, and obviously, one must concede that then, as now, the theoretical approach to writing was strongly influenced by the theorist's own interests and prejudices, as the polemics of sixteenth-century musical writing quickly reveals.
In the area we have chosen to investigate—the sixteenth-century conception of harmony—the problem is further compounded by two additional considerations. The first is simply the lack of any precise organization in presenting the innumerable practical and philosophical concepts which seem to be understood under the term harmony. The second arises from the difficulty encountered by the modern reader in determining the exact meaning of the word harmony in a given context. Of one thing we can be sure: very seldom is the term used in sixteenth-century writing as it is most commonly employed today, that is, to refer to the structure, function, and interrelationships of chords.
THE THREE PRINCIPAL COMPONENTS IN THE SIXTEENTH-CENTURY CONCEPTION OF HARMONY
From the seemingly endless variety of contexts in which the word harmony appears, it is possible to extract three principal components which were central to the conception held by musical theorists in the sixteenth century.
The first component: harmony as the combination of separate and discrete entities
The first and most fundamental notion, deriving from the original Greek meaning of the word,8 is that two or more separate and distinguishable entities may be joined together in such a way that a higher order results. Thus Aristotle wrote: "We enjoy harmony, because it is a mingling of opposites which bear a relation to each other."9 To this may be added Cicero's observation that "perfect agreement and harmony is produced by the proportionate blending of unlike tones."10 Such ideas were from very early times applied to all structures, musical and otherwise, which were believed to demonstrate the unification of disparate elements into an organic whole, though most successfully to musical tones where the process and results were both observable and measurable.
The task of tracing this notion through antiquity, the Middle Ages, and into the Renaissance would not be difficult though perhaps tedious and not germane to our main point. Suffice it to say that all sources where the subject is discussed are inevitably based, implicitly or explicitly, on this fundamental idea.11 Indeed, our own present day use of the term in reference to vertical sonority or chord structure is ultimately derived from this meaning.
During the Renaissance, the basic idea of separate parts compatibly joined received explicit expression in a number of definitions, at once simple and profound. We read in Zarlino that
in general . . . music is nothing more than harmony. We can say that it is that give and take postulated by Empedocles from which, according to him, all things are generated. That is to say, it is a discordant concord, or concord of diverse elements which may be joined together.12
Similarly, counterpoint is described as
that concordance or concent which emerges from a body consisting of diverse parts and diverse modulations [melodies] accommodated to a cantilena arranged in tones which are separated from one another by measurable and harmonic intervals. . . . One could also say that counterpoint is a type of harmony which contains in itself diverse variations of tones . . . , or that it is a certain artful union of diverse tones reduced to concordance.13
On the very lowest level at which our first component of harmony is applicable, the interval, Zarlino writes:
consonance is the combination of a high and low tone which sweetly and uniformly comes to our ear. . . . It arises when two different tones . . . are joined concordantly in one body.14
Logically, then,
dissonance, the opposite of consonance . . . is the combination of a low and high tone which harshly comes to the ear. It emerges in such a way that while such tones wish to unite with one another, nonetheless, because of the disproportion between them, they are forced to remain independent; and since they offend one another, they strike the sense of hearing sharply.15
The quotations above stress the factor of compatibility or agreement in parts which are joined. Equally important, however, was the notion that the parts to be joined had to be different. Observe Zarlino's description of the unison:
Every consonance is found between two separate tones, one high and one low, making an interval . . . ; however, because the unison does not have these qualities, it can not in any sense of the word be called either a consonance or an interval.16
This point of view was extended to apply to the distinction made between what Zarlino called harmonia propria and harmonia non propria. The former, the accepted mode of sixteenth-century composition, comprised a diverse combination of consonant and dissonant intervals, and was much preferred to the latter, which consisted only of consonances.17
Also most interesting in this regard are the reasons given for the prohibition of parallel perfect intervals in musical composition:
The ancient composers forbade the use of two [parallel] perfect consonances of the same genus . . . for they knew very well that harmony results only from things which are diverse, discordant and contrary rather than from things which agree in every particular. Since only from such variety does harmony emerge, it is necessary in music that the parts of a cantilena be distinct from one another not only in their pitches but also in the direction of the modulations and in the various consonances formed of diverse proportions. And the more "harmonious" a cantilena, the more it will contain diverse movements, proportions, and distances between its parts. Perhaps the ancients saw that consonances used as I have described them18 (even though varied in pitch) were similar in procedure and in the form of their proportions. Since they recognized that such similarity did not generate variety in the concent and judged (correctly) that perfect harmony consisted in variety . . . they did not permit parallel motion between two or more perfect consonances formed of the same proportion without an intervening interval.19
The second component: proportion as the governing factor of harmony
Since it was believed that discrete entities, wherever compatibly joined, produced harmony, it is obvious that the range of harmonious structures extended from the simplest geometric forms to the universal order embodied in the cosmos. It is also clear that within the infinite number of such structures music was to occupy a special position. This occurred, no doubt, by virtue of the conspicuously agreeable sensations produced by the compatible joining of tones, which are the separate and discrete entities of music. Then, too, the opposite approaches to analysis—that is, from the separate components to the harmonious whole, or from the harmonious whole to the separate components—could be applied most successfully to intervals, the smallest and most basic unit of harmony in music. Moreover, music afforded the possibility of precise and exact measurement by direct reference to the vibrating strings which produced sound. Thus it was that for at least 2000 years following Pythagoras, comparison of string lengths, efficiently expressed in numerical ratios, became the stuff of systematic musical investigation. The process by which these studies were pursued and the conclusions drawn from them afford us an invaluable insight in determining the role of proportion in harmony. The investigator of such matters began by
first of all taking the instrument on which the material, that is, the strings, is prepared.20 Then, proceeding to the desired end, he introduces on the strings the form of a consonance and reduces the strings to a certain length and tuning, placing between them a proportionate distance and stretching them in such a way that when he plucks them, they render a perfect concent and the highest harmony.21
Thus using the ear he aimed to produce by "tuning and stretching" the agreeable sensations which must have initially obtained for music its unique position among harmonious structures. Of course, when the senses were introduced in this manner, it became obvious that all intervals were not equally agreeable, or to state it in musical terminology, equally consonant. At the same time it was also readily observed that the most agreeable or consonant intervals were defined by the simplest ratios, that is, by those which, when reduced to their lowest terms, were comprised of the smallest numbers. Hence, the explanation of the octave as the consonance which is "foremost among all others" because "one cannot find a proportion preceding the dupla," 2:1, which "is its true form."22
It is, of course, because of this connection between sound and proportion that music had a long standing within the mathematical disciplines of the quadrivium (arithmetic, geometry, astronomy, and music). It is also because of this connection that the proper subject of the science of music was considered to be "number [or proportion] and tone" which, taken together, were called the "sonorous number" (il numero sonoro).23 Most instructive, therefore, will be the explanations which attempt to account for this association of tone and number more fully. In his efforts to understand this phenomenon, Zarlino turned to Aristotle's "four causes" and adapted them in the following manner:
. . . the purpose of an action . . . , for example, the playing, entertaining, or delighting in harmony . . . , is called the final cause; the agent, that is, the musician . . . , is called the efficient cause; the material, which consists of the strings, is the material cause; and the form, that is, the proportion, is called the formal cause. Nonetheless, the last two are intrinsic causes of a thing while the agent and purpose are extrinsic. Thus the first two causes do not pertain to the nature or existence of a thing, while the last two are essential parts of it because every perishable thing is composed of material and form. The material is that substance of which a thing is made and is inseparably a part of it, like the tones [for example] which comprise consonances. The form is that species, likeness, or, if we wish, example, which holds the thing in itself, by which it is identified, like the proportion of a consonance. And this is called the intrinsic cause to differentiate it from the extrinsic. It is, so to speak, the model, or, if we wish, the example, in whose likeness a thing is made. In this sense, the proportion of number to number is the model for consonance.24
It is obvious from the above explanation that the word "cause" in the Aristotelian usage which Zarlino accepted had much broader connotations than we normally associate with the term; it embodied purpose (final cause), activating agent (efficient cause), substance (material cause), and essence (formal cause). Aristotle's aim was to provide a series of philosophical tools leading to a full explanation of an object: Zarlino's adaptation seems to imply a reasonable grasp of this intent. Still, there must have been an irresistible temptation to assume for proportion not the mere utility of a tool for describing the philosophical essence of intervals—whatever that would mean—but the cause (in the modern sense) which produced the harmonious effect. Thus, it is difficult to read the statement that "proportion is the formal cause of consonance" which "regulates and puts vibrating bodies into proper relation"25 without believing that Zarlino literally meant cause and effect. We reach a similar conclusion when we note Zarlino's reference to mathematics as "the master of all cantilena,"26 his statement that "number is inseparable from consonance,"27 his belief that "proportionate" tonesthat is, tones exhibiting a proper relationare the material of music,28 or his association of dissonant tones with disproportion.29 The inevitable conclusion, therefore, is that the sixteenth-century theorist literally believed that the euphonious effect of musical intervals was caused by proportion.
The third component: a hierarchy of harmonious structures
The significance of numbers applied to consonant intervals does not end with the cause and effect relationship which we have noted. Proportion had a universal meaning which Zarlino recognized as follows:
. . . from the first origins of the world, all things created by God were given order by Him through numbers (as one obviously can see and as the philosophers affirm). Indeed, number was the principal model in the mind of the Creator. Thus it is necessary that all things which are separate or together are composed of number and subject to number. So necessary is number that if it should be taken away, everything would be destroyed, and (as Plato says) man would lose his wisdom and knowledge because nothing in his intellect or memory could restore reason. The arts would be lost; nor would there be any need to speak or write about music because its reason would be nullified since it would not have the great support which comes from numbers.30
Of course, such ideas were ultimately derived from Greek antiquity as Zarlino acknowledges in his reference to Plato. Indeed, it is interesting to compare Zarlino's explanation with the account given by Aristotle:
The so-called Pythagoreans applied themselves to mathematics, and were the first to develop this science; and through studying it they came to believe that its principles are the principles of everything. And since numbers are by nature first among these principles, and they fancied that they could detect in numbers . . . many analogues of what is and comes into being . . . ; and since they further saw that the properties and ratios of the musical scales are based on numbers, and since it seemed clear that all other things have their whole nature modelled upon numbers, and that numbers are the ultimate things in the whole physical universe, they assumed the elements of numbers to be the elements of everything, and the whole universe to be a proportion or number. Whatever analogues to the processes and parts of the heavens and to the whole order of the universe they could exhibit in numbers and proportions, these they collected and correlated.31
Thus was established the supreme faith in number as an organizing force which prevailed almost to modern times.
But if all harmonious structures were ultimately reducible to number, it also followed as a corollary to Pythagorean belief that all orders were basically similar. The proof of this, as Aristotle's summary indicates, resides in the relationship between musical intervals and the proportions which governed them. For if in this one, easily observable instance, the harmony of a musical interval—let us say, the octave—clearly reflects the "harmony" of a simple ratio—2:1—then by extension and analogy, all harmonious structures must be similar, even where such similarity is not provable. And with the notion that the "harmony" of a proportion is of a higher order than the harmony of an interval"for the form is nobler than the material"32—a hierarchy is established which, again, by extension and analogy, encompasses all harmonious structures. Thus the belief developed that music was but a reflection of higher, inaudible harmonies, a microcosm within a macrocosm whose prototypes were man, the universe, and God. As a subject for serious philosophical study, then, music's value was universally assured. The thirteenth-century philosopher, Roger Bacon, affirmed that by the study of numbers in music does man comprehend the "invisible things of God." Quoting Augustine, he stated that "not a few things in the sacred books an ignorance of the principles of music closes and covers up."33 It is within this context that one is to understand the significance of Boethius' appropriation of musical terminology to carry out the implications of his belief in a hierarchy of three levels: musica instrumentalis (the harmony of audible musical sounds), musica humana (the harmony of the human soul and body), and musica mundana (the harmony of the universe, the so-called "music of the spheres").34
Obviously, then, the full implications of a hierarchy of harmonious orders reached to the profoundest depths of man's understanding, and we cannot leave this component in our discussion of harmony until we explore two additional items which bear directly upon it. The first deals with the unique position of music within the hierarchy and the special problems that derive therefrom; the second attempts to explain the emotive power of music.
The imitation of nature
If music held a unique position within the hierarchy of harmonious orders, it also, for the same reason, bore the clear responsibility of accurately mirroring these orders. However, beyond the point where the harmonious interval reflected the "harmonious" proportion, the implementation of this idea was patently difficult, if not impossible. Consider, for example, the "rules for fitting songs to the heavenly bodies" given by Ficino:
1. Find out what powers and effects any particular star has in itself, what positions and aspects, and what these remove and produce. And insert these into the meaning of the text, detesting what they remove, approving what they produce.
2. Consider which star chiefly rules which place and man. Then observe what modes and songs these regions and persons generally use, so that you may apply similar ones, together with the meaning just mentioned, to the words which you wish to offer to these same stars.
3. The daily positions and aspects of the stars are to be noticed; then investigate to what speech, songs, movements, dances, moral behaviour and actions, most men are usually incited under these aspects, so that you may make every effort to imitate these in your songs, which will agree with the similar disposition of the heavens and enable you to receive a similar influx from them.35
To most sixteenth-century musicians, these suggestions, insofar as they gained any currency,36 probably appeared as far-fetched then as now. Indeed, the whole concept of musica mundana was a difficult one which even musical theorists scarcely comprehended. Tinctoris, for example, placed no credence in a "music of the spheres,"37 while Zarlino more cautiously cited Cicero's explanation that the inaudibility of such sweet sounds was the result of the human ear not being "capable of comprehending the sweetness of celestial harmony for its excellence and grandeur."38 Nevertheless, it must not be assumed on this account that the hierarchy of structures, capped by cosmic music, was rejected. The notion of universal harmony, far too cogent to be completely dismissed, was given expression, instead, in a rather naive view of natural order. Even here, however, we encounter several difficulties, chief among them the lack of a generally accepted definition of the term "nature."39 For musicians, however, the frequently encountered call to "imitate" nature meant not its sound or appearance, which in music was manifestly impossible,40 but its inherent order, exhibiting proper proportion and, if we rightly understand the word "proper" in this context, moderation. This was described as follows:
When the ancient philosophers, the keenest and most careful investigators and discoverers of things, were considering the effects produced by Mother Nature in the upper and lower worlds, they recognized that the motion of the heavens was inviolate and never intruded upon nor impeded; that the sun always followed the same course without ever stopping; that the moon similarly proceeded with equal order; that day did not take the place of night, nor night that of day. They observed that winged animals remained in their own region, which was the air, and did not enter into places meant for fish, and that fish did not leave their confines; that each distinct tree did not produce the fruit of another, but in accordance with its own species produced that which was preordained by nature; that grape vines did not make apples or pears, nor did oak trees produce grapes; that the earth observed the manner of producing green plants. Thus, marvel at such order, for through it one thing is differentiated from another, thus avoiding pernicious confusion.41
In other words, each thing in its proper place. It is perhaps with this explanation in mind that Artusi urged that "art ought to imitate nature in its operations as much as possible," adding that to accomplish this "it is necessary to have a certain proportion, or moderation lest it [art] be disdained and abhorred by our senses."42 The shift to natural order as the model for musical order, of course, solved no problems at all, as we can see in the following attempt to apply the principle in practice:
Let us permit as a universal rule that since in diminished counterpoint,43 the consonances are used in places ordained for them by nature (which gives order not only to animate things, but also to inanimate things) . . . , and in this way we proceed from one interval to another which is closest to it, as determined by nature . . . , so also in the use of dissonance must we proceed in similar manner. Thus after a dissonance there follows that interval which has been determined and given its place by nature; and it will be the one nearest to the dissonance.44
Artusi then proceeds to outline more specifically what he means. For consonant intervals, he instructs, the octave follows the major sixth, the fifth follows both the minor sixth and the major third, the unison follows the minor third. For dissonant intervals, the third succeeds both the second and the fourth, and the sixth succeeds the seventh.45 All of which seems clear, logical, and perhaps a reasonable means for the composer to "imitate" the order inherent in nature, until we observe Artusi conceding that the prescribed procedures "permit many exceptions."46 It would seem, then, that the references to natural order in Artusi's passages are merely parallels to the procedures literary theorists were accustomed to follow. According to one authority, "such equivocal terms as 'nature' and 'natural' . . . [were] sometimes used as little more than authoritative or derogatory sounds, or arbitrary shifts for lending weight to the particular argument a writer has in hand."47
The ethical effects of music
If the notion that harmony embodied a hierarchy of structures all basically similar led to the belief that music should imitate natural order, then by a similar line of reasoning the same idea helped to explain the ethical powers of music. Long recognized by theorists and philosophers, these powers were summarized by Zarlino as follows:
[Music] excites the mind, moves the affections, mitigates and pacifies fury, makes time pass virtuously and has the power of generating in us a life of good, especially when it is used in the proper manner and moderation. . . .48
To this broad spectrum, originating with the ancient Greeks, is added the traditional Christian view that through music man "praises and thanks the Creator,"49 at the same time refreshing the spirit and reducing oneself "to the contemplation of celestial things."50
How these ethical powers of music took effect is explained by the belief that man, created in harmonic proportions, delights in the similar harmonic proportions of actual music. Or, in the terminology adopted in this paper, one structure in the hierarchy of structures affects other structures because of the basic similarity between them. Thus, concludes Zarlino, "the person who is not composed in harmony does not delight in music."51 It is through this similitude, therefore, that emotional states are induced by music:
Thus we can say that these same proportions that are discovered to be the cause of anger, fear, or any other passion . . . are found also in harmony; for similar proportions are the cause for exciting similar effects.52
Furthermore, Zarlino concludes, the susceptibility of a person to a specific emotional state is increased by that harmony which is "similar in proportion" to the emotion:
For, according to Boethius, similitude is friendly to everyone and diversity is contrary and odious. If [on the other hand], it should happen that one hears a [harmony] of diverse proportion, such passion diminishes and a contrary one is generated. One may say, therefore, that such a harmony purifies the passions of whoever hears it by the deterioration [of one passion] and the generation of another contrary to it. This is evident when someone who is disturbed by some passion which comes from sadness or from the rising of the blood, like anger, hears a harmony of contrary proportion containing some pleasure; for then the anger in him ceases and deteriorates and immediately a gentle passion is generated. This also may occur with other passions, because everyone naturally delights more in that harmony which is most similar, appropriate, and proportionate to his nature and constitution and according to which he is inclined, than in the contrary.53
It is worth noting that the proof of the similitude between the proportion of a harmony and the proportion of an affection is again made by analogy and extension of an observable property of the musical interval. The explanation is given by Artusi:
. . . like affects like. Have you ever seen two strings tuned together in unison or in octaves? On one of them is placed a piece of paper or a straw. Touch or pluck the other which has nothing placed on it and the paper or straw on the first will fall because of the similitude and sympathetic quality which the tones have between them. This effect will not occur on a string which is tuned differently. Thus one concludes that like operates on like and natural things on nature.54
THE CIRCULAR NATURE OF THE SIXTEENTH-CENTURY CONCEPTION OF HARMONY
With the concrete example employing the principle of sympathetic vibration to illustrate the means whereby ethical effects took place, we may see a rather neat and precise connection between the grandiose conception of a hierarchy of harmonious orders mirroring one another and the idea of separate elements compatibly combined. Both notions are rooted in the unique properties of the musical interval. Indeed, the whole philosophical conception of harmony may be viewed as a circular affair; in it the three components which we have been elaborating lead most logically from the first, to the second and third, and back once again to the first. The point of contact throughout, at once establishing the veracity of the ideas and their logical progression, remains the interval. Thus the notion that harmony was fundamentally a compatible joining of separate and discrete entities—provable by observing the agreeable effect of consonant intervals—led quite naturally, through the measurement of string lengths sounding those intervals, to the belief that numerical proportion governed that effect. Similarly, the observation that the harmony of one order, a consonant interval, was modeled on the "harmony" of another, a simple numerical ratio, led in turn to the establishment of a hierarchy of orders. Finally, with the observation that within the hierarchy one order may affect another—as proved by the vibrating string which activates a second string tuned sympathetically to it (though not a third which is mistuned)—we revert to the fundamental notion of compatibility. Of course, the circular pattern may be reversed, or, indeed, since a circle has no beginning and no end, started at any other point.
But what specifically did such notions mean in actual composition beyond investing a few technical definitions with theological, philosophical, or psychological significance? And how did philosophical conceptions of harmony relate to musical ones beyond the fact that the interval provided the necessary proving ground for some far-reaching notions? (We have already touched upon some problems in answering this last question in the quotations from Artusi relating to natural order.) And finally, what, indeed, was the sixteenth-century conception of harmony in music?
To find whatever answers there may be to these questions we begin once again with the interval. For not only did this basic musical unit provide the proofs for several philosophical concepts, it also served as the point of departure for "the speculation of every musical composition."55 Our investigation turns, therefore, to a fuller examination of the numero sonoro which we previously explained as the sounding interval considered together with its governing proportion. This concept, with its attendant philosophical ramifications, delimits the basic harmonic materials available to the sixteenth-century composer.
The Senario
One might suppose that there were as many numeri sonori as there were conceivable intervals. However, since the sixteenth century conception of harmony included the notion that separate entities had to be joined compatibly, it is clear that there was an existing criterion by which combinations of tones could be judged. And because, in addition, the sixteenth-century conception of harmony involved other ideas than mere compatibility, the practical limits on the amount of usable intervals could be set by reference to the proportionate qualities of some higher order which music was supposed to mirror. The key word in the above is proportionate: the term almost invariably meant number which was, as we have seen, the most immediate model for music. The obvious source for a limiting factor, therefore, lay in the realm of proportional mathematics. And in an ingenious manner, the theorist was able to refer to one basic mathematical entity to establish his guiding limits.
The entity adopted by most sixteenth-century writers was the number six, or more properly, the senario,56 which became the one numero sonoro governing all other numeri sonori. Considered perfect in Pythagorean reasoning by virtue of the fact that it was equal to the sum of its aliquot parts,57 the senario governed a fantastic array of phenomena, which, in turn, served to attest its marvelous qualities. The list provided by Zarlino included such "harmonious" orders as the six signs of the Zodiac in each hemisphere, the "six peregrinations of the six planets" (Saturn, Jupiter, Mars, Venus, Mercury, and the moon) through the Zodiac; the six circles placed in the heavens (Arctic, Antarctic, Tropic of Cancer, Tropic of Capricorn, Equator, and Ecliptic); the six essential qualities of the elements (acuteness, thinness, and motion, and their opposites, dullness, density, and quiet); the six natural offices "without which nothing can exist" (size, color, shape, space, order, and motion); the six possible changes of location or position (up, down, forward, backward, right, and left); the six sides of a cube; the six equilateral triangles contained in a circle; the six ages of man (infancy, childhood, adolescence, youth, old age, and decrepitude); the six modes of logical proposition (true, false, possible, impossible, necessary, and contingent); and the six feet in the verse of a heroic poem.58 The list concludes with several musical phenomena:
Six are the species of musical tones [i.e., intervals] among which are contained every musical concent: unisone, equisone, consone, emmele, dissone, and ecmele.59 Six also are the consonances considered by practical musicians, namely, five simple and elementary which are . . . the diapason, the diapente, the diatessaron, the ditone, and the semiditone, and one principal which is the unison (although this is not, properly speaking, a consonance . . . ).60 In addition, there were, according to ancient musicians, six species of harmony, namely, Dorian, Phrygian, Lydian, Mixolydian or Locrian [!], Aeolian, and Iastian or Ionian. Among moderns there are six principal modes called the authentic, and six nonprincipal called the plagal.61
The seeming naivete of the above must be understood in light of the further implications of the senario. For this one numero sonoro included the numbers 1, 2, 3, 4, and 5, as well as 6, and the proportions between any pair of them. This resulted in the numeri sonori which gave "the reason or form" for musical consonances.62 The chart which Zarlino used to illustrate this is reproduced in Figure 163 and summarized in Figure 2.
Fig. 1.—Zarlino's illustration of the consonances contained among the various pairs of numbers in the senario.
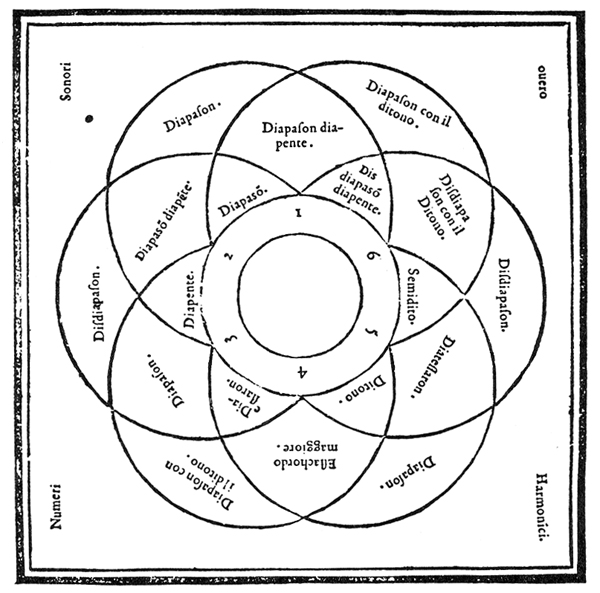
Fig. 2.—A summary of Figure 1.

In addition, the concept of the senario included the squares of its components (1, 2, 3, 4, 5, 6), as well as the products of any of its pairs. This extension further provided proportions not available within the components. Placed in "natural" ascending order, all of these numbers resulted in a sixteenth-century equivalent to the overtone series. The results may be seen in Figure 364 and Figure 4.
Fig. 3.—Zarlino's illustration of the "natural" order of consonant intervals contained among the components of the senario, and the products and squares of these components.
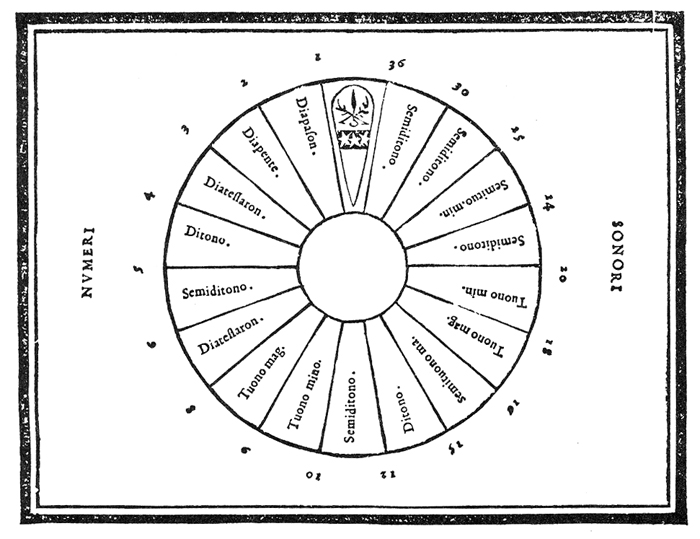
Fig. 4.—A summary of Figure 3.

"These, then, are the proportions of the numero senario and its parts," concludes Zarlino. "It is not possible to duplicate them in any other number, whether smaller or larger."65
Perhaps it is to the proportions between all of the numbers obtained from the senario that Zarlino referred when he spoke of the harmony "hidden" (rinchiusa) within the number six. In any event, it is worth noting that the proportions in the senario, and the consonances associated with them, demonstrate again how one order imitates another. By analogy, similar hidden relationships must regulate the whole catalogue of phenomena posited by Zarlino as being governed by the number six. In this light, we quote the passage in which the word "hidden" appears:
So that he [the prophet Moses], who was a perfect master of every science, and understood, through the work of the Divine Spirit, the harmony which was hidden in this number [i.e., the senario], might comprehend from visible and apparent things the invisible things of God . . . , he turned in an instant to this number and the harmony hidden in it to illustrate and express the perfection of [God's] work.66
Consonance and Dissonance
The abstractions and esotericisms involved in the discussion of the interval thus far take a more practical turn with the consideration of consonance and dissonance. Indeed, the reference to the senario as a means of limiting the number of usable intervals might more accurately be considered a way of identifying and defining the various musical consonances; dissonance, which was also a usable unit of harmony in sixteenth-century composition, can only indirectly and with some good bit of ingenuity be derived from the senario.
However, even should we confine our investigation to consonant intervals, we shall begin to see a breakdown in the close relationship of philosophical to musical conceptions which has been the basis for our discussion thus far. For the final count of allowable consonant intervals, as acknowledged by theorist and composer alike, was not completely consistent with those derived from the senario. This may be seen by comparing the following list—unison, octave, perfect fifth, perfect fourth, major third, minor third, major sixth, and minor sixth67—with the intervals given in Figure 1 and Figure 2. The unison, of course, poses no real problem, for while it is not, properly speaking, an interval, it is a "beginning" analogous to the geometric point which starts the line but is not the line itself. Hence, the unison serves as "the generator of consonances; without it no other interval can exist."68
The real discrepancy comes with the minor sixth whose ratio, 8:5, is not derivable from the parts of the senario. Since composers had long since "embraced" this interval and numbered it among the consonances,69 there was no question of its inclusion. The necessary theoretical justification was provided by adding other consonances contained in the senario, a procedure which also produced an alternate method for deriving double octaves, twelfths, elevenths, and tenths. Hence, Zarlino's explanation: "The major sixth as well as the minor comes from the addition of the fourth to the major or minor third."70 The illogicality of this procedure must have disturbed Zarlino. For if by this reckoning the minor sixth was "potentially present"71 among the consonant intervals of the senario, so, too, was the seventh by the addition of a fifth and a third. At a later point, Zarlino sought to eliminate this inconsistency by referring to another numero sonoro, the ottonario,72 but the damage had already been done. To a perceptive critic like Galilei, this need to go outside of the senario for justification of a commonly accepted interval fatally compromised the validity of the senario and the entire philosophical apparatus attached to it. We shall return to this point later when we begin to examine more critically the theoretical exposition of the compositional process.
For the moment it will be of some value to permit Zarlino to pursue his investigations of intervals to their conclusions since he was not yet at the point of quitting his deliberations on this matter. Thus, in a confusing, shifting, and often contradictory series of discussions, he proceeds to establish several overlapping categories of consonance based variously on degrees of euphony, kinds of ratios causing the interval, and various methods of computing. The results of these investigations, spread out over several chapters in two of his treatises, are condensed in Figure 5.
Fig. 5.—Categories of consonance according to Zarlino.
| CATEGORIES OF CONSONANCE | Unison | Mi 3d | Ma 3d | 4th | 5th | Mi 6th | Ma 6th | 8vo | Compounds | |
| "Beginning,"—not really an intervala | x | |||||||||
| * | "Simple"8—vo or smallerb | x | x | x | x | x | x | x | ||
| "Composed" (composta)—formed by adding two consonancesc | x | x | All compounds | |||||||
| * | Compound (replicata)—all intervals larger than 8vod | All compounds | ||||||||
| "Simple after a fashion" (ad un certo modoe) | x | x | ||||||||
| ± | "Properly so-called" (propriamente detta)—from multiple and superparticular ratiosf | x | x | x | x | Compounds of these | ||||
| "Commonly so-called" (communemente detta)—from other simple ratiosg | x | x | ||||||||
| Perfect (according to practitioners)h | x | x | x | x | Compounds of these | |||||
| Imperfect (according to practitioners)i | x | x | x | x | Compounds of these | |||||
| "Between perfect and imperfect"j | x | x |
| "More full or more empty" (più piena, più vaga)k Vague and nebulous terms which apparently refer to the size of the interval as it is closer (più piena) or further (più vaga) from the unison. |
| aIst. harm., III, xi. | gDim. harm., 84. | |
| bIst. harm., I, xiii, xiv, xv; Dim. harm., 87 (no 6ths); Ist. harm., III, iii (includes 6ths). | hIst. harm., III, vi. | |
| cIst. harm., I, xiii, xvi; Dim. harm., 87 (no 6ths). | iIst. harm., III, vi. | |
| dIst. harm., III, iii. | jIst. harm., III, vi. | |
| eDim. harm., 87. | kIst. harm., III, viii; cf. discussion in Marco, op. cit., 398. | |
| fDim. harm., 83. |
| * | These two categories are the ones with which practitioners are concerned. |
| ± | A multiple proportion occurs when one of the terms may be divided by the other with no remainder, e.g., 2:1, 6:3, 8:2. A superparticular proportion occurs when one of the terms exceeds the other by one, e.g., 3:2, 4:3, 6:5. |
In light of the full and exhaustive treatment accorded to consonance, Zarlino's discussion of dissonance is somewhat disappointing. This, of course, is completely consistent with the philosophical view of harmony which obviously demanded a more careful study of compatible combinations than incompatible ones. In effect, Zarlino's conclusion is simply that all intervals which are not consonant are dissonant, associating the harsh effects of the latter with proportions outside of the senario.73 Major seconds are derived from the distance which separates the fifth from the fourth, or the fourth from the minor third;74 similarly, minor seconds are taken as the distance which separates the fourth from the major third.75 Sevenths are regarded simply as the addition of the major or minor third to the fifth.76 Diminished and augmented intervals are generally obtained with the aid of accidentals by raising or lowering one of the tones of a perfect interval.77 Interestingly, this addition, subtraction, or modification of intervals within the senario seems to be sufficient to establish the necessary association of dissonant intervals with the senario.
Zarlino's final tabulation of consonant intervals, forming the basic harmonic unit of sixteenth-century composition, accords well with other theorists and with musical practice as it occurred in the last half of the sixteenth century:
Consonant intervals: unison, perfect fifth, perfect fourth, major and minor thirds, major and minor sixths, all compounds of these
Dissonant intervals: (perfect fourth),78 major and minor sevenths, diminished and augmented intervals, all compounds of these
Once determined, the qualities of intervals remained absolute and inviolate like the settled and predetermined order of number they purported to follow. For they "were set," concluded Artusi, "on that day many years ago when composers first began to unite parts together in modulation."79 Thus,
Even if you wish dissonance to become consonance, it remains necessary that it be contrary to consonance; by nature it is always dissonant and can hence become consonant only when consonance becomes dissonant; this brings us to impossibilities. . . .80
Even so progressive a theorist as Galilei, who disagreed violently with the viewpoint represented above, did not substantially alter Zarlino's list.81 And that out and out "revolutionary," Monteverdi, made it quite clear that he intended to "take his stand upon the consonances and dissonances approved by mathematics."82
The Sixteenth-Century Approach to Composition
The careful reader will note that throughout our discussion of harmony thus far, we have spoken not so much of music as of the interval, though at times using the former term as a kind of euphemism for the latter. Of course, intervals joined together successively are the stuff of which music is made. As a matter of fact, one is led to believe, from a study of the practical aspects of treatises, that composers regarded composition of music in this very light. Consider, for example, the roles of consonance and dissonance described by Zarlino in the following passage:
. . . every composition, every counterpoint, and—to put it in a single word—every harmony is composed principally of consonances. However, for greater beauty and charm, one also uses, secondarily and incidentally, dissonances which, although not very pleasing to the ear when used by themselves, nonetheless are not only tolerable and inoffensive to the ear, but give it great pleasure and delight. This occurs when they are employed in the proper manner and according to the precepts which we shall demonstrate. Thus, dissonances serve the musician in two important ways, among others. The first . . . is that with their aid the composer can pass from one consonance to another. The second is that dissonance, by contrast, makes the consonance which immediately follows it seem more delightful. Thus the consonance is comprehended and recognized with greater pleasure by the ear in the same way that light is more pleasing and delightful to the sense of vision after darkness, and sweetness more palatable and delicious after bitterness. This is proved by our daily experiences, for whenever the ear is offended by some dissonance, the consonance which follows it seems sweeter and more delightful. For these reasons, our predecessors decided that in composition there should be a place, not only for the perfect and imperfect consonances, but also for the dissonances. They knew that greater beauty and charm would result more with the dissonances than without them. For if a composition was comprised only of the consonances, such a piece, even though pretty and effective, would nonetheless, be somewhat imperfect . . . and lack the great elegance which comes from a mixture of consonances and dissonances. . . .83
The sixteenth-century theorist, then, regarded composition as the judicious collocation of consonant and dissonant intervals with two main functions assigned to the latter:
1. As a means for moving "from one consonance to another," that is, as a secondary phenomenon melodically induced and only incidentally discordant (passing tones and various types of ornamental tones, e.g., the auxiliary, anticipation, cambiata, etc.).
2. As an aesthetic foil for consonance (a kind of "salt or condiment for good harmony," as Artusi described it84), that is, as a primary phenomenon harmonically induced and intentionally discordant (practically synonymous with the suspension).85
Regardless of its function, dissonance inevitably required great care within the musical fabric in order to arrive at a compatible union with consonance. Explains Zarlino:
Even though I have said that in composition, we use principally the consonances and secondarily the dissonances, one should not assume from this that we may employ the latter in counterpoint or composition without rule or order, as sometimes occurs. For from this procedure confusion results. Instead, one must take care to use them with order and rule.86
The principal determinant in arranging consonant and dissonant intervals with "order and rule" was the battuta, which is roughly equivalent to our modern beat (though without the notion of regular accentuation) and comprised of a thesis and an arsis.87 Generally, the battuta was equal in time to a breve divided into two semibreves for duple time, or into three semibreves for triple time; the battuta could also be equal to a semibreve similarly divided into minims.88
Dissonance as a secondary phenomenon
The following quotation will serve to introduce the three general principles which governed the use of dissonance as a secondary phenomenon:
The contrapuntist may alternate consonant and dissonant minims [the battuta being equivalent to a semibreve] provided that the consonant one falls on the thesis and the dissonant one on the arsis and that they proceed downward or upward in strict conjunct movement.89
In other words,
1. The thesis must be accompanied by a consonance; the arsis may be accompanied by a dissonance.
2. When dissonance is employed, it is in alternation with consonance.
3. The movement to and from a dissonant tone is strictly by conjunct movement.
This pattern of treatment is also maintained for note values smaller than the whole note (with the battuta, of course, still equivalent to the whole note), except that
quarter notes falling on both the thesis and the arsis should be consonant. For this reason the first and third quarter notes [in a group of four] should be consonant while the second and fourth need not be so.90
This rule later became generally expressed as the alternation of a "good" (buona) and a "bad" (cattiva) tone.91
Practical musicians, of course, deviated from a strict pattern of alternation between consonant and dissonant quarter notes. Thus, Artusi sanctioned the use of two dissonant middle tones in a group of four quarter notes, providing the outer two were consonant. In this case, the thesis remains consonant, but the arsis becomes dissonant. Artusi illustrates his suggestion with the examples in Figure 6.92
Fig. 6.—Use of two successive dissonant quarter notes.

In general, however, the alternation of "good" and "bad" is preferred. Indeed, Zacconi goes so far as to advocate this pattern for eighth and sixteenth notes without seeming to acknowledge the necessity of greater freedom in using these "ultimate figures of diminution."93
Zarlino also observes that while generally the first of an isolated pair of quarter notes is to be consonant, there is also the possibility that "the first be dissonant providing the second is consonant."94 The examples in Figure 7 illustrate his point.95
Fig. 7.—Possible dissonant usage in pairs of quarter notes.

All of the dissonant tones permitted thus far are in the nature of passing tones (to use modern terminology) and occur on the unstressed portions of the battuta (taken as a whole note). As a matter of fact, Zarlino's commentary takes no note of any other type. However, his musical examples incidentally make use of the auxiliary. Figure 8 gives examples in quarter and eighth notes.96
Fig. 8.—Use of the auxiliary.

From the example of Figure 8, and from a free application of the principle of alternation between "good" and "bad," there is no reason to suppose that theorists did not accept other minor deviations from the stated rules. Such deviations might include the popular cambiata and similar devices where dissonance continued to serve as a secondary phenomenon. Unfortunately, the theoretical sources make no mention of these devices.97
On the other hand, the requirement that the dissonant tone be approached and quitted in strict conjunct movement receives considerable attention. Writes Zarlino:
All that I have been saying [about the ways to use dissonance] must be applied only when the parts of the counterpoint proceed conjunctly. In disjunct movement it is necessary that the notes involved in such movements be consonant with the subject.98
Such an enjoinder is completely in accord with the subsidiary role dissonance was required to play. For as Zarlino perceptively observes,
when the dissonance . . . occurs in conjunct movement . . . it is not offensive to the ear. However, in disjunct movement the dissonance is emphasized and can hardly be tolerated.99
Dissonance as a primary phenomenon
Under certain conditions the dissonance may also be placed on the thesis of the battuta. The manner of its employment and the reasons for its acceptability are described by Zarlino:
The first portion of the battuta may be dissonant when it contains the second half of a syncopated whole note in the counterpointing part; in this case, the first part of the whole note occurs unequivocally on the arsis, or upbeat [of the preceding battuta] and thus the dissonance is acceptable. For in singing such a syncopated whole note, the voice holds the tone and one hears a suspension, or almost a lack of sound, such as occurs after the articulation which begins sound and through which tones [of the same pitch] are differentiated from one another. Thus the ear barely notices [the dissonant portion of the whole note]. Because there is no articulation [at the point of dissonance], and hence the movement is weak, the ear is not moved in such a way that it can grasp [the dissonance] fully. Thus the tone, sounding through the syncopation, loses the intensity which it had at the beginning of its articulation. Insofar as the dissonance is weakened, both for having occurred on the second part of the syncopated whole note and for the more obvious movement from tone to tone in the other voice part, it is barely heard. It is noticed, of course, but it passes quickly. And if the ear is a little offended, why, then, in comparing the dissonance to the consonance which follows, it finds not only that the dissonance is not disagreeable, but, indeed, oddly pleasant. For the consonance following is thereby heard to be even sweeter and smoother. This happens, perhaps, because every contrary is best perceived and appreciated by comparison with its opposite.100
The classic treatment of the suspension, as we now refer to the procedure outlined above, may be given in the summary below:
1. The tone which is to become a dissonant suspension is introduced as a consonance on a relatively unstressed portion of the battuta.
2. It remains stationary while a dissonant relationship is formed on the next relatively accented portion of the battuta by the movement of a second voice part.
3. The suspended tone is then resolved by a descending second into a consonant tone on the next relatively unaccented portion of the battuta.101
An example provided by Zarlino to illustrate the proper treatment is given in Figure 9.
Fig. 9.—Examples of the suspension.

The suspension is usable in all sections of the cantilena but nowhere more than in the cadence which, "without dissonance, has neither grace nor charm."102 At the same time, perhaps because the contrapuntist felt obligated to show his ingenuity in cadential formations,103 a certain amount of freedom in the treatment of dissonance was permitted, usually in association with diminution. Artusi dealt with the matter at some length, illustrating his discussion with what we would call ornamented resolutions of suspensions which in their emphasis upon cadential procedures rather than upon discordant tonal combinations in no way violated the spirit of sixteenth-century dissonance treatment. Artusi's examples may be seen in Figure 10.104
Fig. 10.—Dissonances used in diminished cadences.

He makes a particular point, however, of differentiating between the procedure permitted in Figure 10c with that of Figure 11105 which is strictly forbidden.
Fig. 11.—Instances of improper (a) and proper (b) movement to a dissonant tone.

As for the movement from one consonant interval to another, the procedure seemed to be governed as much by melodic as by harmonic considerations. The aim was
to write the voice parts . . . in such a way that they are easily singable and proceed in beautiful, graceful, and elegant movements so that the listener will delight in the modulations and not be offended by any of them.106
To this end, the conjunct movements of the tone and semitone were preferred ''as much as possible."107 Also of great utility were the octave, fifth, fourth, and third. Other intervals were possible, although, curiously enough, as the century progressed, there was a tendency among theorists and composers to limit the selection, especially in sacred music, to those mentioned above.108 Thus, around mid-century, Zarlino recommended such intervals as
the tenth, which may be used without error, for that master among our predecessors, Josquin, used not only that interval but the twelfth also . . .109
He even included such possibilities as "the seventh and ninth, for although these are rare, still, they have been used and continue to be used by good composers."110 Forty years later, Artusi made it clear that such "precipitous leaps" were to be avoided.111 At the same time, he also banished the major sixth ascending or descending, and the minor sixth descending, modulations which Zarlino had not mentioned.112 Obviously, in this line of thinking, all diminished and augmented intervals were prohibited. By the end of the century, the tabulation of melodic intervals recognized by theorists was a modest one: octave, ascending minor sixth, perfect fifth, perfect fourth, major and minor third, major and minor second.
From an harmonic point of view, writing consecutive consonant intervals involved considerations of voice leading and types of consonances involved. Thus, while it was possible to write consecutive perfect or imperfect consonances "of diverse forms" (i.e., not parallel),113 it was better to alternate perfect and imperfect consonances.114 Similarly, contrary motion was preferred,115 although certain types of parallel motion (for example, from an octave on C up to a fifth on G) were tolerable if used sparingly in two-part writing and perfectly acceptable in more than two-parts.116 Especially Zarlino was quite strict in his admonitions to move from a perfect or imperfect consonance to a perfect consonance by means of the nearest interval. Thus, one should proceed from the unison to the third, from the third to the fifth, from the fifth to the sixth, and from the sixth to the octave, and vice versa.117 Further refinements in voice leading were suggested depending upon whether the imperfect intervals were major or minor.118 On the other hand, movement from a perfect to an imperfect consonance was generally freer "since one can pass easily from perfection to imperfection though not the reverse."119 There is, one may note, a certain air of futility to Zarlino's instructions in these areas, for practice, as Artusi has already observed for us, permitted many exceptions.120
One looks in vain for additional instructions. Our attempts to explain the compositional process, which began with the interval, end there. The treatises are limited to explaining, first, how acceptable tonal combinations result—complete with a broad panoply of philosophical implications—and, second, how one tonal combination succeeds another. Here, often, the unwieldy philosophical apparatus is abandoned, though the implicit force of its presence is felt. Hence, we learn about acceptable melodic movement from one note to the next (though not through a series of intervals forming a melody); we learn to avoid parallel perfect intervals; we learn how to progress from one consonance to another; we learn about the collocation of consonance and dissonance; we learn how to treat the latter acceptably; etc. The result is a short-winded approach to composition which some commentators have regarded as the greatest deficiency of sixteenth-century treatises. Thus, Marco, a translator of Book III of the Istitutioni harmoniche, writes:
We find only vague directions about the choice of harmonies, the placing of cadences, voice-leading, melodic shapes, rhythmic structure and scope or form of an entire work. True, a knowledge of all these matters may be derived from their examples, but the examples are more a sampling of contemporary practice than an explanation of it, and a student seeking from general principles might find them just as quickly by consulting actual Masses and motets of good composers.
What guidance the student did receive was largely of a negative nature; by carefully stepping among the innumerable prohibitions he was expected to find a pleasing path to the final cadence.121
As for modal theory,122 its derivation from early monodic forms, and its unsettled and confusing state when applied to sixteenth-century polyphony, rendered it totally inadequate for explaining the harmonic forces with which composers dealt as a matter of course. On at least five counts the treatises proved their insufficiency, for nowhere did they take adequate cognizance of the following:
1. The binding logic of harmonic progression which in actual music, if not in theoretical writings, was at least as fundamental and compelling as melody in establishing and maintaining the mode.
2. The importance of the cadence as a point of focus and direction for harmonic motion; the overall relation of harmonic points established in cadences to one another.
3. The deviations from purely melodic laws in each voice part, particularly at cadences, in order to satisfy harmonic requirements. Occasionally one finds clues explaining such deviations in discussions of hexachord usage, the genera, and musica ficta which point to a certain awareness of the effect of these factors within the mode. However, modal theory itself failed to account for them.
4. The harmonic relationships among simultaneously sounding tones, especially in compositions of more than two parts. Oddly enough, during the sixteenth century when four-part and later five-part writing became standard, the triad (though not so-called) was defined as "the concent which is produced by at least two consonant intervals combined and united according to the grades of proportionality. . . ."123 Of course, it was for this very reason that Rameau later criticized Zarlino. "The error in Zarlino's application of his rules," suggested Rameau, "lay in his consideration of not more than two parts at one time."124
5. The particular chordal progressions, bass movements, cadential formulas, etc., characteristic of a given mode.
The most we can find in the treatises are cursory instructions for "pairing" modes, an approach which suggests that one part in the authentic mode should be counterpointed by a second in its plagal. Thus, instructs Glarean,
a Hypodorian Tenor is arranged so that its bass is Dorian. . . . When the Mixolydian is in the tenor, the cantus and bass have the system of Hypomixolydian. . . . Likewise, when the Hypoionian is arranged, the Ionian comes into the bass. Finally, if the tenor has a common fifth of two modes, these modes will be complete in the outer voices, as the authentic in the bass, the plagal in the cantus. In general, the bass voice inclines to the authentics, the cantus to the plagals, in a certain natural reason more admirable than explicable.125
There are two problems inherent in this approach. The first Glarean himself suggests, for almost as often as a Hypodorian tenor is accompanied by a Dorian bass, it is accompanied by an Aeolian. Similarly, the Mixolydian may be combined with the Dorian, the Phrygian with the Aeolian, the Ionian with the Lydian, etc.126 Obviously, the pairing of authentics and plagals was far from universally observed by composers.
The second problem in Glarean's approach is more basic to our discussion. For the examination of two parts paired according to authentic and plagal ranges is but one step removed from the examination of a single part. It can scarcely account for harmonic laws governing all parts, nor still less for the give and take which occurs between voices simultaneously combined. Nor could it have been the sole consideration which guided composers in their harmonic usage.
To some extent, additional information is provided by discussions centering on the beginning of a composition and on the cadence. Instructions regarding the former give the proper starting tones for a mode; in so doing they carry both melodic and harmonic implications. Zarlino indicates the proper pattern in his explanation of the first mode:
. . . the true and natural beginning, not only for this mode but for every other, is on the tones outlining its fifth and fourth and on the intermediate tone which divides the fifth into a major and minor third.127
Thus, in the first mode, D, F, A, and D are available. There are also other tones available, says Zarlino, but too numerous to mention. Implicit in his dismissal of these is the notion that the "true and natural" tones offer the best possibilities. In this light, we cite Morley's criticism of a student work in which "the bass is brought in out of key,"128 that is, on some tone other than those outlined by Zarlino.
The same, D, F, A, and D, also serve as the tones for the regular cadences; any others are referred to as irregular.129 Obviously, the normal starting tones and the regular tones for cadences serve as means to establish and maintain the mode. In this respect, Artusi is more explicit. He states that the composer maintains the mode primarily by beginning, ending, and having medial cadences on the regular tones of that mode. He also suggests the possibility of two irregular cadences "so that the composer will have at his disposal a broad sphere in which to operate."130 A more progressive theorist like Vicentino was somewhat bolder. He suggests that
one may use many cadences besides those on the principal tones of the mode. These may be placed in the middle of the composition, after the composer has made cadences on the principal tones. For then, between these principal tones, he may insert cadences from other modes. However, he must proceed in a good manner . . . so that when the singer approaches them, they will not seem strange to the listener. If the composer proceeds in this manner he can write any kind of cadence outside of the mode.131
He illustrates some possibilities for the first mode with the examples in Figure 12 without, however, establishing relationships among the cadential possibilities, nor assigning what we would regard as key-defining functions to them.
Fig. 12.—Cadences from outside of the mode.

The Theoretical Conception of Harmony in Music
In summary, then, we arrive at the following conclusions concerning harmony in music:
1. The basic unit of sixteenth-century harmony, regardless of the number of voices, was the consonant interval, carefully defined and absolutely predetermined by reference to higher (mathematical) orders.
2. In actual composition, dissonant intervals were to be judiciously intermingled with consonant intervals, the former being carefully placed according to well-defined procedures. It is perhaps in this area that the treatises were most explicit and consequently most useful to the aspiring composer.
3. A basic assumption, though not explicitly stated, is that in writing for three or more voices, each tone must be consonant with all others sounding simultaneously, or, if dissonant, must be treated according to the procedures established for two voices.
4. All voices should be restricted to the tones within the authentic and plagal modes sharing the same final as much as possible. Exceptions included alterations to provide a leading tone at cadences, to avoid such awkward intervals as the tritone, or in accordance with the procedures for the mutation of one hexachord to another.
5. It is best to begin and end a composition, and place most cadences on the true and natural tones of the mode (root, third, and fifth of the tonic, to use modern terminology). It is difficult to determine how much deviation from this advice was theoretically acceptable, and impossible to glean from the treatises how the overall dimensions of a composition might affect this advice.
The answer to one of the questions we posed for ourselves earlier, then, is that sixteenth-century theory offers only an incomplete doctrine for explaining musical harmony as practiced at the time. Yet the deficiency in accounting for long range harmonic forces or vertical sonorities beyond two parts may only seem to be such in the perspective which we bring to the discussion. Given the precepts for dissonance treatment, acceptable melodic intervals, modal integrity, and the broad, though vague principles of musical composition outlined by Zarlino, perhaps little else is needed beyond, let us say, a touch of musical imagination.
A RELATIONSHIP BETWEEN PHILOSOPHICAL AND
MUSICAL CONCEPTIONS OF HARMONY?
From our discussion of the compositional process, and particularly of the shortcomings of harmonic theory, it begins to appear as if music lacked any unique rational foundation based on a study of the higher orders of harmony which music purported to mirror—this, in spite of the cumbersome apparatus adopted by theorists to prove otherwise. As is all too obvious from the descriptions of intervallic combinations which passed for instruction in composition, there were no rational, mathematical, and immutable forces which governed the combination of intervals into music as there seemed to be for the combination of tones into intervals. Nor were there higher, philosophical models accounting for any other musical phenomena. Instead, the compositional process was dependent upon experience, taste, and talent; then, as now, it was a subjective affair whose chief tenets were culled from the empirical and analytical study of real music. The weight accorded the proportional bases for intervals, and the resulting philosophical projections would seem to belie this, but those portions of the treatises devoted to compositional processes substantiate it. It is as if the modern writer of a harmony text were to expend half of his energy and three-quarters of his pages on the physical laws of, let us say, the overtone series, in the belief that similar laws governed the exposition of the musical principles which followed. The best theorists of the period, no doubt, intuitively understood that such could not be the case and ultimately viewed music as the subjective art which it is—a product of its own laws created without reference to any other discipline. Of course, no one in the sixteenth century—with the possible exception of Galilei—stated it in even approximately these terms. However, even with theorists who ostensibly sought to expose a series of rational musical laws culled from higher orders of harmony, there are clues that judgment and taste took precedence where contradictions or gaps in knowledge occurred. Observe the following:
It must be noted that I do not set down particular rules concerning the ways to be followed in writing counterpoint on a subject, but only the universal. Thus, from the rules outlined above, it is necessary that the composer extract the parts of the counterpoint by means of his own intellect and judgment. For the acquisition of whatever rules and precepts is of little value if nature has not endowed him with talent.132
A statement like the above obviously precludes the possibility of immutable laws based on higher models, while the following clearly indicates the empirical approach which we suggest:
[If modern music] is purged of errors and mistakes and arranged in good order, it is because modern composers have turned to the rules of their predecessors and focused their attention upon hearing the effects made by [well] modulated cantilene.133
The subjective element
In light of the above, it seems worthwhile to digress for a moment to examine more carefully the respective roles of reason and sense, of subjectivism and rationalism, of the purely musical and the philosophical in sixteenth-century music. In so doing we hope to introduce the notion that the Renaissance theorist was in reality Janus-faced: conservative and backward looking when he attempted to present an organic whole of the philosophical and musical precepts which he felt governed his art; progressive and forward looking when he resolved contradictions between preconceived philosophical notions and his musical ear by choosing the latter. In both attitudes he was unique: if, on the one hand, his attempts to unify speculative and practical considerations were new, so too, on the other, were his efforts at weighing and evaluating the effects of actual composition. Indeed, it had not been too many years prior when a denial of the subjective element and a Boethian distrust of sense-perception had prevailed. It is instructive to compare the following from Jacques LeFebvre with the approach to a similar problem faced by Zarlino:
The semiditonus [minor third] lies between the ratios 6:5 and 7:6; although it is pleasing in sound to the ear, it is, nonetheless, not to be regarded as a consonance. . . . The fact that the minor third sounds pleasing is proved by one's experience in listening to musical compositions; it is not, however, a consonance, because its ratio (32:27) is neither super-particular nor is it a complexity which can be reduced to a simple ratio.134
As we have seen, Zarlino, in order to justify the inclusion of the minor sixth among the consonances, followed a rather dubious line of reasoning. He could, like LeFebvre, and for similar reasons, have rejected it; that he did not may be regarded as a triumph of the empirical approach—and of the subjective element—over mathematical rigidity and philosophical preconception. The fact that he later was able to resolve his inconsistency by referring to a second numero sonoro, the ottonario,135 only proves further the contention that when theory lagged behind practice, ways were found to narrow the gap.
Reason and sense
The strongest indication of the new importance attached to the subjective element in music, however, came with the balance of reason and sense maintained by most sixteenth-century theorists. No doubt, the first step in achieving such an equilibrium was the new eminence granted the senses within the total human faculty. For if the Medieval world, after Boethius, had elevated reason above sense—because "the peculiar property of sensible things is not so apparent or intelligible save by proper investigation and reflection upon the facts"136—the sixteenth century mollified such distrust by placing reason and sense on equal footing. Perhaps this reconciliation was a reflection of the Aristotelian observation, paraphrased by Zarlino, that "intelligence, or intellect, or reason (whichever you wish to call it), originates . . . in the senses." For, explained Zarlino, "nothing can exist . . . in the intellect . . . which has not first been received by the senses."137 Obviously, in such a relationship, reason and sense were rather more complementary than opposed: the former clearly depended upon the latter for external stimuli, and the latter, upon the former for interpretation.
The chief impetus for a reconciliation between reason and sense, however, came from the writings of Aristoxenus and Ptolemy, whose works Zarlino had caused to be translated into Latin around the middle of the century.138 The older of this pair, Aristoxenus, apparently served the purpose of providing a view opposite to that of Pythagoras; Ptolemy, then, functioned as a kind of intermediary between the two. For, as Zarlino explained, the Pythagoreans
left sense to one side, so to speak, in examining tones with reason; and . . . [the Aristoxenians] ignored reason and followed sense. But it was difficult, indeed, impossible, to know exactly how to measure the distance between tones of different pitches, without, on the one hand, sense, or on the other, reason (the true judges of such things). . . . Because of this, the great mathematician, Ptolemy . . . decided that it would be good if, in considering tones, one made use of sense as a beginning, but accompanied it also with reason, the former in order to comprehend well if the tones are consonant or dissonant and which of the two is higher, and the latter to learn how much one is distant from the other, or different in proportion, and how much one surpasses the other in quantity and quality.139
Still, aside from the subjective aspect which was implied in the references to sense, it is difficult to understand precisely what the new reconciliation of reason and sense meant when applied to music. It is clear enough in its application to the interval. But there, as seems evident, the term rational is almost synonymous with mathematical. And, at all events, the kind of reasoning applied to the interval could in no way be extended to actual music. It is, perhaps, unfortunate that Aristoxenus was not better understood by sixteenth-century theorists, although cited often enough.140 For one suspects that the real meaning behind the frequent invocations to reason and sense lay in the following:
It is plain that the apprehension of a melody consists in noting with both ear [sense] and intellect [reason] every distinction as it arises in the successive sounds. . . . For the apprehension of music depends on these two faculties, sense-perception and memory; for we must perceive the sound that is present, and remember that which is past. In no other way can we follow the phenomenon of music.141
And elsewhere, another reference to hearing and the intellect: "By the former we judge the magnitudes of the intervals, by the latter we contemplate the functions of the notes."142
Lippman, who quotes these and other passages, reaches the following conclusion which we borrow for its relevance to our own discussion:
The peculiarity of the method [of Aristoxenus] is that hearing and reason do not really act together; they are assigned to distinct tasks. Thus reason is responsible for the logical structure of the whole science and its particular arguments, as well as for determining the functional relationships between the tones; but it does not participate in the judgment of the size of intervals; this depends solely on auditory discrimination.143
If this is the real meaning of reason and sense, then it is clear that the sixteenth century not only lacked a rational or philosophical basis for musical composition but was deprived as well of any special confluence of the intellect and ear in musical composition. For the union suggested by Aristoxenus is universal to the musical art and, though perhaps restated by successive epochs in different terms, hardly to be regarded as the distinctive achievement of any particular period.
CONCLUSIONS
Needless to say, sixteenth-century musicians hardly viewed matters in this way. Indeed, the point is a purely academic one when considered in the light of sixteenth-century theoretical writing. What is important is the belief that reason and sense were balanced; this led to the beginnings of an empirical approach to musical analysis based on a carefully considered examination of audible phenomena; it also invested the achievements in theory and composition with an aura of irrevocable authority; hence did Zarlino become a lawgiver. What is important is the belief that the rational basis for the interval extended into music itself: this led to the notion that the analysis of music was somehow analogous to the systematic, mathematical examination of the interval; it also extended to the compositional process a rational and philosophical basis which, in fact, it did not have. What is important is the belief that the philosophical conception of harmony was somehow reflected in music: this resulted in the faith given to proportion and caused, as well, the restraint and proper relationship between parts which was implied in the word proportionate; it also called for an imitation of nature which, in turn, served to explain both the order and higher purposes to which music aspired. At the very best these beliefs served as the bases for such a monumental treatise as Zarlino's Istitutioni harmoniche and, perhaps, less directly, for the music of, let us say, Palestrina; at the worst, they led to the intransigency of, for example, an Artusi in his famous polemic with Monteverdi which began the seventeenth century.
As a final note to this article, the author has been tempted to draw a paradigm after the fashion of sixteenth-century theorists who delighted in such things. In the very center, in the smallest box possible, would be placed the word INTERVAL. At some short distance to the left would be placed the word REASON, emitting rays of knowledge to the box. At a similar distance to the right of the box would be placed the word SENSE, sending rays of perception to the box. Immediately above the box and tangent to it would be drawn a huge circle. In the center of the circle would be the inscription PHILOSOPHICAL CONCEPTION OF HARMONY. Placed at appropriate points along the circumference of the circle would be three additional inscriptions: COMPATIBLE JOINING OF DIVERSE ELEMENTS; PROPORTION; HIERARCHY OF ORDERS. Below the box and stemming from its corners would be two divergent lines. Placed between these two lines would be the words MUSICAL CONCEPTION OF HARMONY. On the divergent lines would be the appropriate inscriptions as they relate to contrapuntal practice: perhaps, SENARIO; NUMERI SONORI; CONSONANCE; DISSONANCE; MODES; etc. Unfortunately, because some of the appropriate inscriptions would be incomplete, the author has not yielded to his temptation. Missing, for lack of information in the theoretical sources, would be suitable descriptions of the proper relations between chords, and their long-range harmonic function. Thus we arrive at a final paradox: while the sixteenth-century conception of harmony held by musical theorists meant much more in a philosophical sense than our own, it meant much less in a musical one.
1Aristotle, Metaphysics 2. 1. 5-7. See Nan Cooke Carpenter, Music in the Medieval and Renaissance Universities (Norman, Oklahoma: University of Oklahoma Press, 1958), p. 26. The division was perhaps first drawn into music in the second or third century by Aristides Quintilianus. See "Aristidis Quintiliani, de musica libri III," in Antiquae musicae auctores septem. Graece et latine, ed. by Marcus Meibomius (2 vols.; Amsterdam: Ludovicum Elzevirium, 1652), II, 207. The division made by Aristides is reproduced in John Hawkins, A General History of the Science and Practice of Music [1776] (2 vols.; New York: Dover Publications, Inc., 1963), I, Book II, xiii, p. 61. See John Hollander, The Untuning of the Sky: Ideas of Music in English Poetry, 1500-1700 (Princeton, New Jersey: Princeton University Press, 1961), p. 22.
2For a discussion of the various types of treatises see Carpenter, Universities, pp. 26-31 and passim.
3Cf., for example, the writings of Pietro Aaron who produced as his contribution to speculative thought Libri tres de institutione harmonica . . . ([Bologna: B. Hector, 1516]), and, for practical purposes, Compendiolo di molti dubbi, segreti et sentenze intorno al canto fermo, et figurato . . . (Milan: Per Io. Antonio da Castelliono stampatore [ca. 1545-50]); Lucidario in musica . . . ([Venice: Girolamo Scotto, 1545]); Toscanello in musica . . . ([Venice: Bernardino e Matheo de Vitali, 1520]); or Trattato della natura et cognitione di tutti gli tuoni di canto figurato non da altrui più scritti . . . ([Venice: Bernardino de Vitali, 1525]). See also Franchino Gafori, Theorica musicae [1492] facsimile edition, prefazione a cura di Gaetano Cesari (Rome: Reale Accademia d'Italia, 1934), and Practica musicae . . . ([Venice: Augustium de Zannis de Portesio, 1502]).
4(Venice: By the author, 1558). Facsimile edition (New York: Broude Brothers, 1965).
5"Et se la Speculativa senza la Prattica (come altre volte hò detto) val poco; atteso che la Musica non consiste solamente nella Speculativa; cosi questa senza la prima è veramente imperfetta. Et questo è manifesto: conciosia che havendo voluto alcuni Theorici trattare alcune cose della Musica; per non havere havuto buona cognitione della Prattica, hanno detto mille chiachiere, & commesso mille errori. Simigliantemente alcuni, che si hanno voluto governare con la sola Prattica, senza conoscere alcuna ragione, hanno fatto nelle loro compositioni mille, & mille pazzie. . . ." Ibid., III, lxvi, p. 261. See also ibid., I, xiv, pp. 20-21.
6Among these are Domenico Pietro Cerone, El melopeo y maestro . . . (Naples: Iuan B. Gargano y Lucrecio Nucci, 1613); Marin Mersenne, Harmonie universelle . . . (Paris: S. Cramoisy, 1636); Athanasius Kircher, Musurgia universalis . . . (Vol. I, Rome: F. Carbelletti, 1650; Vol. II, Rome: Grignani, 1650).
7Zarlino among them. We read in the preface to Antonio Gogava's translation of four ancient Greek texts an acknowledgment of Zarlino's commission: "Cum pridem libros Harmonicorum Cl. Ptolemai multorum gratiam edere statuissem, submonuit me doctiss. Musicus Iosephus Zarlinus clo diensis, ut Aristoxeni quoq; eadem de re libros, paucis hactenis visos, in Latinum sermonem transferrem, & Ptolemaeo, quamvis ab illo differentienti, adiungerem." Aristoxeni musici antiquiss. Harmonicorum elementorum libri III. Cl. Ptolemaei Harmonicorum, seu de musica lib. III. Aristotelis de obiecto auditus fragmentum ex Porphyrij commentarijs. Omnia nunc primum latine conscripta & edita ab Ant. Gogavino . . . (Venice: V. Valgrisium, 1562), p. 6.
8For a full discussion of Greek conceptions of harmony, see Edward A. Lippman, Musical Thought in Ancient Greece (New York: Columbia University Press, 1964), pp. 1-44.
9Problems 19. 38; quoted in Gretchen L. Finney, "Music: a Book of Knowledge in Renaissance England," Studies in the Renaissance, VI (1959), 43, n. 38.
10De re publica 2. 42. 69; quoted in Finney, "Music: a Book of Knowledge," p. 43, n. 38.
11See, for example, Boethius, De institutione musica, ed. by Gottfried Friedlein (Leipzig: B.G. Teubner, 1867), I, ii, p. 188; trans. in Oliver Strunk, ed., Source Readings in Music History from Classical Antiquity through the Romantic Era (New York: W.W. Norton and Company, Inc., 1950), p. 84. See also the explanation of harmony as "a concordant blending of diverse sounds," in the "Scholia enchiriadis," ibid., p. 134; or the motto: Harmonia est discordia concors which appears on the woodcut frontispiece of Gafori, De harmonia musicorum instrumentorum opus (Milan: de Ponte, 1518). See also the definition of harmony given in Johann Gottfried Walther, Musikalisches Lexicon oder musikalische Bibliothek, Faksimile-Nachdruck, hrsg. Richard Schaal, Documenta Musicologica, erste Reihe, Vol. III (Kassel: Bärenreiter Verlag, 1953), p. 300.
12". . . in universale, . . . Musica non è altro che Harmonia; & potremo dire, che ella sia quella lite & amicitia, che poneva Empedocle, dalla quale voleva, che si generassero tutte le cose, cioè una discordante concordia, come sarebbe a dire, Concordia di varie cose, le quali si possino congiungere insieme." Zarlino, Istitutioni harmoniche, I, v, p. 10.
13"Dico adunque che Contrapunto è quella Concordanza, o concento, che nasce da un corpo, ilquale habbia in se diverse parti, & diverse modulationi accommodate alla cantilena, ordinate con voci distanti l'una dall'altra per intervalli comensurabili, & harmonici. . . . Si può anche dire, che'l Contrapunto sia un modo di harmonia, che contenghi in se diverse variationi de suoni, o de voci cantabili . . . , o veramente che'l sia una certa unione arteficiosa de suoni diversi, ridutta alla concordanza." Ibid., III, i, p. 147.
14". . . la Consonanza . . . è mistura di suono grave, et acuto, che perviene alle nostre orecchie soavemente, et uniformemente. . . . la Consonanza nasce, quando due suoni, che sono tra lor differenti . . . si congiungono concordevolmente in un corpo." Ibid., II, xii, p. 79.
15". . . essendo la Dissonanza contraria alla Consonanza, non sarà difficile saper quello, che ella sia: Imperoche è mistura di suono grave, & di acuto, la quale aspramente perviene alle nostre orecchie. Et nasce in tal maniera, che mentre tali suoni non si vogliono unire l'un con l'altro, per la disproportione, che si ritrova tra loro; & si sforzano di restare nella sua integrità; offendendosi l'un l'altro porgono amaro suono all'udito." Ibid., p. 80.
16". . . ogni consonanza si ritrova tra due suoni distanti per il grave, & per l'acuto; i quali fanno uno intervallo; . . . però non havendo l'Unisono alcuno di questa qualità, non lo potemo chiamare per alcun modo ne Consonanza, ne Intervallo." Ibid., III, xi, p. 157. Of course, in actual composition, such considerations had no meaning, for the unison was treated like a consonance.
17See ibid., II, xii, p. 80.
18Zarlino refers to examples of parallel unisons, octaves, and fifths which he uses to illustrate his comments.
19"Vietavano dipoi gli Antichi compositori il porre due Consonanze perfette di uno istesso genere, o specie, . . . l'una dopo l'altra . . . conciosiache molto ben sapevano, che l'Harmonia non può nascere, se non da cose tra loro diverse, discordanti, & contrarie; & non da quelle, che in ogni cosa si convengono. La onde se da tal varietà nasce l'Harmonia, sarà dibisogno, che nella Musica, non solo le parti della cantilena siano distanti l'una dall'altra per il grave, & per lo acuto: ma etiandio che le loro modulationi siano differenti ne i movimenti: & che contenghino varie consonanze, contenute da diverse proportioni. Et tanto più potremo allora giudicare che sia harmoniosa quella cantilena, quanto più si ritroverà nella compositione delle sue parti diverse distanze tra l'una, et l'altra, per il grave, & per lo acuto; diversi movimenti, & diverse proportioni. Videro forse gli Antichi che le Consonanze poste insieme in altra maniera, di quella, ch'io hò detto (ancorache fossero alle volte varie ne i loro estremi per il grave, & per lo acuto) erano simili nel procedere, & simili di forma nelle loro proportioni: però conoscendo, che tale simiglianza non generava alcuna varietà di concento, & giudicando (come era il vero) che la perfetta harmonia consistesse nella varietà . . . però non volsero, che due, o più Consonanze perfette, contenute da una istessa proportione, ascendenti insieme, o discendenti le parti, si potessero porre nelle compositioni l'una dopo l'altra, senza alcuno altro mezano intervallo." Zarlino, Istitutioni harmoniche, III, xxix, p. 176.
20Elsewhere, Zarlino refers specifically to the monochord, the instrument usually employed for such purposes. See Zarlino, Istitutioni harmoniche, II, xxvii, p. 97, or idem, Dimostratione harmoniche . . . (Venice: Per Francesco de i Franceschi Senese, 1571), p. 212.
21". . . piglia primieramente lo istrumento, nel quale si ritrova la materia preparata, cioè le chorde; dipoi per poter conseguire il desiderato fine, introducendo in esse la forma delle consonanze, le riduce in una certa qualità, & in un certo temperamento, ponendo tra loro una distanza proportionata, & tirandole di modo, che percosse da lui rendeno poi perfetto concento, & ottima harmonia." Zarlino, Istitutioni harmoniche, I, xli, p. 54.
22"Questa Consonanza è la prima di tutte l'altre. . . ." "Ma si come non si trova proportione, che sia avanti la Dupla: cosi non si trova Consonanza, che sia prima della Diapason poi che la Dupla è la sua vera forma." Zarlino, Dimostrationi harmoniche, p. 88. Dupla simply means the ratio 2:1.
23Zarlino, Istitutioni harmoniche, I, xvii-xx, pp. 28-31.
24". . . il fine dell'attione, . . . è il Sonare con harmonia; overo il giovare, & dilettare, che si dice cagion finale; lo Agente, cioè il Musico, che si nomina cagione efficiente; la Materia, che sono le chorde, & si chiama cagione materiale; & la Forma, cioè la proportione, che si addimanda cagione formale; nondimeno queste due ultime sono cagioni intrinseche della cosa; & l'Agente, & il Fine sono cagioni estrinseche: conciosia che queste non appartengono ne alla natura, ne all'esser suo; & quelli sono parti essentiali di essa: percioche ogni cosa corruttibile è composta di materia & di forma. Et la Materia si dice quella, della quale si fa la cosa, & è permanente in essa, si come i suoni de i quali si fa la Consonanza; & la Forma è quella specie, o similitudine, o vogliam dire essempio, che ritiene la cosa in se, per la quale è detta tale; si come è la proportione nella Consonanza. E questa si chiama cagione intrinseca, a differenza della estrinseca; la quale è (per dir cosi) il Modello, o vigliam dire Essempio, alla cui similitudine si fa alcuna cosa; si come è quella della Consonanza, che è la proportione di numero a numero." Ibid., I, xli, p. 54. Cf. Aristotle, Metaphysics 1. 3; Physics 2. 3. 7.
25"La proportione adunque è la causa formale . . . delle consonanze; . . . si hanno da regolare & proportionare li corpi sonori. . . ." Zarlino, Istitutioni harmoniche, I, xli, p. 55.
26". . . maestra di tutte le cantilene, . . ." Ibid., I, x, p. 20.
27". . . essendo il Numero inseparabile dalla consonanza." Ibid., I, xx, p. 31.
28Ibid., I, xxi, p. 31.
29Ibid., II, xii, p. 80.
30". . . dalla prima origine del mondo (si come manifestamente si vede, et lo affermano i Filosofi) tutte le cose create da Dio furno da lui col Numero ordinate: anzi esso Numero fu il principale essemplare nella mente di esso fattore. Onde è necessario che tutte le cose, le quali sono separatamente, overo insieme, siano dal numero comprese, & al numero sottoposte: imperoche tanto è egli necessario; che se fosse tolto via, prima si distruggerebbe il tutto, & dipoi si levarebbe all'huomo (come vuol Platone) la prudenza, & il sapere: conciosiache di niuna cosa, che egli havesse nell'intelletto, overo nella memoria, potrebbe rendere ragione; & le arti si perderebbeno, ne più faria bisogno di parlare o scrivere alcuna cosa della Musica; percioche del tutto la ragione di essa si anullarebbe, non havendo ella maggior fermezza, che quella de i numeri." Ibid., I, xii, p. 2l.
31Aristotle, Metaphysics 1. 5; trans. by Hugh Tredennick (Cambridge, Massachusetts: Harvard University Press, 1961), p. 33. If the universality of number was not stated strongly enough in Aristotle's account of its origins, there could be no doubt of its significance in the writing of Philolaus: "Consider the effects and the nature of number. . . . It is great, all-powerful and the guide in life, of Gods, of Heaven, of men. Without it all is without limit, obscure, indiscernible. The nature of number is to be a standard of reference, of guidance, and of instruction in every doubt and difficulty. Were it not for number and its nature, nothing that exists would be clear to anybody either in itself or in its relation to other things. . . . You can observe the power of number exercising itself not only in the affairs of demons and of gods, but in all the acts and thoughts of men, in all handicrafts and in music. Nor does harmony and the nature of number admit of any falsity. . . . Only to the unlimited, the unintelligible, the irrational, do falseness and envy belong." Trans. by Benjamin Farrington, Greek Science (2 vols.; Middlesex, Great Britain: Penguin Books, 1944-1949), I, 42.
32". . . conciosia che la forma sia più nobile della materia." Zarlino, Istitutioni harmoniche, I, xx, p. 31. In his application of Aristotle's "four causes," Zarlino was quoted earlier in our paper as having written that "the proportion of number to number is the model for consonance." See p. 14.
33Roger Bacon, Opus majus, trans. by R.B. Burke (2 vols; Philadelphia: University of Pennsylvania Press, 1928), I, 198.
34Cf. Boethius, De institutione musica, trans. in Strunk, Source Readings, pp. 84-85. See also Albert Seay, Music in the Medieval World (Englewood Cliffs, New Jersey: Prentice-Hall, Inc., 1965), pp. 20-22.
35Trans. by D.P. Walker, "Ficino's Spiritus and Music," Annales Musicologiques, I (1953), 143-144.
36Walker points out that certain of Ficino's ideas did not seem to have much influence on subsequent theorists; ibid., pp. 148-149.
37See the dedication to Johannes Tinctoris, The Art of Counterpoint, trans. and ed. with an introduction by Albert Seay ([Rome]: American Institute of Musicology, 1961), p. 14. The dedication is also translated in Strunk, Source Readings, pp. 197-199.
38. . . gli orecchi nostri non possono capire la dolcezza dell harmonia celeste, per l'eccellenza et grandezza sua." Zarlino, Istitutioni harmoniche, I, vi, p. 12. At the end of the next chapter on musica humana, Zarlino confesses with apparent relief that "these things pertain more to discussions of philosophy than to music. . . . Since it adds little or nothing to our subject, we will make no further mention of it." (". . . questa cose s'appartengono più alli ragionamenti della Filosofia, che a quelli della Musica . . . della quale, come di quella, che nulla o poco fa al nostro proposito, non ne farò più mentione.") Zarlino, Istitutione harmoniche, I, vii, p. 18.
39See Harold S. Wilson, "Some Meanings of 'Nature' in Renaissance Literary Theory," Journal of the History of Ideas, II (1941), 430-448. See also Arthur O. Lovejoy, "'Nature' as Aesthetic Norm," Modern Language Notes, XLII (1927), 444-450. See also Armen Carapetyan, "The Concept of Imitazione della natura in the Sixteenth Century," Journal of Renaissance and Baroque Music, I (1946), 47-67.
40Cf. Leo Schrade, "Von der Maniera der Komposition des 16. Jahrhunderts," Zeitschrift für Musikwissenschaft, XVI (1934), 14.
41"Mentre che gli Antichi Filosofi acutissimi, & sottilissimi investigatori, et inventori delle cose, andorno considerando gli effetti, che nel Mondo superiore, et nello inferiore dalla Madre natura vengono prodotti; conobbero che de' Cieli il moto loro non era uno dall'altro, nè usurpato, nè impedito; ma inviolabilmente osservato: che il Sole faceva egualmente il suo corso, senza mai fermarsi; che la Luna similmente con egual ordine procedeva; che il giorno non si tramuttava nella notte, nè la notte ne'l giorno; che gli animali volatili osservavano di stare nella sua Regione dell'aria non entrando ne' luochi de' pesci; che il pesce non usciva de' suoi confini; che gli alberi distintamente uno non produceva il frutto dell'altro, ma ognuno secondo la sua specie faceva quello che dalla natura gli era stato preordinato; che le viti non facevano pomi, nè peri; nè le Quercie producevano uva; & che la terra osservava il modo di produrre l'herbe verdi. Per laqual cosa maravigliati di cosi fatto ordine, per ilquale si distinguono le cose l'una dall'altra diferentemente dalla perniciosa confusione. . . ." Giovanni Maria Artusi, "Prima consideratione," Seconda parte dell'Artusi, overo della moderna musica . . . (Venice: Giacomo Vincenti, 1603), p. 1.
42". . . l'arte deve imitare la natura quanto puo nelle sue operationi; . . . è necessario, che habbino una certa proportione, ò temperatura, altrimente da' nostri sensi sarieno sprezzate, & abhorrite. . . ." Giovanni Maria Artusi, L'arte del contraponto . . . nella quale con ordine, e modo facilissimo si insegnano tutte quelle regole che à questa arte sono necessarie. Nuovamente ristampata, & di molte nuove aggiunte dall'autore arrichita (Venice: Giacomo Vincenti, 1598), p. 78.
43Diminished counterpoint involves small and varied note values, dissonances, and generally independent rhythms between voice parts; it is a term used to differentiate the normal manner of composition from "the counterpoint of note against note" which is "necessary to all beginners so that they may practice the placement and distances between consonances" (è necessario a tutti li Principianti, per far la prattica di conoscere il Sito, & le Distanze delle Consonanze . . . ). Zarlino, Istitutioni harmoniche, III, xlii, p. 195.
44"Lasciorno i nostri per Regola Universale, che si come ne' Contraponti diminuti le Consonance fossero paste ne' luochi, à loro dalla natura constituiti, la quale pose ordine, non solo alle cose animate, ma alle inanimate ancora; . . . in questa modo si procedeva con la più vicina, cosi dalla natura determinato; & come io, nell'Arte del Contraponto hò dimostrato. Cosi, & non altrimenti, nell'uso delle Dissonanze, si deve procedere, cioè, che dietro alla Dissonanza, gli seguiti quello Intervallo, che la natura, gl'ha dato il luoco, & determinato; & sarà là più à lei vicina. . . ." Giovanni Maria Artusi, Seconda parte dell'arte del contraponto nella quale si tratta dell'utile & uso delle dissonanze . . . (Venice: Giacomo Vincenti, 1589), II, ii, p. 28.
45For consonant intervals, the octave follows the major sixth, the fifth follows both the minor sixth and the major third, the unison follows the minor third. For dissonant intervals, the third succeeds both the second and the fourth, and the sixth succeeds the seventh. Ibid.
46". . . la qual regola à mio giudicio non pare, che universalmente sia vera, ma che patischi eccettioni assai. . . ." Ibid.
47Wilson, "Some Meanings of 'Nature'," p. 439.
48"Questa [i.e., music] eccita l'animo, muove gli affetti, mitiga & accheta la furia, fa passare il tempo virtuosamente, & hà possanza di generare in noi un'habito di buoni costumi; massimamente quando con li debiti modi & temperatamente è usata. . . ." Zarlino, Istitutioni harmoniche, I, iv, p. 9.
49". . . con la Musica, si lauda et ringratia il Creatore." Ibid., I, ii, p. 6.
50". . . la Musica veramente, oltra che rallegra l'animo, riduce anche l'huomo alla contemplatione delle cose celesti. . . ." Ibid.
51". . . si potrebbe dire, colui non essere composto con harmonia, il quale non piglia diletto della Musica. . . ." Ibid., I, iv, p. 9.
52"La onde potemo dire che quelle istesse proportioni, che si ritrovano nella cagione dell'Ira, o del Timore, o di altra passione nelle sopradette qualità; quelle istesse si ritrovino anco nelle Harmonie, che sono cagioni di concitare simili effetti." Ibid., II, viii, p. 73.
53". . . conciosia che la Similitudine (come vuole Boetio) ad ogn'uno è amica, et la Diversità contraria & odiosa: Ma se aviene, che ne oda una di proportione diversa, tal passione diminuisce, & se ne genera una contraria: Et si dice, che allora tale harmonia purifica da tal passione colui, che la ode, per la corruttione, et per la generatione di un'altra cosa contraria; come si vede, che se alcuno è molestato da alcuna passione, la qual venga con tristezza, o con lo accendersi il sangue, come la Ira; & oda un'harmonia di contraria proportione, la quale contenga alcuna dilettatione, allora cessa in lui l'Ira, & si corrompe; & immediatamente si genera la mansuetudine: cosa che suole avenire anco nell'altre passioni: Percioche ogn'uno naturalmente si diletta più di quella harmonia, la quale è più simile, conveniente, & proportionata alla sua natura et complessione, et secondo che è disposto; che di quella, che gli è contraria." Ibid., II, viii, p. 74.
54". . . il simile operava nel simile. Ha mai veduto accordare due corde unisone, overo in ottava; & che sopra una di loro vi sia posto, ò carta, ò paglia; toccata, et percossa quella sopra la quale non è cosa alcuna; la paglia ò carta posta sopra l'altra per la similitudine, et per quella simbolettà che hanno quei suoni fra di loro, se ne fugga? non farà questo effetto un'altra corda che sia d'altro temperamento; di onde s'argomenta, che il simile opera nel simile, & la cosa naturale nella natura. . . ." Artusi, Seconda parte delle imperfettioni, pp. 30-31.
55Cf. the following: "There is no doubt that the speculation of every musical composition, whether vocal or instrumental, and all that pertains to the art and science of music may be reduced to two headings. These, according to Aristoxenus, are, first, the sense of hearing and, second, the intelligence. . . . With the first we judge the size of intervals and with the second, we contemplate their faculty." (". . . però non è da dubitare, che la Speculatione d' ogni Compositione musicale, che si fà ò con le Voci, ò con i Suoni de gli Istrumenti arteficiali, & tutto'l negocio di questa Arte & Scientia, si riduca sotto due capi; de i quali come vuole Aristosseno, il primo è l'Udito & l'altro la Intelligentia. . . . Co'l primo giudichiamo le Grandezze de gli Intervalli; & co'l secondo contempliamo le loro facoltà. . . .") Zarlino, Sopplimenti musicali . . . (Venice: Appresso Francesco de' Franceschi, Sanese, 1588), I, xiii, pp. 36-37.
56From the Latin, meaning "consisting of six." However, the senario, as the discussion below will reveal, was a broader concept than mere "sixness."
57That is, six may be divided without any remainders by one, two, and three which become, by definition, its aliquot parts. Stated in another way, six is perfect because 1 × 2 × 3 = 6 and 1 + 2 + 3 = 6. Zarlino, Istitutioni harmoniche, I, xiii, p. 23. See Vincent Foster Hopper, Medieval Number Symbolism: Its Sources, Meanings, and Influences on Thought and Expression (New York: Columbia University Press, 1938), p. 44.
58The full list, of which this is only a part, may be seen in Zarlino, Istitutioni harmoniche, I, xiii, pp. 23-24.
59These terms adapted from Boethius, De institutione musica, V, x-xi, describe varying degrees of the consonant effect. Thus unisone refers to the effect of the unison, equisone to the octave, consone to the fifth and fourth, emmele to the (melodic) second, and dissone and ecmele to dissonant intervals, the latter harsher than the former. No mention is made of thirds or sixths. See Zarlino, Istitutioni harmoniche, III, iv, p. 151.
60See ibid., III, xi, p. 157.
61"Sei sono le specie delle voci musicale, tra le quali è contenuto ogni concento musicale, cioè Unisone, Equisone, Consone, Emmele, Dissone, & Ecmele. Sono dipoi sei quelle, che i Prattici addimadano consonanze, cioè cinque semplici & elementali, che sono . . . la Diapason, la Diapente, la Diatessaron, il Ditono, il Semiditono, & uno principio di esse, il quale chiamano Unisono: ancora che questo si nomini Consonanza impropriamente. . . . Oltra di questo si ritrovavano appresso gli antichi Musici sei specie di harmonia poste in uso, cioè la Doria, la Frigia, la Lidia, la Mistalidia, o Lochrense, la Eolia, & la Iastia, overo Ionica: & appresso gli moderni sei Modi principali nella Musica detti Autentici, & sei non principali detti Plagali." Zarlino, Istitutioni harmoniche, I, xiv, p. 24.
62". . . numero Senario . . . contiene in se parti, che sono proportionata tra loro in tal modo; che pigliandone due qual si voglino, hanno tal relatione, che ne danno la ragione, o forma di una delle proportioni delle musicali consonanze. . . ." Ibid., III, xv, p. 25.
63The facsimile in Figure 1 is taken from ibid.
64The facsimile in Figure 3 is taken from ibid., p. 26. The reference to large and small tones and semitones is the result of the fact that there was no universally accepted equal temperament at this time. Theoretically, "the tone can never be divided exactly in half as experience has demonstrated, for no proportion . . . can be [mathematically] divided into two equal parts." (". . . il Tuono non è mai diminuto, over fatto imperfetto della sua meza parte intera; come la esperienza lo dimostra: essendo che niuna proportione. . . . si possa dividere in due parti equali.") Ibid., III, xix, p. 165. Hence, the distinction between the large and small tones based, respectively, on the proportions 9:8 and 10:9, and between the large and small semitones based, respectively, on 16:15 and 25:14. Interestingly enough, Zarlino implies that the distinction between the respective sizes of these intervals was a matter largely for theorists and ignored by practitioners: "We have in the diatonic genus two species of tone, the large tone and the small. Thus when we find two parts in counterpoint which are separated by one of these intervals we may say that they are distant from one another by a large or small tone, or we may say that they are separated by a major second, for so the practitioners name such an interval to differentiate it from the minor second. . . ." ("Havemo adunque nel genere Diatonico due specie di Tuono, cioè il Tuono maggiore, & il minore: però quando noi ritrovaremo due parti nelli contrapunti, che saranno distanti l'una dall'altra per uno di questi intervalli, diremo, che quelle sono lontane per un Tuono maggiore, over minore; overamente diremo, che siano distanti per una Seconda maggiore: conciosia che cosi è nominato da i Prattici tale intervallo, a differenza della minore. . . .") Ibid., III, xviii. p. 164.
65"Queste sono adunque le proprietà del numero Senario, & delle sue parti, le quali è impossibile di poter ritrovare in altro numero, che sia di esso minore, o maggiore." Ibid., I, xv, p. 26. With the additional use of the ottonario at a later point, Zarlino contradicts himself. See p. 29.
66". . . percioche, come colui, che d'ogni scienza era perfetto maestro, conoscendo per opera del Spirito divino l'harmonia, che in tal numero era rinchiusa; & che dalle cose visibili & apparenti consoscemo le invisibili d'Iddio; . . . volse col mezo di tal numero in un tratto esprimere & insieme mostrare la perfettione dell'opera, & in essa la rinchiusa harmonia. . . ." Zarlino, Istitutioni harmoniche, I, xiii, p. 23.
67Ibid.
68". . . è il Principio dal quale nascono le consonanze, & senza lui ogn'altro intervallo non haverebbe il suo essere. . . ." Ibid., III, xi, p. 157.
69Ibid., I, xvi, p. 27.
70"L'Essachordo maggiore & anco il minore, nascono dalla congiuntione della Diatessaron col Ditono, o Semiditono. . . ." Ibid., I, xiii, p. 23. The ratio for the major sixth (6:5), of course, was contained in the senario, but Zarlino logically preferred to consider the two qualities of sixth as a pair. The double octave comes from the addition of two octaves; the twelfth, by the addition of the octave and fifth, etc.
71"Et benche essa tra le parti del Senario non si trovi in atto, si trova nondimeno in potenza. . . ." Zarlino, Istitutione harmoniche, I, xvi, p. 27.
72See p. 49.
73Zarlino, Dimostratione harmoniche, pp. 85-86 [misnumbered p. 74].
74Ibid., p. 94. Actually two different size tones result from this subtraction.
75Ibid., p. 95.
76Zarlino, Istitutioni harmoniche, III, xxii-xxiii, pp. 166-168.
77Ibid., III, xiv, pp. 168-170.
78Actually, Zarlino was troubled by the nature of the fourth. Disturbed by the fact that practical musicians regarded it as a dissonance (Ibid., III, v, p. 152), he is at considerable pains to prove it consonant because of its inclusion among the numeri sonori of the senario. In so doing, however, he fails to grant formal recognition to the ambivalent nature of the fourth, according to which the interval is either consonant or dissonant depending upon the musical context. He tacitly corrects this error by banishing the fourth from two-part writing unless used as a dissonance (Ibid., III, lx, p. 245), and by otherwise treating it as a consonance or dissonance in his musical examples, depending upon context. Artusi later resolves this inconsistency by including the fourth in both categories (See Artusi, L'arte del contraponto ridotta in tavole . . . [Venice: G. Vincenzi & R. Amadino, 1586], p. 9, and idem, Seconda parte dell'arte de contraponto, p. 8).
79". . . quelle consonanze . . . sono terminate da quel giorno in qua, che si incominciorno ad unire questi parti insieme nella modulatione, che sono tanti anni. . . ." Artusi, Seconda parte delle imperfettioni, p. 25.
80Artusi, L'Artusi, overo delle imperfettioni della moderna musica . . . (Venice: Giacomo Vincenti, 1600), fol. 42v; trans. in Strunk, Source Readings, p. 400. See also Artusi, Seconda parte delle imperfettioni, p. 8.
81According to Palisca, Galilei's "consonances were the octave, thirds, fifth, and sixths . . . ; the dissonances were the seconds and sevenths. The fourth, augmented fourth, and diminished fifth he placed in an intermediate category, because they sounded less harsh to the ear and were subject to fewer restrictions than the other dissonant intervals." Claude V. Palisca, "Vincenzo Galilei's Counterpoint Treatise: a Code for the Seconda Pratica," Journal of the American Musicological Society, IX (1956), 86.
82Giulio Cesare Monteverdi, "Dichiaratione della lettera stampata nel quinto libro de suoi madrigali," facsimile reprint in Claudio Monteverdi, Tutte le opere, ed. by G. Francesco Malipiero (16 vols.; Asola: Vittoriale degli Italiani, 1926-1942), X: Canzonette e scherzi musicali [p. 71]. This translation from Strunk, Source Readings, p. 410.
83". . . ogni Compositione, & ogni Contrapunto: & per dirlo in una sola parola, ogni Harmonia, si componghi di Consonanze principalmente; nondimeno per più sua bellezza, & leggiadria, si usano anco secondariamente in essa, per accidente le Dissonanze, lequale quantunque poste sole all'udito non siano molto grate; nondimeno quando saranno collocate nel modo, che regolarmente debbeno essere, & secondo li precetti, che dimostraremo; l'Udito talmente le sopporta, che non solo non l'offendeno: ma li danno grande piacere, & diletto. Di esse il Musico ne cava due utilità, oltra le altre che sono molte, di non poco valore: La Prima è . . . che con l'aiuto loro si può passare da una consonanza all'altra: La Seconda è, che la Dissonanza fa parere la Consonanza, la quale immediatamente le segue, più dilettevole; & con maggior piacere dall'udito è compresa, & conosciuta; si come dopo le tenebre è più grata, & dilettevole alla vista la luce; & il dolce dopo l'amaro è più gustevole, & più soave. Proviamo per esperianza ogni giorno ne i suoni, che se per alquanto di tempo, l'udito è offeso da alcuna dissonanza, la consonanza che segue dopo se li fa più soave, & più dilettevole. La onde gli Antichi Musici giudicarono, che nelle compositioni havessero luogo non solo le Consonanze, che chiamano Perfette, & quelle che nominano Imperfette; ma le Dissonanze ancora: percioche conobbero, che con più bellezza, & leggiadria, potevano riuscire, di quello, che haverebbeno fatto, non le havendo: Conciosiache se fussero composte di consonanze solamente, con tutto che facessero bello udire, & da loro ne uscissero buoni effetti, haverebbeno tuttavia tali compositioni (non essendo mescolate le Consonanze con le Dissonanze) quasi dello imperfetto, . . . perche mancarebbero di una grande leggiadria, che nasce da queste cose." Zarlino, Istitutioni harmoniche, III, xxvii, pp. 72-173.
84Artusi, Seconda parte dell'arte del contraponto, p. 5.
85This summary is adapted from Knud Jeppesen, The Style of Palestrina and the Dissonance [trans. by Margaret Hamerik with linguistic alterations and additions by Annie I. Fausbøll] (2nd ed. rev. and enl.; Copenhagen: Ejnar Munksgaard, 1946), pp. 94-294. Jeppesen also proposed a third category, dissonance as a means of poetical expression, which became important with the transition of the Renaissance into the Baroque.
86"Et benche io habbia detto, che nelle compositioni si usino principalmente le Consonanze, & dipoi per accidente le Dissonanze; non si debbe per questo intendere, che si habbiano a porre ne i Contrapunti, o Compositioni, come vengono fatte, senza alcuna regola, & senza alcuno ordine: percioche ne seguirebbe confusione: ma si de avertire di porle con ordine, & con regola; . . ." Zarlino, Istitutioni harmoniche, III, xxvii, p. 173.
87Zarlino informs us that the battuta provided a signal (an upward and downward hand movement) for the members of an ensemble to guide the utterance of their voices within a measurement of fast or slow time. See ibid., III, viii, p. 207. He also likens the battuta to the expansion and contraction or the rising and falling of the pulse. Ibid.
88Ibid., III, xlviii, pp. 208-209.
89". . . il Contrapuntista porre scambievolmente due minime, delle quali l'una sia consonante, & l'altra dissonante; pur che la consonante caschi nel battere, & la dissonante nel levar la battuta: ma debbeno procedere verso il grave, overo verso l'acuto per molti gradi continovati senza alcun movemento separato." Ibid., III, xlii, p. 195. Actually, though permissible, Zarlino discourages the use of dissonant half notes, "for these two parts of a whole note are strongly felt by the ear because of the battuta. . . . (". . . percioche queste due parti della Semibreve sono considerate grandemente dal senso; per rispetto della Battuta. . . .") Ibid.
90". . . quelle Semiminime, che cascano sopra'l battere, et sopra il levare della Battuta, siano accompagnate con la consonanza. Per il che sarà dibisogno, che la Prima, & la Terza semiminima si ponghino consonanti; le altre poi (si come è la Seconda, & la Quarta) non è necessario. . . ." Ibid., III, xlii, p. 195.
91Cf., for example, Zacconi, who writes: "Quarter notes, as short note values, carry with them this universal rule: beginning with a 'good' [consonant] one, we alternate a 'good' one with a 'bad' [dissonant] one. Thus, whether ascending or descending, we should always employ an even number of quarter notes, two, four, six, etc., so that the point where the progression ceases will always be good [consonant]." (". . . le Semiminime come figure veloci portano seco questa regola universale, che cominciando in buona, si mette una buona & una cattiva (andando seguente una dopo l'altra): e perche dovendo esser due, quattro, sei, e più anco sempre con parità di numero, per questo s'averte, che la positione dove vanno à finire sia sempre buona, ò sia ascendente overo descendente.") Ludovico Zacconi, Prattica di musica seconda parte . . . (Venice: Alessandro Vincenti, 1622), II, xix, p. 80.
92Artusi, Seconda parte dell'arte del contraponto, p. 45. The examples in Figure 6 should not be considered as equivalent to measures in  time. Indeed, they are not called measures by the theorist but caselle, or little boxes; each contains the equivalent of two battute.
time. Indeed, they are not called measures by the theorist but caselle, or little boxes; each contains the equivalent of two battute.
93Zacconi, Prattica di musica seconda parte, II, xlv, p. 93. Such notes are of value primarily to singers and players to embellish (per fiorire) and adorn (per abellir) the music and the harmony. By the composer they are not used except to embellish, to avoid awkward situations, and to satisfy other obligations. Zacconi also offers the following practical advice for their usage: "Many times, to the composer such figures seem easy not because in themselves they are easy, but because he was their inventor and wrote them down; to others, however, they are nothing if not awkward and difficult to perform." (". . . molte volte, al Compositore paiano facili, non perche siano facili per se, ma perche vi hà fatto prattica, e lui n'è stata l'inventore. Che ad altri poi sono più che difficultosi e difficili.") Ibid.
94"Quando . . . seguiranno due Semiminime, poste l'una dopo l'altra al modo detto di sopra, porremo sempre la seconda, che sia consonante; ancora che la prima sia dissonante: . . ." Zarlino, Istitutioni harmoniche, III, xlii, p. 199.
95Ibid.
96Zarlino, Istitutioni harmoniche, III, lxii, p. 255. Zarlino's original example is much longer and in three parts. However, at the point where the dissonances occur, the third voice has rests. The example is taken from Zarlino's chapter on double counterpoint.
97Cf. Knud Jeppesen, Counterpoint; the Polyphonic Vocal Style of the Sixteenth Century, trans. with an introduction by Glen Haydon (New York: Prentice-Hall, Inc., 1939), p. 32.
98Et tutto questo ch'io hò detto, si debbe intendere, quando la parte del Contrapunto procede per Movimenti congiunti: percioche procedendo per Movimenti separati, è necessario, che quelle figure, che contengono tali movimenti siano consonanti con la parte del Soggetto." Zarlino, Istitutioni harmoniche, III, xlii, p. 195. The word "subject" does not necessarily imply a cantus firmus but refers to the part written or conceived first. Cf. ibid., III, xliii, p. 200.
99"Conciosia che se bene la Dissonanza è posta nella seconda minima, nel movimento congiunto; tal movimento, & quel poco di velocità, che si ritrova nel proferir simili figure, non lassano udire cosa alcuna, che dispiacia. Ma non è gia cosi nelli Movimenti separati: percioche per tal separatione la Dissonanza si fa tanto manifesto; che apena si può tolerare; . . ." Ibid., III, i, p. 196.
100"Si potrà nondimeno porre la Prima parte della battuta, che sia dissonante; quando sarà la seconda minima di una Semibreve sincopata del Contrapunto; percioche la prima parte di tal figura, sarà posta senza dubbio nel levar la battuta, & seconda nel battere; & tal Dissonanza si potrà sopportare: percioche nel cantare la Semibreve sincopata, si tien salda la voce, & si ode quasi una sospensione, o taciturnità, che si trova nel mezo della percussione, dalla quale nascono i suoni, & per essa si discerneno l'un dall'altro, & consiste nel tempo; onde l'Udito quasi non la sente: percioche da lei non è mosso, di maniera, che la possa comprendere pienamente: per non esser da lei percosso, & per la debolezza del movimento, che si scorge in essa: perche manca della percussione, che lo muove: la onde la Voce allora nel perseverare della Sincopa perde quella vivacità, che havea nella prima percussione; di modo che fatta debole, et essendo percossa sopra la seconda parte della sincopa, nella quale è nascosta la Dissonanza, da un movimento più gagliardo di un'altra voce forte, che si muove da un luogo all'altro con più gagliardo movimento, tal Dissonanza a pena si ode; essendo anco, che prestamente se ne passa. Et se pure il Senso è da qualche parte offeso; è dipoi ragguagliato per tal maniera dalla Consonanza, che succede senza alcun mezo; che non solamente tal Dissonanza non li dispiace; ma grandemente in lei si compiace: perche con maggior dolcezza, & maggior soavità li fà udire tal Consonanza. Et questo forse aviene, perche Ogni contrario maggiormente si scopre, & si fà al sentimento più noto, per la comparatione del suo Opposto." Ibid., p. 197.
101Cf. Jeppesen, The Style of Palestrina, p. 227.
102". . . la Cadenza senza la Dissonanza non ha gratia, ò leggiadria alcuna. . . ." Orazio Tigrini, Il compendio della musica (Venice: Ricciardo Amadino, 1588), III, xxv, p. 78. Cf. also Zarlino, Istitutioni harmoniche, III, lxi, p. 250.
103Cf. Zarlino: ". . . because cadential formations are almost infinite, it is essential that the contrapuntist always strive to find new ones. . . ." (". . . conciosia che sono quasi infinite; onde è dibisogna, che'l Contrapuntista s'ingegni di ritrovarne sempre di nuove. . . .") Ibid., III, liii, p. 224.
104Artusi, Seconda parte dell'arte del contraponto, p. 44.
105Ibid.
106"Cercarà adunque il Compositore di fare, che le parti della sua cantilena si passino cantar bene, & agevolmente; & che procedino con belli, leggiadri, & eleganti Movimenti; accioche gli auditori prendino diletto di tal modulationi, & non siano da veruna parte offesi." Zarlino, Istitutioni harmoniche, III, xlv, p. 204. As is obvious from the context, the term modulatione did not mean changing to a new key during the sixteenth century as it does today. Instead, it referred to "a movement made from one tone to another by means of diverse intervals. It is found in every type of harmony and every type of melody. . . ." (". . . la Modulatione è un movimento fatto da un suono all'altro per diversi intervalli, il quale si ritrova in ogni sorte di Harmoni, & di Melodia; . . .") Ibid, II, xiv, p. 81. Thus, the term refers to the process of moving from note to note; a "good modulation" is merely an effective succession of such moves, avoiding, of course, prohibited intervals. It is obvious, of course, that modulation is virtually synonymous with melody except that the orientation of the latter term is toward the shape or total aggregate effect of a sequence of tones, that of the former, towards the leaps and steps connecting those tones. Explains Zarlino, "one understands the modulation of intervals to be the silent passage from one tone to another. It is intelligible, but it cannot be heard." (". . . l'Intervallo, nella modulatione, si piglia per il tacito passaggio, che si fa da un suono, o voce all'altro; il quale è intelligibile, quantunque non si possa udire.") Ibid., III, i, p. 148. In contrapuntal music, modulation also acquired the added significance implied in the process we call voice leading whereby the single tone is related not only to its immediate predecessors and successors in the melodic line, but also to whatever tones may occur simultaneously in other parts. Of course, with the notion of modulation involving, as it did, movement between tones, it is obvious that even the concept of melody was approached through intervals.
107Zarlino, Istitutioni harmoniche, III, xlv, p. 204.
108Cf. Jeppeson, The Style of Palestrina, pp. 52-55 et passim.
109". . . si come sono quelli di Decima ancora, che sarà fatto senza errore alcuno, poi che il maestro de i Musici antichi Iosquino, non pure hà usato un tale intervallo; ma etiando usò quello di Duodecima. . . ." Zarlino, Istitutioni harmoniche, III, xlv, p. 203.
110". . . alle volte si pone quello di Settima, & di Nona; ancora che di raro, si come hanno usato, & usano anco alcuni buoni Compositori." Ibid.
111Artusi, L'arte del contraponto . . . nella quale con ordine, e modo facilissimo si insegnano tutte quelle que à questa arte sono necessarie (Venice: Giacomo Vincenti, 1598), p. 38. See also idem, Seconda parte delle imperfettioni, p. 49. Artusi wrote a trio of counterpoint manuals, of which the one cited in this footnote is a compilation, revised and enlarged, of the two earlier ones mentioned in nn. 78 and 44.
112Artusi, L'arte del contraponto [1586], p. 22; idem, Seconda parte delle imperfettioni, p. 49.
113Zarlino, Istitutioni harmoniche, III, xxxiii, p. 183.
114Ibid., III, xxiv, p. 183.
115Ibid., III, xxxv, pp. 183-184.
116Ibid., III, xxxvi, pp. 184-187.
117Ibid., III, xxxviii, p. 187.
118Thus, it is best that the major sixth go to the octave, the minor sixth to the fifth, the major third to the fifth, and the minor third to the unison. If a third is to go to an octave, the third should be major, etc. Ibid., III, xxxviii, p. 188.
119"La onde ciascuna cosa facilmente (come ad ogn' uno è manifesto) dalla perfettione può passare all imperfettione; ma non per il contrario: . . ." Ibid., III, xxxviii, p. 188.
120See above, in the section The imitation of nature.
121Guy Marco, "Zarlino on Counterpoint: An Indexed Annotated Translation of the Istitutioni harmoniche, Book III; with a Glossary and Commentary" (unpublished Ph.D. dissertation, University of Chicago, 1956), p. 426.
122The present author is currently completing an article on "Modal Theory in the Sixteenth Century."
123". . . il concento che nasca da due consonanze almeno poste insieme, unite secondo i gradi della proportionalità. . . ." Artusi, L'arte del contraponto [1586], p. 7. Proportionality is a word which refers to the relation of three or more terms to one another, as in 10:9:8, while proportion, during the sixteenth century, was reserved for the relation between two terms, as in 10:9.
124"L'erreur de l'application de Zarlin ne provient que de ce au'il n'envisageoit que deux Parties à la fois dans l'établissement de ses regles & cela se trouve presque par tout . . ." Jean-Philippe Rameau, Complete Theoretical Works, Vol. I: Traite de l'harmonie réduite à ses principes naturels [1722], ed. by Erwin R. Jacobi (facsimile of Rameau's personal copy with autograph annotations; [Rome]: American Institute of Musicology, 1967), p. 89.
125Heinrich Glarean, Dodecachordon [1547], translation transcription and commentary by Clement A. Miller (2 vols.; [n.p.]: American Institute of Musicology, 1965), III, xiii, p. 250.
126Ibid., pp. 250-251. Miller concludes in his commentary that the majority of pieces cited by Glarean do show "the relation of an authentic mode to its own plagal and not to a different mode." Ibid., p. 22. However, an indication of the artificiality of Glarean's approach is attested by the theorist's need to commission a work from Gregory Meyer, a Swiss organist and friend, in order to have an example in his treatise pairing the Aeolian and Hypoaeolian modes, since he could find none in practice. Cf. ibid., III, xxiv, p. 268. See also Clement A. Miller, "The Dodecachordon: Its Origins and Influence on Renaissance Musical Thought," Musica Disciplina, XV (1961), 160-161.
127"Et benche li veri, & naturali Principij non solo di questo, ma anche d'ogn'altro Modo, siano nelle chorde estreme della loro Diapente, & della Diatessaron; & nella chorda mezana, che divide la Diapente in un Ditono, & in un Semiditono; . . ." Zarlino, Istitutioni harmoniche, IV, xviii, p. 320. At a later point in his writings Zarlino revises the numbering of the modes so that the first mode is built on C. This change can be seen in the corresponding section of the third edition of the Istitutioni harmoniche (Venice: Appresso Francesco de i Franceschi Senese, 1573), and in the Dimostrationi harmoniche, pp. 275-277.
128"Thomas Morley, A Plain and Easy Introduction to Practical Music, ed. by R. Alec Harmon (New York: W.W. Norton & Company, [1952]), p. 261.
129Zarlino, Istitutioni harmoniche, IV, xviii, p. 320. Earlier, Aaron had been more explicit, although in his listing of tones suitable for regular and irregular cadences, it turned out that any note within the mode could serve for a cadence. See Pietro Aaron, Trattato della natura et cognitione di tutti gli tuoni de canto figurato . . . ([Venice: Bernardino de Vitali, 1525]), ix-x.
130". . . potrassi pur in alcuni luochi usarne almeno due altre che siano Irregolari; & cosi il Compositore havrà il campo largo da poter discorrere à suo beneplacito." Artusi, Delle imperfettioni, fol. 68r.
131". . . s'usano molte cadentie fuori de i loro termini principali, lequali si compongano nel mezzo del procedere delle compositioni, in essempio. Quando il Compositore havrà dato i termini principali delle cadentie alle compositioni, allhora quello potrà fra quei termini comporre altre cadentie d'altri toni, ma con bel modo procederà . . . quando il cantante s'accosterà à quella, che la non paia strano all'oditore, et se'l Compositore procederà in questo ordine, egli potrà comporre ogni sorte di cadentie fuori di ogni sorte de toni." Don Nicola Vicentino, L'antica musica ridotta alla moderna prattica, Documenta Musicologica: Erste Reihe, Vol. XVII; Faksimile-Neudruck hrsg. von Edward E. Lowinsky (Kassel: Bärenreiter, 1959), III, xxii, fol. 55r.
132"Ma si debbe avertire, ch'io non pongo qui Regola particolare, del modo che si hà da tenere, nel far la parte del Contrapunto sopra un Soggetto: ma solamente la pongo universale; onde da quelle Regole, che sono poste di sopra, è dibisogno, che'l Compositore colsuo intelletto cavi la parte del Contrapunto, operando con giuditio, allo acquisto del quale vagliono poco le Regole, & li Precetti, quando dalla natura non è uno aiutato." Zarlino, Istitutioni harmoniche, III, xl, p. 192.
133". . . sono da gli errori, e sporcitie molto più ben purgati, & con più bel ordine disposti, per esser stato i moderni con le regole de Vecchi con grandissima diligenza, & fissa attentione ad ascoltare che effetto faccino le modulate cantilene. . . ." Lodovico Zacconi, Prattica di musica . . . (Venice: Girolamo Polo, 1592), p. 8.
134From Jacobus Faber Stapulensis [Jacques LeFebvre], Elementa musicalia (1496), III, i; quoted in Hugo Riemann, History of Music Theory, Books I and II; Polyphonic Theory to the Sixteenth Century, trans. with a preface, commentary, and notes by Raymond H. Haggh (Lincoln, Nebraska: University of Nebraska Press, 1962), pp. 283-284. In a similar vein, LeFebvre also finds the major third, and the major and minor sixth not to be consonances. (The assignation of different ratios by various authors to the same consonance is typical of the period and is the result of different theories of tuning.)
135From the Latin ottonarius meaning consisting of eight. Of course, the ratio for the minor sixth (8:5) was among the parts of the ottonario. For a complete list of the consonant intervals obtainable from the senario as supplemented by the ottonario, see Zarlino, Dimostrationi harmoniche, p. 84 [misnumbered p. 72].
136Boethius, De institutione musica, I, i, p. 178; trans. in Strunk, Source Readings, pp. 79-80.
137". . . la Intelligentia ò Intelletto, ò Ragione che la vogliamo dire, hà origine (seconda la dottrina di Aristotele) da i Sensi; poiche non si trova cosa veruna essere, overo essere stata nell'Intelletto; . . . che non sia ò prima non sia stata in essi." Zarlino, Sopplimenti musicali, I, xiii, p. 37.
138The influence of Aristoxenus and Ptolemy did not, of course, begin with the translations commissioned by Zarlino. Earlier theorists, such as Gafori, were acquainted with their teachings and similarly chose a balance between reason and sense.
139"I primi lasciavano il Senso da un canto, ad un certo modo nel ricever la ragione de i Suoni; & li secondi lasciavano la Ragione & seguitavano il Senso. Et perche era cosa difficile, anzi impossibile, il sapere essattamente conoscer nella Qualità le Differentie, che si trovano tra i Suoni gravi & gli acuti; lasciandosi l'una di queste due cose da un canto, ò il Senso ò la Ragione, come veri Giudici di cotal cosa; . . . però giudicò Tolomeo gran Mathematico & Filosofo; . . . che fusse bene, nel far giudicio de i Suoni, che si dovesse seguitare il Senso, come principale; ma accompagnarli anco la Ragione; l'una per poter conoscer bene, quali erano Dissonanti tra loro ò Consonanti, ò quale di due fosse più acuto ò più grave dell'altro, & l'altro per conoscere, di quanto l'uno dall'altro erano distanti ò differenti di proportione, & quanto l'uno avanzasse l'altro nella Quantità & nella Qualità. . . ." Zarlino, Sopplimenti musicali, I, xv, p. 41.
140Zarlino, for one, discusses his writings at length. See ibid., I, x-xv, pp. 31-42 et passim.
141Aristoxenus, The Harmonics of Aristoxenus, trans. with notes, introduction, and index by Henry S. Macran (Oxford: Clarendon Press, 1902), pp. 193-194.
142Ibid., p. 189.
143Lippman, Musical Thought in Ancient Greece, p. 149.


