The usefulness of sketch studies for analysis has been a topic of some controversy in recent years, particularly since the exchange that took place in 19th Century Music in 1978 between Douglas Johnson and others.1 In his arguments against the use of sketches for analysis, Johnson raised what one writer noted as, "questions about the very nature of analytical thinking about music."2 The basic questions are ones which many theorists and musicologists have debated: what information is relevant to an analysis? To what extent is analytical information contained only in the finished score itself? If the score alone is sufficient, then analysts may proceed along the path of formalism with the emphasis on internal logic, coherence, and organic unity. If other sources, such as sketches or drafts, are admitted for analysis, however, additional questions arise: What is the relationship between a sketch and a finished composition? Will analysis of sketches yield relevant information about the corresponding piece? Can we posit a one-to-one correspondence between notes in the sketch and notes in the finished score?
Writings on sketch studies generally focus on the era of tonal composition, particularly the music of Beethoven. In Figures 1 and 2, I have summarized the views on the relationship between sketch studies and analysis that have arisen in discussions of this repertoire. The chart that supports the use of sketch study, Figure 1, has three sections: the general uses of sketches, which do not provoke argument; uses which have analytical components; and uses which are specifically analytical. Those in favor of sketch study basically subscribe to the notions that: (1) sketches are worthy objects in and of themselves for study, even if no direct relationships to finished pieces exist; and (2) analysis is a difficult process and analysts should use all available resources. The analytical categories of Figure 1 are countered in Figure 2. Those against sketch study argue from the basis that: (1) analysts can never be sure that their application of analytical insights from the sketches into finished pieces is accurate; and (2) if analytical information in the sketches cannot be found in the piece itself, then such information is irrelevant.
Figure 1: Arguments for the Use of Sketches for Analysis
General
1) to date and establish chronology of finished work;
2) to unearth unfinished or planned projects, and unpublished works;
3) to uncover copying errors, corrections, omissions, or alternate versions for use in critical editions or performing scores;
4) to complete unfinished works;
5) to uncover symbols, programmatic associations, literary references, or biographical details about composer;
6) to reveal the initial impulse of genius.General and Analytical
7) to reveal working methods and compositional processes of composers;
8) to explore dead ends or abandoned solutions to compositional problems by comparing earlier and later versions, and to determine how the finished work is more or less appropriate than earlier versions.Specifically Analytical
9) the finished piece interprets the sketches—useful analytical information flows both ways;
10) to confirm an existing analysis;
11) to solve problems from difficult passages encountered in analysis by examining materials in embryonic, simpler versions;
12) to highlight surface relationships completely missed in analysis;
13) to uncover common sources or derivations for material not associated on the surface, or in analysis, to demonstrate underlying unity and coherence.
Figure 2: Arguments against the Use of Sketches for Analysis
1) sketches tell about the composer, not the work;
2) when completed, a work has a separate, self-contained existence, with all the information necessary for its own analysis;
3) substituting a sketch for the finished piece posits relationships composer may have abandoned, or the goals of the sketch and piece may be completely different, and the sketch evidence may not be applicable or may even be irrelevant or misleading in the context of the finished piece;
4) sketches are only shorthand and piecemeal; they lack coherence and organic unity, and incompleteness makes it questionable to attribute significance;
5) if sketches differ from finished work, differences can only be explained by a theory, with predictive power, of why the changes were made—such a theory based on composer's intention or authority from sketches is untenable;
6) positing direct, causal relationships from sketch to finished piece reveals bias towards unified, unambiguous, finalized works, which, in opera, for instance, may be unjustified;
7) even if sketches reveal shared sources for dissimilar and unassociated surface material, that information does not alter the analysis of the finished work.
In the music theory community, writers such as Allen Forte and Carl Schachter have used sketches to confirm their analyses of finished works. Forte used the composer's sketches in his analysis of Beethoven's compositional technique in the Piano Sonata Op. 109; Schachter analyzed sketches from Beethoven's Piano Sonata Op.14/1 to point out relationships in the piece more easily discerned in their earlier, unadorned forms.3 This methodology—using sketches in the context of an already completed analysis of the finished piece—tends to be informal rather than a systematic study of all possible relationships between the sketches and the piece. Although similar uses of sketches crop up in many analytical writings by theorists, it is interesting to note that in their book, Analysis (expanded from Bent's entry in The New Grove Dictionary of Music and Musicians), William Drabkin and Ian Bent mention sketch study only briefly, in relation to Nottebohm's writings on Beethoven's music.4
While most of the sketches-versus-analysis debates center on tonal music, sketches have also been used as aids for analysis of twelve-tone music by many writers. Indeed, twelve-tone compositions seem to be one area in which sketches have a demonstrable analytical impact. For instance, it is often difficult when analyzing twelve-tone pieces to decide which rows are being used. If, however, sketches with row indications or order position numbers exist, in the form of row charts, sketches of rows grouped into themes, motives, or accompaniment patterns, or in drafts, the task is greatly facilitated. Furthermore, the composer's own row indications and order position numbers seem to offer a definitive reading, even the possibility of ascribing intention in the analysis.
An example of the use of sketches in twelve-tone analysis appears in the writings of Martha Hyde.5 In her dissertation and related articles, Hyde set out to solve the problem of defining harmony in Schoenberg's twelve-tone music by using the pitch-class set theory relationships posited by Allen Forte.6 In her view, Schoenberg's rows are regarded as compendiums of pitch-class sets which can be exploited in many arrangements: transposed or inverted, ordered or unordered, between adjacent or nonadjacent notes, and within one row or between different rows. Hyde uses sketches, charts, and drafts showing individual rows, combinations of rows, row reorderings, and combinatorial groupings as aids to analysis. In effect, she analyzes the sketches, using Schoenberg's own indications to solve the problems of row identification and segmentation of significant pitch-class sets. Because in a fully chromatic context with multiple row presentations segmentation can be problematic, the analysis of the sketches guides the analysis of the pieces. A one-to-one correspondence between the two is posited, with the piece interpreted as a "realized" sketch in which the same relationships occur under the same conditions.
Hyde's sketch-derived analysis also invokes the authority of Schoenberg, who, although he did not use pitch-class set terminology, grouped notes in his sketches with brackets and slurs. The equivalences indicated by these groups are explained in pitch-class set terms by Hyde. She concludes that Schoenberg was systematic about his use of harmony, contrary to earlier opinions, that he did so intentionally and within the range of equivalences posited by pitch-class set theory, and that these set relationships are themselves related by the same equivalences to the source twelve-tone row of each piece.
Hyde and other twelve-tone analysts have been influenced by a tradition of compositional theory stemming from Milton Babbitt in which descriptions of precompositional row arrangements become synonymous with analyses of pieces.7 In this view, a natural course for analysis of twelve-tone music is to use sketches as the models for the order position and pitch-class set manipulations of the row in an effort to uncover the compositional strategies unfolded in the course of a piece. The sketch information is generally accepted as useful and relevant for analysis in this context.
In his well-known critique of twelve-tone analyses, Edward Cone asserted that composers in the Babbitt circle tend to apply the registral and temporal equivalences of their own compositional criteria to their analyses of older music in which these criteria might not apply.8 Although Cone did not refer to sketches, the same charge might be levelled against analyses of sketches from older music. For instance, is Hyde justified in her interpretations of equivalences based on pitch-class sets drawn from grouping indications in Schoenberg's sketches, or are these relationships which Schoenberg may not have intended, or, if he intended, may have used to quite different ends? In more general terms, is it valid to invoke the authority of the composer from sketches when positing relationships based on equivalences not explicitly set out as such? And, even where composers analyze their own sketches, should the information be considered relevant for analysis, or only for defining steps in the compositional process?
Berg's twelve-tone music offers an intriguing case for discussing the relevance of sketch studies for analysis. Most of Berg's sketch material is found at the Austrian National Library in Vienna, and is available firsthand to visiting scholars and, remotely, via microfilm. Therefore, access to most of the material is not difficult, and many scholars have availed themselves of the ease of examination. Sketches exist for all of Berg's published pieces, as well as for student works and an unfinished symphony from 1913. A catalogue of Berg's sketches and writings prepared by Rosemary Hilmar (1980), who was in charge of the Berg materials at the time, was published as the Alban Berg Studien, Vol. 1, and, although not without errors, it serves as a convenient starting point.9
For Berg, perhaps more so than other composers, sketch studies have revealed much about the man and his compositional methods. From the sketches, writers such as George Perle, Douglas Jarman, Douglass Green, Patricia Hall, and Brenda Dalen have unearthed secret, "hidden" autobiographical programs, quotations, numerology, and symbols. In addition, Berg sketch study has led to several tangible results: (1) the revelation of the hidden song in the final movement of the Lyric Suite; (2) the plan of the "Film Music" Interlude in Lulu, and, (3) the completion of Lulu by Friedrich Cerha.10 In terms of information about the composer's life and his compositional practice, sketch study into Berg's music has been an unqualified success.
For his twelve-tone music, Berg left row charts of considerable detail. Sketches include rows and derived material in row charts identified by order position numbers and transposed to every degree of the chromatic scale, and in drafts with order position numbers and often lists of the twelve notes with some crossed off. Berg's sketches may also be supplemented by his own analytical notes; with regard to the Lyric Suite, for instance, Berg wrote an extended letter to Schoenberg outlining his row manipulations and included a longer description in his "Nine Pages on the Lyric Suite."11 Other letters and writings by Berg contain theoretical discussions and examples of passages in his music, and the analyses given in Willi Reich's books and articles reportedly stem from Berg's own written notes.12
On a very basic level, Berg's sketches aid the analyst in identifying the rows used and how these rows are arranged on the surface. Berg's derivations of material from rows are often quite complicated, and are based on abstract number systems, representations of names in musical notes, and motivic rhythmic relationships. In many respects Berg's row procedures are not unlike the secret programs, numerology, and symbols in his music. Though of interest, these hidden references are ultimately irrelevant to analysis. For instance, the "meaning" of the note group, A, ,B,F, in the Lyric Suite as the initials of Alban Berg and Hanna Fuchs-Robettin is useless information to the analyst. If the sketches are to be used for analysis, we must determine whether the information they provide is useful and relevant.
,B,F, in the Lyric Suite as the initials of Alban Berg and Hanna Fuchs-Robettin is useless information to the analyst. If the sketches are to be used for analysis, we must determine whether the information they provide is useful and relevant.
One issue that arises is whether Berg's notated derivations of material from rows constitute sufficient evidence for positing relationships in the finished piece. This issue is behind a controversy that has surrounded the derivation of rows from the principal or "basic row" in Berg's opera Lulu. In 1959, George Perle questioned Willi Reich's 1936 explanation of the opera's musical language. Reich's contention, apparently following Berg's own statements and writings, was that the derivation of all material from the basic row guarantees unity in the opera.13 Perle countered that, due to the esoteric nature of the supposed row relationships, this assertion is erroneous, and that unity arises only from invariant relationships established among materials in the opera itself, rather than by their purported source in the basic row. In other words, the derivations shown in the sketches are irrelevant for analysis.14
The controversy centers on the derivation of the character rows of Alwa, the Acrobat, Schoolboy, and Dr. Schön from the basic row of the opera.15 The sketches for Lulu clearly show that Berg derived the rows associated with the different characters in the opera from the basic row; they are written out labelled with order position numbers of the basic row. The derivations are accomplished by numerical sequences performed on the order positions of the basic row, as shown in Example 1.16
Example 1: Derivations of character rows in Lulu.

Alban Berg Lulu, Copyright 1964 by Universal Edition A.G., Wien, Copyright renewed, Revision © Copyright 1985 by Universal Edition A.G., Wien, All Rights Reserved, Used by permission of European American Music Distributors Corporation, sole U.S. and Canadian agent for Universal Edition A.G., Wien.
For instance, the row associated with Alwa is derived by taking every seventh note of the basic row, resulting in the order position succession 0 7 2 9 4 B 6 1 8 3 A 5. For the row of the Acrobat, every second note is extracted from the basic row, and for the Schoolboy row, every third note is extracted; in both rows, adjustments are made to arrive at all twelve order positions. Dr. Schön's row is created from a pattern of extractions according to the series, +2, +3, +4, +4, +3, +2, +2, +3, +4, +4, +3.
Despite Berg's sketch notations, the relationships between the derived rows and the basic row are often difficult to perceive. Douglas Jarman, in reviewing both Reich's and Perle's positions, has commented that if the row derivations are not directly and audibly projected on the surface, they are irrelevant.17 Certain row relationships are presented on the surface; for instance, the order position series which generates Dr. Schön's row is revealed at his death, as shown in Example 2.
Example 2: The Basic Row and Schön rows at Schön's death in Lulu II/i.

Alban Berg Lulu, Copyright 1964 by Universal Edition A.G., Wien, Copyright renewed, Revision © Copyright 1985 by Universal Edition A.G., Wien, All Rights Reserved, Used by permission of European American Music Distributors Corporation, sole U.S. and Canadian agent for Universal Edition A.G., Wien.
Here the basic row is stated three times, with the notes of the Dr. Schön row separated registrally and instrumentally (upper voice treble clef in the example). Thus, the relationship between the two rows is revealed by the relative rhythmic proportions of the Dr. Schön row. Other row derivations are, however, not explicitly set out in the music. But should Jarman's criteria of audibility be the final arbiter of the relevance of the derivations, and by extension, of the sketches?
In an earlier article, I have shown that the extraction of every seventh note, or the multiplicative order position operation "M7," which creates Alwa's row, yields invariances with the basic row and with the derivation of Dr. Schön's row.18 As shown in Example 1, the even number order positions between the basic row and Alwa's row are held invariant (these are circled in the example). The numerical series that creates Dr. Schön's row groups in twos or threes into gradations of sevens, which allows for an invariance of two notes per trichord with Alwa's row (these are shown with circles and vertical lines at the bottom in Example 1).19 The invariances between the Alwa row, basic row, and Dr. Schoen's row are exploited in the opera, particularly in the "Film Music" from Act II (mm. 670-74), where they are associated with one of the basic cells of the opera (E-A- -
-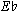 ) and to the Hauptrhythmus. Thus, the derivational procedures displayed in the Lulu sketches are useful in that they can explain invariances and relationships uncovered by analysis. I would, therefore, qualify Perle's comments by saying that, while relationships are determined by invariances between materials in Lulu, the derivations revealed by the sketches directly cause those invariances. In this case, the sketches are at least useful for positing a theory about such relationships.20
) and to the Hauptrhythmus. Thus, the derivational procedures displayed in the Lulu sketches are useful in that they can explain invariances and relationships uncovered by analysis. I would, therefore, qualify Perle's comments by saying that, while relationships are determined by invariances between materials in Lulu, the derivations revealed by the sketches directly cause those invariances. In this case, the sketches are at least useful for positing a theory about such relationships.20
Another Berg work in which the sketches pose interesting problems for analysis is the Violin Concerto. This piece has long been regarded as a combination of twelve-note and tonal aspects, either in a fusion of the two or as an unresolved opposition of the two worlds, the latter associated with the program of the life and death of a young girl, Manon Gropius. The difficulty of analyzing the musical language in the concerto leads us to search for answers in the sketches.
Berg's sketches for his Violin Concerto contain not only row tables and derivations of material from the rows, but also include analyses by Berg of his own materials. Some of these sketches are transcribed in Example 3.21
Example 3: Transcribed sketches from the Violin Concerto.
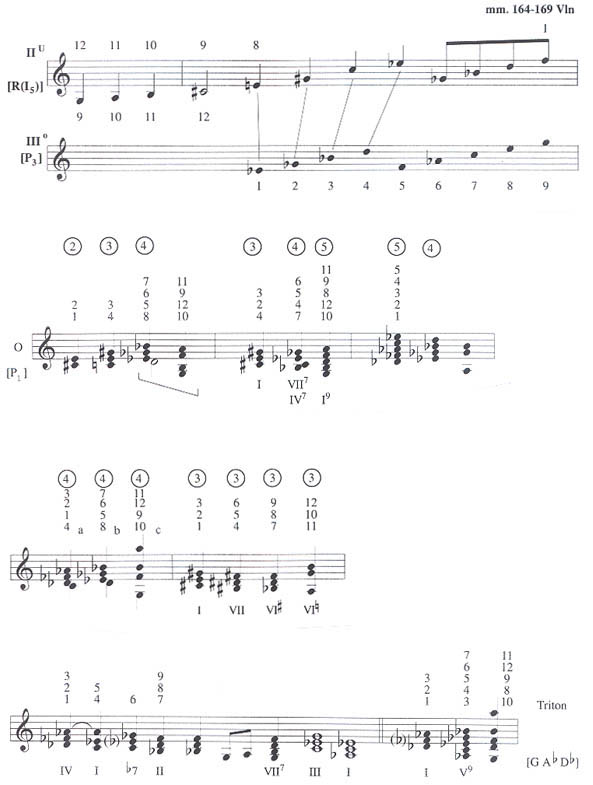

Berg Violin Concerto, Copyright 1936 by Universal Edition, Copyright renewed, All Rights Reserved, Used by permission of European American Music Distributors Corporation, sole U.S. and Canadian agent for Universal Edition.
In derivations of trichordal row segments, for instance, shown in Examples 3c (second bar), 3d, and 3f, Berg adds both order position numbers and tonal Roman numerals. We may feel justified, then, in regarding the concerto as a realized version of the sketch material. For instance, the famous passage of triads at the beginning of the first movement, shown in Example 4, might be analyzed tonally in G minor.
Example 4: Violin Concerto, mm. 10-14.

Berg Violin Concerto, Copyright 1936 by Universal Edition, Copyright renewed, All Rights Reserved, Used by permission of European American Music Distributors Corporation, sole U.S. and Canadian agent for Universal Edition.
The related sketch is shown in Example 3e from row P1; although Berg does not indicate Roman numerals, such indications for the row I6 in Example 3f (second bar) may be used as justification for this reading. Is this tonal analysis relevant, however, or do the order position attributes of these triads, also indicated in Berg's sketches, constitute a more meaningful analysis? In the first case, the row itself is irrelevant to the tonal system and the analysis, and, in the second the row is the basis of the analytical relationships.22
In the course of writing the Violin Concerto, Berg had developed most of his row material before deciding on a chorale. Sketches show that he first experimented with a chorale made from the row itself, but eventually he chose the Bach chorale Es ist Genug, at least partially because of the invariance between its opening four notes and the final four notes of the row, as shown in Example 5.23
Example 5: Row of Violin Concerto and opening of Es ist Genug.

Berg Violin Concerto, Copyright 1936 by Universal Edition, Copyright renewed, All Rights Reserved, Used by permission of European American Music Distributors Corporation, sole U.S. and Canadian agent for Universal Edition.
How are we to analyze this relationship between a tonal chorale and a twelve-tone row? The sketches again show both tonal and serial interpretations. As before, in a tonal interpretation, the row is irrelevant; in an order position interpretation, the tonality is irrelevant. Perhaps the correspondence between row and chorale unlocks a meeting point between the twelve-tone and tonal systems explainable only by a combined definition. Or would such an interpretation posit a false unity that does not adequately explain the dichotomy of a tonal chorale in a twelve-tone piece?
Consider a passage in the variations following the presentation of the Bach chorale, measures 164-169, shown as Example 6. Given the evidence in the sketches, we may feel justified in assigning Roman numerals and keys to the chords in this passage, especially considering its proximity to the tonal chorale. A tonal analysis taken from a recent book by Anthony Pople on the Violin Concerto appears below the music in Example 6.24
Example 6: Violin Concerto, II, mm. 164-169. serial analysis (order positions 0-B), and tonal analysis by Anthony Pople.

©Cambridge University Press 1991. Reprinted with the permission of Cambridge University Press.
Berg Violin Concerto, Copyright 1936 by Universal Edition, Copyright renewed, All Rights Reserved, Used by permission of European American Music Distributors Corporation, sole U.S. and Canadian agent for Universal Edition.
In Pople's analysis, the two tonal areas appear to be F and  . Precedents for semitonal key areas occur in Schoenberg's late tonal music. The tonal analysis in the Violin Concerto, however, apparently applies only to momentary dominant to tonic motions, lasting only for the duration of the chords. In a larger context, the Violin Concerto has been described as moving from the key of G to
. Precedents for semitonal key areas occur in Schoenberg's late tonal music. The tonal analysis in the Violin Concerto, however, apparently applies only to momentary dominant to tonic motions, lasting only for the duration of the chords. In a larger context, the Violin Concerto has been described as moving from the key of G to  ; evidence for these keys is, however, as fleeting as the tonal areas in Pople's indications. The usefulness of such assertions to analysis seems extremely limited.
; evidence for these keys is, however, as fleeting as the tonal areas in Pople's indications. The usefulness of such assertions to analysis seems extremely limited.
An alternative analysis of the passage is the detailing of the order positions of the rows. The violin melody in Example 6 results from an intertwining of two rows: combined rows P3 and either R(I5) or Pl (since the row is equivalent to its own rotated retrograde inversion). The two rows extend past the end of the passage to m. 175, and at m. 178, three rows are similarly intertwined in the continuation of the violin melody. We may also supply order positions and row attribution to the other parts in Example 6, following sketches in which Berg reordered row segments and added or omitted notes. When we have completed the identification, however, we find that the information does not tell us much about the passage.
Since the sketch information seems to be of limited use for analysis, we may have to search elsewhere for answers to this passage. Briefly, I will outline a possible solution. My analysis stems not directly from the sketches, but from examination of all of Berg's music, in the context of an early letter by Berg to Schoenberg and the theories of George Perle.25 I consider Berg's music to consist of interacting collections derived from interval cycles, as shown in Example 7.
Example 7: Violin Concerto, II, mm. 164-69, a cyclic analysis.

Berg Violin Concerto, Copyright 1936 by Universal Edition, Copyright renewed, All Rights Reserved, Used by permission of European American Music Distributors Corporation, sole U.S. and Canadian agent for Universal Edition.
The passage is oriented around 3-cycle-based chords (in tonal terms, "diminished seventh chords" or set class [0, 3, 6, 9]); similar 3-cycle chords unfolded in mm. 165 and 169 are marked by asterisks. Between the asterisks, contrasting 5-cycle and whole-tone based chords appear. The open noteheads are "consonant" notes, while filled-in noteheads are "dissonant" notes which compel the melodic lines and harmonic successions forward.26 For instance, note that the initial low C (mm. 164-65), a local consonance in a 5-cycle A-D-G-C, begins as a dissonance in a larger Tl 3-cycle context ( -E-G-
-E-G- ), but becomes consonant in a 5-cycle context (m. 166, C-F-
), but becomes consonant in a 5-cycle context (m. 166, C-F- -
-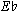 -
-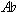 ) and leads by interval 5 to F; in the corresponding note pair
) and leads by interval 5 to F; in the corresponding note pair  -
- (mm. 167-68), the
(mm. 167-68), the  begins as a dissonance in a T2 3-cycle (D-F-
begins as a dissonance in a T2 3-cycle (D-F-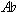 -B), but turns into a consonance as part of the closing bass Tl 3-cycle
-B), but turns into a consonance as part of the closing bass Tl 3-cycle  -
- -G-E.
-G-E.
Although the passage is based on cycles, Berg incorporates both "tonal" and row elements. The cyclic chords create the illusion of tonal function by exploiting their tonal appearance, particularly the 3- and 5-cycle based chords, and motion by intervals 5 or 7 in the bass. The rows are invoked by the identity of chords with triadic row segments, as well as the aggregate completion possibilities of the cycles. For instance, the 3-cycle chords progress through the three transpositions to make up an aggregate, from a chord based on  (Tl), to C (TO), to D (T2) and back to
(Tl), to C (TO), to D (T2) and back to  (Tl).
(Tl).
To conclude, I will refer to the categories for sketches proposed by Philip Gosett.27 First, sketches may be useful if they are confirmatory; that is, if they confirm relationships analyzed in the score. Second, they may be suggestive, allowing the analyst to explore different angles on relationships already found in the score. The problematic area for sketches is Gosset's third category, called "conceptual," where sketches uncover posited relationships that have been substantially altered, transformed beyond recognition, or placed in contexts in which they may no longer be meaningful in the corresponding piece. Particularly in passages from the Violin Concerto, Berg's sketches showing tonal and row-related origins and functions of material yield conflicting and inconclusive analyses. The transformation that has occurred between sketch and finished product renders the sketch information of limited use for analysis and alternative solutions must be sought. Sketches may prove useful for analysts when used in controlled situations after thorough analysis, but the conceptual and musical distance that separates the sketch from the finished piece should not be underestimated.
1Douglas Johnson, "Beethoven Scholars and Beethoven's Sketches," 19th Century Music 2, no. 1 (1978): 3-17; Sieghard Brandenburg, William Drabkin and Douglas Johnson, "On Beethoven Scholars and Beethoven Sketches," 19th Century Music 2, no. 3 (1979): 270-279; see also Taylor A. Greer, "Comment: The Relation Between Sketch Study and Analysis: A Reply to Johnson," In Theory Only 6, no.7 (December 1982): 13-18; and, Joseph Kerman, "Sketch Studies," 19th Century Music 6, no. 2 (1982): 174-180.
2Taylor A. Greer, "Comment: The Relation Between Sketch Study and Analysis: A Reply to Johnson," In Theory Only 6, no. 7 (December 1982): 14.
3See Allen Forte, The Compositional Matrix (Baldwin, NY: Music Teachers National Association, 1961; reprint ed., New York: Da Capo Press, 1974); and Carl Schachter, "Beethoven's Sketches for the First Movement of Op. 14, No. 1: A Study in Design," Journal of Music Theory 26, no. 1 (Spring 1982): 1-21.
4Ian Bent and William Drabkin, Analysis. The Norton/Grove Handbooks in Music (New York: Norton, 1987), 34-35.
5Martha Hyde, "Schoenberg's Concept of Multi-dimensional Twelve-Tone Music: A Theoretical Study of the Music and Compositional Sketches" (Ph.D. Dissertation. Yale University, 1977); "The Roots of Form in Schoenberg's Sketches," Journal of Music Theory 24, no. 1 (Spring 1980): 1-36; and Schoenberg's Twelve-Tone Harmony: The Suite Op. 29 and the Compositional Sketches (Ann Arbor: UMI Research Press, 1982).
6Forte's theory is set out in his The Structure of Atonal Music (New Haven: Yale University Press, 1973).
7The initial offerings are Milton Babbitt, "Twelve-Tone Invariants as Compositional Determinants," Musical Quarterly 46 (1960): 246-59; and "Set Structure as A Compositional Determinant," Journal of Music Theory 5, no. 1 (1961): 72-94.
8Edward Cone, "Beyond Analysis," Perspectives of New Music 6, no. 1 (Fall/Winter 1967): 33-51.
9Rosemary Hilmar, Katalog der Musikhandschriften Schriften und Studien Alban Bergs Im Fond Alban Berg und der Weiteren Handschriftlichen Quellen im Besitz der Österreichischen NationalBibliothek. In Alban Berg Studien. Bd. I. Edited by Franz Grasberger and Rudolf Stephan (Vienna: Universal Edition, 1980).
10George Perle, "The Secret Program of the Lyric Suite," International Alban Berg Society Newsletter 5 (June 1977): 4-12; "The Film Interlude of Lulu," International Alban Berg Society Newsletter 11 (Spring 1982): 3-8; Douglass Green, "Berg's De Profundis: The Finale of the Lyric Suite," International Alban Berg Society Newsletter (June 1977): 13-23; and Friedrich Cerha, Arbeitsbericht (Vienna: Universal Edition, 1979).
11Juliane Brand, Christopher Hailey, Donald Harris, The Berg-Schoenberg Correspondence (New York: W.W. Norton, 1987); Donald Harris and Mark Devoto, "Berg's Notes for the Lyric Suite," International Alban Berg Society Newsletter 2 (January 1971), pp. 3-5; Alban Berg, "Neun Blätter zur "Lyrische Suite für Streichquartet," in Alban Berg: Bildnis im Wort: Selbstzeugnisse und Aussagen der Freunde, ed. W. Reich (Zurich: Die Arche, 1969): 45-54; and Ursula Rauchhaupt, Schoenberg, Berg, Webern: Die Streichquartette, Eine Documentation (Hamburg: Deutsche Grammophon Gesellschaft, 1971).
12Willi Reich, Alban Berg, trans. Cornelius Cardew (London: Thames and Hudson, 1965).
13See Willi Reich, "Alban Berg's Lulu," Musical Quarterly 22, no. 4 (October 1936): 383ff.
14 See George Perle, "The Music of Lulu: A New Analysis," Journal of the American Musicological Society 12, nos. 2-3 (Summer/Fall 1959): 185ff; The Operas of Alban Berg, Volume II: Lulu (Berkeley: University of California Press, 1985): 157-61.
15Another row included in the controversy, with a more complex pedigree, is that of the Countess Geschwitz, whose materials are derived from a row created by taking every fifth note of the basic row. See Douglas Jarman, "Countess Geschwitz's Series: A Controversy Resolved?" Proceedings of the Royal Music Association 107 (1980-81): 111-118.
16The numbers in Example 1 are order position numbers (by convention, A = 10, B = 11).
17Douglas Jarman, The Music of Alban Berg (Berkeley: University of California Press, 1979), 125.
18Dave Headlam, "The Derivation of Rows in Lulu," Perspectives of New Music 24, no. 1 (1985): 198-233.
19In fact, Alwa's and Dr. Schoen's row share the same trichordal and hexachordal set-classes.
20This interpretation of sketch evidence in the context of a theory about the nature of the posited relationships satisfies the conditions set out by Leonard Meyer for using sketches in analysis. See Explaining Music (Berkeley: University of California Press, 1973), 78.
21Sketches are from F 21 Berg 85/I in Hilmar's catalogue (1980). "O" = Original (prime), "U" = Umkehrung (inversion).
22Perle has commented that Berg's apparently tonal criteria for added notes in the concerto and other works represents a problem for the classical interpretation of the twelve-tone system: "Harmonic relations in twelve-tone music cannot in general thus depend upon a borrowed harmonic language, based upon premises that have no general meaning in the twelve-tone system." See Serial Composition and Atonality, 5th Ed. (Berkeley: University of California Press, 1981), 91.
23Anthony Pople. "Berg, Violin Concerto," in Cambridge Music Handbooks, Gen. ed. Julian Rushton (Cambridge: Cambridge University Press, 1991), 31.
24 Ibid., 86-87. Pople also discusses the serial and tonal indications in Berg's sketches to the Violin Concerto, and presents serial and tonal/referential collection analyses in separate chapters (3 and 5). Although Pople shows a possible tonal interpretation, he does not invoke the sketches as a justification; rather, the tonal interpretation reflects "how the music . . . may be understood in the context of a wider repertoire." His comments that the tonal analysis does not show large-scale unity echo Jarman's statement that tonality has an articulative rather than a unifying function in Berg's music. See Douglas Jarman, The Music of Alban Berg (Berkeley: University of California Press, 1979), 16.
25A complete account of a theory and analysis for all of Berg's music will appear in my book The Music of Alban Berg (New Haven: Yale University Press, forthcoming).
26Cyclic collections in their "pure" formrelatively rare occurrencesare subsets of [0, 2, 4, 6, 8, A] for whole-tone collections, which usually subsume 4-cycle, [0, 4, 8]-based collections, and [0, 3, 6, 9] for 3-cycle collections. Five-cycle collections are more fragile in their cyclic guises, and depend on the contextual presence of interval 5s proportional to their increase in number of elements. Cyclic-based collections include "non-chord" tones, which create instability and a forward drive for "resolution," which never arrives in unequivocal form, and thus accounts for the affinities between Berg's music and the preceding "romantic" composers. The difference between cyclic-based collections and pitch-class sets is the distinction between chord tones and non-chord tones, but this distinction does not preclude pitch-class set type relationships.
27Philip Gosset, "Beethoven's Sixth Symphony: Sketches for the First Movement," Journal of the American Musicological Society 27 (1974): 259ff.


