Music is an aural art, yet too often we teach our students to relate to it with their eyes, rather than with their ears. Whether listening to the radio or recordings, or watching film or television, or at a symphony or chamber concert, the opera, ballet, or a rock concert, they are usually without the benefit of a score. The following essay is offered as one possibility for helping our students become better listeners; the goal is to change them from being passive, uninvolved listeners to being involved, active ones.
After teaching primarily visual analysis to music majors for several years, I gradually began to change my emphasis from working with scores to working with recordings. As my students grew more comfortable with the experience I increased the number of recordings heard in class, so that today I spend around two thirds of my class time with aural analysis. A well-rounded course in analysis might offer one term of visual analysis, a second term based on looking while listening, and a third term based exclusively on listening.
I have concentrated my efforts on homophonic music, as it has proven to be more accessible for the purpose of aural analysis. In particular, the piano sonatas, string quartets, symphonies, and concertos of Haydn, Mozart, and Beethoven have proven to be especially successful. They offer some of the clearest examples available, and at the same time expose our students to major repertoire. Mozart's "Eine Kleine Nachtmusik", his piano sonatas in C Major (K.545) and Bb Major (K.333), and his 10th, 29th, 39th, 40th, and 41st symphonies are all very accessible works. Once comfortable with the listening process, the works of Beethoven, Berlioz, Schubert, Mendelssohn, Dvorák, and Brahms, help to broaden the spectrum. I also bring vernacular music into the classroom from time to time as most students relate to it particularly well, and they learn basically the same skills from it as they do from the classical repertoire.
LaRue Timelines
I have been teaching analysis based on the concepts of Jan LaRue for the past thirty-two years, having worked with him between 1962-3 at New York University, and my approach to aural analysis is heavily based on his concepts.1 LaRue's contributions to the field of analysis are twofold. First, he asks us to consider all aspects of a composition, SOUND, FORM (OR GROWTH), HARMONY, RHYTHM, and MELODY, rather then putting the emphasis mainly on form and harmony, more typical of many analytical theorists.2 He also places special importance on the area of melodic analysis, an area too often overlooked by those more concerned with "form and analysis." Second, he asks us to consolidate as much analytical information as possible into a graphic presentation.
LaRue's approach to analysis is fundamentally architectural. He lays out on graph paper the basic design of a movement, "timeline," which ends up functioning something like the designs for a building. LaRue's deceptively simple concept, based on the idea that a single picture is worth a thousand words, is comprehensive in scope.
As I have used LaRue's analytical concepts all of my professional life, I am no longer sure where I begin to interject my own interpretation into his. My approach might best be described as a practical application of his unique system, based on both his lectures and his text. LaRue's approach allows for considerable detail, and is extremely useful when working with graduate students. When working with undergraduates it seems advisable to keep things on a simpler level, especially when involving them in aural analysis. The following approach is intended for an undergraduate course in aural analysis, and therefore does not go into as much detail as LaRue's system is capable of.
Since LaRue's system is fairly demanding, it takes some energy on the part of the user to become comfortable with his approach. But once understood, it will be seen that LaRue's symbolic guide to motivic analysis gives us the tools that are necessary to discuss the manner in which musical motives and phrases work. A major advantage of the system is that it allows us to go into as much (or as little) detail as we desire. A LaRue timeline gives us the ability to grasp in a single visual image the essence of any given musical composition. While writers such as J. W. N. Sullivan tended to present musical analysis in subjective, poetic imagery, LaRue presents musical analysis in objective, specific imagery.3 Whereas Sullivan referred to the late quartets of Beethoven as "spiritual experiences," LaRue offers us tools that can help us better understand why they may be so. A timeline of one of the late quartets will show that Beethoven has taken a form that previously was fairly straightforward and predictable, and has transformed it into something considerably more abstract. This can be seen in the work's overall length, (the addition of transitions between movements, the addition of lengthy slow introductions, the inclusion of extended codas, and the extended length of the individual sections within each movement), its motivic complexities, and its harmonic wanderings. The timeline further demonstrates Beethoven's ability to sustain continuing variety while maintaining both economy and continuity. I am grateful for the writings of Sullivan, but my comprehension of his observations became much more tangible after seeing them presented in the form of a timeline.
Over the years I have come to realize that LaRue's timelines go far beyond simply helping students of analysis. They are just as useful to the performer who needs to memorize a concerto, or to the conductor who wishes to conduct without score.
* * *
Because works in sonata-allegro form are certainly one of the most important forms for students to grasp, and because LaRue's timelines have proven especially effective here, this is the area in which I have concentrated much of my own teaching of analysis. The primary goal of a timeline is to show in graphic form the large, middle, and small-scale motion of a work; if this can be done on one page, so much the better. A work in sonata-allegro form takes on the following general format:
| (1) | the largest structure is the exposition, development, and recapitulation, with the possible inclusion of a slow introduction and a coda at the end. |
| (2) | the middle ground is the primary, secondary, and closing themes, and the transitions that separate them. |
| (3) | the smallest level of analysis concerns the motives upon which the middle ground material is based. This is often as short as four notes, such as the opening gesture of Beethoven's fifth symphony. |
A diagram of a typical movement in sonata-allegro form might take on the following format (see Example No. 1). Melodic material is presented above each line; harmonic material is presented below; (developmental material is shown by question marks). A key area without parentheses indicates that we are in that key, normally established by a V-I cadence; a key area in parentheses indicates that we are on the key, one which has not been established by a cadence. (In the following diagram, P stands for "primary", T for "transitional", S for "secondary", and C for "closing".)
Example No. 1. "A typical movement in sonata-allegro form."
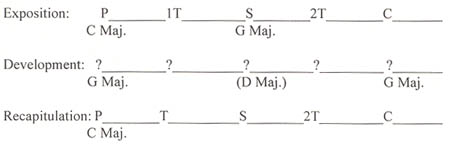
There is one area concerning sonata-allegro form that has always puzzled me in the writings of others, namely the restriction of the term "transition" to that material which exists between the primary and secondary themes. In the majority of works that I have analyzed there is typically a second transition between the secondary and closing themes, when these are clearly differentiated. This material often functions in the same manner as the transition between the primary and secondary themes, with the exception of its lack of modulation. In this sense, it acts just like the transition between the primary and secondary themes in the recapitulation. Thinking in terms of their melodic and harmonic function, P, S, C, and T take on the following qualities:
P, S, and C, are more tuneful and are harmonically stable. S may be at a lesser dynamic level and may be more thinly orchestrated. S and C are typically preceded by a cadence.
1T and 2T are less tuneful, are often represented by quicker notes, and are less harmonically stable. They are often at a greater dynamic level and are more thickly orchestrated. T typically ends with a cadence.
In order to present his melodic analysis in a format that he could use in conjunction with his graphic timelines, LaRue introduced a highly sophisticated symbolic language. As I have used his basic concepts essentially with undergraduates, and particularly for aural analysis, I have modified his language to fit my own particular needs. The following is my application of LaRue's symbols, taken in part from his lectures, and in part from his book (see Table I):
Table 1
LaRue's Symbolic Language
P primary material S secondary (contrasting) material C closing material T transitional material N new material (reserved for the development or coda) I introductory material (reserved for the slow introduction that may precede the allegro of sonata-allegro form) X a short motive that may appear at the opening of an exposition. When used, it typically permeates the movement's melodic material. (The four-note motive at the opening of Beethoven's fifth symphony, or the three-note motive at the opening of Brahms' second symphony are "X" motives.) V vamp 1P, 2S, 3T a number in front of a capital letter means "1st", "2nd", or "3rd", (i.e., 1P, 2S, 3T means: first primary material, second secondary material, or third transitional material). Pa, b, c a lower-case letter after a capital letter denotes a phrase, showing the smaller groups within the larger unit. Pa1, Pa2, Pa3 a variation of a phrase is shown by numbers. ex an extension of a phrase, too weak to be Pa1 or Pb, is shown as "ex". Pax, Pay, Paz a lower-case letter in superscript, following a phrase letter, denotes motives from that phrase. Sa[Pa] the main capital letters (P,S,C, and T) show their specific function. If S, C, or T are derived from earlier material, this may be shown by inserting the symbol for the earlier material (from which the later material is derived) in brackets and in superscript.4
Thus, 1Pb denotes the second phrase of the first primary theme; 2Sa denotes the first phrase of the second secondary theme; and 1Cc denotes the third phrase of the first closing theme. 1Sb[1Pa] denotes the second phrase of the first secondary theme, derived from the first phrase of the first primary theme.5
To apply LaRue's approach to an easily accessible composition, I have chosen the opening movement of Mozart's C Major Piano Sonata, K. 545. For the purpose of clarity, and to make my timelines accessible, I keep them as simple as possible. Therefore, the following analysis does not venture into the depths of analysis that LaRue's system ultimately allows.
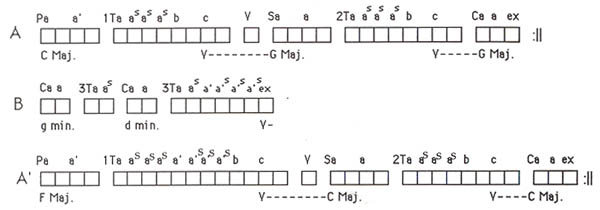
The movement is in sonata-allegro form, shown as a large-scale form of A-B-A'. Each measure is represented by a cube, thus the timeline represents visually the relative length of each section. For the purpose of clarity, spaces have been added between each middle ground idea. Melodic information is shown on top of the cubes; harmonic information is shown below. The symbol "s" has been used to indicate "sequence". (See Examples No. 2, a and b.)
Example No. 2a. Mozart: C Major Piano Sonata, K.545 (1st Movement), presented in a graphic timeline
Example No. 2b. Musical Examples. Mozart: Piano Sonata in C Major, K.545, 1st Movement.

This example is notorious for its recapitulation in the wrong key. It is also a clear example of the appearance of a second transition in the exposition, between the secondary and closing themes. The melodic function of the material between the secondary and closing themes is basically the same as that between the primary and secondary themes. The timeline shows the relative length of each large-scale section. In addition, it shows that the main difference between the recapitulation and the exposition, with the exception of harmony, is an added four bars to the first transition.
An Approach to Aural Analysis
In an attempt to help my classes hear a composition as it occurs in time, I began writing on the blackboard while the class was listening, and found that I naturally used LaRue's ideas, but with a twist. Rather than working with a graph, I began writing the numbers of phrase lengths down, and in time, a variation on LaRue's timeline began to appear. The following is a mock exposition of an early movement in sonata-allegro form based on my modifications of LaRue's system for aural analysis (see Example No. 3):
Example No. 3. A mock exposition of an early movement in sonata-allegro form with modifications for aural analysis.
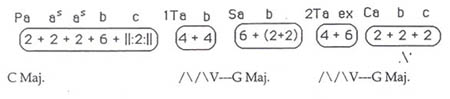
1. Each phrase (i.e., the middle ground: P, T, S, and C) is given its own separate unit.
2. LaRue's basic melodic symbols are used, with the addition of the following:
a) "as" is used to show "sequence." "Sequence" is used in its broadest sense, (i.e., meaning the same melodic material on any degree of the scale).
b) a repeat sign is used on each side of a number to show two or more measure repetitions. Octave displacement or a change in orchestration is ignored, as the repetition shows melodic function. If the repetition is fairly long and exact, except for one or two notes, it is also shown as a repetition, if that is its basic function. If the change is small but dramatic, then it is not shown as a repetition.
c) a repeat sign is used under a number to show a single measure's repetition. This is a more common occurrence than might be expected. (For an exceptional example, see bars 16-25 in the first movement of Beethoven's "Pastorale" symphony.)
3. Basic harmony is given below, with the addition of "/\/\/\" to show harmonic instability or modulation. The symbol "V—G Maj." is used to show cadences.
4. Numbers within parentheses show two sub-phrases that form a unit. As each individual number should have a symbol to show its function, this is especially useful when a larger phrase is more clearly shown divided, but the divisions do not warrant separate symbols.
The following example is the first movement of Mozart's C major piano sonata, K. 545, presented this time in an aural timeline (see Example No. 4).
Example No. 4. Mozart: C Major Piano Sonata, K. 545 (1st movement) presented in an aural timeline.

This is an excellent example to share with students because of its extreme familiarity and its clarity of form. As mentioned earlier, its one "flaw" is its presentation of the recapitulation in the wrong key. Nevertheless, I use this example frequently, since, with the exception of harmony, it defines the form extremely well. P, S, and C are each tuneful and harmonically stable; the transitions are non-tuneful and are harmonically unstable; the recapitulation is the same as the exposition with the exception of harmony and a four-bar extension of the first transition, not uncommon with Mozart. In addition, the movement includes clear examples of both sequence and repetition, and their functions become graphically apparent.
When presenting aural analysis, my class presentations take on the following format:
(1) I ask the class to determine the large-scale form of the movement, and determine the number of measures in each of the main sections. (This is usually done in one or two hearings.)
(2) I next ask the class to determine the lengths of the middle ground areas of the exposition (P, 1T, S, 2T, and C). (This may take several hearings, depending on the length and clarity of the work, and the ability of the class.)
(3) We next listen to each of the various middle ground sections to determine their subdivisions. (This may take any number of hearings.) It is important that the students hear the small repetitions and sequences that are so much a part of a typical classical composition. It is worth playing a phrase as many times as needed in order for the class to hear its various levels of complexity. (CDs make this activity relatively painless.)
(4) I next play the recapitulation to see what this may tell them about the exposition. (This may only take two or three hearings, depending on the clarity of the work and the ability of the class.)
(5) We next listen to the slow introduction or coda, if either exists. (The number of playings, again dependent upon the level of the students and the difficulty of the work.)
(6) We finally come to the development, which is usually the most difficult section for students to perceive. At this point I usually give them a hand-out with the main themes notated and labeled, so that they can both see and hear what is being developed.
If the work is comprehensive enough, I often have them figure out the exposition and recapitulation, and then I do the development on the board for them. Or I may present them with my own timeline at this point, and let them see while hearing how the development is put together.6
* * *
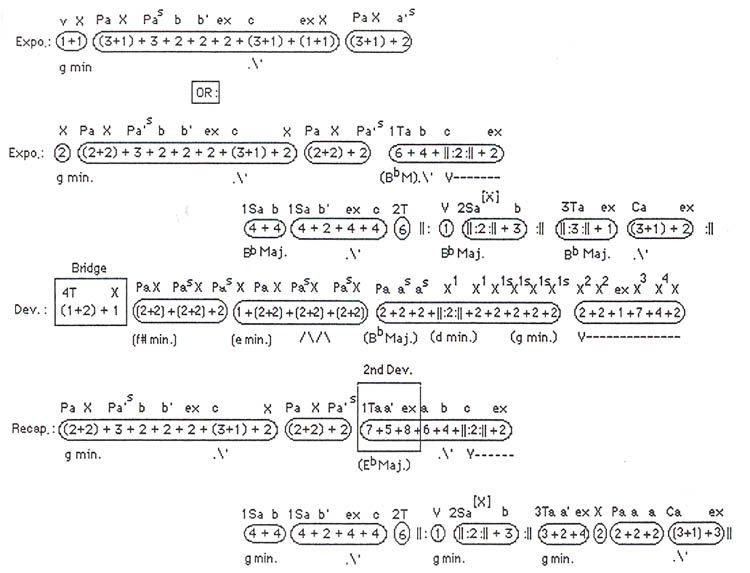
The next example is the opening movement of Mozart's Symphony No.40 in G Minor (see Examples No. 5, a and b).
Example No. 5a. Mozart: Symphony No. 40 in G Minor (1st Movement) presented in an aural timeline.
Example No. 5b. Musical Examples. Mozart Symphony No. 40, 1st Movement.

It is a good choice for the classroom, because it is so well known; it is also an especially intriguing example, due to its highly enigmatic phrase structure. Students and theorists alike hear its opening phrase in at least three different ways. Here are some possibilities: (see Table II).
Table II
Mozart's g minor symphony: opening phrase
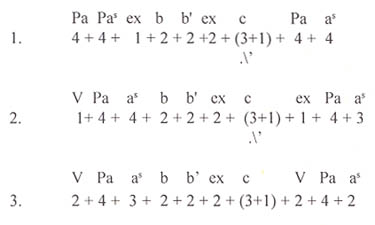
This example sheds an interesting light on the ongoing conflict between scholarly studies and practical performance. The performer (or conductor in this case) will put an accent at the beginning of the primary theme, depending on where he/she perceives it to be. Indeed, one of the problems of aural analysis is that we are at the mercy of the performance, which, as in the present case, could vary. Analysis can give us a certain kind of insight into the merits or deficiencies of both performers and conductors.7
Musical phrase structure is not always clear, and when ambiguous, it leaves room for personal interpretation. However, if studied long enough, and from as many angles as possible, a logical solution will usually emerge. This is the case with the opening of Mozart's 40th. If we pay attention to the harmony at the second statement of the primary theme, and again at the beginning of the recapitulation, it becomes clear that the primary theme does not begin until bar three of the opening (i.e., the harmony does not resolve to the tonic until this moment of the phrase in those other locations).
The thematic ambiguity in this symphony is perhaps what makes it ultimately so appealing. There are indeed several ways of looking at a work of this complexity. I have given two possible versions of the opening measures in Example 5a for the reader's contemplation. Although 1T starts out tuneful and harmonically stable in the relative major, it soon loses these qualities and turns into a clear transition. 2T also exhibits atypical behavior, but nevertheless does serve as a passageway between the first and second secondary themes. 2T could conceivably start eight bars earlier. Note that 2S is derived from X, but functions as a second secondary theme. What I have chosen to call 3T might also be considered part of the closing theme. There is a bridge between the exposition and development, typical of many examples in this form. As it does not really belong to either the exposition or the development, I have shown it in a box, to indicate that it stands alone. There is also an added 20 bars at the beginning of the first transition in the recapitulation. This acts somewhat like a second development section, typical of many of Mozart's works in this form. I have also shown it in a box, to draw attention to its special function. One of the more useful benefits of timeline analysis is the manner in which it makes a comparison between the exposition and the recapitulation so accessible.
It is clearly the lack of symmetry that makes the opening phrase of this movement so enigmatic. Philip Downs writes of these measures: "[They] demonstrate the subtle ways in which the composer makes his musical elements work against one another to create a feeling of tension and instability." "The resulting Affekt is one of unease, where one feels that something is wrong but cannot tell precisely what it is."8 For me, the feeling that something is wrong stems from the fact that, after a two-bar vamp, the opening phrase is asymmetrically structured (4 + 3) rather than (4 + 4).
And there is an important observation to make here. Although many works in the same genre will exhibit similar characteristics, and this is especially true of the less sophisticated examples, just as many works in the same genre will exhibit atypical characteristics, more true of the more sophisticated examples. LaRue himself warns us about trying to shove square pegs into round holes. He writes: "we must learn to regard each piece first as a unique expression and only later as a member of some general category . . . "9 Thus, it is important for us to teach our students that there are many musical compositions that conform to certain procedures that unite them in a particular class, but that within each class there is room for considerable variation and freedom.
* * *
The next example is the opening movement of Beethoven's third symphony, a work that demands considerable commitment on the part of the listener. I have included it to introduce the reader to a large-scale work, and to show that it is not all that difficult to comprehend the system, once one has taken the time to study it. Repeated listenings with the timeline will, I hope, present a rewarding experience. After looking at a fairly large number of works by Haydn, Mozart and Beethoven, Beethoven emerges as surprisingly "square" when compared to Haydn and Mozart. (See Example No. 6, a and b).
Example No. 6a. Beethoven: Symphony No. 3 (1st Movement) presented in an aural timeline.
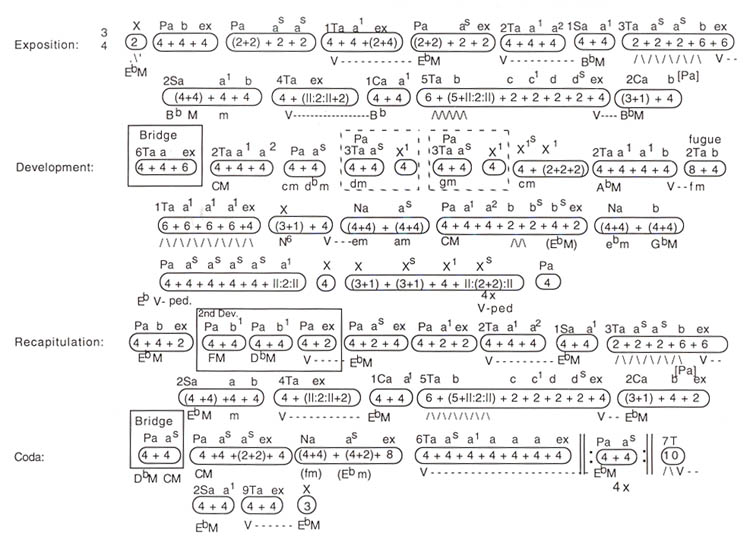
Example No. 6b. Musical Example. Beethoven: Symphony No. 3 (1st Movement).

Haydn and Mozart seem to be constantly experimenting with form, whereas Beethoven seems to be content to have learned from them, and moves ahead more by expansion. The third symphony is dominated by four-bar phrases, as are a great many of his works. The first movement features a main theme which is based on a simple triad, allowing the French horns to play it by using their natural overtone series. The transitions all act as passageways between the more stable melodic areas of P, 1S, 2S, 1C, and 2C, and four of the transitions are based on a dominant pedal. Note the 12-bar sequence in the development, shown by boxes. This idea will be expanded to a 46-bar sequence in the development section of the first movement of the sixth symphony. It is humbling to realize that Beethoven can get so much out of so little.
* * *
As mentioned earlier, I bring examples of vernacular music into my classes from time to time. I find the jazz quartet, in particular, especially useful for aural analysis. I begin by playing a few grounds by Purcell and some passacaglias and a chaconne by Bach. I then play a jazz version of a typical 12-bar blues and allow my students to see the close parallels between these Baroque and 20th-century forms. (I also remind them that Bach and Handel were well known as improvisers during their lifetime.) This activity never fails to win the approval of those students who already relate well to vernacular music, and it tends to gently shake up those who don't. Listening to jazz not only reinforces the same tools that we have been using with our classical examples, but it also helps to relax the class.
In closing, I would like to share my timeline for Dave Brubeck's "Blue Rondo à la Turk" (see Example No. 7).
Example No. 7. Brubeck: "Blue Rondo à la Turk" presented in an aural timeline.
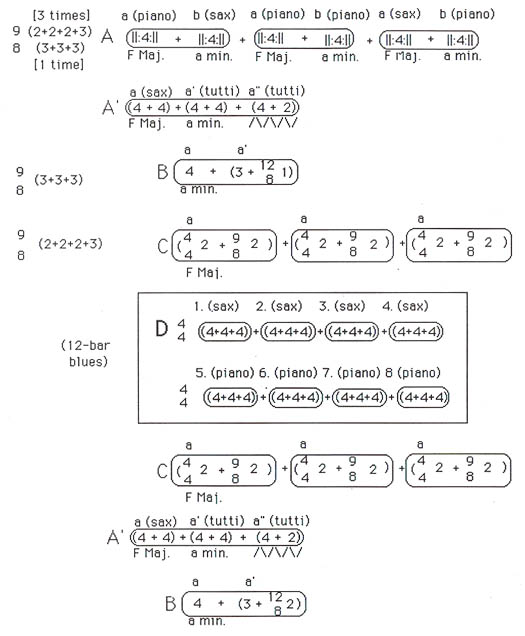
The work suffers slightly in its datedness, but is an excellent learning tool with its sophisticated yet accessible use of rhythm. The formal structure of the work is usually grasped by my students in three or four hearings. They also tend to enjoy Brubeck's use of musical devices, such as the opening motive appearing in augmentation in Variation Six of the section that is based on the 12-bar blues.
* * *
Each time that I return to earlier conceived timelines I continue to refine and reevaluate my earlier ideas. I am convinced that most readers will themselves find issues for debate within the present offering. My main point in writing this article has been to show a way of presenting aural analysis in the classroom using the basic tools made available by Jan LaRue. I am much less concerned about the manner in which each individual goes about using those tools and presenting his/her way of hearing individual compositions. Sometimes, on repeated hearings, music opens up to us in new ways, an important observation to make in the analysis classroom. (I heard Steve Reich's "Come Out" at least five times before I "heard" it.) It is useful for our students to understand that there are often options in the way in which we perceive things; this is especially true of the more sophisticated repertoire. Encouraging our students to look at things in more than one way, and from different perspectives, is perhaps one of the most important tools that we can give them.
1LaRue's approach to analysis can be reviewed in his book: Guidelines for Style Analysis (New York: W. W. Norton & Company, 1970), revised in 1992, published by Harmonie Park Press.
2LaRue made several changes from his lectures in the early 1960s when he published his book, Guidelines (1970), including changing "form" to "growth".
3J. W. N. Sullivan, Beethoven: His Spiritual Development (London, 1927), (published by The New American Library in New York, 1949).
4A more detailed and comprehensive discussion of LaRue's symbols may be found on pages 153-193 in either the 1970 or the 1992 edition of his text, Guidelines.
5Note: a melodic idea may be repeated, sequenced, or varied. Repetition and sequence are straightforward, but variation is often ambiguous. If the material that follows a melodic idea ("a") is different and significant, it should be labeled "b"; if the material that follows it is basically derived and significant, it should be labeled "a' "; if the material that follows it is basically insignificant, whether derived or not, it should be labeled "ex".
6I have been making my own timelines on Aldus Super Paint (3.5), a software program for the Macintosh computer that works surprisingly well for our purposes. Every two weeks I have my students prepare timelines of works not presented in class, but which act very similarly to those that have been presented. They are asked to prepare their assignments on Super Paint, and to facilitate this, our school provides a computer lab with at least 6-8 computers with Super Paint.
7For some interesting debates on the opening movement of Mozart's 40th, see the articles included in Mozart's Symphony in G, K. 550, edited by Nathan Broder and H. Robbins Landon, W. W. Norton Co. (1967).
8Philip Downs, Classical Music (W. W. Norton & Company, 1992), p. 520.
9LaRue, Guidelines (1970; 1992), p. 153.


