Philosophical, acoustical, and numerical considerations were not separate in the ancient world. They could be separated neither from each other nor from the overriding symbolism which informed and at times united them. It is difficult enough to embrace the idea of a synthesis of these channels of thought, but it is often virtually impossible to imagine the reality of the synthesis. Of the many specific difficulties that the twentieth-century mind encounters in attempting to understand ancient ideas, none is more confounding than the view of number and its two-fold nature in many of the civilizations whose ideas are known to us—including India, China, Babylon, and Egypt in the third and second millennia before Christ.
Number, geometry (literally, earth measurement), astronomy, and music were seen as four forms of a single concept of proportions both cosmological and actual with implications reaching into a gamut of concerns ranging from practicality to mysticism. The single concept may well have been one of what the ancient Chinese called "the four-fold things," but it was pervasive throughout the known ancient world: an interaction between two sets of opposing factors that forms a quadrivium of interrelationships. (The humors, for example, derived from the heat-cold, wet-dry oppositions.) The proportions were those of time and space, time equated with gesture and motion—considerations basic to metaphors of creation. This would become the quadrivium of the Liberal Arts.
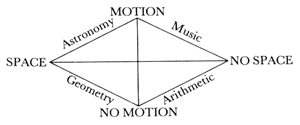
On the one hand, number was a practical tool; and with practical numbers the ancients were masters. A base ten was used in India by the fourth millennium B.C., a base twelve in Babylon, and both in Egypt, along with a base sixty for huge numbers. Cuneiform and hieroglyphic numbers were cumbersome in many relatively small computations, but they were capable of surprising economy in large ones—the Egyptians had a single symbol for one million and others for ten million and a hundred million.
On the other hand, number was aesthetic and speculative; we who are trained to manipulate numbers as servants in pursuit of practical problems find it difficult to conceive of enjoying numbers for their beauty and contemplating their symbolic properties without regard to practicality. And in fact the valued religious aspects of symbolic number led to the protection and preservation of symbolic numbers, while practical computations were given to sand, clay tablet, and abacus—preserved only in the works that they produced.
Perhaps the most puzzling to modern scholars is the use of different numbers for parallel symbolic and practical considerations—not the same numbers put to different uses, but different numbers, most significantly 3 and 3.1605, 12 and 13, 360 and 365. The Egyptian symbolic pi was 3, their practical pi was 3.1605; their symbolic circle of the year was of 360 days, but their practical year was the same as ours (and in meso-America's ancient calendar, more accurate still); ancient Chinese texts held that the body contained 360 veins but proposed 365 acupuncture points; an open circle was twelve, the closed circle was thirteen (a double concept that we have inherited in the "baker's dozen").
Modern mathematicians, finding the symbolic numbers and assuming their use in practical arithmetic, jumped at false conclusions about the ancients. Further, modern writers on the history of science have been impatient with the delight of the ancients in symbolic speculation, a delight which they did not understand and did not want to understand. Sarton, for example, questioned this love of the ancients for mere "fanciful ideas on the properties of numbers," which he termed "capriciousness" and a "luxury" he felt they could ill afford.1
It is time to look seriously at ancient symbolic number, and the musician has a special reason to do so, since music was central to the formulation of virtually all metaphors of creation—harmony was the working out of creative interactions of all types, and what we call music was an incorporation of its audible form.
Large numbers were intimately associated with cosmological speculation and symbolism; the numbers in the metaphors of creation in the 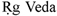 , for example, seem to have been at once geometrical and acoustical. Ernest G. McClain, in his study The Myth of Invariance, presents a succession of mandalas suggested by the ancient text, displaying them in geometric form and discussing their musical implications.2
, for example, seem to have been at once geometrical and acoustical. Ernest G. McClain, in his study The Myth of Invariance, presents a succession of mandalas suggested by the ancient text, displaying them in geometric form and discussing their musical implications.2
Practical music was the most accessible of the metaphors of creation, and it was the subject of highly sophisticated mathematical studies, whose practical applications may well have been of secondary importance. The relationship between theoretical and actual systems of pitch organization and of tuning is dimly understood even today.
All ancient civilizations seem to have been fascinated by the overtone series, the polarity between even and odd numbered partials, and in particular with the perfect fifth (for which the Egyptians had a special symbol), whose 3:2 ratio incorporated the male-female elements through which the cosmos had been created. The overtone series duplicates the pure series of numbers from one to infinity (itself a compelling polarity), while the partials as divisions (1, 1/2, 1/3, 1/4, etc.) form an infinite regress. The perfections of the sixth, eighth, ninth, and twelfth partials (6:8::9:12), audible, for example, as a-d'-e'-a', was a primary musical concept from the 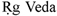 to Glareanus and beyond.
to Glareanus and beyond.
But the most vital proportion in ancient musical-mathematical speculation was that of the perfect fifth, and the idea of the circle of fifths seems to have been universal among ancient scholars. The practical circle, which Pythagoras brought back to Greece from his 22 years of study in Egypt, was of twelve fifths.3 But the full symbolic circle was of 360 fifths. How widespread the dual circle was is yet to be discovered, but it was known at least in Egypt and China, and most probably in Babylon as well.
My own realization of the extent of ancient arithmetical-musical concerns began twenty years ago when I read Curt Sachs's Rise of Music in the Ancient World, which incorporated a certain ambivalence toward ancient accomplishments in musical number. Particularly striking to me was the remarkable reaction of Sachs to the full symbolic circle of fifths, which he discussed in the chapter on China. That the great circle implied a computation of 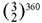 he found "grotesque."4 I was fascinated by the juxtaposition of his acknowledgment of so remarkable a concept and his dismissal of it.
he found "grotesque."4 I was fascinated by the juxtaposition of his acknowledgment of so remarkable a concept and his dismissal of it.
It seemed to me in 1976 that the full symbolic circle might not be "grotesque" and that I should examine it with respect. Clearly so huge a concept could have had no practical value, and in any case the creative function was fulfilled in the circle of twelve. Having no idea of the specific computations of the ancient Egyptians or Chinese, I figured the circle in modern terms, asking the Computer Center of the State University of New York at Binghamton for a print-out of 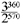 (rather than the
(rather than the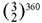 mentioned by Sachs, the lower number necessary to keep the lower tone within an octave of the upper one).5 The result was a fraction of two 172-digit numbers,6 which in this form is extremely cumbersome and, since the circle was not acoustically viable, probably irrelevant as well. More important was the ratio between these numbers: the upper is 1.501599692 of the lower.7 Thus in the steadily rising helix of untempered fifths, whether and however they computed it or contemplated it, the Egyptians and Chinese came full circle until the increments reached a perfect fifth in themselves.
mentioned by Sachs, the lower number necessary to keep the lower tone within an octave of the upper one).5 The result was a fraction of two 172-digit numbers,6 which in this form is extremely cumbersome and, since the circle was not acoustically viable, probably irrelevant as well. More important was the ratio between these numbers: the upper is 1.501599692 of the lower.7 Thus in the steadily rising helix of untempered fifths, whether and however they computed it or contemplated it, the Egyptians and Chinese came full circle until the increments reached a perfect fifth in themselves.
In cents the figuring is much simpler. The perfect fifth of 701.955 cents caused a sharpening of 1.955 cents for each degree of the circle (relative to the 700 cents of equal temperament). A circle of 360 fifths would mean a total increment of 703.8 cents, thus creating a comma of 1.845 cents (as versus 23.46 cents for the "Pythagorean" comma).8 That fifth, so high that it can belong only to the Music of the Spheres, seems a lovely capstone for a concept of great beauty. Certainly it is a glowing tribute to the ancients as remarkable and imaginative people.
1George Sarton, Study of the History of Mathematics (New York, 1957), p. 18.
2Ernest G. McClain, The Myth of Invariance: The Origin of the Gods, Mathematics and Music from the 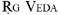 to Plato (New York: Nicholas Hays, Ltd., 1976). The numbers discussed by McClain include the cycle of 155,520,000,000,000 years in the
to Plato (New York: Nicholas Hays, Ltd., 1976). The numbers discussed by McClain include the cycle of 155,520,000,000,000 years in the 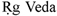 ; he finds 1,555,200,000,000 as "one year of Brahm
; he finds 1,555,200,000,000 as "one year of Brahm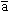 ," and the full 155 trillion as "the life of Brahm
," and the full 155 trillion as "the life of Brahm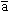 ," saying that he "cannot find this number in the
," saying that he "cannot find this number in the 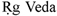 , but several passages can be read as allusions to its yantra" (p. 89). The number 360 was crucial in computing the "year," which was a religious year of 360 days. Some of the same figures appear in Babylonian calculations (p. 136).
, but several passages can be read as allusions to its yantra" (p. 89). The number 360 was crucial in computing the "year," which was a religious year of 360 days. Some of the same figures appear in Babylonian calculations (p. 136).
3The circle of twelve fifths was an "open circle," ending not with return to the enharmonic octave (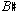 if beginning on C) but on
if beginning on C) but on 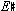 . In their terms, the modern circle, which begins and ends on C (C to
. In their terms, the modern circle, which begins and ends on C (C to 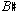 ) is a closed circle of thirteen and hence uncreative. The creative value of the number twelve was doubtless ancient when the School of Music known to Pythagoras had been founded in Thebes in the Middle Kingdom (about 1,300 years before Pythagoras was there), and it continued through Renaissance times. In an article on number symbolism in the sixteenth century (as Preface to his edition of the anonymous Mass of Breslau MS #2016 [Das Chorwerk #56]), Fritz Feldmann calls the number twelve the Schöpfungszahl; his analysis of the phrase lengths (in maxima) in terms of the symbolism of number is thorough and persuasive.
) is a closed circle of thirteen and hence uncreative. The creative value of the number twelve was doubtless ancient when the School of Music known to Pythagoras had been founded in Thebes in the Middle Kingdom (about 1,300 years before Pythagoras was there), and it continued through Renaissance times. In an article on number symbolism in the sixteenth century (as Preface to his edition of the anonymous Mass of Breslau MS #2016 [Das Chorwerk #56]), Fritz Feldmann calls the number twelve the Schöpfungszahl; his analysis of the phrase lengths (in maxima) in terms of the symbolism of number is thorough and persuasive.
4Curt Sachs, The Rise of Music in the Ancient World (New York, 1943), p. 117.
5This process is necessary in all commas; in the syntonic comma, for example,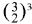 or
or 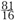 is corrected to
is corrected to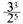 to arrive at
to arrive at 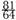 ; this then gives a major third instead of two octaves plus a major third.
; this then gives a major third instead of two octaves plus a major third.
63360 = 5,802,988,355,301,064,263,572,941,269,018,812,264,886,757,498,342,118,039,827,
603,956,893,368,389,206,154,994,705,426,429,662,904,979,537,365,662,938,773,
593,537,918,329,060,451,697,709,838,267,789,886,857,631,025,156,060,199,201.
2570 = 3,864,537,523,017,258,344,695,351,890,931,987,344,298,927,329,706,434,998,657,
235,251,451,519,142,289,560,424,536,193,766,581,922,577,962,463,616,031,502,
177,177,365,078,661,042,987,655,742,908,673,467,080,748,696,980,814,823,424.
Special thanks are due to Burton Avery of the Computer Center and to Joseph Kotylo, Administrative Assistant to the Chairman, Department of Music.
7The ratio was provided to me by Alan R. Fisher, Design Engineer, Advanced Transmission Department of the Ford Motor Company, Livonia, Michigan. I am indebted to Mr. Fisher not only for his kindness but also for his appreciation of the implications of my questions.
8Those interested in detailed calculations in cents are referred to Fred Lieberman's excellent article, "Working With Cents: A Survey," Ethnomusicology, XV, 2 (May, 1971), pp. 236-242.


