Since the present discussion deals with music, and since music deals with number as it relates to sound, mathematics must be discussed first.1 . . . . . Walter Odington, ca 1340
Definitions of musicology usually make reference to the use of scientific methods that the discipline, whatever its focus, must use. An examination of the criteria used to achieve a scientific method is seldom the concern of such definitions, but it is vital to the musicologist. The criteria, or the design of analytic procedures that purport to incorporate a scientific approach to the subject under study, are well known to most practitioners of historical musicology. They were developed from methods first set down by the German historian Leopold von Ranke (1795-1886). Ranke's major works are primarily histories of ideas in the Hegelian sense: concepts built upon facts that serve to verify the cogency of the concepts. A fact for Ranke is "wie es eigentlich gewesen," as it actually happened.2 Ranke strives for a scientific historiography after the investigative procedures of the physical sciences where facts are commonly seen as empirical phenomena that can be measured, classified and documented as they occur.
Music theory, as it is considered under the aegis of musicology, also strives for scientific method in the formulation of analytic procedures. As such, it is subject to the same criteria of examination and reformulation as the physical sciences. An analytic procedure may be considered successful if it provides useful insights into the organization and structure of works of a given musical style. An evaluation of an analytic procedure from the standpoint of scientific efficacy would appear to take two possible paths. The first would be concerned with the flexibility of the analytic procedure to deal with minor stylistic vagaries. Such vagaries may not so much prove the rule as they may be indication of stylistic changes the analytic procedure is not designed to explain. The second path, and the concern of this paper, has to do with evaluation of analytic procedures from the standpoint of scientific design.
The quantitative analysis of music includes several methods that attempt to answer questions about musical structure in precise, measurable terms. They have, to date, not gained much acceptance. The reasons for this are attributable in part to design flaws. Few will quarrel with the generally perceived advantages of scientific objectivity in discussing physical phenomena. Scientific procedures have been attractive to many music theorists, yet the kind of empirical testing that characterizes standard laboratory methods in the physical sciences has been slow to take hold in the design of analytic procedures in quantitative analysis.
Efforts in the quantitative analysis of music have reached print during the past two decades. The first appeared in Germany and have not been many in number. These papers deal with methods of measuring pitch, interval and/or duration as separable compositional elements. Jack Watson is credited with providing the first definition of quantitative musicological research as "the application of statistical procedures to studies of musical phenomena involving information theory."3 The definition of statistics that has to do with the assembling, classification and tabulation of numerical data is consistent with Watson's definition and the analytic procedures used in these papers. The application of information theory by these authors is relevant, but varies. Information theory is a scientific discipline concerned with defining the "quantity of information in a message to be transmitted."4 In information theory a musical score may be seen as a system of symbols in the form of musical notation which, when perceived (read by or performed for those familiar with the musical style), becomes information transmitted from composer to listener. Four of the five papers discussed here contain original methods of quantitative analysis. Each method is described, then examined for its faithfulness to scientific procedures and for its philosophical implications.
Léon Brillouin cites two distinct methods of scientific inquiry: "In mathematics, definitions start with a certain number of carefully selected and stated postulates, and the more complex entities are derived, and defined in terms of these initial postulates. Experimental sciences have introduced another type of definition, often called 'operational.' Force, mass, velocity, etc., are defined by a short description of the type of experiment required for the measurement of these quantities."5 The purpose of such careful exegesis, whether a mathematical process, an operational procedure, or a combination of both is involved, is to provide adequate information to make it possible to test the theory by replication of the experiment.
Wilhelm Fucks uses statistical tools to measure pitch, duration and intervallic relationships taken from the first violin parts of fourteen symphonic works from the Baroque, Classic, Romantic and Contemporary eras in his paper of 1957.6 The works chosen favor the Classic era: two Baroque, six Classic (five of which are Beethoven symphonies), five Romantic and one modern work. The soprano parts of eight choral works are also examined. They favor the contemporary era: two Gregorian masses, one Renaissance mass, one Romantic and four modern masses (three of which are by Arthur Meulemans, 1884-1966).
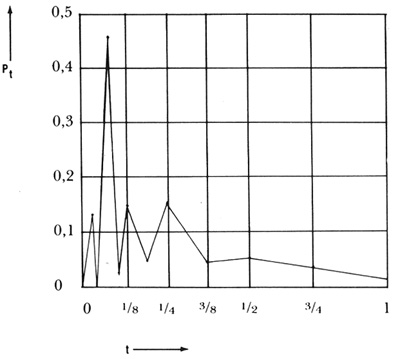
Three compositional elements are tabulated for each note: duration, pitch and intervallic relationship. The formulas are given that allow the generation of statistical findings on the first violin or soprano parts of the twenty-two works examined. Graphic representations are given for the frequency distributions for each compositional element, the first of which are for durational values (Ex. 1).
Ex. 1. Fucks' summary of pitch frequency (Pt) and durational value (t) for the first violin part of Strauss' Tod und Verklärung.
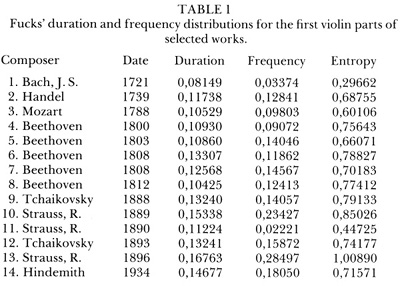
Distributions are then summarized for all the violin and soprano parts for duration, frequency and entropy (Table 1).7
Intervals are also subjected to the same statistical analysis and presented in similar format. Tables are given that compare the works by style period for frequency distribution of pitch, duration and interval. Sample tabulations are included. Fucks closes his paper with an excerpt of stochastic music analyzed for pitch and interval distribution. The composition was written with the help of a roulette wheel.
Fritz Winckel takes a wide-ranging approach to quantitative analysis through a discussion of information theory.8 He characterizes it as a field of semiotics, the study of signs. Winckel surveys Fucks' statistical procedures, using it to analyze the first violin parts of Beethoven's String Quartet, Op. 74, and Webern's String Trio, Op. 20, for pitch, duration and intervallic relationships. Winckel's findings are presented in the same graphic format as that used by Fucks. The remainder of Winckel's paper speculates on the role of the concept of redundancy in statistical analysis, aesthetics in the creative process, the role of new music, the concept of communication in art, and finally, a brief discussion of the role of information theory in describing aspects of the aesthetic experience.9
Hans-Heinz Draeger also summarizes Fucks' analytic procedure.10 Draeger differentiates between tonal orientation and tonal organization. He defines tonal orientation as "the over-all tonality in a given sequence without consideration of the temporal order of the tonal events." Tonal orientation "is revealed by the statistically important notes in any given piece or movement." Tonal organization "means the tonal structure of a given sequence with consideration of the temporal order of tonal events." Draeger's use of the term sequence is not defined, but he continues by saying that tonal orientation is to be determined statistically and may show important pitches in a composition that may be significant in the work's tonal organization. "A piece in C major, for example, may be oriented toward G major or F minor, and this tendency towards another key has considerable semantic significance." Draeger predicts a significant area for future research in the quantitative analysis of the relationships between tonal orientation and tonal organization of bodies of stylistically related works. He cites a master's thesis by Matt Hughes as an example of such work.11
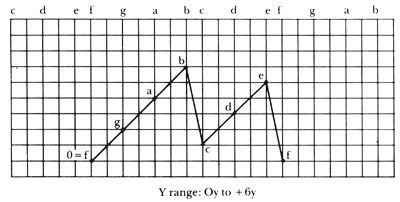
Draeger also summarizes work done by Yehoshua Lakner as an example of quantitative analysis.12 Lakner's procedure employs graphic representation of intervallic relationships on intersecting axes, one melodic (size of the interval) and one harmonic (denoting the ratio of the two pitches). Lakner demonstrates the interdependence of the two factors, calling his procedure graphic analysis. Lakner's theory of tonal organization based on the circle of fifths parallels Draeger's construct. Both writers cite Pythagoras' speculations to support their determination of intervallic direction for tonal relationships based on the circle of fifths. Both writers imply modes of perception of tonal direction from their systems that are suggestive of the ancient doctrine of the affects. Lakner: "The psychological effect of the mode thus depends on the position of all the other tones of the mode in relation to the root; in the degree to which they are plus y (ascending) or minus y (descending points on the harmonic axis) in relation to it. Thus, in the Lydian mode, all tones appear as ascending fifths (plus y) in relation to its root—like a mountain arising before the listener" (Ex. 2).
Ex. 2. Lakner's graphic representation of pitch relationships for the Lydian mode.
Draeger: "From Josquin on, the tonal movement up and down in the circle of fifths has been associated with emotional contents. . . . The only valid characterization, from a psychological point of view, remains therefore 'up' and 'down'."
Draeger rejects a simple assignment of numerical values to each pitch, arranged by fifths, as unproductive. He had earlier developed this method of weighing tonal pitches, following Lakner, and reported in his paper at the 1964 symposium in Salzburg.13 Draeger uses a graphic representation of pitch movement for the present paper providing analyses of the last two measures of three of Beethoven's thirteen sketches for the fourth movement of his String Quartet, Op. 131. He picks the three sketches that are closest to the final version for analysis, the fourth, the sixth, and the final version. Example 3 provides Draeger's excerpt of Beethoven's fourth sketch of the last two measures of the fourth movement and the graphic analysis he derives from it.
Ex. 3. Beethoven's fourth sketch for the last two measures of his Op. 131 (fourth movement) and Draeger's graphic analysis.
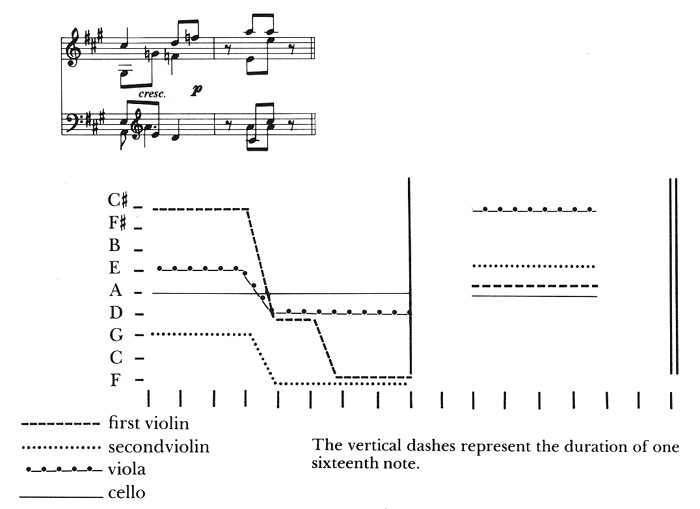
Duration is measured by sixteenth notes represented by the vertical lines along the bottom of the graph. The graphic representation of these two measures shows a "downward tonal movement" that Draeger characterizes as in "balance [with] the upward tonal movement of the individual voices towards the final chord [that] is good."
Matt Hughes' paper, "A Quantitative Analysis," is part of a published symposium of analyses of Schubert's Moments Musicáux, Op. 94, No. 1.14 In it, Hughes borrows Draeger's procedure of counting durational values and elements of Winckel's Redundanzbegriff in the design of his analysis. It is presented in a useful step-by-step manner that provides tabulations and a statistical summary for each section of Schubert's Op. 94, No. 1 (Ex. 4).
Ex. 4. Hughes' graph showing tonal complexity in mm. 1-8 of Schubert's Op. 94, No. 1, by percentage.
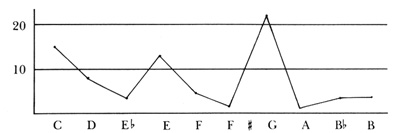
Hughes also provides a similar summary for the composition as a whole. This allows one to compare tonal complexity section by section with the piece as a whole. Other compositional elements that may be so compared are tonal orientation (step 2); tonal "events" (after Draeger), tabulated according to the circle of fifths (step 3); computation of note number averages to identify the "location of the composition as shown by the circle of fifths" (step 4); isolation of the significant tonalities, both by occurrence and distance relationships (step 5); and identifying the differences between the final totals of step 3 and 5 (step 6). Hughes also uses Draeger's graphic analysis of cadence formulas in his study, echoing Draeger's interpretation of the ascending movement of tonalities in the circle of fifths as an "open, non-final effect" and descending movement as motion toward a close.
Each of these methods of quantitative analysis has speculative aspects that expose two areas of concern for this writer, one procedural and one philosophical. The procedural problems have to do with the operational definitions each writer uses. The mathematical aspects of each procedure are reasonably clear and verifiable. The operational definitions are of concern, however, since they are sometimes poorly stated, confusing speculation with fact.
Operational definitions in Fucks' article are largely absent. His statistical procedure is summarized as too elementary to provide significant musical data by several of the participants in the round table of the 1964 meeting in Salzburg or the International Musicological Society.15 The samplings assume that there is a correspondence between the tonal, durational and intervallic characteristics of the first violin and soprano parts and the works as a whole in which they are found. Fucks gives no justification for this assumption. The elements measured are tabulated as totals for the entire works, without consideration for tonal relationships or their structural roles. Finally, the basis for selection of the compositions chosen is not given.
Winckel summarizes Fucks' work and surveys information theory, speculating on its relevance to quantitative analysis and the aesthetics of music. Since Winckel adopts Fucks' methods of quantitative analysis without alteration, the above criticisms are applicable here.
Lakner's graphic analysis appears to be based on sound mathematical procedures and postulates. Operational definitions are less satisfactory. His graphic analysis is based on the plotting of two coordinates, x, the melodic factor, and y, the harmonic factor. The graph is divided into twelve equal parts to represent the chromatic scale. Movement to the right, plus x, represents melodic ascent; movement to the left, minus x, represents melodic descent. Lakner characterizes harmonic movement as inseparable from melodic movement, presupposing the Westerner's musical orientation. "The factor y determines the size of the factor x." It is found with this method that the positions of x and y produce parallel coordinates for the perfect fifth while coordinates for x and y of the perfect fourth are plotted in the opposite direction. Lakner considers this a confirmation for ". . . the well-known feeling that the root of the fifth is its lower tone . . . yet, on the other side, we feel that the root of the perfect fourth is on top, as if stood on its head—and we ascend to its root." On harmonic direction: ". . . factor y, therefore, is measured by the number of perfect fifths necessary to extend from one tone to another, without regard to the octave in which they appear." Each of the graphic analyses of the modes (Ex. 2) makes use of diminished fifths, treating them as if they were perfect, however.
Lakner is less than persuasive when he justifies the use of a fifth-oriented system of analysis on the basis of an apparent happenstance of statistical procedure. An unsubstantiated assertion about how people perceive perfect fourths and fifths is not supportable evidence. Pythagoras' experiments are relevant to the tuning of scales, but their relevance to Lakner's graphic representation of melodic and harmonic movement is not demonstrated. His use of the terms "harmonic height" and "tonal space" is metaphorically suggestive but only that when they are used without definitions.
Draeger's graphic analysis has the virtue of simplicity of construction. It is based on a fifth-oriented analysis of tonal relationships after Lakner, whom he cites in detail. Such precedents are not adequate to take the place of operational definitions, however. Also, Draeger's use of "tonal orientation" and "tonal organization" to differentiate between the overall tonal structure of a work and the temporary tonal changes that articulate the structure remain unconvincing. He uses the word "sequence" in the definitions for each to refer to a variety of structural components without ever defining his special use of the word. "[Tonal orientation] means the overall tonality in a given sequence without consideration of the temporal order of the tonal events; [tonal organization] means the tonal structure of a given sequence with consideration of the temporal order of tonal events. In other words, the overall tonality—tonal orientation—is revealed by the statistically important notes in a given piece or movement." Finally, Draeger's graphic representation (Ex. 3) does not easily lend itself to extended excerpts. It is too cumbersome for more than brief passages, preferably cadences, where tonal movement usually reinforces tonicity.
Hughes' presentation is the more accessible of the papers discussed here. His mathematical postulates are clear and presented in detail. His operational definitions, based on Draeger's constructs, suffer from the same defects as his predecessor's presentation, however. Like Draeger, he avoids dealing with pitches as elements of scales by using the Pythagorean experiments as justification for his construct. All pitches are related through the circle of fifths and assigned numerical values from 1 to 25 for all pitch spellings, from D-double flat to B-sharp (step 3a). His justification for this procedure falls short of an operational definition: "Because we are dealing entirely with underlying tonal orientation and have the problem of reducing it to as simple a structure as possible, it is quite logical to contend that further insight might be achieved when given an equally simple structure. The circle of fifths, as a basic tool, fulfills this essential requirement for simplicity and this procedure offers a possible solution." The relevancy of the circle of fifths to the role of scalar pitches in determining tonality is not demonstrated nor is the validity of an arbitrary assignment of numerical values to these pitches to tonal structure shown.
The observations made at the 1964 conference in Salzburg with reference to Fucks' procedure would also appear to be applicable to Hughes' procedure. As Hughes indicates, "Analysis of tonal organization is an analysis of chords, progressions, measures, and periods in their mutual relationships. [Tonal] orientation . . . is a result of the total occurrence of each note and its durational value." His procedure fails, however, to relate each pitch to its tonal context within each measure so that the tonal relationships that articulate the musical structure can be verified. All pitches are instead related to their assumed functions as members of the circle of fifths.
A recurrent philosophical concern that appears when scientific methods are discussed in attempting to understand a work of art is how one is to protect the ineffable qualities of the aesthetic experience or the creative process. Many composers recognize this concern in identifying the finished composition as a separate entity, sometimes metaphorically, as one of their children, who have their own lives to live once completed. The anthropologist uses the word "artifact" to identify such works. The differentiation between the art of creating a musical work, or the art of its performance, or the aesthetic experience one can have from the performance is a vital one. The music under consideration here becomes an artifact once it becomes a score. Our examination of this artifact can meet the specifications of scientific procedure if our analytic techniques are to be productive. We can deal scientifically with the quantitative aspects of the compositional elements of music in artifact form, but the appraisal of modes of perception has yet to produce the kind of standardized instruments that allow meaningful results. The criticism which has befallen the Stanford Binet test in recent years reflects this problem. Of the writers discussed here, only Fucks touches on the problem of differentiating between the creative and aesthetic aspects of music and the artifact by which it is symbolically represented. "We think of a score as a given concrete example, fixed in performance, every single note of which is apprehended as an element by the eye." Fucks designs his analytic procedure for the score, however, without taking into consideration that he is including performance practice styles in his focus when he adds parenthetically, "fixed in performance." He has thereby unnecessarily blurred the philosophical focus of his study, since his procedure deals only with the measurement of pitch, duration and interval as represented in the score. If Fucks were to design an analytic procedure concerned with the performance his artifact would probably be the recording, not the score.
Winckel is provocative in discussing the directions in which technology may go in exploring the cognitive processes involved in the aesthetic experience. But the scientific procedures that will move these concerns from speculation to fact are not approached. Since Winckel's article is a summarization of others' research, there is no philosophical position pursuant to original research to examine.
Draeger's rationale for devising a method of ascribing numerical values to all the pitches of the tempered scale in a fifth-related series after Lakner is based on speculation that does not achieve the operational definition of scientific procedure. Draeger says of his conversion table, "The validity of the mathematical definition [which definition he does not specify] is obvious, and this evidence may shed some light on the question of whether or not there are neurological reasons for the association of mathematical data with human emotions." Draeger appears to be suggesting that the justification for a tabulation of pitches based on the circle of fifths will someday be verified by psychological research into the emotional responses of the aesthetic experience in music. Until science has the technology to verify that man hears tonal relationships through a series of ascending or descending perfect fifths and that such "tonal" movement is the basis for aesthetic responses, we have two options: we can accept the theory on faith, or we can reject it as unsubstantiated. Draeger describes no experiments that might demonstrate the validity of his theory.
Hughes, like Draeger, avoids dealing with pitches as elements of scales by using the circle of fifths construct. His justification for adopting this procedure also falls short of an operational definition. The relevancy of the circle of fifths to the compositional role of the scale degrees is not demonstrated by the differentiation between tonal organization and tonal orientation unless the relationship between each transient tonality and the structurally significant key it articulates can be identified and quantified. The argument by analogy is not adequately demonstrated by "equally simple structure" (see quotation, above).
Watson's definition of quantitative musicological research (see above) has the simplicity of all good definitions in that it names the elements that distinguish quantitative research from other analytic techniques. These elements are statistics and information theory (now more commonly known as information science). The procedures discussed here vary in the use of these tools. Fucks and Lakner employ statistical tools. Draeger emphasizes information theory in describing his statistical applications. Hughes identifies only statistics as his extra-musical discipline, but his principal concepts and operations are borrowed from Draeger. Fucks' approach to quantitative analysis deals with individual tonal pitches as if their only significance is as members of pitch aggregates in the entire composition, ignoring all tonal relationships that define structure. Draeger takes an opposing view when he says that his analytic procedure "is dealing with individual and discrete entities, with events that happen on particular occasions indeed with very minute details." The graphic analysis that results, however, is too cumbersome for extended analysis.
Finally, the circle of fifths construct that Draeger and Hughes derive from Lakner's analytic procedure ignores one of the composer's primal compositional tools, the scale. An analytic procedure that attempts to allow the musical phenomena to suggest the design of the analytic model, not the reverse, must take into consideration all relevant compositional elements. The role of the scale in articulating tonicity was first described by Fétis over one hundred years ago.16 Lakner, Draeger and Hughes avoid dealing with tonicity in the design of their analytic procedures by using a circle-of-fifths-oriented construct as the basis for their procedures that is operationally ill-defined. The samplings are too limited, also, to provide enough results to make quantified statements about tonal phenomena beyond the brief musical excerpts analyzed, although Draeger and Hughes imply a positive correlation of tonal characteristics between the samplings and the works in which they are found. Draeger, following Fucks, implies similar correlations with other works of the same style periods. Such presumed correlations must remain speculative until analytic techniques are employed that meet the criteria of scientific procedure and provide surveys that are broad enough to support quantified comparisons.
There is an increasingly widely felt need in music theory for the dispassionate and objective approach to the understanding of music that quantitative analysis can provide. The men whose work in this direction that has been discussed here deserve praise for their efforts. They have taken the first steps toward the development of a discipline that holds out the promise of making possible for the first time precisely quantified statements about the compositional elements of music that can give the composer much greater control over his musical resources and the listener greater insight into his aesthetic experiences. Martha MacLean Hyde has shown (in this publication and elsewhere) how Schoenberg used a quantitative approach to durational values to organize the structure of his String Trio, Op. 45 (1946).17 If a composer has already done it, can the theorist be far behind?
1Corpus Scriptorum de Musica, ed. Frederick Hammond; 14, 44. Cited by Richard J. Wingell in "Anonymous XI and Questions of Terminology in Theoretical Writings of The Middle Ages and Renaissance," Music Theory Spectrum 1 (1979), 125.
2Leopold von Ranke, Geschichte der Romanischen und Germanischen Völker, preface to the first edition; Werke (Leipzig, 1874) 33-34, vii.
3"Analysis and Synthesis of Musical Structures on The Basis of Information Theory," Kongressberichte, Salzburg, 1964, 2 (1966), 261-268.
4Lejaren Hiller and Leonard M. Isaacson, Experimental Music: Composition with Electronic Computer (New York: McGraw-Hill, 1959), p. 22.
5Léon Brillouin, Science and Information Theory, rev. ed. (New York: Academic Press, 1962), x.
6Wilhelm Fucks, "Mathematische Analyse der Formelstruktur von Musik," Forschungs-berichte des Wirtschafts- und Verkehrsministeriums Nordrhein-Westfalen, No. 357 (1957), 1-46.
7John R. Pierce, in his seminal book An Introduction to Information Theory (second revised edition), provides the following definition of entropy: "The entropy of communication theory, measured in binary digits (bits) per symbol or per second is . . . the average number of bits per symbol or per second which are needed in order to transmit messages produced by the source. [It] . . . is interpreted as average uncertainty as to what symbol the source will produce next or the average choice the source has as to what symbol it will produce next."
8Fritz Winckel, "Die Informationstheorietische Analyse musikalischer Strukturen," Die Musikforschung 17 (January-March, 1964), 1-14.
9For a speculative and useful approach to the relevance of information theory to the aesthetic experience, see Leonard B. Meyer, "Meaning in Music and Information Theory," Journal of Aesthetics and Art Criticism 15 (1957), 412-424.
10Hans-Heinz Draeger, "Quantitative Analysis of Music as Exemplified by Beethoven's Sketches for His Opus 131," Festschrift für Walter Wiora, ed. Finscher and Mahling (Kassel: Bärenreiter, 1967), pp. 79-85.
11Matt C. Hughes, "Tonal Orientation in Skriabins Preludes" (unpublished master's thesis, Austin, University of Texas, 1965).
12Yehoshua Lakner, "A New Method of Representing Tonal Relations," Journal of Music Theory 4 (1960), 194-209.
13Hans-Heinz Draeger, "An Attempt towards a Semantics of Chordal Progressions," abstracted in "Analysis and Synthesis of Musical Structures on the Basis of Information Theory" (see fn. 3 above).
14Matt C. Hughes, "A Quantitative Analysis," Readings in Schenker Analysis and Other Approaches, ed. Yeston (New Haven: Yale University Press, 1977), pp. 144-164.
15Ibid., 264-266.
16François-Joseph Fétis, Traité complet de la théorie et de la pratique de l'harmonie, eleventh ed. (Paris: Brandus, 1875).
17Martha MacLean Hyde, "The Roots of Form in Schoenberg's Sketches and the Teaching of Atonal Theory," College Music Symposium 20 (Fall, 1980), 130-137.


