What passes today in many textbooks and classrooms as harmonic analysis is the result of a misconception, historically understandable but pedagogically barren. At the root of the misconception lies the confusion—or at least fusion—of thorough—bass practice and harmonic theory. We shall follow the harmful implications of this want of distinction and then outline the advantages of a necessary separation.
Figured bass is a shorthand notation and nothing more. It offers no explanations of musical behavior. It describes a chord with numbers rather than notes but reveals nothing of its nature or function that could not be directly read off the musical notation. As a stenographic device, it saves time but cannot possibly produce fresh insights. For more than two centuries, harmony instruction was identical with thoroughbass realization. The goal was exclusively practical. One learned a technique, not a theory, of connecting chords with each other. The few rules involved—addressing themselves to doubling of tones and avoiding of certain parallel progressions—all were concerned with proper sonorities bringing about practical effects. Theoretic questions were neither asked nor answered. The harpsichord player did not care whether a chord struck by him was a tonic or a dominant as long as he hit the notes prescribed by the figures. The value of this kind of instruction was great but limited. It prepared musicians to become proficient performers and, in the case of aspiring composers, to spell correctly. But neither keyboard fluency nor orthography has any connection with theory, let alone with analysis. They are mechanical tools which by themselves offer no insights into musical drives and behavior.
Analysis of a musical composition is characteristically a modern concern which began to unfold in the middle of the nineteenth century. In the whole earlier literature of music theory, there is barely a passage that tries to analyze or explain a musical phrase. The medieval writers deal either with practical innovations, such as notation, or theoretic norms, such as consonances, but they do not try to tell the reader what to listen for in a piece of music. With the new attention to expression and communication around the year 1600, writers do indeed quote specific passages from compositions in order to illustrate a general point. In the fourth and last part of the Istitutioni harmoniche, Zarlino refers to various works but primarily in order to advise composers on what modes to use for what effects. The several famous forewords by Monteverdi, to give another example, are closer to modern concerns. Still these writers, whom we may credit with being forerunners of analysis, are less interested in explaining how things had happened than with demonstrating how things may be done—in short, again practical rather than theoretic in their approach.
In the middle of the nineteenth century, the musical atmosphere changed drastically. The reason lay in the widening distance between composers and listeners, intensified by both sides. Composers, true representatives of the romantic spirit, became increasingly subjective in their expressions and productions and thus ever more in need of being "explained" to the listeners. Whereas earlier composers—Bach, Haydn, Mozart—never gave a thought to interpreting their music in words to their audience but took it for granted that the music spoke for itself, Schumann, Berlioz, and Wagner matched their musical output with their prose writings. Schumann founded the Neue Zeitschrift für Musik mainly in order to bridge the developing gap between composers and listeners. The latter, for their part, found themselves further away from new music than ever, for their sociological makeup had changed. No longer were they a small, well-defined elite, often the composer's employers and friends, and almost always educated Liebhaber, amateurs, lovers, of music. Rather the audience was now a heterogeneous, ever-growing mass of relatively uninformed newcomers who needed help. Compositions, for the first time in history, had to be explained and analyzed for them; and a whole new translation of music into words came into being. Terms like sonata form, development section, and the like were not known to Beethoven. They were invented around the middle of the century by critics and teachers forced to talk about musical issues. It is reported that when Beethoven was once asked to explain one of his new compositions to a sympathetically inquiring lady, he responded by sitting down and playing it again. The generation after him instead required program notes.
While thoroughbass instruction lingered on, the new verbalization of musical experiences led at its best to real and valuable theoretic insights. A main characteristic of true theory is the absence of any instruction on "how to do" things. Theory tries to recognize the forces active beyond the surface of a composition. It inquires into "why" and not into "how." In this sense, original music theorists have been few and far between: Plato and Aristotle but not Boethius; Jacob of Liège but not Grocheo; Zarlino, Rameau, Riemann, but not their commentators and compilers. Over the centuries, the particular issues of theory have, of course, changed. The Greeks faced the challenge of setting up systems. At the time of early polyphony, consonance and dissonance relationships had to be clarified. With triadic homophony establishing itself, the nature and functioning of chords moved into the center of attention. Today the theory of harmony (as distinct from the theory of forms or of hearing or of new systems) remains indebted to Rameau, but we know from history that a span of two to three hundred years is generally part of one wave. The central task of harmonic theory underlying harmonic analysis is to understand why chords are what they are and why they behave as they do.
With this distinction in mind, one must readily concede that thoroughbass, a mere stenographic device, has no bearing on harmonic theory. If the use of figures has persisted in what generally passes for harmonic analysis, it attests to an atavistic respect for an old tradition rather than to an efficient and thoughtful method of its practitioners. The tradition, very useful at one time and well serving a particular purpose, loses its meaning by being transplanted to another stylistic challenge and different task. What do the figures 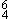 under a triad, for instance, tell a student that he could not directly read off the "longhand" of the notated score?
under a triad, for instance, tell a student that he could not directly read off the "longhand" of the notated score?
The touchstone of analysis is simple and unambiguous. Analysis must establish a relationship, otherwise it remains mere description. The relationship may be between anything and anything. The subtler the qualities uncovered, the more meaningful the analysis. If one points out, for instance, that a section in the beginning of a piece recurs later in another key, one has contributed to the analysis of the form; for the relationship is not directly audible or noticeable as the music first unfolds. Of a subtler nature might be the observation that an unfinished or interrupted melody is completed by a phrase heard much later; or that a counterpoint eventually serves also as double counterpoint at the twelfth. Mere description, on the other hand, would be statements that the opening of the Eroica Symphony, for example, is in E-flat major; or that the ending of Alban Berg's Lyric Suite is indefinite; or that the first comes of the subject in the C-major fugue from the The Well-Tempered Keyboard I has a counterpoint below it.
With this criterion for analysis in mind, one must readily concede that the roman and arabic numerals commonly in use today to indicate chords on the various scale degrees do not qualify as analytic tools. The former indicate positions, not relations. Analytic inquiry is not served by being told that a notated G-major chord in a C- major composition stands on the fifth degree of the scale. Besides thus being superfluous to a musical reader, roman numerals can also blur rather than clarify issues, as in the case of the sixth degree, which in major is the relative of the tonic but in minor of the subdominant. An occasional "V of something" hints at a relationship but at one of the passing instant without elucidating the reason for the "something" in the overall context. The arabic numbers accomplish even less, for all they do is transcribe notes visible to any literate musician into nonmusical symbols.
Harmonic relationships that underlie analysis are clarified by recognizing the functions of chords, that is, their behavior, their inherent tendencies, their potential energy. At the core of functional harmony stands the proposition that all chords, without exception, are in character either tonic, subdominant, or dominant. Whatever the appearance of any chord, it acts as a representative of one of these three functions.1
In tonal harmony, all currents run from the neutral and given tonic to the two dominants and back again. The greatest and basic harmonic tension exists between the point of rest in the middle and the polar pull in two directions from the fifth above and the fifth below. (One must not make the error of assuming that "sub"-dominant means "below" the dominant. The two dominants are equivalent, exerting their force on the central tonic from above and from below.) Many sound theoretic reasons have been given for the sovereign (one is tempted to say dominant) role of the upper and lower fifths. Here we need only refer to their springing from the monochord division and multiplication by 3 as the first interval right after the octave generation by 2; to the early appearance of the fifth in the harmonic series as the first nonidentical, nonconcordant, procreative interval; to the tetrachordal frame set by the two pitches around the tonic of the closed scale form; and to other such considerations amply documented in theory. Our primary concern with harmonic analysis may safely stipulate the theoretic basis without the obligation of pursuing it here on a big detour to our goal. Even musical jargon recognizes the special function of the fifth by calling it perfect in contrast to all other nonidentical intervals.
Our initial proposition implies a principle lying on a deeper level—polarity. In a sense, this general philosophic concept is beyond discussion; for everyone is free to accept or reject it. The evidence in its favor is very strong and has been successfully stated by many thinkers. Polarity explains a fact or event as resulting from the interplay of two opposite but complementary forces. Male and female create a child. Lightness and darkness together form a day. Thesis and antithesis produce a synthesis. The literature from Genesis and Plato to Goethe and Whitehead abounds in examples. In music we deal with high and low, up and down, major and minor, strings and winds (in Greek aesthetics), and frequency and wavelength (in modern physics). See Figure 1.
Figure 1. The numbers indicate frequency relations for the ascending series, wavelength relations for the descending series.

Functional harmony implies the polarity of the two dominants as the generative forces around the tonic. They stand for all tensions and dissonances around the consonant and restful unison of the tonic. On the premises developed thus far, we may now propose a procedure for harmonic analysis.
Triads on each degree of the major and minor scales yield the results shown in Figure 2.
Figure 2. Triads on each degree of the major and minor scales.
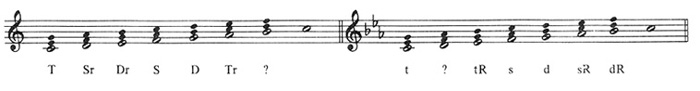
The minor scale is understood to be natural; the so-called harmonic and melodic versions are hybrids outside this stage of the discussion. The symbols are self-explanatory abbreviations for the three main functions and their respective relatives.2 Capital letters indicate major triads, lower-case letters indicate minor triads. The symbol sR, for example, defines the major relative of the minor subdominant. One notices that in the major mode the three principal functions have major triads (T, S, D). In the minor mode, they have minor triads (t, s, d). The respective relative triads are always in the opposite mode. These six main triads leave one chord in each mode undefined: there is no perfect fifth on the seventh degree in major, nor on the second degree in minor. These two chords evidently lie outside the basic formations. Musicians will understand that the identification of a triad by one of the six suggested names is much more than a description, be it by a roman numeral or terms like mediant or supertonic, all of which merely indicate a position. There is a significantly different quality to the concept of the two dominants. The move or tension D-T evokes a special, purely musical experience, quite distinct from an S-T experience. The relative triads, as their very name suggests, may act as substitutes. Thus the symbols D-Tr, for instance, tell us that the particular dominant current reaches a substitute for the tonic—a deception which the letters V-VI or a reference to the submediant do not convey.
The leading-tone current in D-T is so strong that the minor mode frequently borrows the major dominant for its own use. In the symmetrical case of s-t, the descending leading tone to the dominant is so strong that the major mode frequently borrows the minor subdominant for its own use. (I have regularly given the assignment to find minor subdominants, easily spotted by the minor sixth, in compositions in the major mode. The standard literature is full of them. Whereas one has generally taken the major dominant in minor for granted—witness the melodic and harmonic versions of the scale—the analogous case has been one-sidedly overlooked.) We may generally associate major with sharps and the dominant (the sensitive tone is raised), and minor with flats and the subdominant (the sensitive tone is lowered). The strongest possible basic cadence in either mode therefore sounds as in Figure 3.
Figure 3. The strongest basic cadence in either mode.

The current may run in either direction with equal force. See Figure 4.
Figure 4. The basic cadence with reversed current.

The basic three triads and their relatives are intensified by an added seventh. The seventh shows its origin as a passing tone from the octave to the sixth by the way it is properly introduced and resolved. The new tone does not change the original function. It clarifies, however, the two formerly unidentified diminished triads. The one on the seventh degree of the major scale emerges as a dominant seventh chord without root (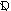 7). The one on the second degree of the minor scale reveals itself as a subdominant with a sixte ajoutée and without fifth (s6). Actually any proponent of complete symmetry of major and minor (which can be demonstrated without Riemann's unfortunate recourse to a hypothetical undertone series) will readily recognize the added sixth as a lower seventh moved up one octave. The charge in the two dominants shown in Figure 3 is thus further intensified by the additional leading tones, as in Figure 5.
7). The one on the second degree of the minor scale reveals itself as a subdominant with a sixte ajoutée and without fifth (s6). Actually any proponent of complete symmetry of major and minor (which can be demonstrated without Riemann's unfortunate recourse to a hypothetical undertone series) will readily recognize the added sixth as a lower seventh moved up one octave. The charge in the two dominants shown in Figure 3 is thus further intensified by the additional leading tones, as in Figure 5.
Figure 5. Intensified basic cadence.

When the two dominants unite against the common center, we find the chord given in Figure 6.
Figure 6. The two dominants combined.

Except for the two outer tones (the ascending and descending generators, according to some), the others are all sensitized leading tones. By themselves, they produce the diminished seventh chord, of which the special popularity and strength are precisely derived from the simultaneous action of both dominants. The leading tones of the dominant proper ascend, those of the subdominant symmetrically descend. The presence of the two outside points (C and G) would considerably weaken the function by anticipating most of the resolution. The preponderance of thirds in this diminished seventh chord, together with the stenographic thoroughbass mechanics, is probably partly responsible for the all too facile assumption of defining a triad as two superimposed thirds instead of a splitting of the fifth.
All other chords in tonal harmony are variants of the few elements described. The minor subdominant may be modified by replacing the rubbing fifth and sixth with the leading tone from above to the tonic. The resulting Neapolitan sixth chord is not, as one often reads, a first inversion of a major triad a halftone above the tonic (why?) but a sensitized subdominant 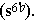 Analogously the one noncommital tone in any version of the dominant chord, the fifth, can be led to the tonic by a cogent downward leading tone. The resulting chords, shown in Figure 7, all retain their original dominant function.
Analogously the one noncommital tone in any version of the dominant chord, the fifth, can be led to the tonic by a cogent downward leading tone. The resulting chords, shown in Figure 7, all retain their original dominant function.
Figure 7. Variants of the dominant with leading tones to the tonic from above and below.

The telling characteristic is the augmented sixth between the two leading tones (best placed in the outer voices). The parallel fifths in the resolution of the German augmented-sixth chord are not a "tolerated exception sanctioned by Mozart" but the result of leading-tone currents. The perfect fifth produced by chromatic alteration (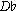 -
-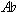 ) does not exist as a real harmonic position.
) does not exist as a real harmonic position.
Chords or chord progressions not occurring in the key are all secondary. Their own behavior, following the norms of any key, is less significant than the goal to which they lead and which they clarify. Their symbols are properly placed in parentheses, of which the contents are defined by the harmonic function immediately after it. The dominant of the dominant, (D)D, can also be notated as . See Figure 8.
Figure 8. Chopin, Prelude no. 20, mm. 1-4.

What functional analysis of this example shows is that the second measure parallels the first while temporarily emphasizing the subdominant region (sR). In addition to the renewed emphasis on the subdominant in measure 3, these opening three measures offer a forceful cadential preparation for arrival on the dominant (m. 4), which, moreover, establishes itself by its own secondary cadence.
Figure 9 shows a more complex, chromatic passage, with sharps and flats apparently pulling in all directions.
Figure 9. Wagner, Siegfried, act I, beginning of scene 2.

While this passage can be very well understood melodically as the unfolding of a bass progression from B through A to G, a harmonic analysis, which is our present concern, renders additional insights. The arrival point at C major identifies the tonic (which governs the entire scene between the Wanderer and Mime). The final cadential progression in our example, dominant to tonic, is, as the symbols immediately show, preceded by two identical phrases in sequence. Complicated as they may seem, each phrase pursues a standard cadential course in a secondary function of what follows.
Modulation, finally, is readily understood as a change of function, as shown in Figure 10.
Figure 10. Mozart, Piano Sonata, K. 282, first movement, mm. 1-9.

The tools offered by the preceding examples are adequate to the task of analyzing harmonically a large structure as much as a short phrase. The tonal arch spanning the twenty songs of Schubert's Die schöne Müllerin, which begins and ends in different keys, makes sense in the functional harmonic analysis shown in Figure 11, which reveals the underlying unity behind surface contrasts.
Figure 11. Harmonic structure of Schubert's Die schöne Müllerin.
No. Title Key Harmonic Function Specific General 1. Das Wandern B-flat tR T 2. Wohin? G T T 3. Halt! C S S 4. Danksagung an den Bach G T T 5. Am Feierabend a Sr S 6. Der Neugierige B (D)Tr D
7. Ungeduld A-flat (or SrP)
S 8. Morgengruss C S S 9. Des Müllers Blumen A (or SrP)
S 10. Tränenregen A-a (or SrP)-Sr
S 11. Mein! D D D
12. Pause B-flat tR T 13. Mit dem grünen Lautenbande B-flat tR T 14. Der Jäger c s S 15. Eifersucht und Stolz g-G t-T T
16. Die liebe Farbe b Dr D 17. Die böse Farbe B-b (D)Tr-Dr D 18. Trockne Blumen e-E Tr-TrP T 19. Die Müller und der Bach g-G t-T T 20. Des Baches Wiegenlied E TrP T
The results of this analysis can be read off the last column, in which the harmonic events have been reduced to their basic functions. The approach to the central climax "Mein!" has two stages, each reaching the dominant after preparatory subdominant cadential keys. The first of these dominants (No.6) appears in substitute form and thus does not compete with the only real dominant, D major, at the peak of the whole cycle. Singers are well advised to make a small caesura after No.6 and a real break after No. 11. In the descending curve of the plot, the subdominant disappears almost completely. The tonic, G major, more implied than established in the beginning, now asserts itself together with the increasing introspection of the hero. The last three songs offer different variants of the tonic, which reveals itself most clearly in the arch from No. 2 across No. 11 to No. 19. The first and last songs, five strophes each, form a frame around the actual story and justifiably use symmetrically corresponding tonic substitutes. In the two sections of the second half, the plot (external jealousy, internal suffering) is paralleled by the cadential currents (S-T, D-T).3
Because Bach chorales traditionally offer excellent material for harmonic analysis, Figure 12 supplies a worthy conclusion to our examples.
Figure 12. Bach, Chorale, "Jesu, der du meine Seele."

Even a casual first glance at the symbols shows that the harmonic rhythm, realized in the first half of the strophe (mm. 1-2) by the basic and strongest cadential functions (sD) is considerably accelerated in the second half (mm. 3-4); and that a similar acceleration occurs in the epode (mm. 9-16) before slowing down toward the end. The epode is further characterized by a noticeable prominence and intensification of relative substitutes. In any harmonic analysis of a Bach chorale, isolation of the arrival points is very telling: t D :|| dR tR D T. The departure from the tonic is straightforward. The return at first cadences on the relatives before setting everything right at the end.
Although in some respects obviously indebted to Hugo Riemann, this paper must not be interpreted as advocating one more system of analysis. Quite independently of any system and proceeding from generally fundamental facts of tonal harmony, I have tried to separate analysis from theory and theory from practice. The clarifying of distinctions is necessary and valid for any approach. A sharp formulation by Carl Dahlhaus may serve as confirmation and summary:4
Musical analysis . . . is either a means or an end. It aims at theory and is thus its first step; or it tries to do justice to a musical work as a particular individual formation. . . . Analyses deserving this title are, on the one hand, efforts to demonstrate the validity of a theory, of the system of functions and scale degrees; the possibility of a consistent and through its simplicity persuasive designation of chords by functional symbols or degree numbers then serves as proof; it reveals less about the work than about the theory. Or, on the other hand, an analysis should isolate the characteristics that distinguish the harmonic structure of one work from that of another. In this case it does not suffice to number the chords and to let the reader find in these numbers the special quality of the harmonic structure. The individual character of the chordal structures and relations must rather be expressly shown and articulated by an interpretation of the analysis: an analysis of a second order (of which the categories have hardly been developed). If—so one may conclude—an analysis functions neither as demonstration or proof of a theory nor as a conceptual transcription of the particularity of a work, then it is unnecessary: it appears as mere application of a nomenclature, as labeling, which says nothing because it is aimless.
1The following exposition of functional harmony follows in principle the original insights of Hugo Riemann while modifying them to a considerable extent.
2The terms relative and parallel have exactly opposite meanings in English and in German—a crossover of which readers should beware!
3For a more detailed structural analysis, see Siegmund Levarie and Ernst Levy, Musical Morphology: A Discourse and a Dictionary (Kent, Ohio: Kent State University Press, 1983), 311-14.
4Carl Dahlhaus, Analysis and Value Judgment, trans. Siegmund Levarie, Monographs in Musicology, no. 1 (New York: Pendragon, 1983), 9.


