This paper describes "integrated music learning" as a desirable way of combining different ways of learning musical relationships and shows how "menus, maps, and models" can be used to teach musicianship and theory through improvisation.1
Integrated music learning
Music learning is best when it is "integrated"—when it combines different ways of understanding musical relationships. Example 1 represents this idea with an eight-pointed star.
Example 1: Integrated music learning combines ways of kowing musical relationships.
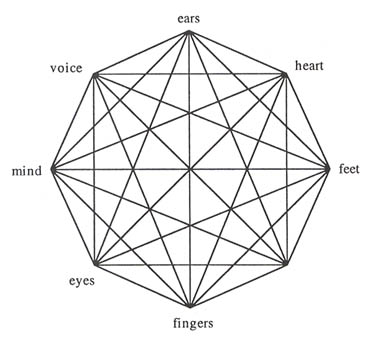
Each point represents one way of "knowing" musical relationships. One of the points is left blank to suggest that there may be other ways of knowing musical relationships. Consider the structure of the major scale. One may know intellectually (mind) that the major scale has half steps between its third and fourth and between its seventh and eighth scale degrees. One may be able to recognize visually (eyes) the locations of these scale degrees in music notation. One may recognize aurally (ears) the differences between third and fourth or seventh and eighth scale degrees. One may know vocally (voice) how to sing given scale degrees on command. One may know digitally (fingers) how to play a scale or a given scale degree on the piano. And upon hearing the fourth and seventh scale degrees resolve respectively to the third and eighth, one may feel the resolution emotionally (heart). We can also know things kinesthetically (feet); to know something kinesthetically is to feel it in or with any part of your body (I use the word "feet" because it reminds me of dancing, but conductors may prefer to think of this as "arms"). By the way, though it seems less obvious, I think we also may know kinesthetically (feet) about the structure of the major scale as we learn to associate its distinctive resolutions with the qualities of felt gestures.
Integrated music learning combines these ways of knowing. For example, someone may know intellectually that the fourth and seventh scale degrees are active tones that (in the right context) tend to resolve, respectively, to the third and eighth scale degrees. And the same person may have heard the resolution enough times to recognize it aurally as a familiar tonal event. But until that person associates that knowing-with-the-mind with that knowing-with-the-ears, he or she hasn't integrated the learning of that resolution in a way that would allow him or her to identify that resolution. Learning is thus a kind of association.
In my classes, I offer Example 1 as a checklist for students. I ask them to memorize it. And then we make sure that we not only learn all those aspects of each topic we study, but also find ways to integrate those aspects.
The diagram in Example 2 suggests how this might work. It is a flow chart that shows (left-to-right) that different ways of knowing some musical relationship can be combined by patterns of cognition that integrate that knowledge.
Example 2: In integrated music learning, the combinations of different ways of knowing some musical relationship are influenced by the structures of that relationship and the structures of the mind.
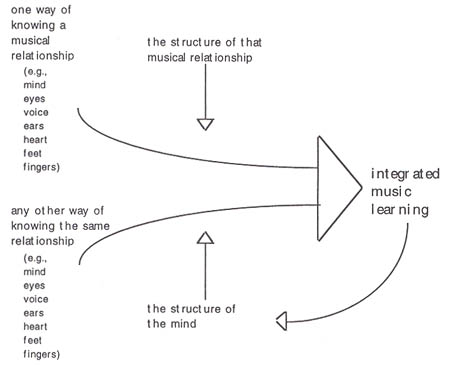
The patterns of that musical relationship influence how the different ways of knowing it can be combined. The organization of cognition also influences how the different ways of knowing can be combined. Finally, that combination (of different ways of knowing) influences further patterns of cognition.
You may have noticed—in learning or teaching almost anything—a frustrating paradox: "In order to know this you first have to know that . . . but in order to know that, you first have to know this." This paradox seems related to another one: "to learn something, you must already know it." (The idea that "learning is simply discovering things we already knew" may seem to reflect eastern mysticism or even "occult" thinking, but the same idea also has roots in the western tradition. Plato returns repeatedly to this idea in his Dialogues—for example, see especially the "Meno"2). One interesting thing about this model of integrated music learning is that it suggests how and why it is true that "to learn something, you must already know it." Putting together different ways of knowing musical relationships seems to require that we already know that relationship in different ways. Fortunately, this also comes around full circle: anytime we combine two ways of knowing a musical relationship, each of those two ways of knowing is strengthened.
The importance of patterns—musical and cognitive
Because I want to enlist students as partners in the search for patterns of thought and patterns of music, I often include the following game in the first class meeting of a course on music theory or musicianship.3
In this game, I ask students to memorize the following string of numbers after looking at them for only three seconds.
78 9101 1121 314
Then I ask them to write the numbers down. Occasionally, some get the whole string. But usually, there are vacant spots (most students get the beginning or ending right; and often some of them get the right number of "chunks," many beginning and/or ending with the right number, but containing problems in the "middles"). Then I ask them to think about how and why the problem is difficult. This often leads to fruitful discussion about beginnings, middles, and ends; about boundaries and "chunks"; about patterns, grouping, and understanding; and about sense and non-sense.
Because some students are made uneasy by numbers, I also ask them to do the same task with letters.
Thissen ten ceise asytome mor ize.
The purpose of this experiment is to show two things: first, that the ease with which we memorize something is related to how well we understand it; second, that the ease with which we understand something is related to how we group its parts. When those same numbers are grouped as "7 8 9 10 11 12 13 14," or the same letters are grouped as "This sentence is easy to memorize," students find them easier to remember. Asking them to study these second groupings—and counting out the full three seconds in which they studied the first groupings—helps drive home the point that we don't need to "memorize" what we "understand."
The ideas that make up the content of music-theory courses would be difficult to learn if they seemed as random as the first collections of characters. But to some students, music theory consists of just such random collections of rules. Such students need to learn that if they will find the patterns behind the rules—that is, if they understand the principles behind the rules—then those ideas will be much easier to learn. (And teachers who take the challenge implied hereof helping students to find the patterns behind the rules—may find that their teaching becomes more successful and more enjoyable.)
Notice that this means that learning should be easy. Of course, it sometimes takes a long time to make it easy, but finding the best way to do something often means making it easier to learn. It may be good to spend a lot of time learning. But—especially in music—working too hard at learning things may be counterproductive. Theory that is learned with great effort (like the memorization of nonsense) is likely soon forgotten. Likewise, musicians who learn to play a piece with difficulty—instead of practicing a sense of ease into its performance—may convey a sense of their own effort and/or discomfort to the detriment of the expressive meaning of that piece. Robert Trotter liked to draw my attention to the use of the word "try"; and I have noticed (especially when teaching sightsinging, for example) that the images (or kinesthetic senses) that students attach to "trying" often get in the way of their learning.
Furthermore, learning should be fun. Students who look forward to the rewards of perseverance can often stay with an otherwise unpleasant task a long time. But teachers who help students find ways of making learning an engaging activity may be teaching those students an important lesson about how to learn music. If one can attach a sense of play to learning, then it is more likely to be easier and thus more successful.
The importance of improvisation
One arena of music-making that usually involves a sense of play is improvisation. In fact, it is easy to assemble a long list of reasons to include improvisation in our teaching and learning. The composers whose music forms the central part of modern instruction in music schools learned "music theory" through improvisation; learning harmony by studying thoroughbass not only teaches harmony and voice leading through improvisation, but it presents harmony as a subject of immediate musical as well as intellectual interest. The quality of freedom within constraints that we associate with good composers is aptly referred to as "improvisational" (in fact, for Heinrich Schenker, whose ideas, acknowledged as such or otherwise, form an important part of modern training in music theory, this "improvisational" quality, as he called it, was the sine qua non of music of lasting value4). For many of our students, improvisation is an important means of expression. Those who play jazz and popular music will want to learn to improvise. But so will organists who play church services, music educators who want to improve or adapt the materials readily available to them, choir directors and others who wish to accompany groups in varied ways, and music-theory teachers who want to be able to offer compelling and focused musical examples when answering student questions. To these traditional, artistic, and practical justifications, we can add a pedagogical one. This pedagogical justification flows from the reasons that we require music-theory courses of all music students and only of music students. The best reason is that we believe it teaches skills that will support their music-making, music-teaching, and music-learning pursuits. And such theoretical ideas (or rather, such musicianship skills) are really only useful in those activities if they can be accessed in real time (to use the computer jargon that is increasingly and understandably popular now). Knowing facts about music (or about a foreign language or about how to ride a bicycle) is only useful if those facts can be brought to bear as quickly as the musical situation (or the opportunity to speak or the chance to steer a bike) requires. Improvisation not only requires that those skills be accessible, but also makes them available.
Finally, if any more justification were required, we might turn to the requirements of the National Association of Schools of Music (NASM). Here is a quotation from their most recent Handbook:5
1. Beyond traditional exercises in beginning theory, students must develop composition and improvisation skills. Approaches might include: imitation of various musical styles, experience in original composition, experimenting with various sound sources, and manipulating the common elements in non-traditional ways.
2. Continuous development of improvisational skills is strongly recommended, whether as an aspect of composition, musicianship, or performance studies.
Despite all this I believe that, although many music-theory courses involve a fair amount of composition, few involve much improvisation. One could argue that any assignment that asks students to compose within given constraints could easily be turned into an assignment that simply asks students to improvise within those same constraints. But if care is given to the nature and ordering of those constraints, the results may be more musically and pedagogically satisfying. The purpose of this paper is to show how we can use improvisation on specific harmonic patterns (called "model progressions") to foster integrated music learning.
Harmonic function and expressive meaning
The discussion that follows presents its model progressions in the light of a specific theory of harmonic function in tonal music. Thus, the following discussion might be seen both as (1) advocating that theory of harmony, and as (2) advocating the idea of teaching musicianship through improvisation on model progressions. However, these two ideas should be seen as separate. The central thrust of this article is that of teaching musicianship through improvisation on model progressions—a way of teaching that could also be used for instruction based on a different theory of harmony.6
The specific theory that guides my selection and use of model progressions here is an evolving one that I have described elsewhere.7 According to that theory, we tend to hear tonal motion as purposeful action within a dynamic field of musical forces. Harmony is thus best described as an emergent property of the interaction of the musical forces generated by the individual melodic patterns that make up a musical texture.
Harmonic motion is, in this view, a powerful and vivid aspect of expressive meaning in music. We experience musical motion as a mapping of physical gestures onto musical space. And we experience specific harmonies in many different ways: they may be heard as pushing or being pulled, flowing toward or evaporating from, interrupting or interrupted, suspending action or provoking it, etc. The expressive meanings of individual harmonic motions contribute to, and derive their meanings from, archetypal patterns of harmonic motion—ordered patterns in which individual chords are heard as representatives of functional categories whose functions are determined by their roles in phrases that coalesce around cadences. Thus, I present the model progressions together with a "menu" and a "map" that show their place within a pedagogical sequence based on the harmonic functions of various chords within phrases.
For practical musical purposes—for performers, composers, and teachers—it is the shaping of those individual melodic patterns that provides the most productive focus of creative activity. Thus, the model progressions are also presented in a way that highlights the melodic patterns upon which they are constructed. That means that this theory departs from some traditional accounts in that it emphasizes chord basses and voice-leading patterns more than chord roots and root motion.
A sample unit
To make the discussion that follows more concrete, see Example 3.
Example 3: A sample menu, map, and model progression.
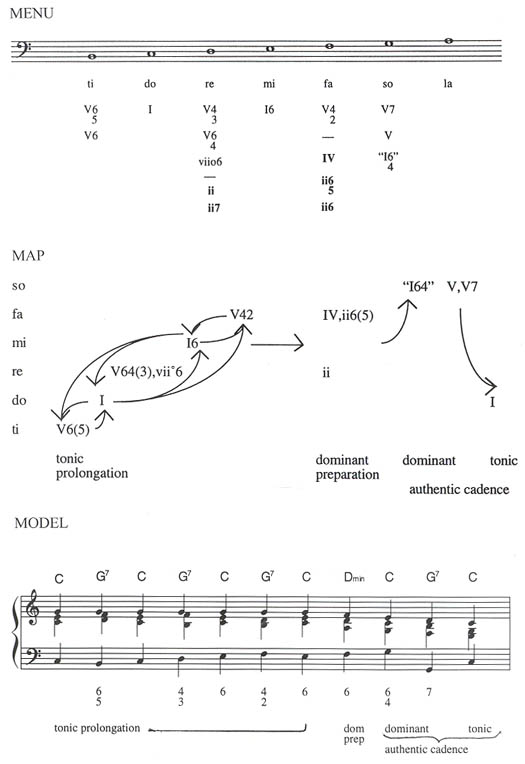
This unit shows a menu, map, and model progression in major that might be encountered late in a freshman-year course on diatonic harmony.8
Menus—the vocabulary of chords
The menu lists, for each degree of the major scale, all of the chords that can appear in progressions that follow the map of this unit, or all of the chords that students will have encountered by the time the unit is completed. Chords that are new in this unit are in boldface. Because each new menu adds a small number of new chords, students will gain increasing confidence as their "vocabulary" grows. By the way, students also like using these menus for their harmonic dictation exercises, so that harmonic dictation becomes a "multiple-choice activity" focused on bass lines. This is as it should be—experienced listeners do not ask "What were the chords in that progression?," but "Which pattern of chords was that?" or "How did that progression differ from one I know?," and even more important, "What is the expressive meaning of the bass line?"
Thus, each chord is listed according to its bass note—not its root. This reflects the fact that the two chords called IV and ii6 or the two chords called V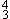 and vii°6 often have more in common (in terms of their function or expressive meaning) than the two chords called I and I
and vii°6 often have more in common (in terms of their function or expressive meaning) than the two chords called I and I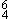 or the two chords called V and V
or the two chords called V and V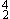 . On the other hand, it is also true that two chords with the same bass note may have different functional or expressive meanings. For example, ii6 and V
. On the other hand, it is also true that two chords with the same bass note may have different functional or expressive meanings. For example, ii6 and V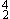 have the same bass, but usually have very different functions. This is the reason for the horizontal line separating chords listed under the second and fourth scale degrees; some of these chords appear within tonic prolongations and others function as dominant-preparation chords. Of course, even a single chord may have different functional or expressive meanings in different contexts, but if the question is "Which helps me more, thinking of the bass line or knowing the chord roots?," then an answer based on aural perception and practical needs should emphasize basses over roots. In fact, to be most consistent with this emphasis on basses over roots, the menus may also be given as bass notes whose possible chords are listed only by figured-bass symbols (that is, with no Roman numerals).9
have the same bass, but usually have very different functions. This is the reason for the horizontal line separating chords listed under the second and fourth scale degrees; some of these chords appear within tonic prolongations and others function as dominant-preparation chords. Of course, even a single chord may have different functional or expressive meanings in different contexts, but if the question is "Which helps me more, thinking of the bass line or knowing the chord roots?," then an answer based on aural perception and practical needs should emphasize basses over roots. In fact, to be most consistent with this emphasis on basses over roots, the menus may also be given as bass notes whose possible chords are listed only by figured-bass symbols (that is, with no Roman numerals).9
Notice that the menu also gives solfege syllables. Regardless of what solfege system(s) one uses for sightsinging, there are advantages in using the same one(s) here. The biggest advantage is that doing so advances integrated music learning by encouraging students and teachers to relate their aural and intellectual understanding of these chords.
This unit includes enough of the most basic diatonic chords in major to illustrate how the maps, described below, organize progressions involving these chords.
Maps—the functions of chords
The map, like a bus-route map, shows all the "legal" paths that experienced listeners expect progressions to take. Such "legal" routes follow the one-way arrows in only the direction they point, always taking a course that begins with a tonic prolongation at the left and that ends with an authentic cadence at the right. The map is also laid out so that it shows "elevation"; each chord occupies a vertical position on the page that is determined by the pitch of its bass note. The obvious analogy—that a phrase is like a journey—is one that helps students think about phrases in ways that may improve many aspects of their musicianship.
Of course, music does not always do what we expect it to, but the maps offer a context for making useful generalizations about common-practice phrases. For example, the theory described here argues that all phrases do one of three things: (1) they take a "legal route" on one of the maps; (2) they connect two points on a map through a contrapuntal procedure (such as a sequence); or (3) they purposefully depart from the map to create a special effect.
In fact, using these maps over the course of a term—building them up—allows one to make an important larger point about expectation, phrase structure, and the perception and explanation of both. One earlier map includes I and I6 in the tonic prolongation, but does not include inversions of V7 and vii°. In terms of that earlier map, I-I6 is a legal route, but I-vii°6-I6 (a legal route on the map in Example 3) is a case of (2) above, a contrapuntal connection between two points on that earlier map. The map in Example 3 has thus absorbed an "exception" into what is now considered basic. A later map shows how vi and IV6 function in a deceptive cadence, and this emphasis on defeating an expected cadence leads to mentioning the "evaded cadence" in which a cadential dominant leads, via V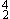 , "back" to I6. In terms of the map in Example 3, those defeated cadences are instances of (3) above, purposeful departures from the map. The later map has thus again absorbed an "exception" into what is considered basic. As we build up our knowledge of chords, musical procedures, and "how things work" (in life as in music), we understand the complex in terms of the simple and we understand the unexpected in terms of the expected. And our new, more-complex models then form the basis for understanding ideas that are even more complex.
, "back" to I6. In terms of the map in Example 3, those defeated cadences are instances of (3) above, purposeful departures from the map. The later map has thus again absorbed an "exception" into what is considered basic. As we build up our knowledge of chords, musical procedures, and "how things work" (in life as in music), we understand the complex in terms of the simple and we understand the unexpected in terms of the expected. And our new, more-complex models then form the basis for understanding ideas that are even more complex.
Model progressions—frameworks for learning musicianship skills including improvisation
Each unit includes one model progression (more could be included, but in my experience, it is better to let one well-learned example stand for the idea studied and let students relate similar progressions to that model).
Notice that certain features of the model progression support its practical purposes. In many of the model progressions, all voices end on the note that begins some lower voice (this makes it easy to sing the progression with a group of singers as a round). The chords are labeled with lead-sheet symbols above the soprano and figured-bass symbols below the bass (Roman numerals and figured-bass symbols need not be mixed). Below the figured-bass symbols, an analysis indicates the function of each chord, showing how the progression follows the map.
This model progression is set in four voices, but others are set in three. For instance, Example 4 shows a progression, set in three voices, that is important in styles ranging from that of baroque composer J. P. Rameau to that of jazz-pianist Bill Evans.
Example 4: The complete circle-of-fifths diatonic-sevenths model progression.

Applications—sample exercises using the menus, maps, and models
Before reading through the list of suggested exercises (Example 6) using the menus, maps, and models, note that where any of them say "sing" they could say "sing with syllables that describe what one is singing." By "syllables," I mean any "lyrics" that describe musical relationships created: moveable syllables (such as "scale-degree numbers" or "moveable-do solfege"), note names (these can be the "traditional French fixed-do solfege" or "monosyllabic chromatic English letter names"10), intervals above the bass, chord membership, etc. Example 5 shows some of these.
Example 5: Different types of "solfege" describe different musical relationships.

Note also that many of the exercises are for a group of musicians, and say "One improvises . . . and the others . . ." In such cases, "one" can be a student or the teacher, and the music to be improvised may be improvised on the spot, or rehearsed, or even notated and then performed. (Students should be encouraged to see how thin the line between improvisation and composition really is.)
Finally, while one could omit those exercises involving keyboard performance and still get a great deal out of what follows, I believe that that would be both unnecessary and undesirable. These exercises do not demand physical dexterity at the keyboard—they may be musically challenging, but they can be technically easy (most involve singing while playing with one hand, playing one voice in each hand, or playing simple homophonic textures at no specified tempo). But more important, if the point is integrated music learning, then perhaps we should adjust our curricula to students' keyboard skills—this seems better than "covering" material in a way that encourages students to forget rather than apply their knowledge.
Example 6: A dozen exercises using maps, menus, and models
(1) One points to a location on the map. Others sing the bass and/or play a chord on the piano. From that location, the one that is pointing moves to another location via a "legal route" on the map. The others follow. The process continues until a final tonic is reached.
(2) One improvises a phrase that follows the map. Others, by hearing the function of each harmony, trace that route on the map.
(3) One improvises a phrase that follows the map. Others label some or all of the chords by choosing from the menu.
(4) One improvises a phrase (in two or more voices) that follows the map. Others notate the soprano and/or bass.
(5) One notates a phrase (with Roman numerals, lead-sheet symbols, a figured bass, or standard music notation) that does not follow the map and others say how or why it departs from the map.
(6) While playing the bass line of the model progression, sing (or play on the piano) one of the upper voices.
(7) With a group, sing a round composed of successive lines of the model progression, each new singer beginning when the most recent singer reaches the tonic again (imagine a repeat sign just before the final tonic chord that says "go back to the beginning and sing the part that begins on the pitch you would have ended on").
(8) While playing the bass line of the model progression, sing (or play on the piano) one of the upper voices, with improvised embellishments.
(9) While playing the bass line of the model progression, sing (or play on the piano) two of the upper voices by alternating between them and/or filling the space between them with passing tones.
(10) Arpeggiate the model progression vocally, starting and ending each arpeggio with the bass. (The result is a series of close-position chords that will not necessarily imply good voice leading, but it will help students to "chunk" the voices into chords.)
(11) To the accompaniment of some realization of the model progression (including but not necessarily limited to just the bass line), one improvises a melody that fits that progression. Others, on an answer blank that reproduces the model progression (like Example 7), notate that melody.
(12) Transpose the model progression, or any of the above exercises, to another key.
Example 7

All these suggestions flow rather naturally from the menus, maps, and models. But one can also develop additional exercises for specific problems by considering the ideas that lie behind the menus, maps, and models. For example, consider the following sequence of activities for improving students' speed and accuracy in identifying the different positions of V7.
(a) Listen to an isolated chord (some position of V7);
(b) Sing the bass of that chord;
(c) Sing the two-note pattern that resolves that bass note (so-do, ti-do, re-do, or fa-mi);
(d) Assign solfege syllables to that two-note pattern; and then
(e) Determine the position from the bass syllable (so=V7, ti=V, re=V
, fa=V
).
Eventually, some students will integrate these steps into instantaneous recognition. Notice that at this stage it would appear that students are not identifying a chord, but a function (we hope!). That is, they are hearing a chord and recognizing it as an instance of a category of chords that all have the same function (that is, a passing or neighbor chord within a tonic prolongation) and the same bass note. Here is a list of those four categories, including additional chords with the same function and bass note: (so=V7, V; ti=V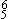 , V6, vii°; re=V
, V6, vii°; re=V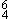 , V
, V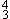 , vii°6; fa=V
, vii°6; fa=V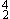 , vii°
, vii°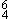 ). Notice that the first chord in each category is a different position of V7 and that the other members of the category may be regarded as incomplete versions of that position of V7. It is consistent with the ideas advanced here to suggest that time spent refining that identification is time taken away from the development of more important skills—after all, the musical justification for doing this kind of identification (whether in the context of traditional dictation or as in some of the alternative exercises suggested above) is the fact that harmonic function informs expressive meaning, and that it is expressive meaning, not correct chord labels, that we are concerned about. When my tests do include dictation problems asking for specific labels (which they do less and less frequently now), I award partial credit for chords of the correct category—and I make sure that students understand why I do so.
). Notice that the first chord in each category is a different position of V7 and that the other members of the category may be regarded as incomplete versions of that position of V7. It is consistent with the ideas advanced here to suggest that time spent refining that identification is time taken away from the development of more important skills—after all, the musical justification for doing this kind of identification (whether in the context of traditional dictation or as in some of the alternative exercises suggested above) is the fact that harmonic function informs expressive meaning, and that it is expressive meaning, not correct chord labels, that we are concerned about. When my tests do include dictation problems asking for specific labels (which they do less and less frequently now), I award partial credit for chords of the correct category—and I make sure that students understand why I do so.
Summary
Integrated music learning combines aural, vocal, visual, intellectual, digital, kinesthetic, and emotional understanding of musical relationships. If the focus of that learning is to understand the expressive meanings of those musical relationships and the intent is for that learning to benefit the practical and creative activities of performers, composers, teachers, and scholars, then much is to be gained from using improvisation in that learning. Menus, maps, and models allow students and teachers to approach the use of improvisation as a tool for developing musicianship skills with confidence that their experience can easily be made theoretically consistent, pedagogically sound, and musically rewarding.
1Please address communications to Steve Larson/University of Washington/MUSIC/Box 353450/Seattle, WA 98195-3450/ This email address is being protected from spambots. You need JavaScript enabled to view it./(206) 543-9212.
2Plato, "Meno," translated by W. K. C. Guthrie, in The Collected Dialogues of Plato, edited by Edith Hamilton and Huntington Cairns (Princeton: Princeton University Press, 1961), 353-384.
3I have described this game in another article, "Another Look at Schenker's Counterpoint" (Indiana Theory Review 15/1 [1994]: 35-52). That article also makes some specific suggestions for the study of counterpoint that follow from the ideas behind this game.
4John Rink, "Schenker and Improvisation," Journal of Music Theory 37/1 (1993): 1-54.
5National Association of Schools of Music, 1995-1996 Handbook (Reston, VA: NASM, 1995), 72.
6A review of other theories or of published textbooks is beyond the scope of this article. However, I would like to mention two textbooks. The textbook by Gary E. Wittlich and Deborah S. Martin, Tonal Harmony for the Keyboard: With an Introduction to Improvisation (New York: Schirmer Books; London: Collier Macmillan; 1989), is based on basic tonality-defining patterns and patterns that elaborate them, and it uses those patterns in improvisational activities. Although it does not deal with improvisation, Arthur J. Komar, Linear-Derived Harmony (Cincinnati: Ovenbird Press, 1992), gives an account of three- and four-chord harmonic patterns derived from combinations of three- and four-note melodic patterns consistent with the ideas discussed here.
7This theory has been shaped by my work with Douglas Hofstadter on artificial intelligence and musical creativity. My article "On Rudolf Arnheim's Contributions to Music Theory" (Journal of Aesthetic Education 27/4 [1993]: 97-104), describes some of the ways in which the theory is inspired by Rudolf Arnheim's applications of gestalt psychology to the perception of art. Another essay, "Scale-Degree Function: A Theory of Expressive Meaning and Its Application to Aural-Skills Pedagogy" (Journal of Music Theory Pedagogy 7 [1993]: 69-84), describes the theory in greater detail, cites experiments in psychology and music cognition that support the theory, and offers a series of suggestions for developing aural skills based on the theory. "Another Look at Schenker's Counterpoint" re-examines theoretical and pedagogical issues in Schenker's Counterpoint in light of this theory of expressive meaning. "Modeling Melodic Expectation: Using Three 'Musical Forces' to Predict Melodic Continuations" (Proceedings of the Fifteenth Annual Conference of the Cognitive Science Society [1993]: 629-634) describes a computer model based on the theory and compares the behavior of that model to the behavior of subjects in a psychological study. A presentation/panel, entitled Applying a Theory of Expressive Meaning in the Written- and Aural-Theory Classrooms, at the 1994 meeting of the College Music Society, featured two papers that discussed further pedagogical applications of the theory: one by Robert Hurwitz and myself entitled "Step Collections in Aural Theory" and one by William Pelto entitled "An Alternative to Rule Memorization for Written Theory." And a detailed analysis of the implications of this theory for clarifying the concept of prolongation, as used in Schenkerian theory, was offered in "Questions About Prolongation: Terminology, Perception, and Expressive Meaning," delivered to the 1994 meeting of the West Coast Conference on Music Theory and Analysis in Oakland and to the University of California at Santa Barbara's 1994-95 "Distinguished Lecture Series."
8The unit immediately following this would be an analogous one in minor. The analogy is not always exact, however; for example, the root-position supertonic chord in minor (ii°) is a diminished triad, which, because of its sonority, does not often play the same role in minor as the minor supertonic chord does in major. But note that the analogy is the most natural and compelling in terms of harmonic function and expressive meaning when it is made between parallel modes—not between relative modes. This fact is a strong argument for the use of analytic symbols and solfege systems that preserve this analogy by using the same symbol for chords or notes of the same function (i.e., "V" for the dominant chord, "do" or "one" for the tonic scale degree, regardless of mode). This does not argue against the use of key-dependent symbols (such as lead-sheet symbols for chords or traditional fixed-do solfege) for certain applications, but it does argue against a Roman-numeral system for harmonies that uses "I" for the tonic in major and "vi" for the tonic in minor (I have heard such systems advocated). And it does argue against a movable-do system that uses "do" or "one" for the tonic in major and "la" or "six" for the tonic in minor. While some pedagogues immediately see the disadvantages of calling the tonic triad "vi" in common-practice pieces in minor, the same musicians may inconsistently advocate "la-based minor" for the same repertoire.
9Although its terminology differs, the approach of Robert Hurwitz—who discusses "notational roots," "acoustical roots," and "functional roots"—is not only consistent with the ideas advanced here, but an inspiration for some of them.
10"Monosyllabic chromatic English letter names" is my name for a solfege system that has been proposed, with slight variations, by a number of authors. For example, see the system called "adapted English note names" in Ray Robinson and Allen Winold, The Choral Experience; Literature, Materials, and Methods (New York: Hagerstown, San Francisco, and London: Harper's College Press, 1976), page 241.


