Abstract
All tuning systems except equal temperament (ET) have small irreconcilable mathematical discrepancies. In particular, just intonation (JI), espoused by Zarlino and other Renaissance theorists as an ideal tuning system, was already known in the 17th century to have problems wherein singers using it would tend to go globally flat. Yet, some recent psychological studies have indicated that singers do somewhat favor musical segments tuned in JI, over ET or Pythagorean tuning. I present a methodology whereby choral directors preparing a piece can understand where and how intonation problem spots might occur in non-ET settings; how many, if not all, of them can be ameliorated; and whether some passages perforce must be mistuned. It draws on the history of tuning and cognitive psychology to present a system termed “extended JI,” which expands standard JI by having multiple shadings of intervals that differ slightly in frequency but “sound the same.” I argue that singers already use this principle unconsciously when harangued to “Think high!” while singing descending intervals. By expanding the process of dynamically correcting tuning discrepancies, choirs can present striking non-ET performances of chromatic music without going globally flat. A detailed analysis of Lasso’s Prophetiae Prologue is given as a case study; examples from Bruckner and Wagner are also discussed.
This title of this essay may seem absurd. The devil in the details, of course, is exactly what is meant by that seemingly innocuous phrase, “in tune?” Some readers no doubt immediately thought, “Just have a piano accompany the choir!” This just moves the question a step to the left. Being “in tune” for the choir would be defined as “singing the same pitches as a piano,” but what then does “being in tune” mean for the piano? That might be a satisfactory answer if “being in tune” is taken to mean, “This piano plays precisely the frequencies of equal temperament with A440 (or whatever the reference frequency may be).” The intuitive concept of “being in tune” for Western listeners—and many performers—has, however, a mostly unstated connotation of using intuitively “pure” acoustic intervals. Equal temperament (henceforth, ET) uses anything but: only the octave is pure, at 2:1. All non-octave intervals in ET have as frequency ratios irrational numbers: some power of the twelfth root of two, given the usual twelve pitches per octave. This is most definitely not “in tune” with any acoustically pure interval. Furthermore, the physics of piano construction requires that even octaves be tuned wider than the acoustical 2:1 ratios, so they also do not adhere to strict ET. Thus, “have the choir match pitch to a piano” arguably means that nothing will be “in tune.” We start to see the subtleties involved: as Lewis Fry Richardson laconically noted in an essay that was a precursor to the study of fractals, in reply to his rhetorical question “Does the Wind Possess a Velocity?” as a section heading, “This problem, at first sight foolish, improves on acquaintance.”1
The question in the title is, in fact, quite interesting if we try to perform not only the Prophetiae Prologue, but indeed almost all pieces of music using various proposed non-ET systems. Chromatic music contains thorny sections; but problems can occur even in very simple music. It is, in fact, trivial to construct a five-note diatonic melody that must necessarily go flat if performed according to the system of just intonation (henceforth, JI). One begins to wonder whether it is theoretically possible to “stay in tune”—I have still not yet defined the concept rigorously—with respect to any system or some pieces, or if they perforce will have “out of tune” passages (scare quotes are hence dropped), whatever that means.
Choral directors clearly have a strong interest that their choirs sing in tune. Some of their training involves learning to recognize spots where choirs can mistune. This process is, however, intuitive and informal. Usually, only experienced directors can articulate what they are going after. The issue is also present for other instruments such as strings that permit intonational pitch adjustments, but I will restrict my remarks to choirs. I present a methodology that choral directors and other performers can use in preparations to analyze where and how problem spots might occur. It uses concepts from cognitive psychology and the history of tuning; and as such, needs (horrors) a tiny bit of math—but nothing beyond fifth-grade fractions. The “devil in the details” caution in the second sentence of this essay warns that some formal rigor is warranted. While I will keep such formalism to a minimum, some likely surprising problems will appear.
In this paper, I first provide a short historical context for Lasso’s early motet cycle Prophetiae Sibylllarum, and summarize prior analyses of the cycle’s Prologue. In the second part of the paper, I offer a minimal technical tutorial on tuning systems. I emphasize minimal, because discussing tuning can quickly turn into a debate that is beyond the scope of this paper.2 However, a minimal technical introduction is necessary to help understand how and where non-ET systems have tuning difficulties. I also offer some pertinent information in cognitive psychology regarding categorical perception. To end this section I present a system called “extended just intonation” and argue that singers already use it unconsciously. The third section of the paper is a detailed analysis of the Prophetiae Prologue, investigating to what extent it can be sung in this tuning system. In the fourth section, I apply this methodology to two chromatic common-practice era pieces. I conclude with a general assessment of the merits of the proposed approach.
I. Lasso, the Prophetiae Cycle, and Analytic Literature on the Prologue
As Renaissance music scholars attempted to absorb the rediscovered Greek treatises, they were particularly struck by reports that different rhythms and genera of tuning generated profoundly diverse affective responses in listeners. Various Renaissance avant-garde composers tried to replicate these reported powers, resulting in a body of extremely chromatic music. Gesualdo is the most famous case, but more mainstream composers like Marenzio and Monteverdi also wrote such music.
Some highly chromatic pieces (for example, Giovanni Macque’s Consonanze stravaganti3) seem to be exercises for the sake of pushing the envelope, but others were intended for serious performance. Monteverdi’s Lamento d’Adrianna is one. Another is Lasso’s Prophetiae Sibyllarum for four voices a cappella, consisting of a Prologue and twelve prophecies. The text of the Prologue (Example 1, in a new transcription from the part books) reads in translation: “Polyphonic songs which you hear with a chromatic tenor, these are they, in which our twice-six sibyls once sang with fearless mouth the secrets of salvation.”4
Figure 1. Prologue score.

While Lasso (1532-1594) is not usually associated with extreme chromaticism, he did not avoid it if he felt its use was musically justified. Some of his chromatic works had an impact on contemporary practice in England at the very least.5 The Prophetiae cycle has been dated ca. 1558, as a gift to his patron Albrecht V of Bavaria; intended for private performance, it was published by Lasso’s son Rudolf ca. 1600.6 Since the 1960s the Prologue has been the subject of a flurry of analyses. Such interest seems to stem from its concise presentation of intriguing issues: it is an exemplar of relentless chromatic shifting, with major and minor triads built on twelve pitch-classes in twenty-five measures. Why the other motets have not generated similar interest is a mystery; perhaps they’re considered merely “more of the same.”
Such extremes led Edward Lowinsky to term the piece a “magnificent example” of “triadic atonality.” Most of his analysis has been attempts to show that the extreme chromatic shifts allow the piece to be considered functionally atonal, if such term is not an oxymoron.7 There is, though, method to Lasso’s madness. As Karol Berger has noted,8 Lasso does not make use of all available enharmonic spellings, and in fact avoids certain enharmonics (e.g., A♯) as much as possible. At the opposite extreme, William Mitchell dubiously tried to demonstrate the existence of a Schenkerian Ursatz in the piece, thus raising it unequivocally to the rank of “masterwork.”9 Other analyses are by Berger, William Lake, and Henry Klumpenhouwer.10 Of these, Klumpenhouwer’s is the most interesting from the standpoints of intonational and performance analysis; I will return to it at the end of the next section.
II. Tuning + Cognitive Psychology
IIa: Tuning Systems and Their Inherent Problems
There have been four major tuning system categories in European music: Pythagorean tuning (henceforth, PT), JI, mean-tone temperament, and ET. PT was the first, and for many centuries, the only system. It uses acoustically pure 8°s, 5°s, and 4°s11 at 2:1, 3:2, and 4:3 respectively. Only ratios of the first four integers—the tetractys—were consonances. Other intervals were derived from these; so, the limma—for us, the diatonic semitone between, for example, E-F—is L = 4° - (M2+M2) = 4:3 / (9:8 x 9:8) = 256:243 = 2**8 / 3**5. PT is a “3-limit system:” its ratios use only powers of two and three.
JI was proposed in the Renaissance by Ramis, and promoted by Zarlino among others. It additionally uses acoustically pure major/minor thirds of 5:4 and 6:5; Zarlino’s semi-mystical senario incorporated the consonances of Renaissance theory in the consecutive ratios of the series 1:2:3:4:5:6 as an expansion of the tetractys. It is thus a 5-limit system. Table 1 shows the JI ratios for pitches relative to C.
Table 1. Simple 5-limit Just Intonation for Referent = C.
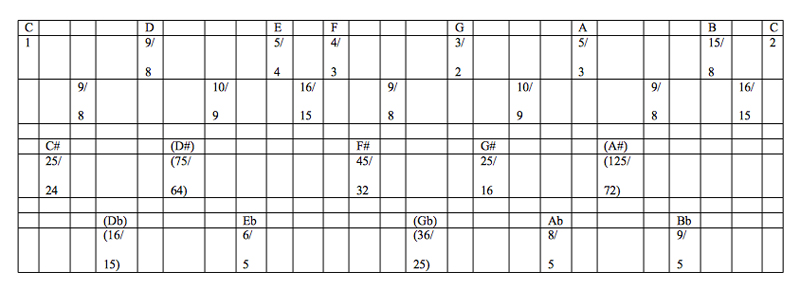
Note: The lines immediately below pitch names give their frequency ratios relative to the lowest C; for the diatonic notes the line below that gives the ratios between consecutive diatonic notes. Chromatic notes/ratios in parentheses are less likely to be used in tuning keyboards.
All non-ET systems by definition have small discrepancies. Consider going seven octaves from C1 to C8 on a piano. One can also reach the same key on the keyboard by twelve fifths; but compare the ratios: twelve pure 5°s = (3:2)**12, while seven 8°s = 2**7. A moment’s thought about primes shows that there are no integers A and B such that 3**A = 2**B except the trivial A = B = 0—in other words, a unison. This discrepancy, 3**12 / 2**19 or 531441:524288, is called the Pythagorean comma; it is also the difference between six tones and an 8°. Since pianos use ET, pace stretched octaves, one reaches the same key; but the note reached by going up fifths is really B♯, not C: in principle a slightly higher note.12
Another very important discrepancy is the syntonic comma, with the value 81:80. This was known in antiquity, but became crucial with the rise of JI. It is the difference between the 81:64 PT M3 and the 5:4 M3 of JI. This comma, abbreviated c, will loom large later in this essay. The Pythagorean comma will be abbreviated Pc; references to just “a comma” will mean the syntonic comma.
Intimately tied to discrepancies is the distinction between enharmonic pitches and their frequency order. The chromatic semitone, the apotome, is the difference between a tone and a limma. In PT it exceeds the limma by a Pc. Thus, C♯ is a higher pitch than D♭, and so forth. The situation is reversed in JI: “sharped” notes are flatter than their “flatted” equivalents. This has performance implications: although string students are now taught to adjust intonation to ET at least in some schools, within the last twenty years there were still professional string players who, perhaps unconsciously, preferred PT.13
Because JI tries to accommodate both pure 5°s and M3s, it has two sizes of tones. In the overtone series, C4-D4-E4 are partials 8, 9, and 10 above a fundamental of C2. The C-D tone thus has the ratio 9:8, but the ratio for D-E tone is 10:9. This means that the fifth D-A is a comma flat from 3:2. A corollary problem for PT, JI, and similar systems is the existence of “wolf intervals.” These are out of tune due to a single key having to function for two enharmonic pitches of different frequencies. If one tunes a keyboard with only twelve keys per octave, as one goes ever further in either “the flat or sharp directions” one eventually reaches a key representing two enharmonic pitches that differ by a comma or more. Starting at C, the wall is typically hit at D♯/E♭ or G♯/A♭. If the G♯/A♭ key is tuned as G♯ but the D♯/E♭ key as E♭, then an “A♭ major triad” will actually include not the 5° A♭-E♭ but the very different d6 G♯-E♭.14 Pieces in remote keys (literally, far away along the line—not circle—of 5ths) will sound intolerably bad.
Mean-tone temperament (henceforth, MT) and ET were two solutions. The former took the principle that pure M3s were more desirable for then-current repertoire, and let fifths go slightly impure. The two tone sizes were eliminated by using the number proportionally halfway between four and five—x**2 = (5:4), x=√5/2. MT simply moves the acoustic potholes elsewhere, however. Consider going up by M3s, C-E-G♯-B♯. This yields a ratio for the B♯ of (5:4)**3 = 125:64, which is flat from an 8° by 128:125, called an enharmonic diesis. Theorists and tuners over the centuries spilled much ink computing ways to “spread the pain,” resulting in dozens of temperaments—early music performers can rattle off names such as “Vallotti II,” “Werckmeister III,” “2/7-comma,” and so forth. The standard MT above is formally called “1/4-comma MT,” meaning that all fifths are flat from acoustically pure by 1/4 of a comma.
Players and makers of fretted instruments had a different problem. Since frets must be spaced unequally, if one changes keys they will be wrongly placed relative to each other. Adjusting frets solves this only if one can stop and retune the instrument between every piece—and this is obviously unacceptable for modulating pieces. The obvious solution was ET, which yielded fret placement no better or worse for any key. The problem then of course was how to geometrically construct the twelfth root of two? Vincenzo Gallilei, Galileo’s father, showed that the much simpler 18:17 is a decent approximation.15
For other approaches, one can try to have more keyboard keys per octave. A number of “split-key” keyboards were developed, so that C♯ and D♭ would be separate keys sounding different frequencies. These never caught on, apparently being considered too cumbersome. Multiple microtonal systems have also been proposed: nineteen pitches per octave has been popular, as has 31-note tuning. In one extreme case, a keyboard for playing 53-tone temperament was reported in the English translation of Hermann Helmholtz’s music psychology treatise.16 There is, though, yet another approach, at least for singers.
IIb: Categorical Perception
Cognitive psychology is a vast field. While most of its historical development was dominated by visual research, there has been auditory work going back to Hermann Helmholtz, Theodore Lipps, and Carl Stumpf. One phenomenon across multiple sensory modalities is critical for us: the concept of categorical perception. Simply put, a range of physically distinct stimuli are perceived as belonging to a single cognitive category. Thus, for example, a range of light frequencies are all considered “blue.” Likewise, to any (non-AP) listener, pitches at frequencies 440 Hz, 441 Hz, 439.073 Hz, and so forth, are all “the same.”
The issue of interest in categorical perception is how domain boundaries are defined, and what mechanisms are involved in their crossing. Domains with different tolerance values can interact—in music, the threshold for declaring fifths mistuned is different than for thirds.17 There are also memory limitations. A choir might recognize and correct a mistuned chord but still fail to recognize that during a particular passage it has “returned” to a tonic chord of slightly lower frequency, and so slowly go globally flat. We need not worry about domain threshold fuzziness, but only combating going globally flat or sharp.
I propose to take advantage of categorical perception. The idea is to go past acknowledging that integer-ratio tuning systems have irreconcilabilities, and use categorical perception, via multiple slightly different shades of intervals, to correct errors on the fly.
IIc. A Formal Definition of “Being In Tune.”
We can now formally define being in tune. The intuitive concept is, “Sing/play the pitches of the tuning system without going sharp or flat.” To formalize that, we need to define more formally “pitches of a system.” Here is one possible definition:
Let R be a pitch of arbitrary fixed frequency, and O be the fixed pitch an acoustically pure octave higher. A standard tuning system is: 1) a set of N+1 pitches consisting of R, O, and N-1 additional fixed pitches with frequencies between R’s and O’s that collectively partition the R-O octave into N intervals; and 2) pitches whose frequencies are outside the referent 8ve belong to the system if and only if their frequencies are related to frequencies of pitches in the R-O octave by some power of two.18
This definition is completely generic: there are absolutely no restrictions on the frequencies of the pitches within the referent octave. It is merely that given a pitch of the system in the referent octave with frequency f, the pitches at frequencies 1/2f, 2f, ad infinitum are also members of the system. Thus, JI, 1/4-c MT, Javanese slendro, and a scale containing seventy-three pitches with spacings determined by rolling Dungeons & Dragons™ dice are equally legitimate. Note that aesthetic tolerance is a different matter!
The qualifier “fixed” immediately limits a standard tuning system to pitches which frequencies are derivable from the defining table/algorithm. It excludes a pitch being able to vary within the bounds of categorical perception. That is, if one has defined one’s system as the usual 12-ET with the pitch at 440 Hz a member of it, the pitch at 439 Hz is not a member. Thus, being in tune is formally definable as:
Given a tuning system S, a performance of a piece is in tune with respect to S if and only if 1) all pitches performed have frequencies in S, and 2) intervals between pitches always correspond to intervals in S’s referent octave (or with one or more added octaves).19
So for a performance to be in tune with respect to PT, all M2s must have 9:8 ratios, all As must be the same frequencies as the referent A or some octave of it, and so forth. Note that this definition is not limited to the standard tuning systems defined above; I am about to introduce an extension.20 My definition is but one way to define “a tuning system,” and is arguably far too limiting. It does, though, give us a working basis.
We can return now to the Prophetiae Prologue and Klumpenhouwer’s analysis. He posits an idealized, automated choir singing only JI intervals, using a description from Descartes’ Compendium musicae, and applies it to the Prologue. He concludes that the final G3 must necessarily be flat relative to the first by three commas, and that eight of the piece’s fifty-four chords—ignoring a few ornaments—must perforce be mistuned (although he only lists six chords in his text).21 He then uses his runtime data to critique Mitchell’s and Berger’s analyses, and to point out some interesting structural details of the Prologue.
His Cartesian analysis has a problem, however. It ignores a reality already recognized by Renaissance theorists: performers use more than a single shading for various intervals. Zarlino, for example, clearly distinguishes the two sizes of tones and semitones and directs a fair bit of attention to them,22 notes that vocalists do in practice shade tunings,23 and in fact demands that composers consciously use the two sizes of tones/semitones in order to allow consecutive imperfect consonances.24 The principle was already known to Gaffurius forty years earlier: he argues that thirds and sixths can be adjusted by a comma to improve concords.25 Such intervallic distinctions are still important to Rameau and Kirnberger, and bear on theoretical issues into the nineteenth century—Viennese theorists still preferred JI as late as the time of Sechter.26 The question is, can one use extra shadings to correct comma errors to avoid going flat or sharp while keeping sonorities justly-tuned? I term a system with multiple interval shadings an extended just intonation.
There is potential confusion here. As used by composer Ben Johnston and others, extended JI refers to systems that use powers of primes beyond five: not only 7-limit JI, but 11-limit, and so forth.27 I personally feel that a better name for such JI systems is “higher-limit JIs.” (More whimsically, one could say “higher-octane JIs.”) In contrast, I am proposing a 5-limit JI extended by having multiple, slightly different shadings for certain pitches in the scale, utilizing categorical perception.28 I will hence refer only to my system, using the acronym “XJI,” and ignore the systems of Johnston and others.
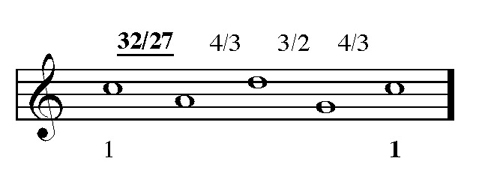
Above I noted that even a simple diatonic melody can get out of tune quickly in JI; the existence of powers of five in JI ratios, besides comma discrepancies already in 3-limit PT, exacerbates the situation. Here is an example of my XJI in practice. The snippet in Figure 2a ends with the final C a comma flatter than the first one; the “error” occurs because the descending m3 to A divides the initial C’s frequency by 6:5. The power of five never gets canceled out anywhere, while the powers of two and three in the 4°s and 5°s do cancel. Choral directors, however, know that descending intervals are prime places for choirs to go flat; and any chorister knows all about being harangued to “Think high!” when singing them. Suppose that one sings not a JI m3 but the smaller PT 32:27 m3. Now there is no power of five, and the bookkeeping works out, as in Figure 2b.29
Figure 2a. JI diatonic melody going flat.
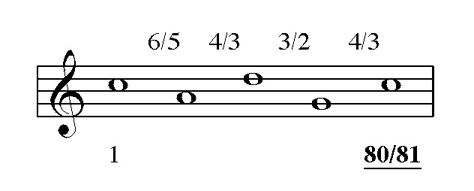
Figure 2b. Melody with comma correction.
My XJI is thus an example of “adaptive tuning.” That is, there is some reference standard that a system (computer algorithm, singer, etc.) understands it should return to, and chooses from a set of pitch alternatives to correct itself when any momentary chord or pitch would deviate from the standard. I am arguing that historically, this is the choir trained to “Think high!” when singing descending intervals.
Complications easily arise in multi-voice textures, as seen in this four-voice example (see Figures 3a-b). Between chords one and two, the power of five in the tenor E (5:2) above the bass C cancels when the E moves by a JI diatonic semitone (16:15) up to F (8:3). The alto A above the bass F has another power of five, but now there is no semitone to cancel it. If the A is rearticulated as in Figure 3a, the altos can adjust it up a comma at the revoicing (“Think brighter here, altos!”), which does cancel it. If, however, the A is tied over, there is no way out (Figure 3b), resulting in a short fifth D-A and a mistuned D triad.
Figure 3a. Four-voice texture with revoicing. Figure 3b. Four-voice texture with tie.

This is in essence a reinventing of a wheel. A couple of years before I gave the original (extremely different) conference version of this essay, Richard Ashley had proposed essentially the same idea for synthesizer use. Shortly after that presentation an essay by Jonathan Walker appeared, also using my conception of XJI (although he did not so label it). I did not become aware of either of those until some years later. Walker’s analysis of Josquin, however, uses a more limited number of pitches a comma off standard JI values; and he applies the concept only to nonchromatic works such as Josquin motets, and does not consider applying the technique to later repertoires as done herein.30
We can now expand the formal definition above of tuning system for XJI and equivalent systems. We retain the “N-1 additional fixed pitches with frequencies between R’s and O’s” clause, but add “grouped into M conceptual categories (with possibly unequal membership sizes), where M < N, such that a) the average interval size between members of a category is significantly smaller than the interval size between the centers (i.e., arithmetic mean frequencies) of different categories; and b) categories may be optionally subdivided into ‘enharmonic subcategories’ within which membership may overlap.” In other words, while we still have M “conceptual notes” in the octave, (1) each conceptual note is a cluster of distinct fixed frequencies that within the limits of categorical perception sound the same, (2) the frequency differences between the centers of clusters are much larger than those between intra-cluster members, and (3) for musical convenience we can subdivide a cluster into enharmonic subgroups with possibly interlaced members. Thus, “C♯/D♭” is a single conceptual note “a semitone” higher than “C” and lower than “D” that contains some number of fixed pitches, some of which we assign to the enharmonic subcategory “C♯” and the rest to “D♭”—in particular, the JI diatonic ST 16:15 is assigned to D♭, the 135:128 difference between a 9:8 tone and it is assigned to C♯, and the pitches +/- one comma from each of them are also assigned to those respective designations (see Table 2). There is no reason to forbid conceptual notes like “Dx/E/F♭,” but those are not needed for the Prologue. Enharmonic subcategories for “the black keys” are sufficient. Since conceptual note categories have multiple members, an interval between categories is in tune as long as its frequency ratio corresponds to some pair of members, one from each category—both 5:4 and 81:64 are in-tune major thirds here.
III. Analysis of the Prologue
We can now attempt a formal operational definition of the problem, with three criteria. Is there a sequence of XJI melodic intervals for all parts in the Prophetiae Prologue such that (1) a starting reference pitch-class will always recur at the same frequency or powers of two times it (i.e., the referent never goes sharp or flat and its octave duplications are always acoustically pure); (2) vertical sonorities are always justly tuned (i.e., the chord members are in tune with respect to each other vis-à-vis standard JI, even if their pitches are off standard JI values relative to the referent); and (3) successive melodic intervals within parts are acoustically pure as much as possible (in particular, fifths and fourths should be pure if at all possible)? These criteria may seem rigorous, but there is still a trap—left in to show the need for complete clarity of thought in such matters. Assuming a referent of C, if chord members are “in tune with respect to each other vis-à-vis standard JI” then how do we treat cases like the D-F-A triad? All three JI major triads have the same 4:5:6 ratio makeup in ascending order and the minor triads on E and A likewise are both 10:12:15; but D-A is a comma flat. Remember, that short fifth is not an error—it is a product of the definition of JI. So, “being in tune” could be contradictory by definition: if the concept is stated only as “sing the frequencies of the system,” but intuitively we also have constraints that “chords in the system must have such-and-such specific intervallic structures,” and “melodic intervals must have such-and-such frequency ratios,” they may not all be satisfiable for any piece.
Indeed, some readers likely have wondered about this vis-à-vis Figures 2a-3b since I formally defined being in tune. Figure 2a was the classic example of JI’s inability to avoid going flat/sharp; but if one simply sings the A-D fourth a comma wider than 4:3, as exists in standard JI, it works out fine. The penultimate sentence in paragraph two of this paper is thus unmasked as mystery-story misdirection due to implicit assumptions during casual perusal.31
D-F♯-A will sound more unacceptable than D-F-A if we keep the short D-A fifth; and we will see other triads with chromatic notes. We can reword criterion 2 to retain its intuitive spirit as follows: “vertical sonorities are always tuned so that if rearranged to closest-spacing root-position the chord members of major triads will have frequency ratios in 4:5:6 proportion with each other, and the chord members of minor triads will equivalently be in 10:12:15 proportion, even if their pitches are off standard JI values relative to the referent.” With this last point, formal rigor is no longer needed.
The three goals obviously conflict. The first two are essential; goal number 3, tuning melodic intervals to standard JI, has to be relinquished at times. Our fixed-frequency, goal number 1, however, refers only to a single referent pitch-class. The frequencies of other pitch-classes relative to it will have to float, as did the As in Figures 2b-3a. We hope to minimize fluctuations—especially if possible to hold steady pitch-classes a fifth above or below the referent—but as we go farther out along the line of fifths we must be flexible.
Recall Klumpenhouwer’s conclusion: a choir singing the Prologue in non-XJI necessarily ends up three commas flat and with eight chords out of tune. We can do much better. He also presents data in cents, but that is both anachronistic and—since he unfortunately gives no table showing in- and out-of tune cent-values—nigh unreadable. The analysis will thus use integer ratios as in the prior examples. Table 2 shows a set of XJI ratios and abbreviations, including unused shadings for completeness; discussion will use the abbreviations. Not surprisingly, there are many semitone inflections.
Table 2. Complete Set of Extended Just Intonation Ratios for Referent = C.
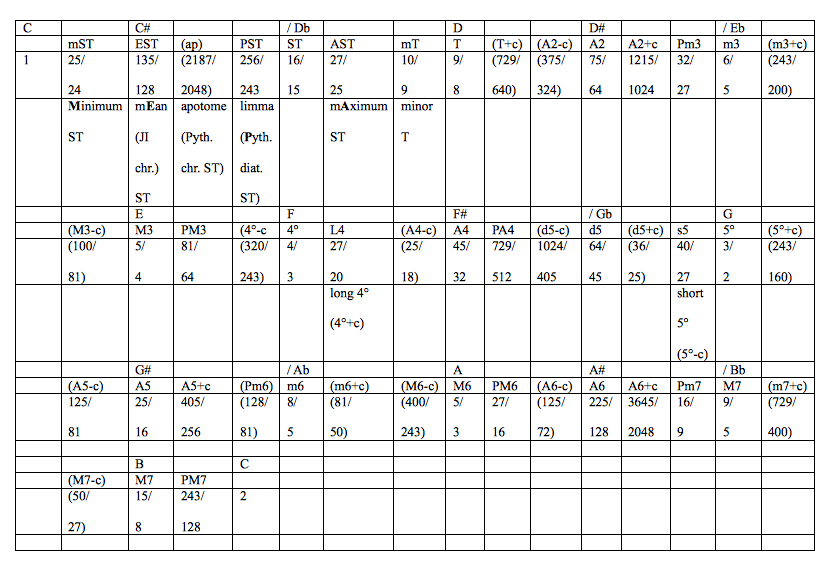
Note: This shows ratios for all 5-limit JI pitches plus shadings +/- one comma; values not used in the analyses are in parentheses. “P” = “Pythagorean.” Semitone shadings are interleaved; in increasing order they are: mST, PST, EST, ST, ap, AST. Some interleavings also occur between unused larger intervals.
The Prologue begins on a tenor G and ends on a G-chord. This argues for making G our fixed referent; but the choice is arbitrary. Since C is “the default pitch-class” nowadays and tuning tables are given in reference to C, I will declare the initial bassus C3 as our referent. That is, it has an analytical value of one, whatever its frequency. All other Cs must be some power of two above it. In the analytical figures, lack of annotations for pitches or intervals indicate standard JI values (as in Table 1) in force. Where XJI melodic intervals are needed, their abbreviations from Table 2 are shown between notes, and pitches a comma off standard JI values have such indicated above them. A few extra values and abbreviations are indicated for clarity.
The piece divides into three sections, with cadences at measures 9, 18, and 25, on G, C, and G. Given our use of C as referent, though, the computational reference point of the cadence in measure 9 will be on the C-chord later in the measure, and the C-chord in measure 24 will also be a computational point. There is thus an additional “internal cadence” for computational purposes on the C chord at the end of measure 6.
Independent of major/minor distinctions, chords are built on pitches along the line of fifths from E♭ to G♯. Klumpenhouwer says (p. 25) that chords with second-related roots cause the tuning problems. While we see a few instances of this, chords with third-related roots are more problematic due to the powers of five involved. To the extent that the following criteria are met, we can avoid most comma difficulties: (1) Don’t mix “flat keys” with “sharp keys;” this includes mode mixtures such as c and D in the equivalent of a g-minor iv-V-I progression. (2) Don’t have sustained common tones across chord changes where the root moves in third relations (e.g., B♭-D or A-f ♯). In measures 1-6 (see Figure 4) this mostly happens, and there are almost no problems.
Figure 4. Measures 1-6 reduction.

Our first decision point is the B-c♯ progression at measures 3-4. The c♯ is Klumpenhouwer’s first perforce-mistuned chord, but there are two ways to fix it. Does the tenor sing a 5° F♯-C♯, resulting in C♯s sharp by a comma (the first version, set off by double bars in lieu of parentheses), or a s5 to avoid that (in which case the cantus D♯-E needs to be an AST and the bassus B-C♯ a mT)? If the former, the Es in the cantus in the c♯-chord and altus in the following E-chord will differ by a comma. The altus can correct by singing a Pm6 so both are possible; but then could not get its E from the cantus.32 Since the F♯-C♯ fifth is quite far from the referent, it seems simpler to keep both Es at standard JI and use the s5/mT/AST option. In measure 5 we again have a second-related progression, E-f♯: Klumpenhouwer’s next mistuned chord. To avoid this, the cantus/altus/tenor respectively need to use an AST/Pm3/mT; but the progression f♯-D6-G-C, a fairly chromatic motion, ends up with only the As sharp a comma (i.e., up to PT values).
Figure 5. Measures 7-12.

The next problem is that Lasso moves into the “flat keys” in measure 7 then flips from B♭ to the “sharp key” D in measure 8, as seen in the first part of Figure 5. For the measure 7 bassus F-B♭ to be a 5°, the altus D goes a comma flat. Then, to tune justly (i.e., triad in 4:5:6) the first measure 8 D chord, the lower three voices sing non-XJI intervals and the cantus sings an mST. Working back from the measure 9 C cadence we find that the first D-chord is a comma flat from the second one. The latter is mistuned for Klumpenhouwer. We sidestep the error by having the choir enter the c6 chord by AST/mT but leave by ST/T; since this makes the tenor A in the second D-chord a comma sharp, it sings an mT to the following B.
The first version of measures10-12 shows a hypothetical continuation after the measure 9 C cadence. It begins with 3rd-related chords (C-E) that involve voice-crossings. If the choir simply sings JI intervals, the measure 12 G-chord will be a comma flat—just as we approach the hardest section. We could try to concede a flat G-chord as does Klumpenhouwer, despite having hoped to keep all Gs and Fs a 5° away from our referent C. However, due to the held notes in the cantus and tenor in measure 13, we could not get back on track by having the bassus descend a Pm3 to its E. There is a solution, though: have all the voices shift in measure 10 using PT intervals, as in the final section of Figure 5. The nature of the text and the rhythmic texture that Lasso uses here permit him to get away with this. He has just had a caesura at the “real cadence” on the G-chord, and now he announces in long block chords, “Haec sunt:” “These are!”
Figure 6a. Measures 13-18 reduction.

Figures 6b-6d. Measures 13-15 solutions.

The most difficult section is measures 13-18 (see Figure 6a). Going backwards from the C-chord in the measure 18 cadence, there is a line of 5ths progression C-G-D-A-E, with the E-chord being embellished as (reading forward) E-g♯-E6. The problem is that all the chords from the G back have pitches tied across chord changes—the tenor D between measures 16-17, the altus E between measures 15-16 and its measure 16 A, and the measure 15 cantus G♯. We have the situation of Figure 3b. Computing with just the bassus, the Es in measure 15 have to be a comma sharper than the Es in measure 13, as noted on Figure 6a. If the measure 16 altus A on “ca,” embellished by a lower neighbor G (omitted in the reduction), had not been tied across the A-D chord change, the bassus could have used the s5 D-A of standard JI and the altus revoice to correct the comma; but that is not possible.
We have four options:
(1) We could admit defeat and go forward with the values from measure 13. Everything from measure 16 on would be at least one comma flat. In Klumpenhouwer’s terminology, measure 16 would be a “structural comma-drop.”
(2) We could have the E6-chord at the end of measure 15 be out of tune either by (a) having an L4 between the altus and tenor or (b) by having the G♯s in cantus and bassus be a comma flat.
(3) We can have both the E- and E6-chords in measure 15 with respect to themselves, with their Es a comma sharp relative to the C3 referent, and fix the problem in measure 14. The bassus must then sing either a B-E L4 or an F♯-B s5, with one upper part revoicing by a c and another moving an AST. Those solutions are shown in Figures 6b-c respectively.
(4) We can let the bassus keep singing 5°s and work backwards with everything sharp a comma until the beginning of measure 14, then make the correction across the second-related e-F♯ chord change.
As seen in Figure 6d, the last option is not pretty. The altus in particular has to sing an extremely unusual and difficult interval. Recall from Figure 2a that singing a descending JI m3 would leave it a comma flat, but since in this scenario the pitches of the F♯-chord are a comma sharp, the altus must shave two commas off its descent. Even though all chords stay justly-tuned this transition may well sound rather bad, particularly since measures 13-14 are, to use modern terms, simply a iv-V-I progression in B major. Furthermore, unlike the measures 9-10 “haec sunt” there is nothing in the text underlay or texture here to mitigate such a mistuned transition. On the other hand, the chord shift is far away along the line of fifths, so perhaps we should not be surprised by such a dilemma—note that the Prologue’s only A♯ occurs here. In any case, someone preparing the work must make a judgment call on which solution is the least problematic. Due to the minims in the cantus/tenor and the F♯- and B-chords being locally farthest from C, I personally would have the choir correct things between them.
Figure 7. Measures 18-25.

In the last section (see Figure 7), the bassus in measures 18-21 looks regrettably familiar, as it is closely related to Figure 2a. Now, though, we have four parts to juggle. Fortunately, Lasso has set this passage homophonically with all notes rearticulated, so we can correct commas as needed. The only casualty here is that the altus G in the E♭-chord in measure 19 must be a comma flat. Without that, all four parts would have to drop a comma between the two B♭ chords on “pi-do” across measures 19-20, a noticeable “Huh??” moment—and the altus F in the first of those would itself be sharp a comma. Slipping in comma revoicings during various third-related chord pairs (F-D in measures 18-19; G-E♭ in measure 19, with the flat G; and G-E in measures 20-21) is clearly far preferable. The G-chord of measure 20 and the F-chord in measure 22 are mistuned for Klumpenhouwer; but here, judicious use of mT/Pm3 as needed while entering or leaving them keeps them justly tuned.
In the final measure the cantus must end with a s5 A-D. This problem is unavoidable even in just a two-voice cantus/bassus framework. Since the D-A s5 is already in standard JI, that does not seem onerous.
To sum up, by using XJI we are able to keep all Cs and all basic sonorities in tune; and only three melodic fifths are not pure. Furthermore, one of the s5s is the standard JI D-A (so that all Gs and Fs except the measure 19 altus G are 5°s relative to C); and had we decided to make the altus do more work in measure 4, the preceding tenor F♯-C♯ could also have been pure.
IV. Two Nineteenth-Century Cases
Lest it be thought that this sort of analysis is useful only for late Renaissance chromatic music, let us briefly look at one of the standard nineteenth century choral a cappella pieces, Bruckner’s Locus iste. The two chromatic sections of interest here are the sequence in the middle section, measures 21-26, and the melisma on “Deo” in measures 40-42, shown in Figures 8a-b. The piece overall is in C, so we again use C as the referent pitch to occur at powers of two.
Figure 8a. “Locus iste,” measures 21-26.

Figure 8b. “Locus iste,” measures 40-42 (with pickup).

As shown in Figure 9a, the sequence can be sung justly with the tenors singing diatonically, as long as the altos rearticulate the D down by a comma between measures 23-24, and the tenors use an AST for their B♭-A. This also allows the melodic intervals in all three parts to be exact analogues during the sequence. The alternative, with the altos holding the D constant and the other parts computed relative to them, is inferior: either all three parts have to retune across the suspension—hardly pleasing—or the A-f6 transition has to involve ESTs in the lower voices and a PST in the soprano. Clearly, the preferable place for adjusting anything is between statements of the sequence elements, right after the measure 23 g6 chord.
Figure 9a. Sequence reduction.

The melisma is the problem, because so many parts are tied across chord changes (Figure 9b). If the g-chord in measure 40 is in tune, then the series of tied notes [alto B♭/bass D/tenor A] means that by the second half of measure 41 either the alto C will have to be sharp a comma, or the penultimate three chords before the cadence will be mistuned. In the D7-chord alone, having the C be flat relative to the triad might be acceptable—it will be the essential dissonance, in Kirnberger’s term—but both it and the A are tied through the next two chords, and this would mean that the triad portion of the half-diminished chord on the downbeat of measure 42 would be mistuned. Correcting the comma into the final e chord is possible, as shown in the figure; but since there is a grand pause right after, it is easier and aesthetically preferable to let things stay sharp a comma and reset intonation when the choir reenters in measure 44. Nonetheless, there is no perfect solution for this passage. We must choose between mistuned chords or going sharp.
Figure 9b. Melisma reduction.

What is the limit of applicability of this sort of analysis? Certainly it would be ludicrous for a piano piece by Milton Babbitt. Remember, however, that studies (see Endnote 13) have shown a preference by string players for PT over ET—this has important implications for atonal analysis, since it invalidates the assumption that enharmonic spellings in such music are always equivalent. Meanwhile, let us examine one last familiar nineteenth century excerpt, shown in analytic reduction in Figure 10.
Figure 10. Reduction of Tristan Prelude start.

If anything in common-practice era music is non-diatonic, it is the opening measures of Tristan und Isolde. Taking A as the referent pitch, with the initial A3 set at 2 to simplify the fractions, the analysis shows that even this snippet can be done in XJI. The measure 3 D can be tuned two ways, depending if one wants the final Mm7 chord analogous to C-E-G-B♭ or G-B-D-F in standard JI. There are also two choices for the passing A# as one prefers for emotional affect—the interval with the D will be one of the three flavors of A5.
V. Conclusion
What have we accomplished besides a workout for fifth-grade math skills? It certainly helps composers regain an awareness of compositional subtleties. The analyses show that when certain compositional restrictions are adhered to and additional intervals already used in practice by choirs are recognized theoretically, it is possible to write very striking chromatic music that can be sung entirely in (X)JI without going flat or out of tune.
It is also important for performers. We were able to identify several problem spots. For some of them, such as the measure 9 chord shift, we found solutions that would forestall a choir from going globally flat by the end of a performance. In the Bruckner excerpt, we determined that the melisma a priori cannot be entirely in tune, or that one or more voices must sing out-of-tune melodic intervals in order to stay in tune relative to the other parts. For a choir director looking to perform such pieces, this type of information must be part of their preparation.
Granted, such analysis may have little practical significance in most cases. After all, most choirs will have many more problems with the Prophetiae Prologue than those noted—how many choirs have every member able to adjust pitch by one Hz. on demand? It does, however, give one the theoretical intonational limits, the musical analogue to the quantum mechanical limits of measurement precision. It also tells a choir director where he or she has to accept a slightly out-of-tune chord. In the more realistic case where the director, not the entire choir, has perfect pitch, they will know not to waste rehearsal time on that chord, or where else they might have to work things slightly differently.
There is one final objection to this type of analysis, whose power derives from turning the argument of historical performance practice into ammunition. When Lasso wrote the Prophetiae cycle performers were far more likely to use some type of MT rather than JI, and near-ET had triumphed by the time of Locus iste. In his survey of tuning systems Murray Barbour notes:
[T]his music was not ordinarily sung unaccompanied in the sixteenth century. A cappella meant simply the absence of independent accompaniment, not of all accompaniment.33
Recall the Prologue’s sonority-root range, E♭ to G♯. This is exactly the typical tuning range for 1/4-c MT keyboards based on C. Given these, maybe we should reconsider the Prologue analysis using MT. I will not present such—readers perhaps already uneasy about keeping straight so many integer ratios would surely be unnerved at repeating the process with sundry roots of five littering the page—but will say that all the problem spots entirely resolve themselves when performed in 1/4-c MT tuned relative to C.
We appear to have a “smoking gun” favoring MT, and the analysis here may now seem superfluous. Various writers have argued in favor of MT. Barbour claims that JI has never been more than a theoretical construct; Mark Lindley and Ronald Turner-Smith note that practice apparently morphed from PT through a transitional scheme they term “quasi-Pythagorean” to MT systems; and Donald Hall’s goodness-of-fit analysis indicates something approaching 1/4-c MT is optimal for Western music from the thirteenth to eighteenth centuries.34 Yet, Zarlino’s and Gaffurius’ statements on singers’ variable tuning read like references to actual practice. Also, arguments by other writers that a new solution was needed because singers trying to sing in tune keep necessarily going flat to support the idea that JI was really used on at least some occasions. We can never know how Zarlino’s singers adjusted tuning; but as noted, psychoacoustical studies indicate that modern singers tend to prefer JI even though their ears are saturated by ET music.
What can we make out of this? First, this principle remains valid for any non-ET system. If one believes a piece should be done in 1/4-c or some other MT to be historically accurate, then analyze the piece in such and locate the problems. Second, since a modern unaccompanied choral performance necessarily uses modern singers, one can be practical and accept that some variant of JI, likely with the extensions noted herein, will happen—in such a case, this type of analysis is again useful to find theoretical problem spots. Finally, one can argue that tuning preferences are a matter of artistic choice and that the resulting emotional affect is the real criterion by which to judge any particular performance. Perhaps in the end this type of analysis finds its best use by re-illuminating aspects of the subtle richness of music for us all.
Author Note
I am deeply grateful to Kirin Nielsen, Christine Amos Linial, Timothy Chenette, Robert Hasegawa, and David Thurmaier for a variety of extremely helpful and insightful comments on the penultimate draft of this paper, after it had an extremely lengthy gestation due to a multiplicity of circumstances. I am also indebted to Caleb Mutch for bringing the Gaffurius citation to my attention, in his presentation at the Society for Music Theory’s 2011 national conference in Minneapolis.
Bibliography
Ashley, Richard D. “Modeling Ensemble Performance: Dynamic Just Intonation,” in Proceedings of the International Computer Music Conference, 1992, 38-41. San Francisco, CA: Computer Music Association.
Barbour, J. Murray. Tuning and Temperament: A Historical Survey. East Lansing: Michigan State University Press, 1951.
Berger, Karol. “The Common and the Unusual Steps of Music Ficta: A Background for the Gamut of Orlando di Lasso’s Prophetiae Sibyllarum.” Revue Belge de musicologie 39‒40 (1985‒86): 61‒73.
_____. “Tonality and Atonality in the Prologue to Orlando di Lasso’s Prophetiae Sibyllarum: Some Methodological Problems in Analysis of Sixteenth-Century Music.” Musical Quarterly 66 (1980): 484‒504.
Bergquist, Peter. “The Poems of Orlando di Lasso’s Prophetiae Sibyllarum and Their Sources.” Journal of the American Musicological Society 32 (1979): 516‒38.
Boetticher, Wolfgang. Orlando di Lasso und seiner Zeit. Kassel: Bärenreiter, 1958.
Chenette, Timothy. “The Contrapuntal Correctness of Lasso’s Prologue to the Prophetiae Sibyllarum.” Presentation at the Society for Music Theory meeting, Minneapolis, MN, Oct. 27‒30, 2011.
Davison, Archibald T., and Willi Apel, eds. Historical Anthology of Music, vol. 1. Cambridge: Harvard University Press, 1946.
Devaney, Johanna, Jonathan Wild, Peter Schubert, and Ichiro Fujinaga. “How Do Singers Tune?” Presentation at the Society for Music Perception and Cognition meeting, Rochester, NY, Aug. 11‒14, 2011.
Fonville, John. “Ben Johnston’s Extended Just Intonation: A Guide for Interpreters.” Perspectives of New Music 29, no. 2 (1991): 106‒37.
Gaffurius, Franchinus. De harmonia musicorum instrumentorum opus, translated by Clement A. Miller. Musicological Studies & Documents 33. N.p.: American Institute of Musicology, 1977.
Groven, Eivind. “My Untempered Organ.” Organ Institute Quarterly 5, no. 3 (1955), 37–40.
Hall, Donald E. “Quantitative Evaluation of Musical Scale Tunings.” American Journal of Physics 42 (1974): 543‒52.
Harvey, Jonathan. “A Beginner’s Guide to Prophecy: Orlande de Lassus’ Prophetiae Sibyllarum.” Choral Journal 50, no. 11 (2010): 8‒17.
Keislar, Douglas. “History and Principles of Microtonal Keyboards.” Computer Music Journal 11, no. 1 (1987): 18‒28.
Kirck, George T. “Computer Realization of Extended Just Intonation Compositions.” Computer Music Journal 11, no. 1 (1987): 69‒75.
Kirnberger, Johann Philipp. The Art of Strict Musical Composition. Translated by David Beach and Jürgen Thym. New Haven, CT: Yale University Press, 1982.
Klumpenhouwer, Henry. “The Cartesian Choir.” Music Theory Spectrum 14 (1992): 15‒37.
Lake, William. “Orlando di Lasso’s Prologue to Prophetiae Sibyllarum: A Comparison of Analytic Approaches.” In Theory Only 11, no. 7‒8 (1991): 1‒19.
Lindley, Mark. Lutes, Viols, and Temperaments. Cambridge: Cambridge University Press, 1984.
Lindley, Mark, and Ronald Turner-Smith. Mathematical Models of Musical Scales: A New Approach. Bonn: Verlag für systematische Musikwissenschaft, 1993.
Lloyd, Llewelyn S., and Hugh Boyle. Intervals, Scales and Temperaments. 2nd ed. New York: St. Martin’s Press, 1978.
Loosen, Franz. “Tuning of Diatonic Scales by Violinists, Pianists, and Nonmusicians.” Perception and Psychophysics 56 (1994): 221‒26.
Lowinsky, Edward. Tonality and Atonality in Sixteenth-Century Music. Berkeley: University of California Press, 1961.
Mitchell, William. “The Prologue to Orlando di Lasso’s Prophetiae Sibyllarum.” Music Forum 2 (1970): 264-73.
Rameau, Jean-Philippe. Treatise on Harmony. Translated by Philip Gossett. New York: Dover, 1971.
Richardson, Lewis F. “Atmospheric Diffusion shown on a Distance-Neighbor Graph.” Proceedings of the Royal Society A, vol. 110 (1926): 707‒37.
Samplaski, Art. “Response to Paul F. Zweifel.” Communications, Indiana Theory Review 17, no. 1 (1996), 119-123
Sethares, William A. Tuning, Timbre, Spectrum, Scale. 2nd ed. London: Springer, 2005.
Teo, Kian Seng. “Lassus’s Recueil du mellange: Its Influence on Chromaticism in England.” Music Review 48‒49 (1988): 102‒13.
_____. “Three Continental Chromatic Compositions in Mid-Sixteenth Century England.” Music Review 46 (1985): 1‒11.
Vos, Joos. “Purity Ratings of Tempered Fifths and Major Thirds.” Music Perception 3 (1986): 221‒58.
Walker, Jonathan. “Intonational Injustice: A Defense of Just Intonation in the Performance of Renaissance Polyphony.” Music Theory Online, 2, no. 6 (1996). <http://smtmto.org/mto/issues/mto.96.2.6.walker.html>, verified 23 June 2011.
Wason, Robert. Viennese Harmonic Theory from Albrechtsberger to Schenker and Schoenberg. Ann Arbor, MI: UMI Research Press, 1985.
Zarlino, Gioseffo. On the Art of Counterpoint. Translated by Guy A. Marco and Claude V. Palisca. New Haven, CT: Yale University Press, 1968.
Zweifel, Paul F. “Just Tuning and the Unavoidable Discrepancies.” Indiana Theory Review 15 no. 2 (1994), 89-120.
Endnotes
1Richardson, “Atmospheric Diffusion,” 707.
2Lloyd and Boyle, Intervals, Scales and Temperaments, is a simple introduction; Barbour, Tuning and Temperament, remains the standard treatment.
3Davison and Apel, Historical Anthology, item #174.
4According to Mitchell, “The Prologue,” Lasso’s editorial practice was that accidentals applied only to the note immediately following; and indeed, the partbooks contain accidentals for each of several series of repeated notes (reflected in the transcription). Some transcriptions give a ficta for the measure 24 tenor F but I believe, based on the care in the partbooks, that F-natural is intended. The translation is from Berquist, “The Poems.”
5Teo, “Three Continental Chromatic Compositions,” and “Lassus’s Recueil du mellange.”
6Harvey, “Beginner’s Guide,” is a simple introduction. The composition’s dating is given in Bergquist, “The Poems.” Lake, “Lasso’s Prologue,” begins with some biographical background. See also Boetticher, Orlando di Lasso.
7Lowinsky, Tonality and Atonality, 39‒41.
8Berger, “Common and Unusual Steps.”
9Mitchell, “The Prologue.” Chenette, “Contrapuntal Correctness,” argues that much of the chromaticism is explainable as cascading solutions to avoid tritones, following sixteenth century rules of counterpoint.
10Berger, “Common and Unusual Steps”; Berger, “Tonality and Atonality”; Lake, “Lasso’s Prologue”; and Klumpenhouwer, “Cartesian Choir.” Lake briefly discusses writers prior to him.
11Because the analysis section will abbreviate “Pythagorean” as “P,” to forestall confusion the acoustically pure perfect consonances are denoted by “5°,” etc. Generic mention of “a fifth” indicates an interval not necessarily a pure 3:2, and so forth.
12This demonstration can be done in only three or four minutes. Going through it drives home the point that “Spelling matters!” and would do much to cut down on student complaints on that front.
13Loosen, “Diatonic Scales,” is representative. Devaney et al., “How do Singers Tune?” suggest additional subtleties, though.
14The JI d6 is 192:125, larger than a 5° by 128:125—nearly an ET quarter-tone.
15The result goes flat by just under a quarter-tone over four octaves, well beyond the needs of Renaissance and Baroque performers. A sample Renaissance diagram for placement of lute frets is in Lindley, Lutes, Viols, 26. He also notes (5; 21) that due to considerations of variable tension as one presses the string to a fret, intonation varies from strict ET. Placing frets in 18:17 approximations actually yields better ET results than placing frets at the exact twelfth-root points.
16Keislar, “History and Principles.”
18The definition is worded to exclude various systems that are not octave-based and thus not germane.
19Vibrato is being ignored. While it may be physically impossible to eliminate it completely, some singers (particularly early music specialists) can reduce it to where it can be ignored for practical purposes. Singers are thus assumed to be vibrato-less.
20An excellent, far more rigorous yet more general formalization—which allows incorporating vibrato, and so forth, in the definition of “a pitch”—is in Lindley and Turner-Smith, Mathematical Models.
21The inherently mistuned chords in his p. 27 diagram are #s 4, 6, 7, 13, 23, 41, 46, and 54. These are respectively on the syllables “ma” in measure 4, “quae-aud” (the chord is revoiced) in measures 5‒6, “di” in measure 6, the suspension on “no” in measure 8, “trae” in measure 14, “ne” in measure 20, “runt” in measure 22, and the final “lae.” His p. 25 list omits #s 7 and 46.
22Zarlino, Counterpoint, 36‒38.
23Ibid., 35: “[Voices] can tune intervals higher or lower as desired and through this bring to perfection any composition.” Seemingly contradictory material is nearby; but a discussion is beyond this essay.
24Ibid., 62ff. Zarlino also discusses two species, i.e., orders of tones and semitones, of minor thirds on pp. 32‒33. He says, “its ratio remains constant throughout the gamut.” However, the examples in the translation—D–F and E–G—are respectively the PT 32:27 and the usual JI 6:5.
25Gaffurius, De harmonia, 143: “Thus you see that the power of 81:80 in the tempered alteration of such skillfully joined intervals is so great that it is possible to influence the major 3rd and major 6th by the removal of 81:80, and likewise the minor 3rd and minor 6th by their increase in sound and size by the addition of 81:80...”
26Rameau, Harmony, 27‒40; Kirnberger, Strict Musical Composition, Ch. 1, esp. 20‒24; Wason, Viennese Harmonic Theory, 34 and 154n15.
27A good introduction is Fonville, “Johnston’s Extended Just Intonation.” Kirck, “Computer Realization,” is an early discussion on implementing Johnston’s system.
28Johnston does employ notes separated by a comma, and even includes notation (+, –) for them: thus, “C+” is the pitch a comma higher than C. He also includes other shadings that sharpen or flatten JI pitches by higher-limit commas, with different symbols for them. Crucially, these are different pitches for him. In contrast, I consider a note raised or lowered a comma still to be cognitively “the same pitch” as the unaltered version; and I only use as many additional shadings as necessary on a per-piece basis.
29The pitch sequence in Figure 2a was presented in Zweifel, “Unavoidable Discrepancies,” although it had been known for centuries. Figures 2b through 3b are taken from Samplaski, “Response,” a precursor to the original version of the present essay.
30Ashley, “Modeling Ensemble Performance”; Walker, “Intonational Injustice.” Ashley’s proposal was greatly expanded upon in Sethares, Tuning, Timbre, which is now the standard work on the subject. Decades earlier, however, Eivind Groven had constructed an electro-mechanical organ, detailed in Groven, “My Untermpered Organ,” that implemented a form of my XJI. Each pitch occurred in three versions, separated by a comma; and depending on the most recent chord played, sets of relays determined which versions of each pitch could sound next.
31In a sense, then, standard JI is already extended: it has two shadings each for semitones (B‒C and C‒C#), tones (C‒D and D‒E), and minor thirds (E‒G and F#‒A/D‒F), plus the short fifth D‒A and long fourth A‒D. Decartes’, and thus Klumpenhouwer’s, problem stems from interpreting “singing in tune in JI” as meaning “use only the ratios in Zarlino’s senario for singing melodic intervals.”
32In deference to the vision of a wholly idealized choir singing the Prologue, the neuter third-person singular pronoun is used to eliminate any hint of gender-based problems due to employment of singers. As a given compositional agent, references to Lasso still use “he.”
33Barbour, Tuning and Temperament, 198‒99.
34Ibid., 196-99; Lindley and Turner-Smith, Mathematical Models, 10n16; Hall, “Quantitative Evaluation.”


